离散变频软启动器的研究

张 臻，吴效威，乔海强，刘 超，刘建鹏，夏远洋

(1.许继电源有限公司，河南 许昌 461000；2.广西大学 电气工程学院，南宁 530004；3.雅砻江流域水电开发有限公司锦屏水力发电厂，四川 西昌 615050；4.广西电力系统最优化与节能技术重点实验室， 南宁 530004)

0 引 言

交流异步电动机因为结构简单、体积小、重量轻、价格便宜、维护方便等特点，在生产和生活中得到了广泛地应用，成为当今传动工程中最常用的动力来源。但是由于其起动特性，电动机直接起动时产生的起动电流通常达到电动机额定电流的5～8倍，甚至更高。过大的电流会造成电动机发热以致会加速电动机的绝缘老化，大大降低电动机的使用寿命，同时全压直接起动产生过高的起动电流将直接影响连接在该电网上的电气设备的运行。为了降低起动电流，电动机起动时通常借助辅助起动装置。随着电力电子技术与现代控制技术的发展，出现了新型的晶闸管软起动装置，现代晶闸管电动机软起动器通常都由微型计算机作为其控制核心，可以方便地满足技术进步的要求，正得到越来越广泛地应用。普通软起动器实质上是通过各种控制策略限制起动定子电流的增加，而初始起动转矩较低的缺点仍不满足对起始转矩要求比较高的应用场合的需求。如何在降低起动电流同时实现电动机的大转矩起动成为了国内外专家所探讨的一个重要话题。本文通过对离散变频控制理论的研究，提出了一种新型离散变频高转矩软起动器控制方案，实现了软起动器起动阶段小电流大转矩的目标，有效地解决了传统软起动器起动初始阶段转矩过小的问题[1]。

1 离散变频原理分析

1.1 离散变频原理

根据电动机的数学模型，如图1所示，采用基于T型等效电路对异步电动机起动时的电压、电流、转矩等变量的关系进行深入研究分析[2]。

图1 异步电动机T型等效电路

由电机学知，三相异步电动机的电磁转矩理论值为

(1)

假定t=t0时刻起动，t=0-1转子转速n=0，转差率s=1，初始起动转矩为

(2)

初始起动电流为

(3)

由上述分析可知，初始起动转矩与电动机定子侧电压的平方成正比例关系，初始起动电流与定子侧电压成正比例关系。即降低电动机起动电压可以减小起动电流，但是缺点是初始起动转矩较小。如何实现在定子电压下降的同时减小输入电压频率则能实现软起动器的较低软起动电流情况下同时大幅提高初始起动转矩。

根据交流调压理论[3]，离散变频理论即在降低输出电压同时使电压频率从一个较低的值开始，通过分级控制频率分级上升，最终达到工频50 Hz。离散变频理论为分级频率控制，使电压的频率分级地变化，各级子频率都是工频的几分之一，即50 Hz的n分频。

采用晶闸管斩波控制方法[4]，在工频50 Hz电压波形的几个半周波形内导通，然后再断开几个周期，等效模拟产生各级频率下的电源波形[5]，如图2所示。

图2 1/2、1/3、1/4分频电压波形示意图

图3 单相12.5Hz→16.7Hz→25Hz→50Hz分频波形示意图

频率由0Hz→12.5Hz→16.7Hz→25Hz→50Hz分级变化，也可在0 Hz和12.5 Hz前面插入更低一级的子频率，例如10 Hz、6.25 Hz等等，见图3。

1.2 最佳相位选择

假定各级子频率系统均为三相对称系统，各相间相位角为120°。若A相的相位角为0 ，B相在A相导通后经过r个半波导通，其新频率下的相位在工频下表示为

(4)

B相在子频率下的相位角应为

(5)

式中,n为自然数，r为大于等于0、且小于2倍n的整数，r的具体取值取决于其相对于另一相相电压波形的晶闸管导通时刻。根据上述分析各级子频率下任意两相之间的相位差可通过下式计算得到。

(6)

若离散变频后各相间的电压相位差α为2π/3，则三相电压相位为三相对称正序电压；当α为 4π/3时，三相电压为对称的负序电压；当α为0时，得到的是零序电压。通过上述分析可知：当n=3m+ 1(m为自然数)，就是为4、7、10、……等一系列数字时，相位差α可能为 2π/3，可以得到正序三相对称电压；当n=3m-1时，就是2、5、8、11……等一系列数字时，相位差α可能是4π/3，可以得到负序的三相电压。

表1 各级子频率相位平衡情况

如表1所示，在某些频率下可以找到正序对称的组合，另外一些频率下仅能找到负序对称的组合，某些频率下则不存在三相对称的组合。若离散变频后各子频率应遵循供电系统中正序分量最大，负序分量最小的原则来选择最优分频及相位组合控制方式，使电动机最大限度的获得正向的电磁转矩[6]。

通过对称分量法对电动机的运行状态进行分析。

(7)

通过对各级子频率下的相位组合进行理论分析，计算各级子频率下各对称分量所占比例，进一步选择各级子频率下的最优离散变频控制方式。利用Matlab中的Simulink建立仿真模型，对各级子频率下各组相位下进行各次谐波幅值分析和转矩计算， 25 Hz、16.7 Hz下的最佳相位组合依次为(0°，210°，150°)、(0°，260°，100°)。

2 离散变频软起动控制策略

采用f1/4→f1/3→f1/2→f1(f1=50 Hz)的起动操作流程，为了保证切换前后各频率的转矩平稳过渡，减小转矩振荡，采用整周期或者半周期切换，或者改进为准整周期或准半周期切换[7-10]。

3 实验验证

3.1 仿真试验结果

根据对离散变频理论的研究与分析，利用Matlab中的Simulink工具，可以建立离散变频起动软起动器的仿真模型[11]，图4所示。

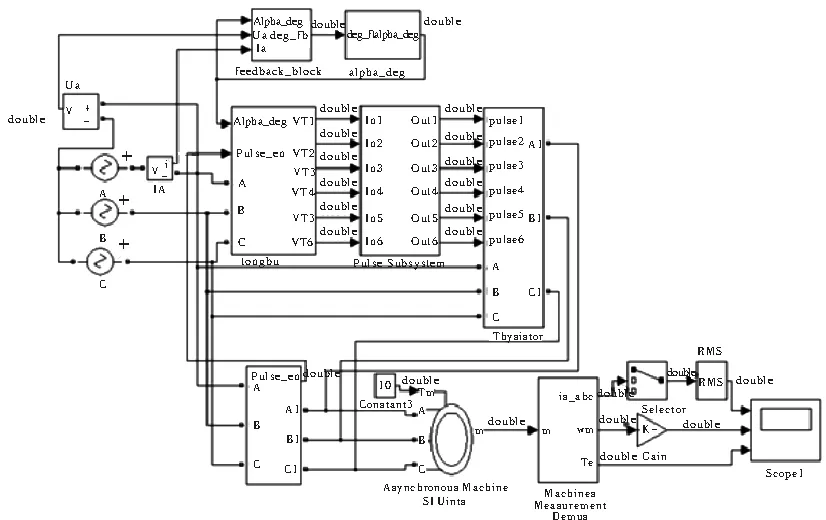
图4 离散变频软起动仿真模型

起动过程仿真波形，见图5。

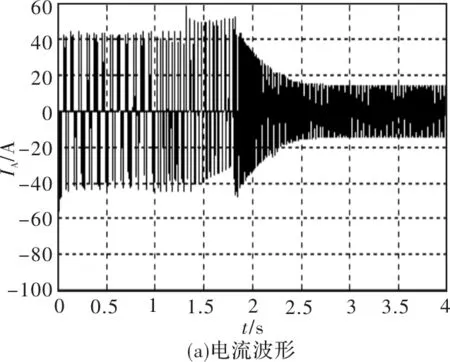
图5 离散变频起动过程仿真波形

普通软起动方式为限流软起动、斜坡电压软起动，通过搭建仿真模型进行仿真，其仿真波形如图6、图7所示。

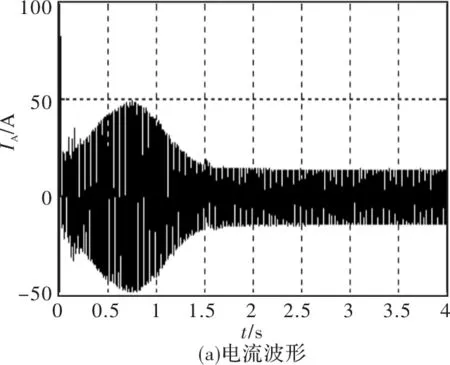
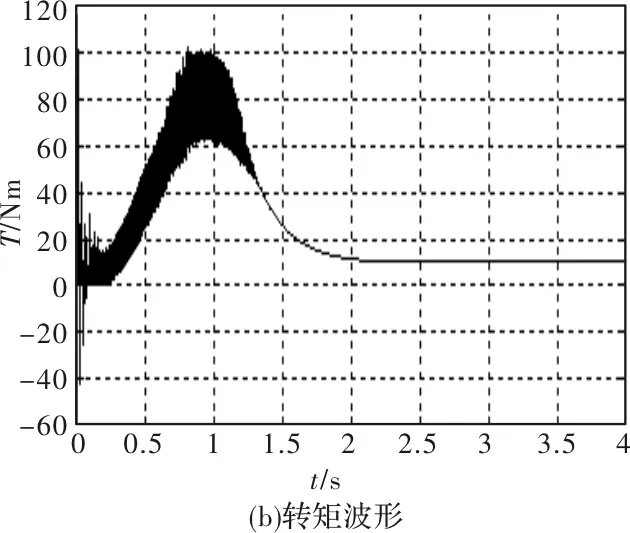
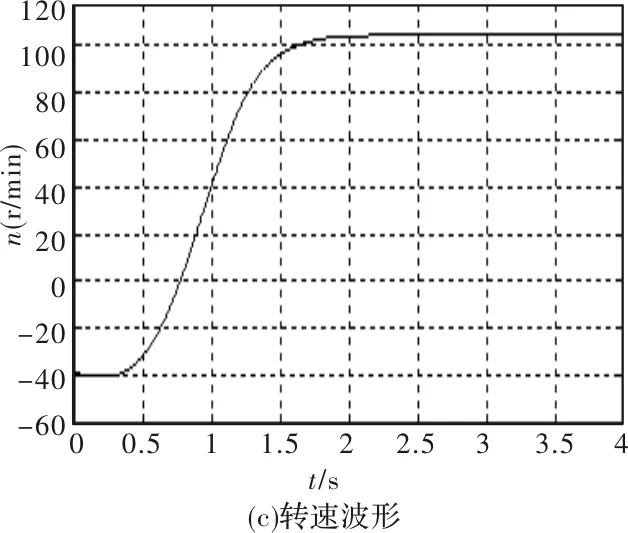
图6 斜坡电压起动过程仿真波形

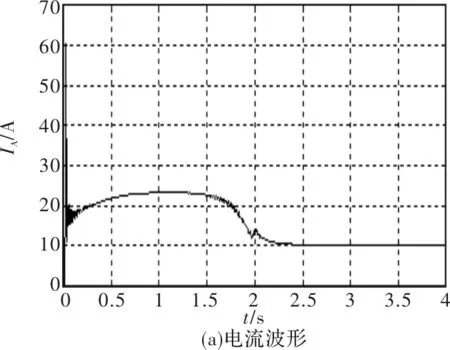
图7 限流起动过程仿真波形

通过上述仿真波形对比可以看出在各种起动方式下，离散变频的起动转矩要比其他传统型软起动方法要大的多，起动电流较小。因此验证了离散变频理论在提高电动机起动转矩方面的理论正确性及有效性。

3.2 试验验证

根据前面的理论研究分析及仿真验证，开发设计了一台离散变频软起动器样机，试验电机为380 V，6.5 kW，额定转速为1400 r/min的三相鼠笼型异步电动机。

离散变频软起动器起动过程电流波形如图8所示，(横坐标坐标为时间轴，每格40 ms；纵坐标为测量值， 1通道每格为20 A，2通道每格为30 A，3通道每格为20 A)。

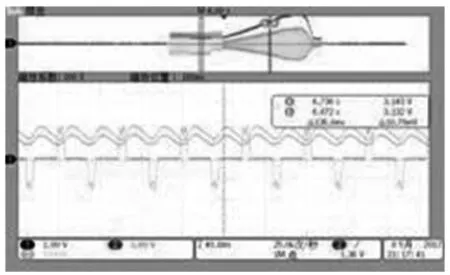
图8 离散变频软起动波形

试验结果表明采用离散变频控制方案下电动机起动电流较小、转矩提升效果明显，满足部分应用场合重载起动需求。

4 结 语

针对普通软起动器初始起动转矩小无法满足重载起动需求，提出了一种基于离散变频控制方法软起动器，试验结果证明了该控制方法的有效性，采用离散变频控制方法的软起动器结构简单，性价比较高，实现降低起动电流同时提高初始起动转矩的功能，满足重载起动应用场合需求，具有重要的实际应用价值。