炸药在密闭容器中爆炸数值模拟和试验

金朋刚，李鸿宾，贾宪振



炸药在密闭容器中爆炸数值模拟和试验

金朋刚，李鸿宾，贾宪振

（西安近代化学研究所，陕西 西安，710065）

为了解炸药在密闭容器中爆炸超压传播规律，测量了TNT在500L密闭容器中爆炸的冲击波超压和准静压，利用AUTODYN建立了二维轴对称模型，获得了冲击波和爆轰产物在容器中的传播过程。研究了传感器附近的凹凸结构对冲击波超压和准静压测试的影响，对比数值计算和实测超压历程曲线。结果表明，数值计算和试验结果基本一致，凹凸结构能够显著影响冲击波超压，而对准静压无影响。

炸药；冲击波超压；准静压；数值模拟；密闭容器；后燃烧

冲击波超压和准静压是评价炸药内爆炸性能的主要参数[1-3]，炸药在有限空间中爆炸产生的冲击波具有多次反射、多峰叠加的基本特点。因此，冲击波传播规律很难预测。目前用于内爆炸冲击波测量的压力传感器主要分为压电式和压阻式两类，但这两种传感器的测量精度受高温及爆轰产物的影响较大，试验人员通常选择多点测量，取有效数据平均值的方法确保测试重复性，试验和数据处理的工作量较大。

数值模拟技术为复现冲击波传播以及爆轰产物飞散过程提供了基础，陈昊等[4]人利用ANSYS LS- DYNA建立了温压炸药在半密闭结构中爆炸的三维数值计算模型，计算了冲击波在结构中的传播过程；曹玉忠等[5]采用计算流体动力学中的二阶精度TVD差分格式和特殊算子分裂法，按轴对称问题，对半球顶圆柱筒密闭式抗爆容器内部爆炸流场进行了数值模拟；辛春亮等[6]人将爆轰产物的后燃烧能引入数值计算模型中，计算得到TNT空中爆炸超压历程曲线，分析了二次压力波的形成过程。但是关于容器内部结构特点对密闭容器中爆炸冲击波和后续压力波影响的研究较少，本文通过建立TNT在500L密闭容器中爆炸的等比例二维数值计算模型，利用AUTODYN自带的炸药爆炸参数计算模型[7]，研究了密闭容器内部小型结构特点对冲击波超压和准静压的影响。

1 试验

1.1 试验布局

密闭爆炸罐整体为回旋体结构，容积约500L。图1为爆炸罐的二分之一剖面图，主要结构有凸台、观察窗、转接块和密封螺帽，传感器安装在转接块上，炸药悬挂于距离凸台170mm的爆炸罐中心位置处，爆心距离两侧的传感器450mm，对于120gTNT炸药，测点处的比例距离为0.91m·kg-1/3。

1.2 试验器材

压装TNT，质量105g，密度1.58g·cm-3，采用10g JH-14传爆药和8号电雷管起爆，装药的TNT当量约为120g。PCB161、PCB162压电式压力传感器各1支，量程6.9MPa，满幅输出5V，采样速率1M/s；适配器F482型ICP传感器专用适配器，PCB公司；波形记录仪：JV-200型波形记录仪。

2 数值模拟

2.1 物理模型

根据实际工况，建立了二维数值计算模型，鉴于爆炸罐为回旋体对称结构，为了提高计算效率，建立了四分之一轴对称模型，取Y轴对称，获得爆炸罐的二分之一剖面，模型容积为500.3L。在炸药的不同方位处设置了9个测点，其中测点3、4、5分别对应于和炸药爆心、下端面和上端面平行的测点，见图2（a）。

爆炸罐壳体厚度为40mm，径向划分4个网格，网格尺寸约1cm，空气介质径向划分200个网格，轴向划分400个网格，网格尺寸大约为2mm，炸药和空气采用欧拉网格，爆炸罐壳体采用拉格朗日网格，两者之间定义ALE流固耦合算法，网格划分见图2（b）。

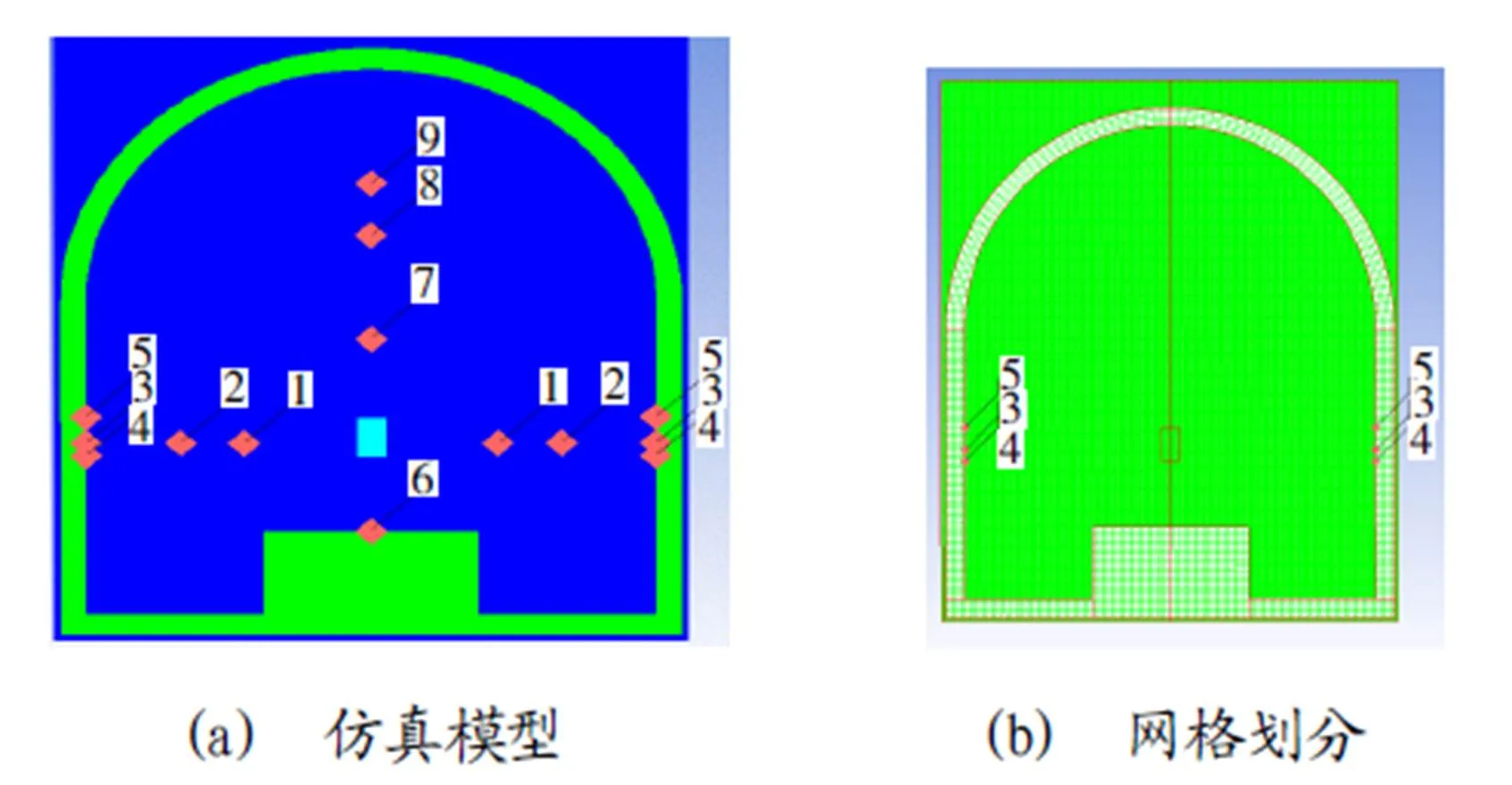
图2 仿真模型及网格划分

2.2 材料模型

TNT炸药的材料模型选择使用AUTODYN自带的材料TNT-2，炸药爆轰产物状态用JWL状态方程描述。材料模型方面，采用JWL状态方程：

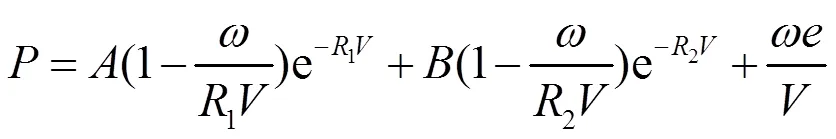
式（1）中：为比内能；为相对比容，=/0，为无量纲量；，，1，2和均为JWL状态方程参数，可以利用圆筒试验进行标定，本文所用JWL状态方程参数列于表1。

表1 JWL装填方程参数

Tab.1 The JWL equation of state of TNT-2

方程（1）中的3项分别在爆炸的高压、中压和低压环境起主导作用，爆炸后期，爆轰产物状态用理想气体状态方程描述，绝热指数取1.3，准静态压力实际上就是冲击波反射、爆炸放热对产物和空气加热效应的综合体现。

空气的状态方程采用理想气体状态方程，即：

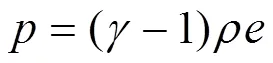
式（2）中：为压力；为绝热指数；为密度；为初始比内能。

爆炸容器的材料为钢，选用STEEL-1006材料模型，采用John-Cook材料模型描述其本构关系，即：

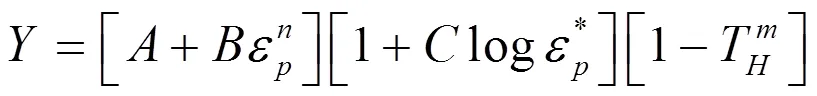
3 试验结果与讨论

进行3发试验，每次采取对称位置处各安置1个传感器，结果取2个传感器所测值的算术平均，见表2。由表2可见，冲击波峰值超压测试结果波动较大，准静压测试结果重复性较好。试验所测典型的超压——时间历程曲线见图3。

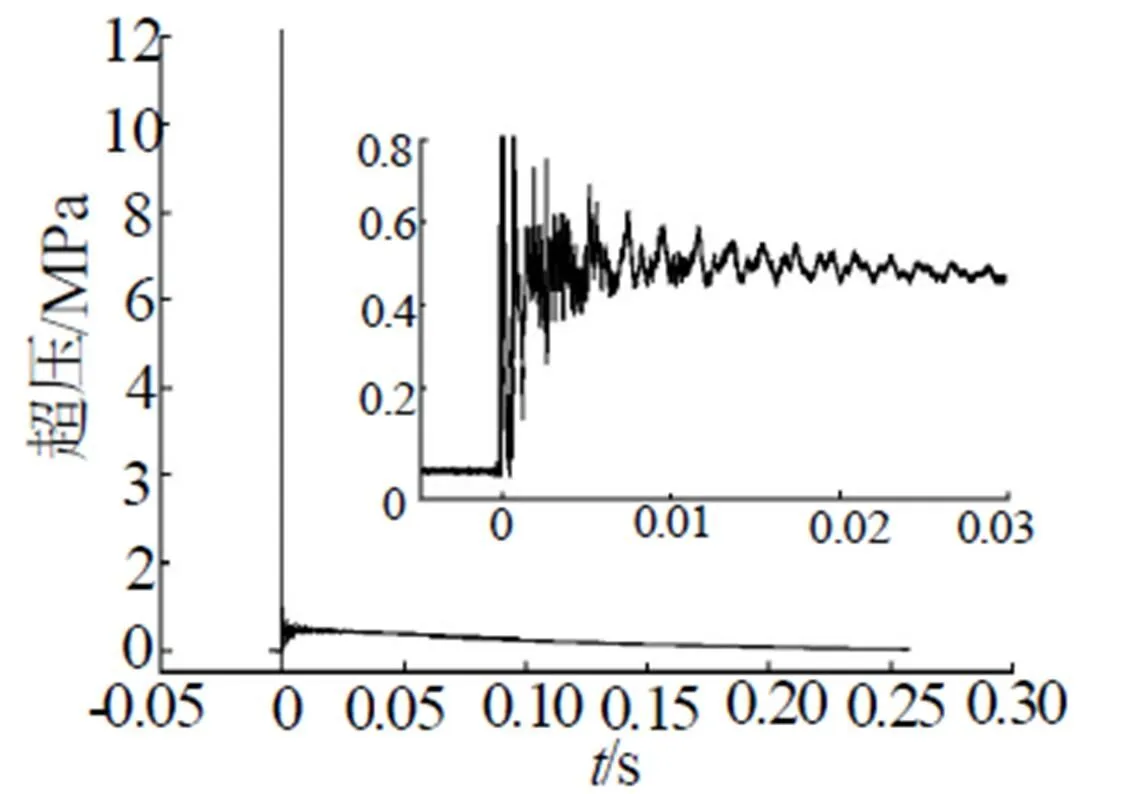
图3 典型的超压——时间历程曲线

由图3可以看出，冲击波到达之后，压力迅速衰减（见右上角的局部放大图）至基线附近，但没有回零，随后压力逐渐回升，5ms之后压力幅值达到准静压附近，由于反射冲击波的影响，初期压力幅值跳动较大，10ms以后爆炸罐内的压力逐渐匀化，处理超压历程曲线得到冲击波峰值超压为14.0MPa，准静压为0.50MPa，数值计算和试验结果列于表2。由表2可见本文所用计算方法能够较为准确地计算冲击波超压和准静压。

表2 试验结果

Tab.2 The test result

试验中，传感器距离爆心450mm，对比距离为0.91m·kg-1/3，根据经验公式计算得到自由场空爆条件下测点处的冲击波超压为1.2MPa，根据反射压力增强2～8倍的基本理论，试验所测冲击波超压应为2.4～9.6MPa，而本试验结果已经远远超过该范围的上限，因此可以推断冲击波在容器内部发生了多次叠加，导致测点处冲击波超压显著增强。

4 数值模拟结果与分析

4.1 冲击波及爆轰产物轨迹演变过程分析

为进一步了解冲击波在容器内部的传播过程，利用AUTODYN对该工况做了仿真计算，图4为TNT爆炸后在爆炸罐内产生的压力及爆轰产物轨迹演变图。

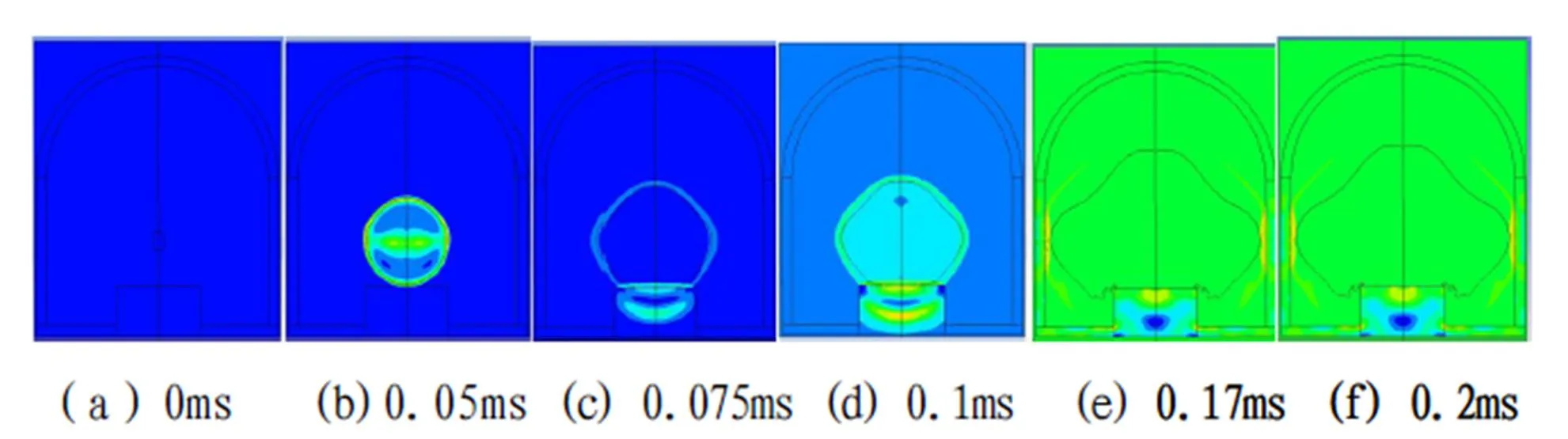
图4 爆炸罐内压力演化图

由图4可见，初期冲击波呈球形传播，各方向的冲击波速度是相同的，起爆0.05ms时刻，冲击波到达凸台，此时冲击波平均速率为3 400m/s；受凸台反射冲击波和初始冲击波叠加的影响，炸药径向冲击波波速迅速增加，使得径向冲击波速度大于轴向冲击波速度，爆炸场内的冲击波传播呈蘑菇状发展；0.17ms时刻，径向冲击波到达爆炸罐侧壁，0.2ms时刻，侧壁冲击波作用位置处的压力急剧增加，此时径向爆轰产物也到达壁面附近。计算可得0.05~0.17ms冲击波平均速率为2 333m/s。

对比测点1、2、3的压力历程曲线，结果见图5。

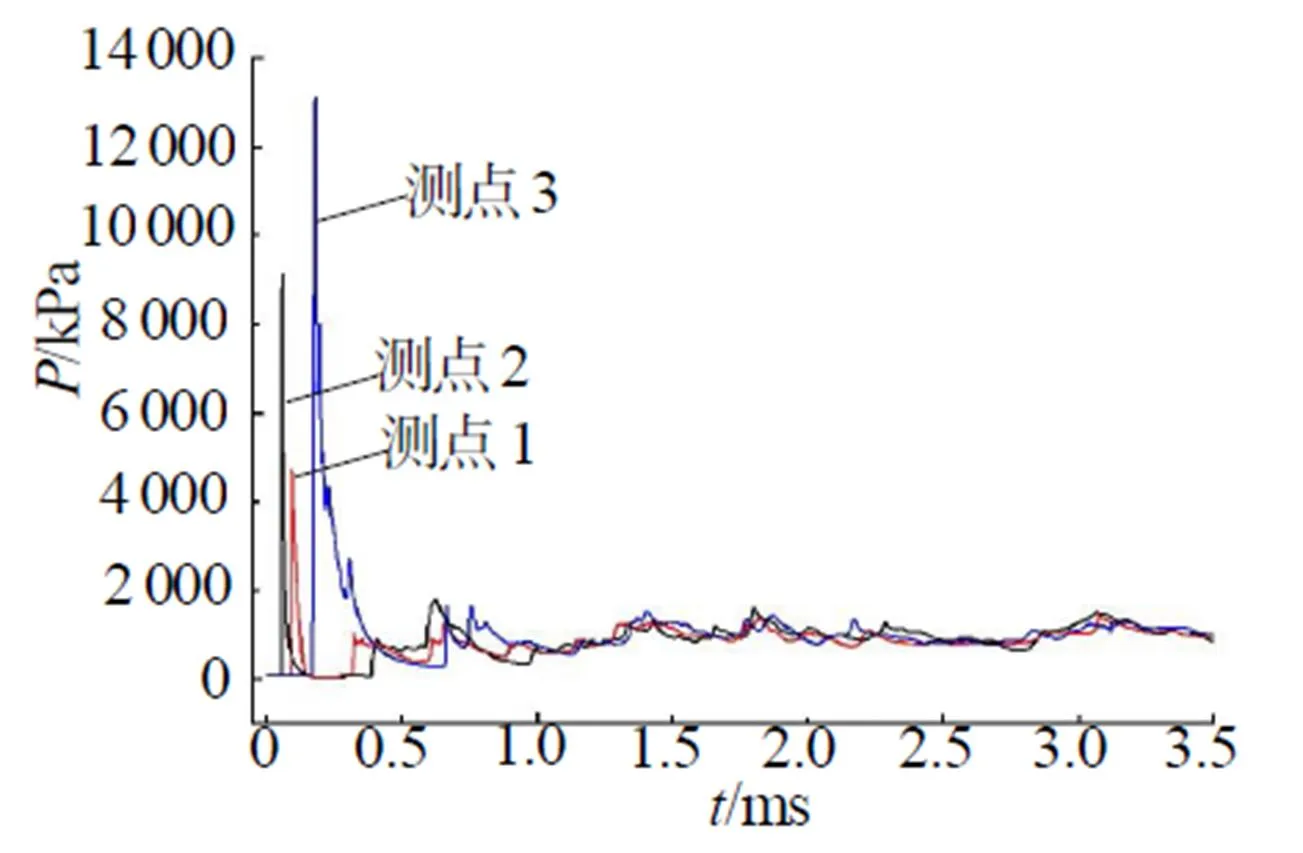
图5 测点1、2、3的压力历程

由图5可见，约0.17ms时刻，冲击波达到测点3，由于凸台反射冲击波的叠加和侧壁的反射作用，冲击波得到大幅度增强，起爆2ms之后3个测点的压力基本一致，说明爆炸罐内部的压力已经匀化，此时容器内部的压力可以用准静压表示。测点3、4、5分别对应于和炸药爆心、下端面和上端面平行的测点，试验过程中由于传感器安装孔的位置不同，测点位置会有略微的差异，为了考察这种差异对冲击波压力测量的影响，将测点3、4、5的压力历程曲线绘制于图6中。

由图6可见，3个测点的冲击波峰值压力和准静压基本一致，读取数据可得冲击波峰值超压和准静压分别为13.0 MPa和0.51MPa，说明本工况下，测点位置的微小变化对于测试结果基本没有影响。

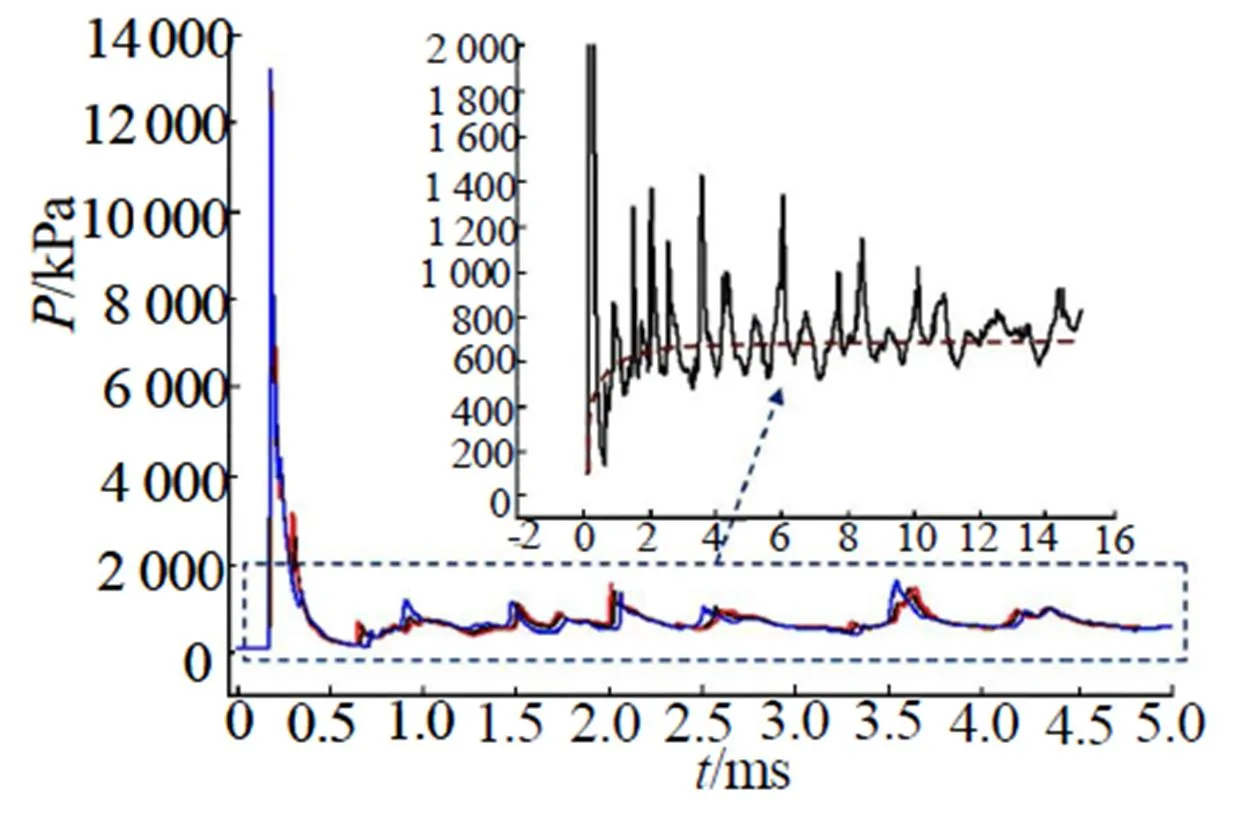
图6 测点3、4、5的压力历程

4.2 局部结构特性对冲击峰值压力和准静压的影响

实际测量中转接块和传感器的对接部分存在约1cm的凸起结构，如图7所示。

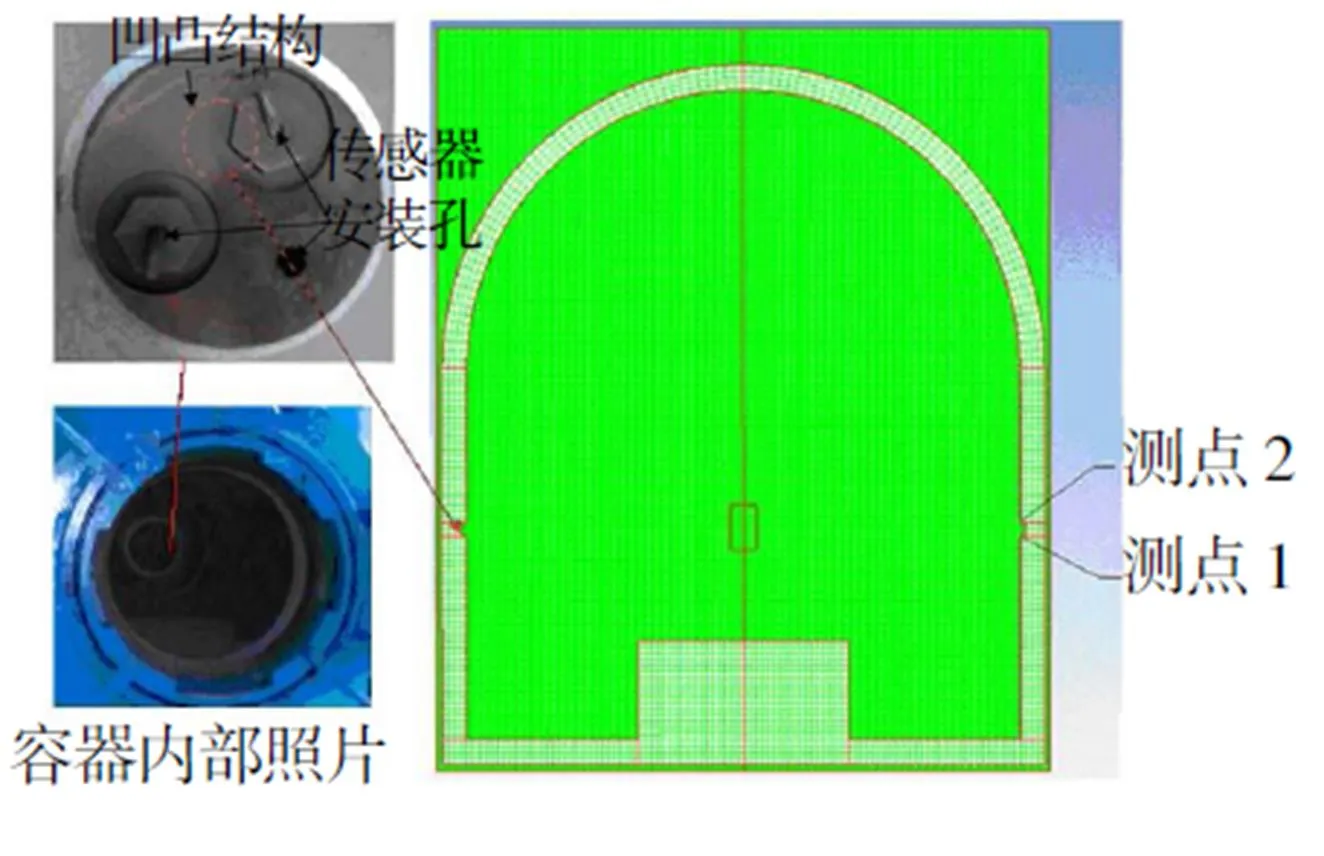
图7 数值计算模型（含1cm凹坑）

为了考察这种微小结构对冲击峰值超压和准静压的影响，利用相同的算法，建立了图7所示的数值计算模型，炸药侧壁正对位置处设置了高2.5cm、深1cm的凹坑，模拟转接块和传感器连接位置处的凹凸结构。测点1和测点2分别对应于结构的上端点和下端点。计算结果如图8所示。

图8 测点1和2的压力历程曲线

由图8可见，测点1和测点2的冲击波超压分别为11.2MPa和9.2MPa，说明凹凸结构对冲击波峰值压力产生了显著影响，而对准静压基本无影响，实际测量中应该对微小结构引起重视，这也可能是导致试验中冲击波超压测试重复性较差的原因之一。

5 结论

（1）内部结构复杂的密闭容器中，炸药爆炸冲击波超压通常难以预估，本试验条件下在对比距离为0.91m·kg-1/3的测点处，冲击波超压达到了14.0MPa的超高值，数值模拟结果表明，这是由于冲击波被炸药底部凸台反射增强，并和侧向初始冲击波发生正向叠加所致；

（2）数值模拟结果表明，传感器附近的微小结构对冲击波超压测试有显著影响，两个相距25mm的测点，冲击波超压相差2.0MPa，这可能是导致冲击波超压测量结果重复性差的原因之一，试验过程中应该引起重视。

[1] 饶国宁,陈网桦,梁德山,等.密闭空间内不同炸药爆源的能量输出结构及与目标作用研究[J].爆炸与冲击,2007,27(5):335- 450.

[2] 李鸿宾,金朋刚,严家佳,等.炸药在密闭空间中爆炸准静压的计算方法[J].火工品,2014(1):45-48.

[3] F.Togashi,J.D.Baum,O.A.Soto.numerical simulation of tnt-al explosives in explosion chamber [C]//Seventh International Conference on Computational Fluid Dynamics (ICCFD7). Hawaii, 2012.

[4] 陈昊,陶钢,蒲元.温压药在有限空间内爆炸冲击波的实验研究及数值模拟[J].火炸药学报,2009,32(5):45-57.

[5] 曹玉忠,卢泽生,管怀安,等.抗爆容器内爆炸流场数值模拟[J].高压物理学报,2001,15(2):127-133.

[6] 辛春亮,徐更光,刘科种,等.考虑后燃烧效应的TNT空气中爆炸的数值模拟[J].含能材料,2008,16(2):160-163.

[7] ANSYS AUTODYN Manuals Version 11.0[M]. ANSYS,2007.

Test and Simulation Research of Explosives Detonation in Confined Chamber

JIN Peng-gang, LI Hong-bin, JIA Xian-zhen

（Xi’an Modern Chemistry Research Institute, Xi’an, 710065）

In order to know the spreading rule of shock wave in confined chamber, the overpressure and quasi-static pressure of TNT explosion in a 500L chamber were tested, the 2D simulation model was built by AUTODYN, meanwhile, the spreading law of shock wave and detonation products in the chamber were obtained. The influence of structure near sensors was considered, the simulation and testing result were compared, which shows that simulation accords with the testing result, accented structure near the sensors influence shock wave seriously, while has no effect on the quasi-static pressure.

Explosives；Shockwave；Quasi-static pressure；Simulation；Confined chamber；Afterburning

1003-1480（2019）02-0031-04

TQ560.72

A

10.3969/j.issn.1003-1480.2019.02.008

2018-10-11

金朋刚（1978 -），男，副研究员，主要从事炸药及装药爆炸与安全特种评估技术。