一种改进的基于深度前馈神经网络的极化码BP译码算法

刘斌 李立欣 李静

【摘  要】近年来高性能和低复杂度的信道译码算法一直是5G移动通信的核心技术之一，深度学习方法因在译码性能方面表现突出已成为研究热点。基于深度神经网络的极化码译码器使用多尺度置信传播算法可以得到较低复杂度和延迟性能，但其译码性能依旧有待提高。在多尺度置信传播译码算法的基础上提出了一种具有多偏移因子的最小和极化码译码算法，通过使用交叉熵损失函数与提出的交叉熵多损失函数对深度神经网络译码器进行训练，生成的深度神经网络译码器可以降低复杂度和时延，显著提高译码性能。

【关键词】深度学习;极化码;置信传播;深度神经网络译码器

中图分类号：TN929.5

文献标志码：A      文章编号：1006-1010（2019）04-0008-07

[Abstract] In recent years， channel decoding algorithm with high performance and low complexity has been one of the core technologies of 5G mobile communications. Deep learning methods have become a research hotspot because of the outstanding performance in decoding performance. The polar code decoder based on deep neural network can obtain better decoding performance by using multi-scale Belief Propagation （BP） algorithm， and have lower complexity and delay， but the decoding performance still needs to be improved. Based on the multi-scale BP decoding algorithm， a minimum sum decoding algorithm with multiple offset factors is proposed in this paper. The deep neural network decoder is trained by cross-entropy loss function and the proposed cross-entropy multi-loss function， respectively. The generated deep neural network decoder can not only reduce the complexity and delay， but also significantly improve the decoding performance.

[Key words] deep learning; polar code; belief propagation; deep neural network decoder

1   引言

根據工信部最新统计数据，截至2018年10月末，中国移动、中国联通以及中国电信三家运营商的移动电话用户总数已经高达15.5亿户，和2017年同时段相比，数据增长了10.7%。这些统计数据清晰地表明：未来移动通信系统将面临巨大的流量需求方面的挑战。移动数据需求的激增给现有的蜂窝网络带来了巨大的负担，这已经引发了对第五代移动通信系统的深入研究。高数据速率需要低译码延迟，然而传统的译码算法由于迭代计算导致其具有很高的复杂度。因此，迫切需要设计一种全新的高速低延迟译码器。最近，深度学习方面的研究[1]因为能够解决此类问题而受到了学者的广泛关注。

极化码作为第一种经过严格证明可以达到香农容量的信道编码方法是信道编码领域的新突破。极化码已经被选为5G控制信道的编码方案[2]。其译码算法主要包括连续消除（Successive Cancelation， SC）算法和置信传播（Belief Propagation， BP）算法。SC算法一直是极化码译码中的研究热点，虽然复杂度低，但长码字下存在吞吐量有限和高延迟的问题。与SC译码算法相比，BP译码算法由于并行处理的特性能实现更高的数据吞吐量和更低的延迟，但也引入了更高的计算复杂度，所以最近提出了最小和近似译码算法和早期终止方案[3]以降低复杂度，然而在有限迭代次数下仍不能实现最大似然译码性能。

学者们开始采用深度学习方法来解决低复杂度和低延迟的信道译码问题。在文献[4]中，通过在Tanner图的边上分配适当的权重来改善译码性能，并使用深度学习技术来获得权重，但是该方法需要大量的乘法运算。文献[5]中作者提出了一种神经偏移最小和算法，其中没有乘法运算、参数数量少且硬件实现也比较容易。文献[6]提出了一种深度神经网络译码器，通过学习大量码字可以实现最大后验译码性能，但是长码字增加了训练的复杂度，所以该方法只局限于短码字的使用。文献[7]中将极性码的编码图分成较小的子块并分别进行训练来获得更好的译码性能，但是这种方法复杂度很高，高吞吐量的硬件实现也很困难。文献[8]中提出了一种多尺度BP译码算法以及适用于任意码长的基于深度学习的极化码译码器。

针对多尺度BP译码算法译码性能有待提高的问题，本文首先提出了具有多偏移因子的最小和译码算法，并将该算法用于深度前馈神经网络架构中。其次，通过对比具有多偏移因子的最小和译码算法和多尺度BP译码算法来证明所提出的算法在性能方面的优势。最后，在提出的神经网络译码结构中，将每次译码迭代得到的输出叠加形成的多损失函数用于训练深度神经网络译码器。

2   研究背景

2.1  深度神经网络

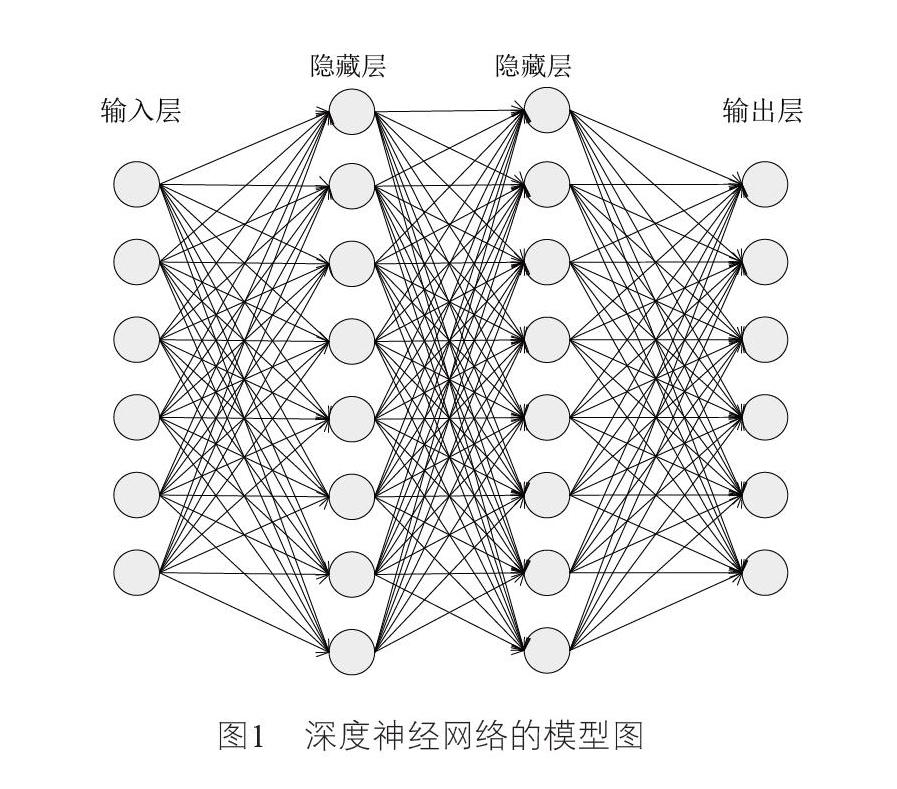
深度神经网络也称作深度前馈神经网络，这种网络模型在各层之间具有全连接的神经元结构，其中信息没有反馈的从左向右传输，图1所示的是深度神经网络的模型。连接输入和输出的每层神经元结构具有以下映射关系：

神经网络中输入和输出映射中的参数通常指的是权重和偏差。前馈神经网络通过多个权重系数矩阵和输入数据在隐藏层中进行一系列线性运算。从输入层开始层层向后传播，最后通过非线性激活函数得到输出结果。为了获得神经网络的最优参数解，输入输出映射的训练集和特定的损失函数必须是已知的。交叉熵损失函数是衡量实际输出值和期望输出值间误差的常用方法之一，通常通过使用随机梯度优化和反向传播算法优化参数以最小化损失函数的值。

2.2  极化码

极化码是Arikan在信道极化研究的基础上提出的一种新的编码思想，当码长趋于无穷时，极化码能够逼近香农极限且具有很低的编码复杂度。极化码的结构基于核矩阵，使用Kronecker乘法线性转换N比特数据，然后通过二进制对称离散无记忆信道传输。极化码生成矩阵的构造方式为：

2.3  BP译码算法

BP译码算法是广泛使用的一种消息传递算法，而极化码BP译码算法是基于Forney提出的码字因子图表示并在因子图上进行的译码。（N， K）极化码的因子图由N（n+1）个节点和n=log2N个阶段组成，每个节点由整数对（i， j）表示，其中i表示阶段，j表示输入比特，并且有1≤i≤n+1，1≤j≤N。图2给出了码长为8的极化码的因子图：

最小和近似译码算法是一种可以降低BP译码算法复杂度的改进算法，硬件上易于实现。其基本思想是将BP译码算法信息更新公式（3）中的g（x， y）简化为g（x，y）=sign（x）sign（y）min（|x|，|y|）。由于使用近似，与原始BP译码算法相比，误比特率（Bit Error Ratio， BER）性能会有一定的降低。为了减少最小和译码算法与BP译码算法之间的性能差距，已经提出了一些解决策略，如偏移最小和译码算法（Offset Min-sum Algorithm， OMSA）、归一化最小和译码算法（Normalized Min-sum Algorithm， NMSA）等[9]。

3   深度神经网络译码器

3.1  具有多偏移因子的最小和译码算法

目前OMSA和NMSA已广泛用于低密度校验（Low Density Parity-Check， LDPC）码的译码中，也可以把这种译码思想应用到极化码中。与最小和近似译码相比，OMSA译码算法性能有很大提升，在中高信噪比区域甚至超过了BP译码算法的性能。与NMSA算法相比，OMSA算法有相对较好的译码性能。对NMSA译码算法中的单一因子α取不同的变量时可以得到具有多个归一化因子的最小和（Multiple Normalized Min-sum， MNMS）译码算法，此时的算法等效为多尺度BP译码算法。

本节中提出了一种具有可学习偏移参数的多偏移最小和（Multiple Offset Min-sum， MOMS）译码算法。与OMSA算法使用单个全局偏移参数不同，MOMS算法中使用多个偏移参数，其中可学习的偏移因子减少了由最小和近似带来的性能损失。MOMS译码算法中消息传递的更新迭代公式为：

与NMSA算法相比，OMSA算法虽然计算复杂度以及译码时延高，但其译码性能突出。所以如果这两种算法在每次译码迭代过程中每个节点处使用不同的参数因子，得到的改进MNMS译码算法和MOMS译码算法性能上都会有所提升，并且MNMS译码算法的译码性能可能会不如MOMS译码算法。也可以说多尺度BP译码算法的译码性能可能不如MOMS译码算法，不过译码性能的比较还是应该通过最后的仿真结果来确定。但可以明显看出MOMS译码算法的复杂度相对较高，所以译码时延也会较高。同多尺度BP译码算法一样，MOMS译码算法中的多个偏移因子通过传统的方法也很难求解，所以后面会根据深度神经网络来帮助求解算法中的多个偏移因子，进而完成极化码的译码过程。

3.2  深度神经网络译码器

传统的信道译码算法中使用的单个参数因子通常是通过仿真实验或者经验获得的，但这并不是最好的求解方法，因为通过实验或者经验并不能得到最优的参数。同时，当使用MNMS译码算法、MOMS译码算法或者多尺度BP译码算法对极化码进行译码时，需要求解的参数数量会大大增加，因此通过传统的仿真实验求解最优参数显然不现实。而深度学习具有处理复杂任务的能力，可以使用该工具去求解上述算法中复杂的参数问题。同时，由于深度前馈神经网络和极化码的BP因子图在结构上相似，所以可以使用深度神经网络来解决信道译码的问题。上一小节提到的MNMS译码算法、MOMS译码算法以及多尺度BP译码算法中的多个参数可以看作是深度前馈神经网络的权重，这些权重可以通过使用小批量随机梯度下降来训练。

更确切地说，本文使用的深度前馈神经网络译码器可以看作极化码BP因子图的展开形式。图3给出了（8， 4）极化码在神经网络中的一次完整的迭代译码过程，它是根据图2所示的（8， 4）极化码的BP因子图展开的。输入层由8个神经元组成，隐藏层对应着从左到右的信息传输和从右到左的信息传输，它们分别占据2层神经网络和3层神经网络，所以中间总共有5层隐藏层。从右到左信息传输的最后一个隐藏层计算原始因子图的最左边节点的输出。为了让神经网络译码器得到的码字估值范围为[0， 1]，最后一层网络的输出层需要使用sigmoid激活函数来处理上一层网络的信息。对于（N， K）极化码，展开极化碼的因子图可以得到每层都包括N个神经元的深度神经网络译码器，它是由输入层、输出层以及中间（2n-1）个隐藏层组成的，其中n=log2N，并且中间的隐藏层分别对应着（n-1）层从左到右的信息传输和n层从右到左的信息传输。

为了增加神经网络译码器的网络深度以及译码迭代次数，可以直接增加分别对应着从左到右的信息传输和从右到左的信息传输的隐藏层的数量，每一次译码迭代后的输出作为下一次迭代的输入。对于（N， K）极化码，通过T次迭代译码后，可以得到总共包含（2（N-1）T+3）层的深度神经网络译码器。图4是经过T次迭代的神经网络译码器结构。

为了评估所使用的神经网络译码器的译码性能，这里采用交叉熵损失函数来衡量深度神经网络实际输出值和期望输出值之间的差距：

其中，N表示码字长度，yi和oi分别表示深度神经网络期望的输出值和实际的输出值。事实上，每次迭代后可以在深度神经网络译码器的结构中添加一个额外的輸出层，并将每次迭代后的输出加到原来的损失函数中生成新的多损失函数。多损失函数通过梯度下降优化方法可以加快梯度更新的过程并向译码器的更深层学习。形成的新的交叉熵多损失函数可表示为：

4   训练及仿真结果

4.1  训练细节

本文使用的深度神经网络译码器模型是在深度学习框架Tensorflow[10]上通过学习率为0.001的Adam[11]梯度下降优化算法进行训练的。为了评估深度神经网络译码器的译码性能，通过蒙特卡罗方法进行仿真实验。选取全零码字作为训练数据，该数据是经过高斯信道传输得到的，信噪比的范围为1 dB～5 dB，选取150个码字作为mini-batch的大小（每个SNR分配30个码字）。测试数据是经过极化编码，二进制相移键控调制并在高斯信道上传输后得到的随机二进制信息。使用标准正态分布中的随机值初始化神经网络的权重。

训练深度神经网络译码器时，网络深度是影响译码性能的一个重要因素，通常网络层数越多得到的译码性能越好，但是会产生很高的训练复杂度，所以应该选择合适的网络深度来获得BER性能和计算复杂度之间的一个折中。这里使用贪婪搜索算法来衡量神经网络的深度大小：

（1）首先对于（N， K）极化码，通过一次迭代译码后，得到的深度神经网络译码器的层数为（2（N-1）+3）。

（2）上面的神经网络经过训练并达到收敛后，再将测试数据输入到已经训练好的神经网络中来获得BER性能。

（3）增加步骤（1）中的译码迭代次数，每增加一次迭代，神经网络的层数增加（2n-1）层，并重复步骤（2）直到BER性能曲线趋于平稳。

4.2  仿真结果

这一部分给出了深度前馈神经网络译码器对（64， 32）和（512， 256）极化码进行译码的结果，并对比了MOMS译码算法和多尺度BP译码算法的BER性能差异。

对于（64， 32）极化码，通过上面的贪婪搜索算法测试了网络深度（或者迭代次数）对BER性能的影响，结果如图6所示。从图6可以看出，一次迭代的效果非常差，并且随着迭代次数增加译码性能变得越来越好，最后在迭代次数为5的情况下BER性能曲线相对稳定。所以选择T=5作为理想的迭代次数，此时深度神经网络译码器总共包括53层。基于这个结果，图7展示了（64， 32）极化码的深度神经译码器在5次迭代下进行训练的收敛情况，图7中的1个epoch指的是将训练集中的全部样本训练一次，仿真结果中BER性能在6个epoch左右保持稳定，这表明了训练的收敛性。

实验也对比了多尺度BP译码算法（MSBP）和具有多偏移因子的最小和译码算法（MOMS）对（64， 32）和（512， 256）极化码进行译码的BER性能，考虑到训练的复杂度以及算法的可对比性，神经网络译码器都选择T=5作为迭代次数，并分别在图8中给出了仿真结果。两种算法在低信噪比情况下虽然性能相当，但是与多尺度BP译码算法相比，可以看出所提出的具有多偏移因子的最小和译码算法具有一定的性能提升，并且在相同码长下的高信噪比区域具有更好的译码性能。当然该算法对（512， 256）极化码进行译码能得到更好的BER性能，显然可以得出网络越深译码性能越好的结论。这些结果验证了具有多偏移因子的最小和译码算法优于多尺度BP译码算法。同时图9给出了（512， 256）极化码用多损失函数训练得到的BER译码结果，从图9可以看出用多损失函数训练的译码算法有更低的比特误码率，在高信噪比区域内能实现高达0.7 dB的性能改善。

5   结束语

本文提出了一种多偏移最小和译码算法，该算法通过使用多个可学习的偏移参数来推广偏移最小和译码算法，可以应用于极化码的深度神经网络译码结构中。通过仿真结果可以看出，与多尺度BP译码算法相比，本文提出的多偏移最小和译码算法可以获得更好的纠错性能，同时通过训练具有多损失函数的深度神经网络可以获得较低的BER性能，为今后进一步设计极化码译码器提出了新的解决方案。

参考文献：

[1] Goodfellow I， Bengio Y， Courville A， et al. Deep learning[M]. Cambridge： MIT press， 2016.

[2] Polar码成为5G新的控制信道编码[J]. 上海信息化， 2016（12）： 87-88.

[3] Pamuk A. An FPGA implementation architecture for decoding of polar codes[C]//2011 8th International Symposium on Wireless Communication Systems.Aachen， Germany， 2011： 437-441.

[4] Nachmani E， Beery Y， Burshtein D. Learning to decode linear codes using deep learning[C]//2016 54th Annual Allerton Conference on Communication， Control and Computing. Monticello， IL， 2016： 341-346.

[5] Lugosch L， Gross W J. Neural offset min-sum decoding[C]//2017 IEEE International Symposium on Information Theory （ISIT）. Aachen， Germany， 2017： 1361-1365.

[6] Gruber T， Cammerer S， Hoydis J， et al. On deep learning based channel decoding[C]//2017 51st Annual Conference on Information Sciences and Systems. Baltimore， MD， 2017： 1-6.

[7] Cammerer S， Gruber T， Hoydis J， et al. Scaling deep learning-based decoding of polar codes via partitioning[C]//2017 IEEE Global Communications Conference. Singapore， 2017： 1-6.

[8] Xu W， Wu Z， Ueng Y L， et al. Improved polar decoder based on deep learning[C]//2017 IEEE International Workshop on Signal Processing Systems. Lorient， France， 2017： 1-6.

[9] Angarita F， Valls J， Almenar V， et al. Reduced-complexity min-sum algorithm for decoding LDPC codes with low error-floor[J]. IEEE Transactions on Circuits and Systems I： Regular Papers， 2014，61（7）： 2150-2158.

[10] Abadi M， Agarwal A， Barham P， et al. Tensorflow： Large-scale machine learning on heterogeneous distributed systems[Z]. 2016.

[11] Kingma D P， Ba J. Adam： A method for stochastic optimization[Z]. 2014.