以“三角形的中位线”为例谈初中数学课堂导入策略

胡利清

摘要：课堂导入是课堂教学必不可少的重要环节，它能安稳学习情绪，吸引学生注意，激发学习兴趣，沟通师生感情等。一堂课导入的成与败直接影响整堂课的效果，本文从五个方面对“三角形的中位线”进行不同层面的导入，并进行比较研究，阐述教师要根据学生实际出发，紧扣教学目标和教学内容，着眼于学生对所学内容的理解、巩固、完善和提升，择优导入。

关键词：课堂导入;三角形;中位线;学习兴趣

中图分类号：G633.6   文献标识码：A   文章编号：1992-7711（2019）01-0005

新一轮的课程改革已经进入了全面实施的阶段，新知识导入的教学越来越引起了广大教师的关注。苏霍姆林斯基说：“如果老师不想办法使学生产生情绪高昂的智力振奋的内心状态，就急于传授知识，那么这种知识只能使人产生冷漠的态度，而给不动感情的脑力劳动带来疲劳。”实践证明，积极的思维活动是课堂教学成功的关键，而富有启发性的导入可以激发学生的思维兴趣，所以教师上课伊始就应当注意通过精彩的导入来激发学生的思维，以引起学生对新知识新内容的热烈探求。课堂导入是课堂教学的主要环节之一，一堂课导入的成与败直接影响着整堂课的效果。本文通过对新浙教版教材中八下数学“4.5三角形的中位线”的课堂导入进行研究，进一步探讨初中数学课堂导入设计的方法和途径。

一、实例探求法导入

实例探求法导入是利用现实生活中的具体实例分析和揭示事物的一般规律，是探求知识的一个重要途径，也是引入课题的一种方法。

实例的选用应当充分考虑学生的认知水平和活动经验，应当在反映数学本质的前提下尽可能贴近学生的现实，以利于他们经历从现实情境中抽象出数学知识与方法的过程。

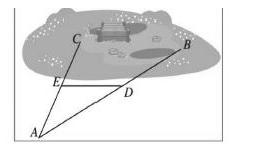
例如，在讲解“三角形中位线定理”时，可先引入以下实例：为了测量一个池塘的宽度BC，小明在池外取一点A，连结AB、AC，及其中点D、E，量得DE的长度，便得到这个池塘的宽度。

这个问题的提出，自然会引起学生的好奇心，激发学生探求知识的欲望。

实例的导入容易激发学生学习数学的兴趣，使他们感受到数学就在自己身边，也易于他们理解相关数学知识，体会到数学的作用。

二、复习导入

复习导入法是指在讲授新课时，首先复习以前所学的知识，并在此基础上提出问题，这样既可以使旧知识得以巩固，又能调动学生进一步学习的积极性。数学是一门系统性很强的学科，如果前期基础打不牢，必然影响后续课程的学习。因此在新课导入时可以用旧知识进行铺垫，不但能起到“温故而知新”的作用，而且学习起来没有陌生感。

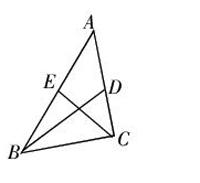
如图：（1）BD，CE分别是△ABC中边AC，AB上的中线，

已知AC=6，BE=4，则AD=    ，AB=    。

（2）连结DE，并思考：这和我们的三角形中线一样吗？

若不一样，那我们给它取个什么名字好呢？

（3）若DE=3，你能猜测出BC的長吗？

先从三角形的中线着手，回顾一下三角形中线的定义和结论，然后通过设问自然地引出三角形的中位线概念，并能顺理成章地了解三角形的中位线和中线之间的联系与区别，为下面习题的讲解作铺垫。

复习导入法在常规课中经常会被用到，根据奥苏泊尔的同化理论，任何一个新知识均可以通过上位概念、下位概念和先行组织者，寻找它与旧知识的联系作为新概念的增长点，促进新知识的学习，还能够更好地揭示相关数学知识之间的内在联系，有利于学生从整体上理解数学，构建数学认知结构。

三、精心设疑法导入

美国心理学家布鲁纳说：“教学过程是一种提出问题和解决问题的持续不断的活动。”思维永远是从问题开始的。教师可以在教学开始，根据学生的认知水平，提出形式多样、富有启发性的问题，引导学生回忆、联想、预测，或渗透本课学习的主题，从而调动学生的学习积极性。

问题：你能将任意一个三角形分成四个全等的三角形吗？

这四个全等的三角形能拼成一个平行四边形吗？（用多媒体展示）

（提示：可以通过猜测、实验、验证等手段来回答本小题。）

这一问激发了学生的学习兴趣，学生积极主动地加入到课堂教学中，课堂气氛变得较为和谐，课堂也鲜活起来了。

你有办法验证吗？

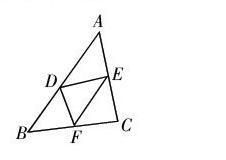
生1：（如图1）沿DE，DF，EF将画在纸上的△ABC剪开，看四个三角形能否重合。

生2：分别测量4个三角形的三边长度，判断是否可利用“SSS”来判定三角形全等。

生3：分别测量4个三角形对应边的边及角，判断是否可利用“SAS，ASA或AAS”来判定全等。

师：同学们都采用了实验法，存在误差，那么如何利用推理论证的方法验证呢？

问题是教学的心脏，是教学思维的动力，且是思维的方向，数学思维的过程也就是不断提出问题和解决问题的过程。因此，在数学课堂学习中，教师要不断向学生提出新的数学问题，为更深入的数学思维活动提供动力和方向，使数学思维活动持续不断的向前发展。

四、动作操作法导入

布鲁纳的认知发展过程理论认为，学习不是被动地形成刺激反映的联结，而是主动形成认知的过程。学习的主要目的不是要记住教师和教科书所讲的内容，而是要学生参与建立该学科知识体系的过程。学生不是被动、消极的知识接受者，而是主动、积极的探究者。在学生主动形成认知的过程中，他主张采用“发现学习”的模式。实践活动是兴趣形成与发展的重要因素，有关几何知识的教材，采用动手操作导入新课的方法效果良好。

动手操作：（1）请同学们在纸上任意画一个△ABC;（2）分别取AB，AC的中点D，E，连结DE。

见证奇迹的时刻到了……

“你只要告诉教师图中任意的两个角的度数，教师便能知道图中所有角的度数。你只要告诉教师线段DE的长度，教师便能告诉你边BC的长度。你们信不信？谁想试一试？你们想不想知道其中的秘密呢？”

通过学生的动手操作，学生能很好地理解“三角形的中位线”概念，并能快速地猜测出三角形的中位线定理的内容。动手操作导入有助于学生将抽象几何知识直观化，有助于学生发现学习，有助于发展学生的空间观念，有助于学生数学思考和解决问题能力的提高。

五、情境创设法导入

有些概念、性质等基础知识比较抽象，不易理解。通过教师创设的情境，可使学生产生强烈的感情认识。这样导入新课，不仅为学生学习新知扫清了障碍，而且激起了学生探求新知的热情。

师1：多媒体展示右图，观察思考：

（1）图中的所有三角形有什么共同特征？

（2）这个图是怎样画出来的？

师2：教师给出三角形的中位线的概念：连接三角形两边中点的线段叫做三角形的中位线。

师3：为什么作三角形的中位线就能画出这样美丽的图案？三角形的中位线有什么性质？

通过欣赏美丽的图片，创设情境，引起学生强烈的求知欲——想弄明白这样美丽的图片和三角形的中位线之间到底存在着怎样的联系？

数学课堂教学中创设恰当的问题情境，能唤醒学生强烈的求知欲望，保持持久的学习热情，可以培养学生探索知识能力和方法，促进学生全面地获得数学知识。我们在数学教学过程中，可以创设必要的问题情境，极大地激发学生的学习兴趣，提高课堂教学效果。

高尔基曾说：“最难的是开始，就是第一句话，如同音乐上一样，全曲的音调都是它给予的，平常得好好去寻找它。”由导入所奠定的基调将直接显示：①内容的定旨。概括展示全讲内容，让学生明确目的要求，宛如一首乐曲的前奏，让学生把握基本旋律。②情感的基调。让学生初步接触情绪感染，为全身心的情感投出作出准备和酝酿。③语调的定格。导入能确立全课的基本语调，讲述是解说还是抒情，是奋进还是纤弱，是辩驳还是说明，是绚丽还是朴素，以怎样的基调为全课定音，语调也有个总体模式。只有实现了内容定旨、情感定调、语调定格，开场白才算充分发挥了效力，整个课堂教学才井然有序，有条不紊。

以上是本文对“三角形的中位线”这一节课课堂教学导入的五种不同方式，当然，新课导入的方法很多，除上述方法外，还有激情导入法、图示导入法、直接导入法等。在教学中注意创设新颖的开场，有助于激发学生积极良好的學习情绪，促使学生带着一种自觉自愿的心理走进教学内容，去学习、去探索，从而实现学习目标，达到事半功倍的教学效果。新课导入中也有些许需要注意的地方，如这些导入的环节，并不是死板的模式，可以灵活多变地加以应用。采取哪种导入方式最合理？笔者认为，结合学生特点、教学内容相匹配的导入最合理。导入方式的选择必须从教学内容和学生实际出发，紧扣教学目标和教学内容，要着眼于学生对所学内容的理解、巩固、完善和提升。因此，导入方式的选择要因学而异，因课而异，学之有法，导入无定法，妙在巧用中。另外，导入应注意时间的控制，课堂导入时间通常为3-5分钟。课堂导入就好比一节课的敲门砖，用时不宜过长，要为后续重点难点的突破留有足够的时间。

参考文献：

[1] 教育部.义务教育数学课程标准[M].北京：北京师范大学出版社，2011.

[2] 李海东.中小学数学[M].北京：北京报刊发行局，2013.

[3] 王小伶.激发学生兴趣 优化数学课堂教学[J].教育教学论坛，2010（16）.

（作者单位：浙江省桐乡市洲泉中学 314500）