基于规模法则的城市规模与交通拥堵关系研究

伍速锋，吴克寒，王 芮，徐天东

(1.中国城市规划设计研究院，北京 100037；2.上海海事大学，上海 201306；3.佛罗里达大学，美国佛罗里达州盖恩斯维尔 32611-5706)

随着城镇化的不断推进，交通拥堵成为主要的城市病之一，限制大城市规模成为缓解城市交通病的手段之一。然而，这一手段引起了广泛争议。文献[1]提出，通过限制城市规模来缓解拥堵用处不大。但也有一些研究表明，交通拥堵和城市规模之间存在正相关关系。文献[2-3]通过中国的实证分析表明，人口越多的大城市，交通系统的压力也越大，人口对交通拥堵越具有正向作用。汤姆逊(J M Thomson)在《城市布局与交通规划》一书中指出，城市规模对于交通拥堵有重要影响[4]。但该研究侧重于实证，缺乏理论研究。本文利用规模法则并结合实证，从理论的角度研究城市规模与交通拥堵的关系。

1 规模法则

1638年伽利略就在《关于两门新科学的对话》中提出了如下观点：世间万事万物，通常都不能按照简单的线性比例放大。美国物理学家杰弗里·韦斯特(Geoffrey West)从理论和实证上证明了该观点，并在其著作《规模：复杂世界的简单法则》中提出“规模法则”(scaling laws，也被译为“标度律”)的概念[5]。物理学家们进行了进一步的研究，并引入标度律公式研究规模法则，即Y=cXk，考虑到c 为常数，还可以简化为Y∝Xk。研究表明作为幂率的k非常重要，甚至可以决定整个系统的性质[5-6]。如果k=1，即为线性关系，即X增大一倍，Y也增大一倍；如果k＞1，即为超线性关系(superlinear)；如果k＜1，即为次线性关系(sublinear)。

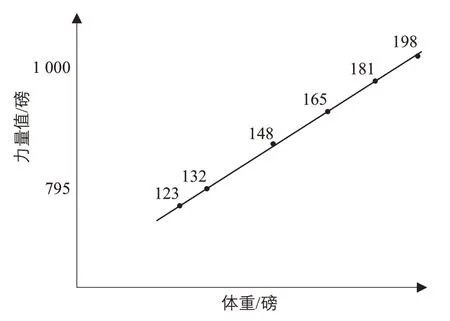
图1 举重运动员体重与力量值Fig.1 Value of the weightlifter's weight and strength

图2 中国城市城区人口和道路长度的关系Fig.2 Relationship between urban area population and road length in Chinese cities

生物体的力量和重量之间是次线性关系。因为力量跟面积成正比，而重量跟体积成正比。由几何学知识可知，面积跟长度的平方成正比，如圆的面积S=πr2。体积跟长度的立方成正比， 如球的体积V=4/3πr3。以圆球形为例，按照物理学上密度均匀的物质，重量跟体积成正比，进而可以推导出：面积(即力量)与体积(即重量)的2/3次方成正比，即S=π(3/4π)2/3V2/3。

化学家利兹克(M H Lietzke)用1956年奥运会举重比赛成绩验证了伽利略提出的观点[4-5]。对Y=cXk两边取对数，得到LogY=Logc+kLogX。若X为体重、Y为成绩，将体重和成绩在坐标系中表示出来(见图1)，其基本为一条直线，斜率为0.675，接近理论值2/3≈0.667。上述原理同样也适用于城市的相关研究。

2 城市规模越大越经济

运输领域存在船越大越经济的规律，其背后主要是规模法则在发挥作用。英国工程师布鲁内尔(I K Brunel)意识到，船的载货能力由体积决定，跟船的尺寸的立方成正比；船在水面上受到水的拖拽力则与船底的面积成正比。因此，船要克服的航行阻力与船的载重量的2/3 次方成正比，是一个次线性关系。如果需要把载重量扩大到10 倍，需要的动力达到原来的4.6倍即可[5-6]。

与船越大越经济相似，城市规模也是越大越经济。韦斯特分析了法国、德国、荷兰和西班牙多个城市的人口数量和加油站个数之间的关系。人口越多，加油站越多，但是加油站的增长比人口慢，加油站数量和人口的0.85次方成正比。因此这是一个次线性关系，意味着城市规模越大(人口越多)，人均所需要的加油站数量就越少[5-6]。

文献[5]揭示了更多的研究成果，城市的道路总长度、水电和煤气管道总长度也与人口的0.85 次方成正比，即城市基础设施∝人口0.85。这个规律意味着大城市比小城市更节省基础设施。本文分析了中国600 余个城市城区人口和道路长度的关系，幂率为0.87，与国外的统计结果比较接近(见图2)。

3 城市规模越大越拥堵

前文提到城市基础设施长度与人口的0.85次方成正比，两侧除以人口数，则城市基础设施/人口∝人口-0.15，即城市人口数越大，人均的城市基础设施数量越少，换言之城市规模越大，设施利用率越高。就交通而言，当这种增长超过交通承载力后，就会导致交通拥堵，国内外城市交通拥堵也基本符合这一机理。

3.1 实证分析

本文选取百度公司2018年第二季度的交通拥堵排名数据作为参考(见表1)，拥堵靠前的多为规模较大的城市[7]。英国主要城市人均高峰拥堵耗时总体上呈现与人口规模正相关的关系(见图3a)。美国主要都市区人均高峰拥堵耗时总体上也呈现与人口规模正相关的关系(见图3b)。其中纽约、芝加哥因为发达的公共交通系统，拥堵有所缓解，纽约的公共交通客运量占全美公共交通客运量的比例超过1/3。

3.2 机理分析

为什么会存在城市基础设施和人口的次线性关系呢？路易斯·贝当谷(Luís M.A.Bettencourt)[8]和卡洛斯·达甘索(Carlos Daganzo)[9]分别做出了数学推理和理论解析。本文利用规模法则的基本理论做出了简化的分析模型。

1）贝当谷的数学推理。

关于0.85 的来历，美国圣塔菲研究所(Santa Fe Institute)的贝当谷做出了数学推理，认为应该接近5/6[8]。推理过程如下。

城市里每个人的基础收益与城市人口密度成正比。设定N代表城市总人口，A代表城市面积，那么人口密度n=N/A。

人均成本与A的1/2 次方成正比，人均基础收益与N/A成正比，而要想让城市维持下去，就要求成本等于基础收益，因此A的1/2次方与N/A成正比，即A∝N2/3。理想城市的面积与人口总数的2/3 次方成正比。这说明越大的城市越拥挤，当然从另一方面也可以说越大的城市越节省土地。

最后，再看基础设施。城市里两个人之间的平均距离d应该等于人均面积的平方根，即。如果这个城市的基础设施好，人均拥有的道路长度应该就是两个人之间的平均距离。即城市道路的总长度Nd应该与成正比。考虑到A与N的 2/3 次方成正比，即。其中，5/6=0.833，这就是前述基础设施幂率0.85的由来。

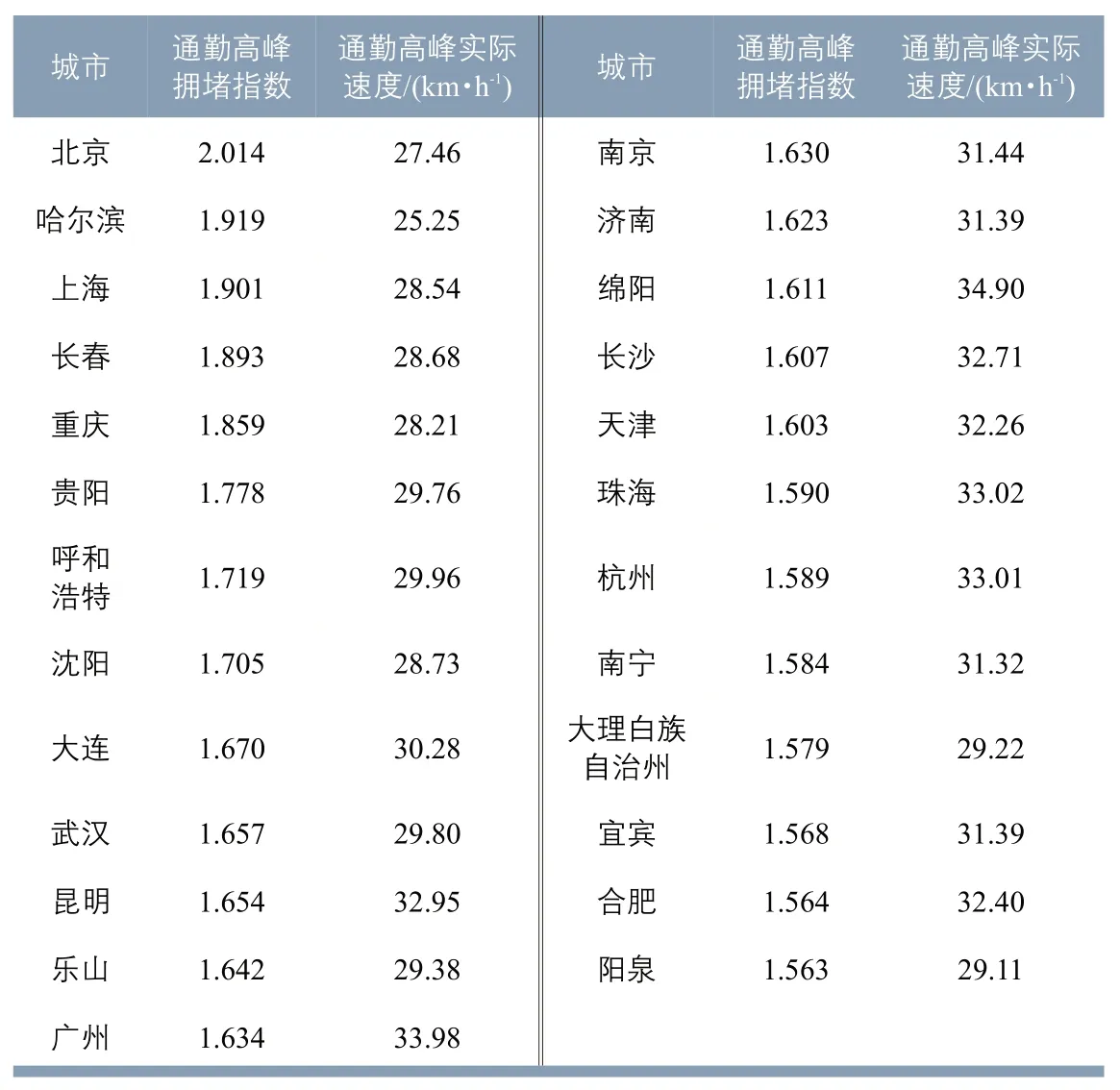
表1 百度公司2018年第二季度的交通拥堵排名Tab.1 Congestion rank of the 2nd quarter released by the Baidu Inc.

图3 英国和美国拥堵排行与人口规模对比Fig.3 Congestion rank and the population in U.K.and the U.S.

图4 城市供需矛盾的本质：规模困境Fig.4 Nature of the contradiction between supply and demand:the scale dilemma

图5 考虑时间因素的规模困境Fig.5 Scale dilemma considering time indicator

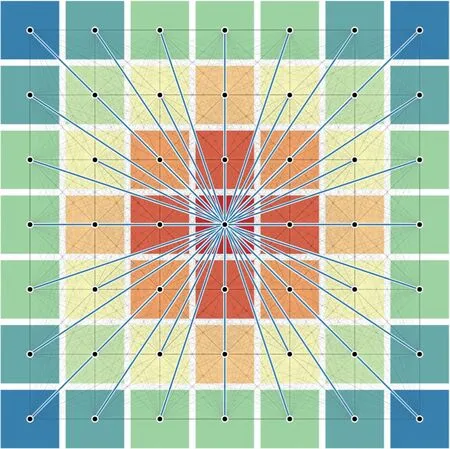
图6 不同规模城市中心对外出行量对比Fig.6 Travel demand between city centers and outside groups in cities with different scales

2）达甘索的理论解析。

2018年10月，美国工程院院士达甘索在一次演讲中[9]做过一个比较通俗的解释。假设一个城市有一个中央商务区(Central Business District,CBD)，CBD 交通的需求量与其面积成正比，CBD边界上能驶入的车辆数与周长成正比，前者是边长的2 次方，后者是边长的1 次方。当边长越大，也就是CBD的规模越大时，交通需求与交通供给之间的矛盾也就越突出(见图4)。

如果考虑时间累积的影响，这个矛盾还会进一步加剧。由于城市街道可容纳的出行量与城市面积成正比，而需要共存的出行量与城市面积和直径的乘积成正比，因此，城市规模越大交通高峰相对呈现越集中的态势(见图5)。大城市的交通高峰持续时间一般长于小城市就是这一规律的体现。

3）简化分析模型。

以标准栅格小区构成的城市为例，假设城市由m×m个栅格小区构成(m为奇数，见图6)，每个栅格小区均向其他小区产生等量出行量T，则中央小区的对外出行量为可见该出行量与城市尺度呈二次方关系，是一种超线性关系。以5×5栅格城市和7×7 栅格城市为例，城市尺度增大1.4 倍，但中央小区对外出行量扩大了2倍。

由城市中央小区对外出行量与城市尺度的函数曲线可见，城市尺度越大，单位尺度增长引起的对外出行量增长量越大，远高于城市面积增长的速度(见图7)。故大城市扩张引起的额外出行量强度高于小城市。

4 城市规模越大产出越高

上述分析表明，城市越大交通倾向于越堵，那么就应该控制大城市的发展吗？对规模法则的研究表明这也是不对的，因为城市的产出和规模是超线性关系，即城市规模越大产出越高[4-5]。

4.1 实证研究

韦斯特利用美国各个城市的经济总量、专业人才数量、专利数量与人口的关系进行分析，发现各项指标与城市规模也符合规模法则(见图8)，幂率约为1.15，即城市产出=人口1.15，反映出超线性关系，意味着城市产出的增长比城市规模的扩张快。对比1 000 万人口的大都市和10 万人口的小城市，人口规模扩大了100 倍。由于100 的0.85 次 方 等 于 50， 100 的 1.15 次 方 等 于200，这两个幂率就表示：城市人口规模扩大100倍，基础设施只需要扩大50倍，而城市的产出却扩大了200 倍。从投入产出比的角度可以说城市越大越好。

文献[10-11]也表明，中国城市人口集聚带来的经济增长率符合规模法则，而且与美国城市相比，幂率系数更高。市辖区人口每增加一倍，经济规模可增加122%(见图9)，这一数字在美国是111%。

4.2 机理分析

为何城市产出和人口是一个超线性关系？因为城市产出源自人与人之间的连接。产出不是由人数决定的，而是由连接数决定的。n个人间两两相连的连接数D和n呈二次方关系。如5个人之间总共有10个连接；而6个人之间总共有15个连接。连接数的增长大大快于人数的增长(当然，城市内人与人之间的实际连接总量因为受各种约束，还达不到二次方关系，但是属于超线性关系)。与此同时，人口密度越大，每个人所能轻易达到的连接就越多，城市总连接就会更多。

5 城市规模与交通拥堵关系的启示

1）城市规模应与交通承载力相协调。

树的高度不可能无限高，因为其受规模法则的约束。树的体积和重量与树的尺寸的立方成正比，而树的支撑力量由树的横截面积决定，也就是与树的尺寸的平方成正比。如果把树的高度扩大10 倍，那么其体积和重量将扩大到原来的1 000 倍，而它的支撑力只会变成原来的100 倍。树需要用100 倍的力量去承担1 000 倍的重量。如果树一直长下去，早晚有一天树将无法承担它自身的重量。

图7 中央小区对外出行量与城市尺度关系曲线Fig.7 Relationship between city scale and travel demand between city centers and outside groups

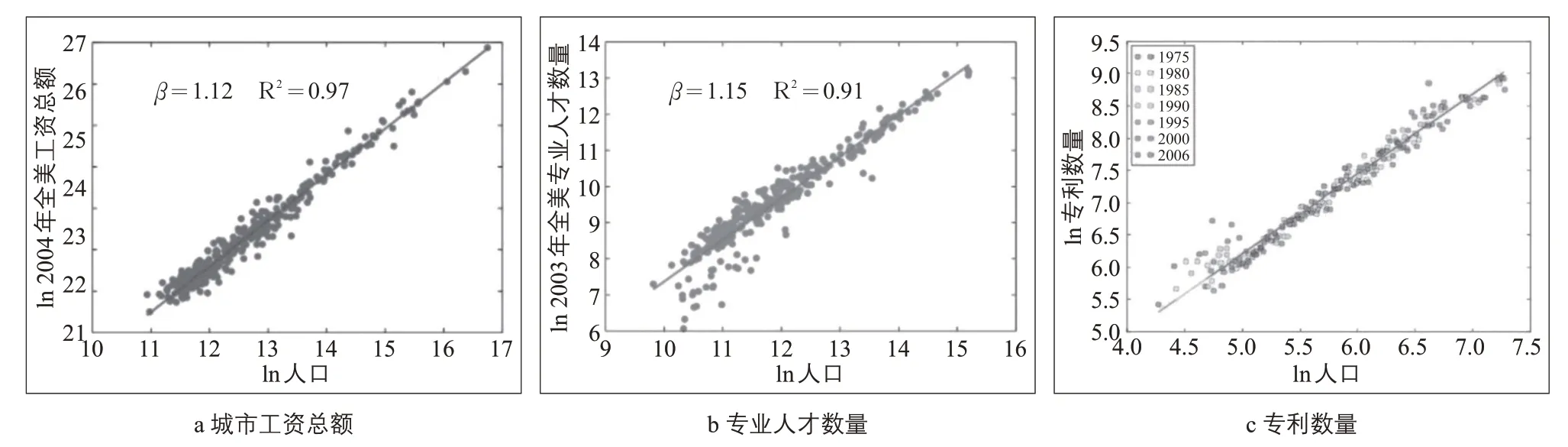
图8 美国城市各项指标与城市规模的关系Fig.8 Relationship between urban indicators and city scale in U.S.cities

城市规模也存在同样的问题。如果不考虑基础设施的承载能力，城市是越大越好。然而城市的交通承载力却是有限的，不可避免地导致城市规模越大，交通越堵。尽管有些城市通过用地与交通的协调、强化交通管理等缓解了交通拥堵的部分问题，但总体而言，还是呈现出城市规模越大交通越堵的趋势。在交通拥堵影响到城市的正常运行之后，就应该控制城市规模。例如北京提出的疏解首都非核心职能，从缓解交通拥堵的角度非常有必要。

当然，城市规模还与交通技术水平相关。城市的半径大致等于居民在1 h 内所能达到的距离：在步行时代，城市半径大约在4 km以内；公共汽车时代，城市半径可达到8～10 km；轨道交通、小汽车时代，城市的半径能超过25 km。

2）不同规模城市之间不能简单比较交通拥堵水平。

城市规模越大，交通总是倾向于越拥堵，不同规模城市的拥堵指数不宜简单地进行横向对比，可以采用分组或者利用标度律折算后再进行比较。基于此的交通拥堵比较和交通缓堵计划，才能更符合城市自身的发展规律。

3）享受大城市经济便利性的同时，也需要承担更多的交通成本。

城市规模越大，可以为城市带来更加经济便利的条件和更加有效率的产出，但同时也必须承受交通更加拥堵的事实。城市可以通过各种措施缓解拥堵，但大城市势必需要付出更多的成本。文献[12]指出国外部分学者认为拥堵是经济发展的伴生现象，可以根治拥堵的方法唯有经济衰退。在经济不断增长的前提下，新的交通设施供给会吸引新的通过性需求，同时吸引新的城市功能集聚，最终不但不会减少拥堵，反而会使拥堵加剧。

图9 中国城市人口规模和地区生产总值的标度律Fig.9 Scaling laws of urban population and gross domestic product in China

5 结语

在规模法则的作用下，总体上城市越大越好，城市也总是倾向于越长越大。一方面，城市越大基础设施越集约，另一方面，城市规模越大产出越高。但当交通需求超出交通承载力时，交通拥堵就会产生，而且呈现城市规模越大交通越堵的规律。树不可能无限长高的客观规律告诉我们，城市也不能承受无限变大，城市规模应与交通承载力相协调。本文借用复杂系统理论中的规模法则理论研究交通拥堵的本质，相关的基础理论还有待进一步完善，同时也需要收集更多的数据来验证本文所揭示的交通拥堵机理。造成城市交通拥堵的因素众多，如城市空间结构、交通方式构成等也会对道路交通拥堵产生重要影响，亦需要对此进行继续研究。