水库群调度效益与风险综合影响定量分析
2019-06-25高翔
高 翔
(辽宁省水文局鞍山分局,辽宁 鞍山 114000)
径流预报的准确度与可靠度对于水库调度方案的制定至关重要[1],对整个系统的经济、生态效益产生直接的影响。一方面单一水库的径流预报准确率对水库调度产生直接影响,另一方面水库群的综合调度存在较为复杂的非线性变化特征,这样也使得各水库径流预报的不确定呈现一定的叠加效应,因此径流预报对于整个流域水量分配具有重要的作用,为此在水库群系统调度中需要重点考虑径流预报的不确定性影响。近些年来,受限于复杂的影响要素和科学手段,径流预报的不确定性影响研究还处于探索分析阶段[2],主要采用确定性模型和随机模型进行径流预报的不确定性分析[3- 6],然后确定性模型主要依据与实测径流资料进行分析,很难满足水库调度的实时需求。随机模型分析时未能耦合实时信息,需要进一步改进,需要更深入的探讨径流预报不确定性和预报精度之间的相关性。当前,径流预报的不确定性对水库影响在效益层面[7- 9],对于风险分析研究还较少,而水库群风险分析对水库调度决策十分重要。为此本文结合辽宁地区的水库群数据,重点探讨径流预报不确定性对水库群效益和风险的综合影响。这样既可以通过风险决策来指导径流预报,又可通过径流预报结果对风险决策进行预估。
1 研究方法
1.1 自适应水量调度模型
以缺水量为最小目标构建一级目标方程,计算方程为:
(1)
以发电量最大为目标构建二级目标方程,计算方程为:
(2)
式中,ΔQi,j—第i个水库在第j个时段的缺水量额度;Ki—水库群在第i年的蓄满状态,当水库蓄满时,其值为1,未蓄满时,其值为0;M—水库个数;T—时段计算总数;N—计算时段统计年数。
此外,还需要满足以下约束条件。
各水库之间水力关联约束条件:
Ii,t=Qi-1,t+Si-1,t+Si,t-Gi,t
(3)
水库之间水量平衡约束条件:
Vi,t=Vi,t-1+(Ii,t-Qi,t-Si,t-Gi,t)·Δt
(4)
水库库容约束条件:
VLi,t≤Vi,t≤VUi,t
(5)
流量约束条件:
QLi,t≤(Qi,t+Si,t)≤QUi,t
(6)
水库出力约束条件:
PLi,t≤Ai·Qi,t·Hi,t≤PUi,t
(7)
模型边界约束条件:
Zi,0=Zi,startZi,t=Zi,end
(8)
式中,Qi,t—第i个水库在第j个时段的发电流量;Ii,t、Si,t、Ri,t、Gi,t—第i个水库在第j个时段的入库、弃水、区间入流以及供水流量;Vi,t、VLi,t、VUi,t—第i个水库在t时段的蓄水量值、可蓄水量最大和最小值;QLi,t、QUi,t—水库下泄流量的最大值和最小值;PLi,t、PUi,t—水库出力的最大值和最小值;Zi,start、Zi,end—水库起调和调度末期的库水位值。
1.2 水库群风险评价方法
1.2.1发电风险因子评价
结合整个水库群年发电量作为发电风险评价的主要因子,计算方程为:
η=KqHh
(9)
(10)
式中,K—出力系数;η—水库群总效率;q—发电流量;E—年度总发电量;i—计算水库个数;H—水库发电水位。
在发电量分析的基础上计算其发电风险评价因子,计算方程为:
Risk(S1)=P(E实际-E预期)
(11)
式中,Risk(S1)—发电风险评价指标;E实际—水库实际发电量;E预期—水库某一个时段内预期发电量。
1.2.2供水风险因子评价
本文引入改进的缺水指数来对水库的供水风险因子进行评价,方程首选确定水库的缺水指数,计算方程为:
(12)
式中,MSI—改进的水库缺水指数;T—调度时段总数;TSt—t时段缺水量;TDt—t时段水库需水量。
在水库缺水指数计算的基础上,计算供水风险因子,评价方程为:
Risk(S2)=P(MSI实际>MSI预期)
(13)
式中,Risk(S2)—发电风险评价指标;MSI实际—水库实际供水量;MSI预期—水库某一个时段内预期供水量。
1.2.3生态风险因子评价
本文采用生态供水缺损指数进行水库群生态风险因子评价,其评价方程为:
Risk(S3)=P(MSQ实际>MSQ预期)
(14)
式中,Risk(S2)—生态风险评价指标;MSI实际—水库实际生态供水量缺损指数;MSI预期—水库某一个时段内预期的生态供水量缺损指数。
2 计算步骤
水库径流预报的不确定性主要依据其预报精度的等级,本文主要探讨预报不确定性对水库群调度风险的影响,为此需要对径流自身不确定的风险影响进行排除,采用以下方程进行随机径流的计算,计算方程为:
Qft=Qst+ket
(15)
式中,Qft—预测径流;ket—径流预报误差;通过变化改变系数k来推求不同预报精度;Qst—枯水年份的实测径流量值。
主要计算步骤为:
(1)结合区域内2000—2017年实测径流数据,以枯水年份作为基础年份,枯水年份的实测径流作为基础径流数据。
(2)结合式(15)计算不同方案分析随机的径流组合,进行输入集合的生成。
(3)把径流输入组合应用到构建的流域水库群自适应水量调度模型进行计算,生成水库群调度结果集合。
(4)结合调度结果,应用各指标风险评价因子计算方程分别计算各水库的发电、供水以及生态风险评价因子,定量分析不同径流预报精度下的水库群效益与风险综合影响。
3 研究结果
3.1 研究区域概况
以辽宁地区浑太河流域的6座大中型水库进行径流预报不确定下的水库群调度效益与风险综合分析,浑太河为辽宁省主要河流之一,整个流域面积为27327km2,河流的总长度为450km,贯穿辽宁省6座城市,本文选取流域内6座大中型水库,各水库主要特性参数见表1。

表1 选取的水库基本信息
3.2 浑太河主要水库风险调度分析
以系数k来调整水库不同径流预报的精度,分别对6座水库不同径流预报精度下的各风险评价指标进行分析,分析结果如图1所示,并定量分析各水库不同风险指标与预报精度的变化趋势,结果见表2。
图1为各水库不同径流预报精度下的各类风险指标的变化趋势,其中k系数用来调整径流预报精度,从图1可看出,无论各水库径流预报精度如何调整,其中枯水季节的供水风险均为100%,对干流水库而言,来水量相比于支流水库较为丰富,因此缺水变幅波动较小。各水库发电和生态风险在不同径流预报精度下凸二次函数的变化趋势逐步增加。对单个水库而言,大伙房水库不同径流预报精度对其发电风险和生态风险均较大;而在观音阁水库,这种影响变化有所减低。对葠窝水库而言,不同径流预报精度对其发电风险大于生态供水风险。对于支流的三个水库而言,其不同径流预报精度的发电风险低于生态风险。从表2中可看出,从拟合度角度可看出,各水库不同径流预报精度和水库风险指标之间的拟合度均在0.65以上,干流水库的拟合度更高,支流水库的拟合度低于干流水库。
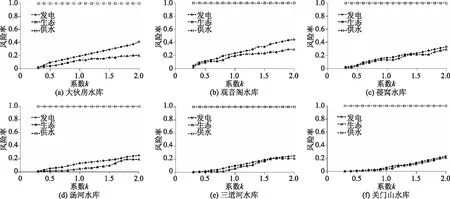
图1 浑太河流域水库群调度风险趋势分析结果

水库名称风险指标趋势线相关系数R2大伙房水库观音阁水库葠窝水库汤河水库三道河水库关门山水库发电风险Risk(S1)=-0.00078k2+0.3354k-0.07870.8452供水风险Risk(S2)=1/生态风险Risk(S3)=-0.0085k2+0.078k-0.08150.7493发电风险Risk(S1)=-0.0007k2+0.2487k-0.03850.7952供水风险Risk(S2)=1/生态风险Risk(S3)=-0.0096k2+0.085k-0.08480.7452发电风险Risk(S1)=-0.0013k2+0.3148k-0.08250.7643供水风险Risk(S2)=1/生态风险Risk(S3)=-0.0096k2+0.078k-0.07570.7152发电风险Risk(S1)=-0.0013k2+0.4152k-0.08350.7235供水风险Risk(S2)=1/生态风险Risk(S3)=-0.0085k2+0.013k-0.07820.6943发电风险Risk(S1)=-0.0017k2+0.4852k-0.06530.6742供水风险Risk(S2)=1/生态风险Risk(S3)=-0.0078k2+0.056k-0.08230.6515发电风险Risk(S1)=-0.0009k2+0.4412k-0.08530.6948供水风险Risk(S2)=1/生态风险Risk(S3)=-0.0089k2+0.132k-0.15430.6506
3.3 浑太河主要水库风险调度分析下径流预报精度要求分析
为定量分析浑太河主要水库径流预报的不确定性对其水库各风险指标的影响,假设各风险指标低于15%,则各水库径流预报的精度要求见表3。
从表3可看出,当各水库的风险评价指数低于15%的情况下,预报精度的纳什系数均需要达到0.66以上;在枯水季节,各个水库的调度风险受到径流预报不确定性影响变幅较大,稍有波动就会对各个水库的风险指数产生较大程度的影响,因此对枯水季节的径流预报精度要求较高。
3.4 浑太河主要水库群干流和支流风险调度分析
在各水库不同径流预报精度下干流和支流的水库风险分析的基础上,对浑太河主要水库群的干流和支流风险调度变化趋势进行分析,如图2所示,分析结果见表4。
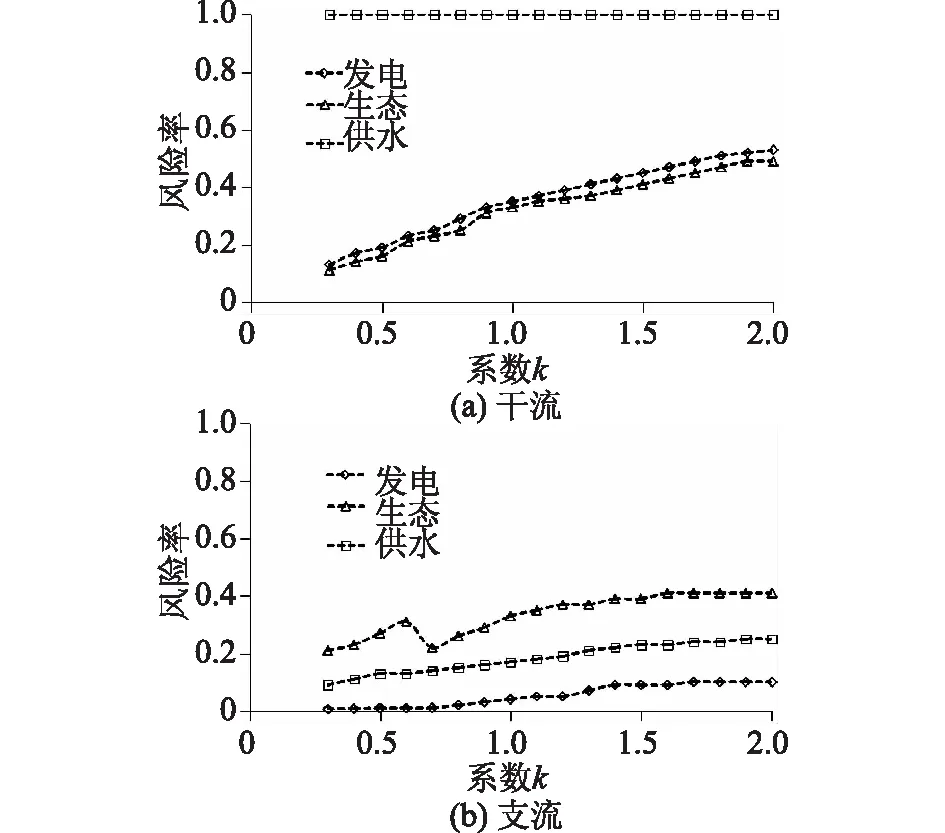
图2 不同预报精度下浑太河梯级水库群干流和支流风险变化趋势结果
从分析结果可看出,浑太河流域主要干流水库群受径流预报不确定影响主要体现在发电和生态风险上,且对于同一个径流预报精度下,干流水库群的发电风险要大于生态风险,由于在枯水季节,径流预报的不确定性对供水风险影响程度较低,从图2可看出,支流径流预报的不确定性影响主要体现在支流水库群的供水和生态风险上,在同一个径流预报精度上,水库群供水风险要大于生态风险,而径流预报的不确定性对支流水库群发电风险的影响程度较低,低于其他两类风险指标。从表4可看出,对于同一个径流预报精度而言,浑太河水库群的风险指数大小排序为:供水风险>发电风险>生态风险,整个流域水库群的调度风险和径流预报精度也呈现二次凸函数的变化关系,其趋势线的拟合度在0.65以上。
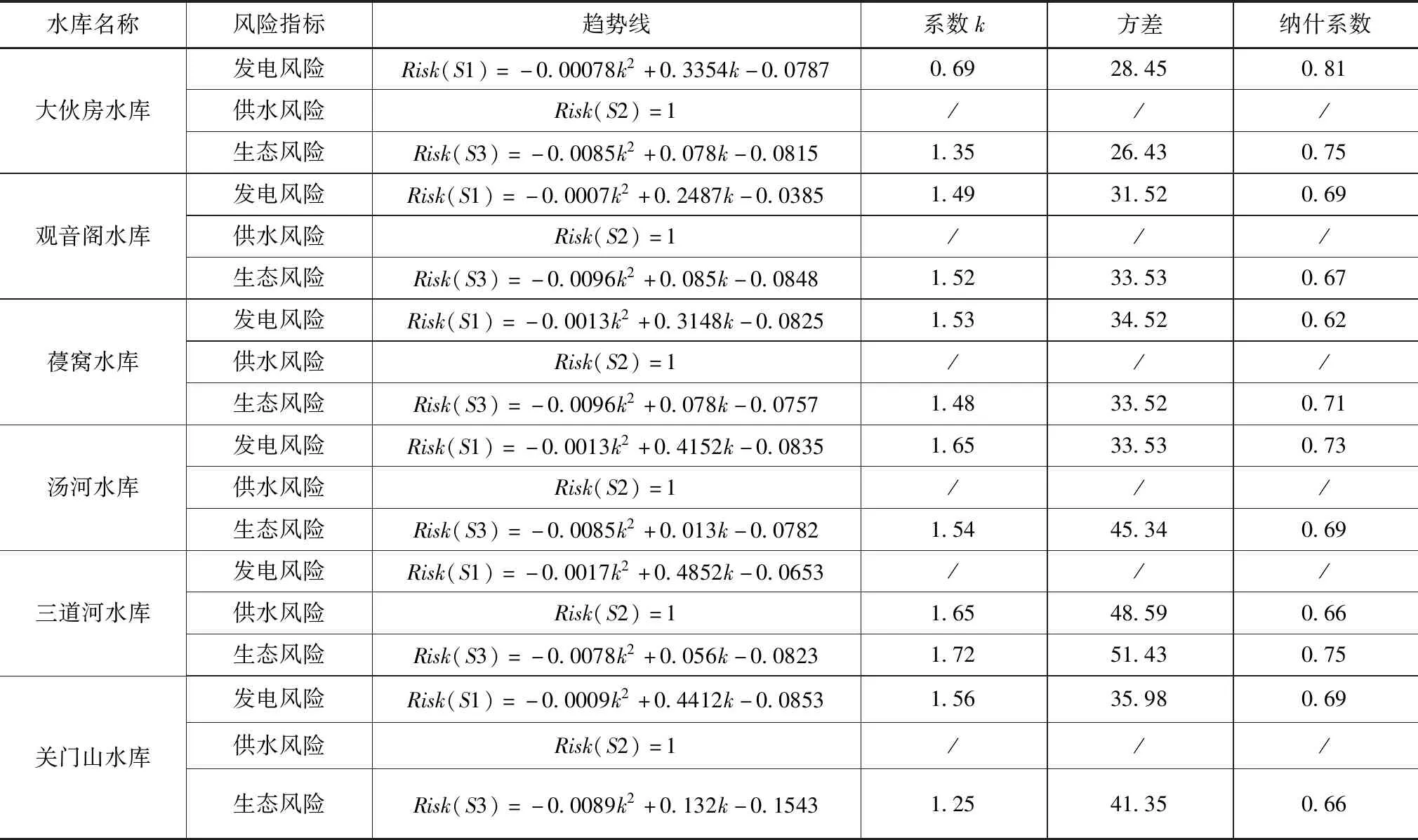
表3 浑太河流域主要水库群风险分析下径流预报精度需求分析
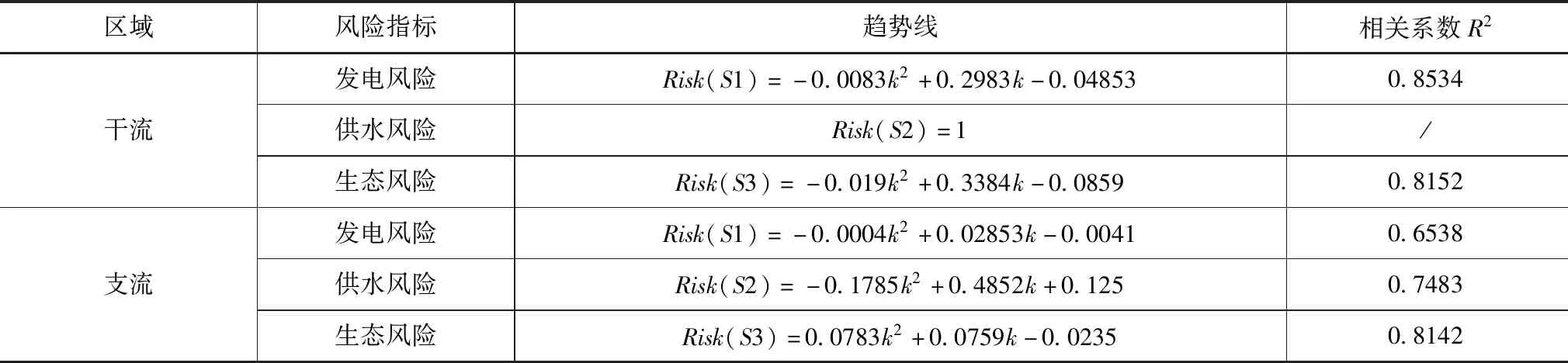
表4 不同预报精度下浑太河梯级水库群干流和支流风险变化趋势线
4 结语
结合径流预报的不确定性分析其对水库群效益及风险的综合影响,这样可以提高水库径流预报的精准性,以大伙房水库为例,当需要保证水库发电和生态风险均低于15%时,预报精度的纳什系数需要达到0.81;对于同一个径流预报精度而言,浑太河水库群的风险指数大小排序为:供水风险>发电风险>生态风险。
本文主要考虑径流预报的不确定性对水库群兴利效益的影响,对于水库群而言,防洪风险不能忽视,在以后的研究中还需要重点考虑径流预报不确定性和防洪风险的关系。
