辽宁省最严格水资源管理类型识别与研究

2019-06-25李华欣

水利规划与设计 2019年6期

李华欣

(庄河市林业水利服务中心，辽宁庄河 116400)

水资源管理格局与最严格水资源管理制度之间具有密切关系，关于最严格水资源管理政策措施、指标体系等方面的内容许多学者进行了深入解读和探讨，并取得了卓有成效的研究进展[1]。目前，可变模糊法、神经网络法、物元分析法以及层次分析法等是较为常用的最严格水资源管理评价方法，并且各方法在一定环境条件和区域范围内均取得了较好的应用效果。然而，在最严格水资源管理评价时同样存在一些不容忽视的问题和不足，主要体现在：在社会经济发展水平、水资源禀赋以及承载力等方面，我国南北方区域之间存在一定的差异，目前还未形成统一、完善的分级标准和评价体系，仅仅从万元工业增加值用水量、用水控制率、水功能达标率等方面难以客观、全面的反映最严格水资源管理状态；评价方法存在不足，如对指标权重利用AHP法确定具有一定的主观随意性、神经网络法具有训练过于拟合和结构不确定性、物元分析法设计函数较多且规律性较差，可变模糊法确定权重具有较大的困难等；最严格水资源管理的影响因素往往涉及到水环境、社会经济、水资源等多个方面，然而参与评价的指标仅从纳污控制、用水效率、水资源总量等方面选择，因此难以客观、全面的反映区域真实水平[2]。

根据以上分析和相关文献，本文选择能够较好处理非线性、高维典型问题的投影寻踪法，客观、科学的识别了辽宁省各区域最严格水资源管理类型，并验证了OFA-PP模型的有效性与可行性，以期为促进该区域水资源可持续利用和管理配置提供一定借鉴。

1 最严格水资源管理评价体系与标准

本文参考最严格水资源管理相关文献和考核标准，在遵循代表性、可行性、可量化性原则的基础上，分别从水环境条件、水资源禀赋以及社会经济发展水平3个方面选择评价指标，并建立了评价体系[5]。然后根据纳污能力、用水效率以及用水总量控制红线，将最严格水资源管理类型划分为Ⅰ～Ⅴ级5个分级标准，结果见表1。

2 基于OFA-PP模型的类型识别

2.1 OFA理论简介

文献提出的基于最佳觅食理论与行为生态理论的新型群体智能算法即为OFA最优觅食算法，该方法主要是通过模拟觅食中心位置、食物地域、猎物识别时间以及动物觅食搜索等过程构建数学模型[3]，针对待优化问题可根据最大觅食动物能力进行求解，OFA数学法主要流程如下：

(1)初始化动物觅食位置。生物觅食是自然界中的生命基础，不同类型生物的觅食行为存在一定差异。对OFA中的个体可根据最佳觅食理论作为一种觅食动物，待优化问题的可行解即为其位置分布。对第t+1代觅食空间在d维初始化中的位置可按照下述公式确定，计算方法为：

表1 最严格水资源管理评价体系与分级标准

注：供水模数T4单位为104m3/km2；属性“+”、“-”分别为越大越优型、越小越优型指标。

(1)

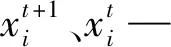
(2)觅食位置增量描述。参考已有文献并利用式(1)，可运用下述数学公式描述个体i在第t代觅食位置增量，如下所示：

(2)

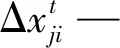
个体在OFA中发现更好的位置后，将一一搜索生物群体中每个个体的空间位置并通向该位置；若当前个体本来就是最好，则可通过搜索最差个体从而确定其附近更好的位置。群体中每个个体都可以按照式(2)，在OFA中逼近当前个体的位置，在群体中除最优个体外都向更好的位置移动。

(3)识别猎物。如果只有两种猎物存在觅食活动，则可根据最优觅食理论将其分为有利可图1和无利可图2两种类型[4]。为了摄入更多的能量，动物总是选择更好的猎物，因此在觅食过程中动物可忽略无利可图猎物，并根据如下公式识别更好的猎物。

(3)

式中，E1、E2—猎物1、2的净能量收益；h1、h2—处理猎物1、2所需要的时间；λ1—相遇率，即动物遇到猎物2的比率。

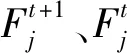
(4)

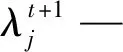
对OFA改进时，其比例引起为k=t/T，因此可分别设定较大与较小的比例因子，从而更加有利于全局和局部的搜索。采用粒子群优化惯性权重改进法平衡OFA的局部与全局搜索能力，并对比例因子k采用系数法改进，其表达式为：

k(k+1)=η×k(t)

(5)

式中，η—比例因子衰减系数，本文中其值为1.00。

2.2 投影寻踪模型

根据遗传投影寻踪模型的特点和函数特征可将其计算流程大致分为以下几个步骤：

(1)归一化处理。不同评价指标的量纲和单位存在一定的差异，为消除评价指标之间的不可通透性，需对各指标进行变化范围的标准化归一处理[5]。对于正向指标可利用下述公式进行标准化归一处理。

(6)

对于负向指标可采用下式进行标准化归一处理。

(7)

式中，xmin(j)、xmax(j)—样本中第j个指标的最小值和最大值。采用上述公式可将各评价指标值统一处理至0～1的范围之内。

(2)构造投影函数。通过将{x(i，j)|j=1，2，∧，p}的p维数据综合成一维投影值即为投影寻踪模型，其一维投影方向为a=(a(1)，a(2)，∧，a(p))，投影公式如下：

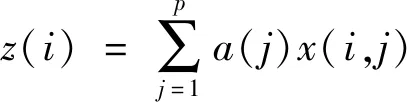
(8)

式中，a—单位长度向量。

(3)模型的优化求解。投影指标函数Q(a)在方案集确定的条件下仅随投影方向a的改变而发生变化，因此可依据投影方向作为数据特征状况，即出现可能性最大的方向即为高维数据特征最佳投影方向。利用最大化估计法可对投影方向的最佳方向进行求解，可采用下式进行目标函数的求解。

max:Q(a)=SzDz

(9)

其约束条件为：

(10)

式中，Sz、Dz—投影值z(i)的标准差和局部密度，其计算公式分别如下所示：

(11)

(12)

式中，Ez—投影值序列的均值；R—局部密度的窗口半径，可利用经验公式进行求解，通常为αSz，其中α为0.1、0.01或0.001等，可结合在区间内投影点的分布状况进行调整。

2.3 模型识别流程

步骤一：对辽宁省各区域最严格水资源管理分级标准阀值和指标数据运用式(6)—(7)进行归一化处理，然后运用标准化处理后的数据分别构建准则层纳污能力、用水效率和用水总量控制红线的目标投影函数，即QP(a)、QE(a)、QT(a)。

步骤二：设定OFA种群的衰减系数η、最大和当前迭代次数T与t、问题维度d、种群规模N，然后随机生成个体的初始觅食位置并对目标函数QP(a)、QE(a)、QT(a)利用OFA优化求解，对目标函数值进行计算和排序。

步骤三：对个体新的觅食位置利用式(2)进行更替运算，然后对下一次迭代方向运用式(4)进行搜索。如果符合公式计算条件，则保存用于下一次迭代搜索的第t+1次搜索后获得位置；否则，忽略在t+1次搜索的位置并将第t次的位置保存进行下一次的搜索。

步骤四：优化改进衰减系数η并判断算法终止条件，如果满足终止条件可输出最佳个体位置，结束计算；否则，重复上述计算直至达到终止条件。

步骤五：输出最佳个体空间位置及其相应的目标函数值，即完成对最佳投影向量aT、aE、aP和函数值maxQr、maxQE、maxQP。对辽宁省各区域最严格水资源管理分级标准阀值以及综合投影值根据最佳投影向量aT、aE、aP确定，并识别评价各区域管理类型。

3 实例应用

3.1 数据来源

辽宁省位于我国东北部地区，下设14个省辖市和27个县，属于大陆性季风气候，年降水量在600～1100mm。由于其独特的地理特征和环境气候，年际水资源量呈现出典型的周期性丰枯变化特征，其中75%以上的降水量集中在汛期6—9月，并多以暴雨和强降雨的形式出现。水资源补给以大气降水为主，主要包括降水入渗补给和地表径流量两大部分，年均水资源量约为341.79亿m3。境内主要包括大凌河、辽河、浑河、太子河和绕阳河等河流，东南部与渤海相邻水源面积较大，降水量较为充足，而西北区域降水较少并且风沙干旱现象较为频繁。该区域水资源管理存在的问题主要有供需矛盾突出、降水量时空分布不均、用水效率低、水资源利用方式粗放以及局部地区水环境恶化等问题。辽宁省各区域经济发展不平衡，用水水平存在一定差异，因此研究识别14个地区的最严格水资源管理类型对于促进该区域水资源可持续利用和优化配置具有重要意义[6- 13]。本文所需各指标初始数据，来源于辽宁省2016年统计年鉴、水资源公报、政府工作报告等资料。

3.2 目标函数的优化

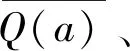
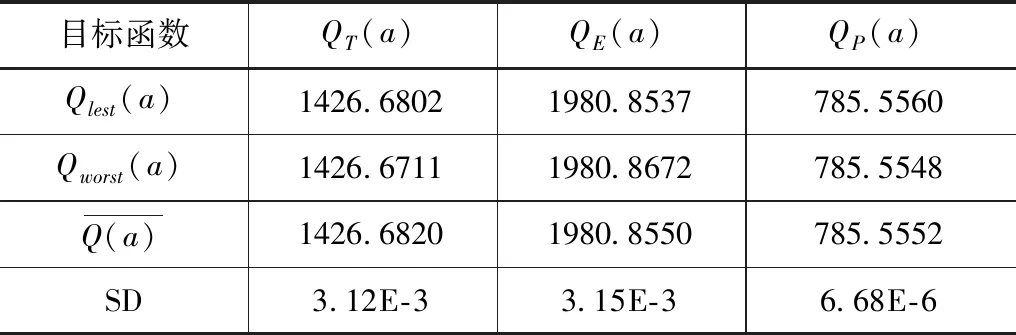
表2 最严格水资源管理目标函数值优化结果

然后对模型进行运行求解可得到最优投影向量，分别如下：

3.3 结果分析

根据目标函数输出结果，模型标准差低于3.12E- 3，表明在最严格水资源管理区域类型识别过程OFA模型具有较好的稳健性和计算精度。然后对辽宁省各区域的综合投影值zT(i)、zE(i)、zP(i)和“三红线”的类型识别分级标准值zT(k)、zE(k)、zP(k)，根据最佳投影方向aT、aE、aP进行求解，见表3—4。

表3 最严格水资源管理类型识别标准

表4 辽宁省各区域“三红线”类型识别

根据上表计算结果可知，辽宁省14个区域的最严格水资源管理用水总量、用水效率、纳污能力控制红线的类型识别依次为：大连市为“Ⅰ级-Ⅱ级-Ⅲ级”型；沈阳为“Ⅲ级-Ⅱ级-Ⅲ级”型；鞍山为“Ⅱ级-Ⅱ级-Ⅳ级”型；抚顺为“Ⅳ级-Ⅳ级-Ⅳ级”型；本溪为“Ⅲ级-Ⅲ级-Ⅳ级”型；丹东为“Ⅳ级-Ⅳ级-Ⅲ级”型；锦州为“Ⅳ级-Ⅳ级-Ⅳ级”型等等。根据各区域水资源管理识别类型，提出了“四项制度”、“三条红线”管理办法从而提高辽宁省水资源可持续利用和管理水平。