考虑设备不同作用位置的动力相互作用影响研究

(1.天津大学 建筑工程学院，天津 300072；2.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072)

0 引言

随着经济发展和科技进步，建筑结构的形式朝着大型化和复杂化方向发展，大量的功能性建筑设备和装饰性非结构构件依附于建筑主体结构安置，由于设备与结构的不同动力特性，形成了具有独特动力特性的设备-结构动力相互作用体系。在以往的建筑结构设计中，建筑主体与设备的设计往往侧重于其工艺上的协调，对设备-结构耦合体系的抗震性能关注不够。而在地震实际作用过程中, 结构与设备是共同工作的且二者之间存在着复杂的动力相互作用，忽略这种影响对结构-设备耦合体系进行抗震分析，就不能正确反映结构内部的地震作用分布，在某些情况下，可能会使设计结果偏于不安全。

对于设备-结构体系研究主要有两种方法，一是基于楼面反应谱的研究方法，二是基于耦联系统的动力分析方法。近年来，国内外对于设备-结构体系动力相互作用的研究取得了一定的进展和成果。对于楼面反应谱的研究：苏经宇等[1]提出了楼面反应谱的简化方法；国巍等[2]深入研究了水平双向地震作用下影响偏心结构的楼板谱变化的几个重要参数，诸如附属结构质量、附属结构位置等；秦权等[3]用随机振动法建立了楼面反应谱分析程序FASP。对于耦联系统的动力分析方法的研究：姜忻良等[4]提出了适合于局部非线性的混合动态子结构法，研究了设备非线性参与结构分析的设备与结构相互作用影响；李杰等[5]分析了设备-结构耦合体系的动力特性及其抗震性能，并对对称结构体系与非对称结构体系的地震反应差别等问题进行了深入研究。目前，人们对于设备-结构体系动力相互作用的研究主要集中在设备-结构之间耦合效应、考虑非线性设备与线性结构耦合作用、单个附属设备及多个附属设备结构耦合作用、设备与结构阻尼比、频率比、质量比和非经典阻尼特性的影响以及相关计算方法等方面。但是，关于设备偏心布置对于设备-结构耦合体系中设备及结构动力相互作用影响方面的研究还有待进一步深入。另一方面，在实际的建筑结构中，有时为满足结构的特殊功能要求，设备的偏心布置往往是不能避免的，由于设备的偏心布置某种程度上会造成设备-结构耦合体系的质量偏心，当设备与结构的质量比不很小时，必然会引起结构主体不可忽略的扭转效应，进而会影响设备、结构在地震动作用下的动力响应。因此，深入研究设备偏心布置对设备-结构体系动力相互作用的影响具有非常重要的理论和现实意义。

以某十层钢框架建筑为例，利用ANSYS有限元分析软件建立了三维空间分析模型，对设备-结构相互作用体系在El Centro波、Taft波和人工波3种不同地震动作用下的动力时程响应进行分析，研究了设备单向偏心布置对设备、结构动力相互作用的影响。

1 分析模型和运动方程

1.1 有限元模型建立

设备-结构相互作用体系结构立面图以及结构平面图，分别如图1、图2所示：结构主体为10层钢结构，模型平面尺寸为31.2 m×31.2 m，首层层高3.9 m，2～9层层高3.6 m，第1～9层包括结构和非结构每层的总抗震质量为6.25×105kg，第10层总抗震质量为5.65×105kg，其中楼板及其上配重块质量等效为线荷载施加于相应楼层主、次梁上。结构系统模型梁柱尺寸见表1，其中钢材型号为Q345，泊松比为0.3，弹性模量取为2.0×105MPa，由于钢材翼缘厚度介于16 mm和35 mm之间，计算时按照规范钢材的屈服强度取为310 MPa。设备质量取3.10×105kg，为结构总抗震质量的5%，作用于结构顶层，高度为2 m，考虑到抗震设计中的设备，通常指的是固定于建筑结构的附属设备的支架，并不包括设备本身[6]，据此将设备简化为圆钢管与质量块组成的单指点自由度体系。ANSYS分析模型中梁柱均采用BEAM189单元模拟，一层柱单元尺寸为0.975 m，2～9层柱单元尺寸为0.9 m,结构梁的单元尺寸为0.975 m，设备单元尺寸为0.5 m，设备-结构体系单元总数为6 764个。结构梁柱之间的连接方式为刚接，设备与结构通过变形协调连接在一起。

对结构做如下假定：①采用刚性地基假定，底层柱与地基固结；②质量矩阵基于一致质量矩阵；③材料的本构模型为双线性等向强化模型，取屈服后刚度为屈服前的1%；④结构各层质心和刚心位于同一竖轴，均处于结构几何形心处；⑤设备偏心布置仅影响楼层的质心位置，楼层刚心位置不变，仍位于结构几何形心处。

图1 结构立面图(单位：mm)

图2 结构平面图(单位：mm)

表1 梁柱材料参数 mm

1.2 设备-结构体系运动方程

设备-结构体系的运动方程[7]为

阻尼矩阵C采用Rayleigh阻尼假定，即

C=αM+βK(2)

不考虑振型阻尼比，采用常阻尼比假定，即

(3)

2 设备-结构相互体系动力时程响应分析

2.1 地震动加速度时程曲线选取

图3 地震动加速度时程曲线

地震波选取适合三类场地的 El Centro波、Taft波和人工波，其采样周期均为 0.02 s，地震波的加载方向选定为结构的弱轴(即图2中的Y轴)方向。各地震动加速度时程曲线如图3。

2.2 设备位置对设备-结构动力相互作用影响

当附属设备在结构顶层偏心作用时，会引起结构顶层的质量偏心，使顶层质心与刚心发生偏离，在水平地震作用下,由于结构质心与刚心的不重合，使得结构产生附加扭转，导致结构产生扭转变形。如图2，设备在结构顶层沿Y向偏心时，引起结构的Y向质量偏心，而在Y向地震动作用下，地震力引起的惯性力既穿过结构的质心又穿过结构刚心，结构不会产生扭转震动，结构的地震反应仅为平移振动；而设备在结构顶层沿X向偏心时，引起结构X向的质量偏心，地震力引起的惯性力与结构的质心、刚心不共线，结构产生扭转振动，结构的地震反应不仅有平移振动还有扭转振动，因此设备沿X向偏心设置时对结构的动力反应影响较大，设备、结构动力相互作用更加明显。因此，为对比分析设备位置对设备-结构体系动力相互作用的影响，设计了3个设备不同作用工况(2个设备偏心作用工况和1个设备中心作用工况)。如图2，①工况1-附属设备作用在结构顶层位置1处(3轴与C轴交点处，即结构形心处)；②工况2-附属设备作用在结构顶层位置2处(2轴与C轴交点处)；③工况3-附属设备作用在结构顶层位置3处(1轴与C轴交点处)。定义ex、ey分别为结构顶层质心的x、y向坐标，即结构顶层的静力偏心距，ex=mexe/(me+m10)，ex=meye/(me+m10)，其中，me、m10、xe、ye分别为附属设备和主体结构第10楼层质量，附属设备x、y向坐标；bx、by分别为第10层x、y向偏心率(偏心率为偏心距与结构楼层回转半径的比值)，bx=ex/rx，by=ey/ry，由于结构各层的刚度中心和几何中心重合，有rx=w/2+ey，ry=l/2+ex，其中，l、w分别为结构平面长度和宽度。求得工况1、工况2以及工况3的偏心率分别为0、15.5%和26.16%。

2.2.1 模态分析

提取前5阶振型的自振频率，3种工况模型的自振频率和自振周期如图4和表2所示。

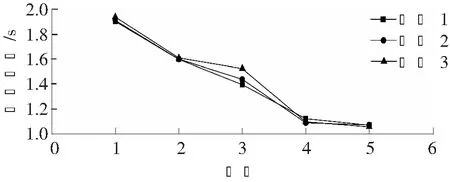
图4 设备作用3工况前5阶自振周期对比图

阶数工况1周期工况2周期工况3周期11.901.911.9421.601.601.6131.401.441.5241.121.091.1051.071.071.06

由图4及表2可知，结构基本周期约为1.9 s，3种工况第三阶自振周期差异明显，其余阶自振周期基本一致。模态分析结果表明，结构前三阶振型模态分别为：Y向平动、X向平动和扭转振动，结构第三阶振型自振周期差异显著，说明虽然设备质量仅占结构总地震质量的5%，但设备偏心却会带来设备-结构耦合体系明显的扭转振型反应差异。下文将对3种工况下设备、结构动力响应对比分析，以期得到设备偏心对于设备、结构动力响应的影响规律。

2.2.2 结构动力反应分析

为研究设备位置对结构主体动力反应的影响规律，用El Centro波、Taft波、人工波对结构进行了分析计算，但由于篇幅原因，仅给出人工波作用下结构的动力反应计算结果。由于设备偏心会使结构产生平扭耦合地震反应，为深入分析设备作用位置对结构动力反应的影响，将结构位移反应分解成平动位移分量和扭转引起的水平位移分量进行比较分析。各层的质心处仅有平动位移，则各层的某一点的位移数据减去平动位移即为这一点的扭转平动位移。现分别取图2中左下角柱(定义为角柱1)位移和右下角柱(定义为角柱5)位移作为结构地震反应分析的参考指标。

(1)小震阶段。图5给出了人工波小震作用下不同设备作用工况结构的地震反应。可以看出，在小震弹性阶段，设备偏心对于结构层间平动位移反应的影响随着设备偏心的增大而增大；相对于设备中心作用工况，设备偏心使得结构层间平动位移反应有所增大，顶部楼层位移增大最为明显，在设备偏心设计时应适当加强结构顶部各层的抗侧刚度。当设备中心作用时(即工况1下)，设备不会引起结构的质量偏心，主体结构仍为对称结构，单向水平地震动作用下主体结构仅发生平移震动而不会发生扭转震动，因此工况1下结构角柱1与角柱2的扭转平动位移反应均为零。当设备在结构顶层偏心布置时，结构角柱的扭转平动位移反应随着设备偏心的增大而增大，相对于设备中心作用工况，设备偏心引起的结构扭转反应使得结构柔性边角柱(定义为靠近质心侧，即图2中的1轴与A轴交点柱)的位移反应有所增大，刚性边(定义为远离质心侧，即图2中的5轴与A轴交点柱) 的位移反应有所减小，说明设备偏心对于结构柔性边角柱的影响是不利的，在设备偏心设计时应注意这一不利影响，对结构柔性边予以加强；结构顶部各层扭平位移比大于1，说明顶部各层扭转效应大于结构的平动效应，在设备偏心设计时应当考虑结构顶部各层的抗扭设计。

图5 人工波小震作用下结构角柱位移分布图

(2)中震阶段。如图6所示人工波中震阶段结构层间平动位移及层间扭转位移变化与小震阶段相似，但与小震阶段相比不同工况之间的结构层间平动位移、扭转位移反应差异有所减小，其中扭转位移反应减小较为明显。引起这种变化的原因为中震作用下结构仍然处于弹性工作阶段而设备在一定程度上产生了塑性变形，造成设备刚度一定程度的降低，设备进入塑性变形后，设备与结构之间的相互作用力减小，使得设备对于主体结构动力反应的影响减弱，进而导致设备偏心对于结构的动力反应影响有所减小。

图6 人工波中震作用下结构边柱位移分布图

(3)大震阶段。如图7所示，大震阶段三工况结构层间平动位移与层间扭平位移分布图趋势走向与小震、中震阶段有一定的差异，主要表现为设备偏心引起的结构扭转反应，使得结构刚性边底部各层角柱位移反应有所增大，顶部各层位移反应减小，结构同一侧边柱不同楼层的扭转位移呈差异变化，同时与小震、中震阶段相比不同工况之间的结构位移反应差异进一步减小。造成这种现象的原因为：一方面，大震阶段设备塑性变形继续发展，刚度进一步退化，导致设备与结构之间相互作用力更大幅度的减小，设备与结构之间较小的相互作用力使得设备对于结构地震反应的影响变得微小；另一方面大震阶段结构部分构件也发生了屈服甚至破坏，导致结构抗侧刚度发生变化而使结构刚度中心发生改变，这种改变在地震作用过程中不断变化，使得设备偏心引起的结构偏心大小也在不断变化，从而导致结构地震反应受到设备作用位置的影响减弱。

图7 人工波大震作用下结构边柱位移分布图

上述对结构动力反应的分析结果表明，不同设备作用工况下结构动力反应有所不同，总体趋势为设备较大的偏心会引起结构较大的动力反应变化，说明设备偏心大小是影响结构动力反应的一个非常重要的因素；小震、中震、大震作用下结构动力反应的差异，说明设备偏心对于结构动力反应的影响与输入结构体系的地震强度大小有密切关系。

2.2.3 设备动力反应分析

为研究设备位置对设备动力反应的影响规律，本文选取设备顶层的位移时程响应作为设备分析的参考指标，其中设备位移是相对地面的绝对位移。

如图8～图10，不同地震动作用下3种设备位移时程曲线计算结果表明：El Centro波、Taft波及人工波小震作用下，设备偏心作用对于设备顶点最大位移的影响规律相同，设备偏心使得设备顶端最大位移反应相对于设备中心作用工况有所增大，其中Taft地震动作用下增大最为明显，工况2及工况3相对于工况1的增幅分别为8.2%和18.7%，但不同地震动作用下设备偏心引起的设备顶端峰值位移反应具有一定差异，说明设备的动力反应大小与输入的地震波密切相关。与小震阶段不同，El Centro波、Taft波及人工波中震、大震作用下，设备偏心对于设备顶点位移反应影响呈现差异变化。El Centro地震动作用下，中震阶段，设备偏心作用工况下设备顶点最大位移有微小增大而大震阶段却减小；Taft波中震及大震作用下，偏心工况下设备顶点位移相对于中心作用工况均减小；与Taft地震动作用不同，人工波中震及大震作用下，设备的偏心使得设备顶点位移反应却增大。可以看出不同地震动中震、大震阶段设备顶端位移反应具有较大差别，造成这种现象的原因为不同地震动作用下设备、结构的塑性发展差异所致。

图8 小震作用下不同设备作用工况设备顶端位移时程响应曲线

图9 中震作用下不同设备作用工况设备顶端位移时程响应曲线

图10 大震作用下不同设备作用工况设备顶端位移时程响应曲线

如表3所示，不同地震动作用下设备顶端峰值位移反应均值计算结果表明：小震阶段设备偏心增大了设备顶端位移均值反应，而在中震及大震阶段，则减小了设备顶点位移均值反应。这种现象的产生是因为，设备偏心导致结构质量偏心，地震波中震及大震作用下结构产生较大的扭转反应，扭转塑性变形耗散部分地震能量，使得输入到设备的地震能量有所减小，从而相应地导致偏心工况下设备顶端位移反应有所降低。不同地震阶段设备顶端位移的不同变化，说明设备偏心对于设备顶点位移反应的影响与输入地震波强度大小有密切关系。

表3 设备顶端峰值位移反应均值表

上述对设备动力反应的分析结果表明，在小震阶段设备偏心作用会使设备位移顶端的峰值位移反应增大，而在中震、大震阶段则使设备顶端峰值位移反应减小，说明地震强度是影响设备、动力反应的一重要因素；工况1、工况2及工况3设备顶端位移的差异反应，说明设备偏心大小也是影响设备地震反应的一项重要因素，设备偏心对设备位移反应的影响随着设备偏心增大而增大；设备在不同地震动作用下位移反应具有较大差异，说明设备的位移反应与输入的地震波密切相关。

3 楼面反应谱法与时程分析法比较

第一代楼面反应谱通过解耦直接给出了设备的加速度，通过楼面反应谱，就不再需要对主体结构进行分析，由附属结构自身的自振周期、阻尼和质量等特性就可以求得其地震力，具有极大的方便性。

由于设备总质量与主体结构总质量之比为0.05，设备频率与主体结构频率比为1.5，根据规范[8]，可以对设备-结构耦合体系进行解耦分析，同时将设备质量包括在主体结构质量内，依据时程分析法，计算得到图11楼面反应谱，并依据公式F=ηmSa计算出楼面反应谱方法下的设备地震力，并将计算出的地震力与时程分析法下地震力比较。

图11 小震、中震、大震楼面反应谱

由图11可知,不同地震波作用下的楼面反应谱具有一定的差别，以小震作用下的楼面反应谱为例，EL Centro 、Taft波作用下，楼面谱的最大值分别为 2.42 m/s2和2.12 m/s2，对应的周期均为 0.9 s，人工波作用下，楼面谱的最大值为 2.01 m/s2，对应的周期为 0.5 s。这也充分说明了地震动作用下设备的动力反应与输入的地震波密切相关。

由表4可知，时程分析法下设备偏心不会引起设备剪力反应的较大变化，说明设备偏心对于其自身的地震反应影响较小，反应谱法与时程分析法下的设备剪力计算值比较可以看出，反应谱法下设备地震反应大于时程分析法，小震阶段两种方法下的地震反应比值最大可以达到1.58倍，可见楼面反应谱法计算结果偏于保守，考虑到工程的经济效益有必要对设备-结构体系进行耦合作用分析。中震、大震阶段两种方法下的计算结果差距进一步加大，楼面反应谱下的地震反应已基本失真。究其原因是中震、大震作用下结构部分塑性的发展导致了楼面反应谱的较大误差[9-10]。

表4 设备剪力 kN

4 结论

本文利用ANSYS有限元分析软件，对设备-结构动力相互作用体系进行了全面系统的动力反应分析，讨论了在不同的地震阶段设备在顶部楼层偏心作用对结构及设备的动力响应的影响，并进行了楼面反应谱法及时程分析法下设备动力计算结果对比分析。得到如下结论。

(1)设备-结构相互体系中设备偏心布置对于结构与设备反应有不同的影响，具体计算结果不仅与设备偏心大小有关，而且与地震波性质密切相关。

(2)顶部楼层设备偏心使得结构顶部楼层产生较大的扭转反应，这一扭转反应使得结构柔性边角柱动力响应显著增大，设备偏心设计时应适当加强结构顶部楼层的抗扭设计。

(3)在经历小震、中震、大震的过程中，设备偏心对结构及设备的影响明显不同，一般来说，中震、大震阶段由于设备、结构先后进入了弹塑性阶段，刚度等主要参数发生了变化，导致设备与结构之间的相互作用降低，进而使得设备偏心对结构及设备的动力反应的影响降低。

(4)楼面反应谱法设备计算结果偏于保守，结构塑性的发展甚至可以导致楼面反应谱法设备地震反应计算的失真，考虑到工程的经济效益有必要对设备-结构体系进行耦合作用的动力时程分析。

以上是在单向地震波输入，设备单向偏心作用情况而得到的结论，在设备-结构相互体系双向地震波输入以及设备双向偏心布置对于设备、结构动力响应的影响还有待研究。