解题教学要教学生学会思考——从一道较难填空题的讲评说起

筅江苏省江阴市高新区实验中学 任 维

中考复习最后阶段，会进行一些模拟考试，这些试卷中都会有一些把关题，命题者往往会设置在选择、填空或解答题的最后一题位置，这些试题也成为讲评的重点任务，是核对解答式的讲评还是精心设计之后开展更有品质的习题讲评呢？这是值得我们认真思考的一个现实课题.本文从最近一道较难的中考模考卷填空题讲评设计说起，谈谈在解题教学中实现教学生学会思考的一些做法与体会.

一、从一道较难填空题的讲评说起

考题：若抛物线y=x2+bx（b＞2）上存在关于直线y=x成轴对称的两个点，则b的取值范围是______.

考题分析：这道题从答题情况来看，班里没有学生做对，全年级也只有不到2%的正确率，说明这道考题很有难度.为了做好讲评，取得较好的讲评效果，笔者进行了如下设计，特别是预设了一系列铺垫式问题.

问题1：大家读题后有哪些想法或解题念头？

预设：抛物线的对称轴为直线x=-，抛物线与x轴的两个公共点的坐标分别是（0，0）和（-b，0）.联立抛物线与直线的方程，可得关于x的方程x2+（b-1）x=0，计算根的判别式，结合b＞2，则可判定该方程一定有实数根，等等.教学时注意安排学生交流不同的想法，并追问其他学生是否理解，安排一些学困生复述（即再说一遍），有利于大家对问题的理解，便于后续问题的讨论.

问题2：让我们再深入解读条件b＞2，你们有哪些发现？

预设：当b＞2时，抛物线的对称轴一定在直线x=-1的左侧，抛物线与x轴的负半轴的交点一定在（-2，0）的左侧，抛物线与直线y=x的公共点坐标分别是（0，0）和（1-b，1-b）.

问题3：不妨取b=4，请同学们画出图像.

预设：如图1，画出图像，也可请学生到黑板上画出草图.

问题4：在图1中，在抛物线y=x2+4x上分别取点A、B，设它们关于直线y=x对称，连接AB交直线y=x于点C，这三个点有怎样的关系？能求出这三个点的坐标吗？

图1

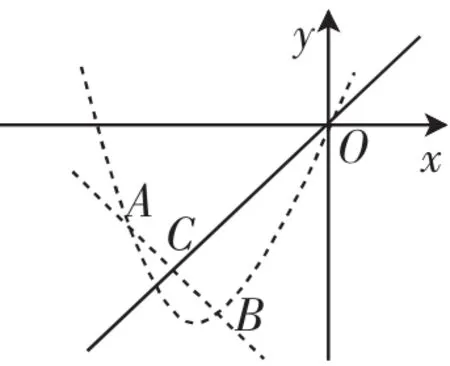
图2

预设：点C为AB的中点.如图1，直线AB与y=x交于点C，容易确认直线AB与y=x互相垂直，可设直线AB的解析式为y=-x+k.将y=-x+k与y=x2+4x联立，得关于x的方程x2+5x-k=0.根据根与系数的关系，知点A、B所对应的横坐标之和为-5.由点C是直线y=x、y=-x+k的交点，可解出点C的坐标为结合中点的性质，知k=-5，于是C点的坐标为（-2.5，-2.5），相应的，也可解出A、B两点的坐标.

问题5：现在我们可以“走向一般”，大家再尝试挑战一下考题吧.

预设：如图2，点C仍然为AB的中点.直线AB与y=x交于点C，容易确认直线AB与y=x互相垂直，可设直线AB的解析式为y=-x+k.将y=-x+k与y=x2+bx联立，得关于x的方程x2+（b+1）x-k=0.根据根与系数的关系，知点A、B所对应的横坐标之和为-（b+1）. 由点C是直线y=x、y=-x+k的交点，可解出点C的坐标为结合中点的性质，知k=-（b+1）.将其代入方程x2+（b+1）x-k=0，得x2+（b+1）x+（b+1）=0.接下来就是攻克当b为何值时，关于x的方程x2+（b+1）x+（b+1）=0有两个不相等的实数根.计算该方程的根的判别式，得不等式b2-2b-3＞0.学生可能又会出现一个障碍，不会解一元二次不等式，这时需要借助二次函数图像进行分析，求出b＜-1或b＞3，再结合原题条件b＞2可得出答案为b＞3.

组织这个环节教学时，注意发挥优秀学生的示范展示作用，在他们讲解思路之后，再请中等学生复述思路，让更多的学生理解，如果表达过程中有思维回路，可请其他学生参与评析、进行优化.

变式再练：

（1）若抛物线y=x2-3x上有两点M、N，它们恰关于直线y=x成轴对称，连接MN，交直线y=x于P点，求点P的坐标.

（2）若抛物线y=x2+bx（b＜-2）上存在关于直线y=-x成轴对称的两个点，分析b的取值范围.

改编意图：这两道习题针对上面的问题串而设计，可有效反馈学生对讲评过程中一些特殊化问题与一般化问题是否掌握.

二、解题教学要教学生学会思考

南京师范大学涂荣豹教授在新著中明确指出数学解题教学的任务，主要任务并不是让学生解题，而是通过解题与教学（学生解题、教师跟进的讲评这一全过程）来帮助学生“学解题”.以下就围绕解题教学如何教学生“学解题”、学会思考，提出笔者的一些做法和体会.

1.加强解题回顾与反思，深刻理解解法的关键步骤

教师解题研究不能止步于思路贯通、答案获得，而要在此基础上深入开展回顾与反思，包括对习题的一题多解、多解归一的研究，更进一步，还要深刻理解不同解法步骤中的关键步骤，学生的易错步骤，关键步骤是如何突破的.这些回顾与反思工作越深入，对于后续解题教学的设计帮助也就越大，否则后续解题教学设计常常缺少必要的铺垫式问题，不利于问题讲评时的渐次呈现，有些解法的出现就会如同“神仙下凡”，学生不太容易接受.像上文中考题的关键步骤有好几步，比如，构造恰当的草图分析；理解点C是线段AB的中点，以及由中点公式带来的它们的横坐标的关系式；由根的判别式得出的关于b的一元二次不等式的解集与取舍.

2.基于学情精心备课，预设铺垫式问题对话追问

教师在深刻理解习题的结构与关键步骤之后，还需要基于学情精心备课，即想清了“教什么”之后，需要结合“教谁”思考“怎么教”.具体来说，对于一些较难习题，并不能像参考答案一样渐次呈现所谓的“规范解答”，而要通过恰当的问题引导促进学生的思维参与“题”中，而不是教师主讲，很多学生（特别是学困生）却游离在讲评之外（无聊地装着在听课，其实什么都听不懂）.比如，上文考题讲评预设的“问题1”，这是一个开放式问题，目的就是让全体学生都参与进来，尽管都没有做出最终结果，但是每个人读完题目、理解题意后应该有些进展或解题念头，可以先在小组内交流，再全班交流，教师通过恰当的追问促进不同学生互评，深入解读根据题目条件能够推得的一些结论.另外，“问题4”也是一个典型的铺垫式问题，作为一种“特例引路”，让学生先经历常数系数的二次函数问题，然后过渡到含参二次函数问题，从“特殊”走向“一般”，不但能有效解决这道题，而且作为一种解法套路，启发学生在以后一些陌生问题的求解进程中加以运用.

3.变式再练反馈学情，贴近习题讲评的改编设问

在讲评之后，为了即时反馈学情，进行变式再练是有效的检查方式，这里要注意变式再练题的改编设计，一定要贴近习题讲评过程中涉及的解法或拓展的内容进行有针对性的变式改编，或者说变式改编题需要精心构思，确保“内容效度”的高度相关.上文考题讲评之后，我们给出的两道变式改编题分别针对考题讲评过程中的“问题4”“问题5”进行反馈检测，能有效评价学生对讲评内容的理解、掌握及运用情况.需要指出的是，开展变式再练这个教学环节得到很多老师的认可，但是这个环节的研发需要教师自觉修炼命题基本功，否则经过变式改编而成的习题出现错漏或表述不当反而不利于反馈学情.在这个意义上说，必要的命题能力应该是广大数学教师专业精进的一门必修课，需要认真钻研.

三、写在后面

学习数学离不开解题，数学教学离不开解题教学.解题教学的品质与深度是值得研究的现实话题，它虽然不是高大上的课题，却是最接地气的草根课题，应该成为广大一线教师的“自觉”课题.希望我们在上文中结合案例给出的一些思考和建议能够抛砖引玉，看到更多围绕解题教学的深度思考与实践案例，丰富我们对高品质解题教学的认识与理解.