基于概率Budyko方程的流域未来可用水资源比例预估

陈泽峰，王卫光，李长妮，丁一民，傅健宇

(1.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学水文水资源学院，南京 210098；3.陕西省河流工程技术研究中心，西安 710018)

近年来，伴随着全球变暖和人类活动的影响，降水、陆面蒸散发、流域下垫面、大气化学组分等均发生显著变化[1,2]，进而影响水文循环过程[3]，使得流域径流过程发生改变[4]、极端水文事件频繁发生，也加剧了我国水资源短缺、供需矛盾突出、水环境恶化等的水资源状况。因此，精确的评估陆面可利用水资源量变得至关重要。

Budyko水热耦合平衡方程[5,6]由于物理机制明确、输入资料少，因此在大时间尺度上可利用水资源量的评估和预测工作中得到了广泛的应用[7,8]。Budyko理论最初是表示多年平均蒸发率(实际蒸散发AET/降水P)和干旱指数(潜在蒸散发PET/降水P)关系的无参数方程。随后，为了刻画不同下垫面特征的流域Budyko曲线形状，含有参数ω的Budyko方程被逐渐发展起来。含参数的Budyko方程对Budyko曲线的拟合精度较高，也因此应用较为广泛。虽然，众多学者研究过参数ω与单个或多个流域要素间的关系[7,9]，但由于参数ω与观测变量间的关系复杂，对于不同气候状况、不同流域的ω和各因素间关系的系统变化仍然没有一个确定的结论。对此，Greve等[10]用美国流域的观测数据，建立了从理论上评估不同流域特征可用水资源量的概率Budyko方程。随后，基于上述理论，Wang和Fu[11]结合流域下垫面特征，改进了概率Budyko方程，提出了双变量概率性Budyko框架，提高了可利用水资源量的准确性。概率Budyko的发展，为评估相同气候条件下，不同下垫面特征的流域可用水资源及其不确定性提供了新的视角。将基于下垫面因素的参数ω的概率分布代入Budyko方程，可以定量评估未来水资源预估的不确定性，从而为水资源管理者和决策者提供更精确的依据。

本文结合IPCC 第五次报告 CMIP5 的气候模式数据(CanESM2)，运用统计降尺度方法，预估我国不同干湿特征的4个典型流域(黑河流域、滦河山区、汉江丹江口以上流域和赣江栋背以上流域)未来水文气象变量，分析其变化特征；同时，基于构建的双变量概率性Budyko方程，预估典型流域不同排放情景下未来可用水资源比率的分布，并评估其不确定性。

1 流域概况及资料

本文选取4个典型流域(黑河流域、滦河山区、汉江丹江口以上流域和赣江栋背以上流域)为研究区域。4个流域具有不同的干湿特征：黑河流域代表干旱流域、滦河山区代表半干旱流域、汉江丹江口以上流域代表半湿润流域、赣江栋背以上流域代表湿润流域。研究区位置及气象站点分布情况如图1所示。

图1 4个典型流域及其气象站点的分布Fig.1 Spatial distribution of four typical catchments and locations of meteorological stations

研究区历史观测数据包括从国家气象局(http:∥cdc.cma.gov.cn/)搜集的4个流域内共21个气象站点1961-2000年间逐日降水、最低气温、最高气温、日照时数、平均相对湿度和平均风速资料。潜在蒸散发通过具有明确物理机制的Penman-Monteith方法[12]计算。各流域上降水、潜在蒸散发通过泰森多边形法[13]计算流域内部气象站点的面积权重来得到。

未来数据本文选择IPCC 第五次报告 CMIP5 的CanESM2(the second generation of Canadian Earth System Model)气候模式网格数据，CanESM2气候模式由加拿大环境气候变化部门的气候模型和分析中心提供，其空间分辨率为2.812 5°×2.812 5°，时间序列为2006-2100年。CanESM2气候模式包括3个排放情景，分别是RCP 26、RCP 45和RCP 85，依次描述的是低排放情景，中等排放情景和高排放情景。

再分析资料(NCEP，National Centers for Environmental prediction)同样来自加拿大环境气候变化部门的气候模型和分析中心。该NCEP数据集的时间长度是1961-2005年，空间尺度与CanESM2气候模式相同(2.812 5°×2.812 5°)。NCEP数据包括26个大气因子，主要用来率定和验证统计降尺度模型，以预测未来不同排放情景下的气候变量。

2 研究方法

2.1 概率Budyko方程

1981年，傅抱璞[14]在Budyko假设的基础上，根据流域水文气候的物理机制，经过量纲分析和数学推导，得到了Budyko假设的首个解析表达式：

(1)

式中：ω为表征流域自然地理特性的无量纲参数，且ω≥1。

由于傅抱璞公式的推导过程为Budyko假设提供了数理基础，具有物理和数学意义，所以与其他经验的Budyko方程相比，傅抱璞公式的认可程度较高并且应用较为广泛。

相比于传统的Budyko方程给定一个干旱指数值只能得到一个蒸发率，概率Budyko方程通过建立参数ω的概率分布得到的是蒸发率的一个分布，继而可以定量评估相同气候条件下，不同下垫面特征流域可利用水资源量的不确定性。

本文以傅抱璞的Budyko水热耦合平衡方程为依据，通过Copula函数，构造Budyko方程参数ω与流域下垫面因素(植被覆盖指数、土壤可用含水量、土壤容重、流域高程、坡度、复合地形指数)的边缘分布函数。经过参数计算、拟合优度评价等选取最优的Copula函数，分别建立ω和各因素的联合分布函数，以植被覆盖指数(NDVI)为例，联合概率分布见图2。随后，计算ω在流域下垫面条件下的条件分布函数，反推出在下垫面各因素限制后的参数ω，进而构建基于流域下垫面特征的概率Budyko方程。具体方法见Wang和Fu[11]。

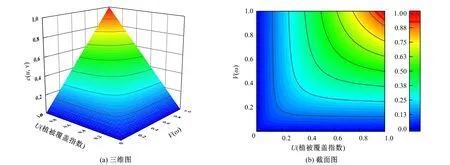
图2 参数ω与植被覆盖指数的联合概率分布图Fig.2 Joint probability distribution of ω and NDVI

2.2 统计降尺度模型SDSM

统计降尺度(Statistical Downscaling Model)的核心是建立大尺度气候因子与站点观测变量之间的关系。由于运行速度快且成本低，统计降尺度相比动力降尺度成为众多学者首选的方法[15]，也因此被广泛应用于评估气候变化背景下气象、水文、环境等的响应[16,17]。

统计降尺度的主要过程可分为以下4步：预测因子的筛选；构建模型；模型的率定和验证；未来气象变量的预测。

3 结果与分析

3.1 统计降尺度模型的率定与验证

预测因子的筛选是统计降尺度的核心环节，主要依据观测变量和多个再分析大气因子间的相关性和偏相关性，从而筛选出最相关的预测因子。本文计算了4个典型流域日尺度的潜在蒸散发与降水和26个气候因子间的相关系数(corr)和偏相关系数(p-corr)，并从中选取最相关的预报因子。

因子筛选之后，进行模型计算和率定验证。本文以1961-1990年作为模型率定期，1991-2000年为模型验证期，用相关系数R、模拟值标准差与观测值标准差的比值RS、确定性系数Ens和偏差Bias4个指标来评价模型，以滦河山区的6个气象站点为例，评价结果见表1。

可以看出，模型对潜在蒸散发的模拟效果较好，R和RS在率定期和验证期均超过了0.92，多伦站和青龙站的RS甚至等于1；确定性系数Ens也都大于0.80；偏差Bias大都接近于0。降水的模拟结果虽然不如潜在蒸散发好，但R都在0.43以上，RS都大于0.57，也能用来预估未来的气象变量。

流域尺度上，比较了验证期(1991-2000年)实测月潜在蒸散发和模拟月潜在蒸散发。黑河流域、滦河山区、汉江丹江口以上流域和赣江栋背以上流域的R2分别达到0.993、0.992、0.977和0.975，说明整体模拟效果好。同时比较了验证期(1991-2000年)实测月降水和模拟月降水。黑河流域、滦河山区、汉江丹江口以上流域和赣江栋背以上流域的R2分别达到0.800、0.912、0.811和0.812，4个流域的R2都大于0.80，说明模拟效果较好。总之，SDSM在构建降水和潜在蒸散发时具有良好的模拟效果，可用于对未来数据进行降尺度。

3.2 流域未来水文气象变量的预估

根据建立好的SDSM，输入不同排放情景的预报因子，便可得到未来不同情景下的日潜在蒸散发量和日降水量，进而累加计算得到年潜在蒸散发量和降水量，其结果如图3所示。4个流域的潜在蒸散发量在未来RCP 26、RCP 45和RCP 85情景下均呈上升趋势，且RCP 85情景下的增加趋势更为明显，尤其在2050年之后。降水的整体增加趋势相对较小，尤其在湿润的赣江栋背以上流域。

4个流域未来时段2021-2050年3个排放情景的多年平均降水量(P)和潜在蒸散发量(PET)，继而计算得到相应的干旱指数(AI)。结果表明，在RCP26情景下，黑河流域、滦河山区、汉江丹江口以上流域以及赣江栋背以上流域的AI分别为8.944、1.651、1.144和0.884；在RCP45情景下，黑河流域、滦河山区、汉江丹江口以上流域以及赣江栋背以上流域的AI分别为8.797、1.727、1.145和0.867；在RCP85情景下，黑河流域、滦河山区、汉江丹江口以上流域以及赣江栋背以上流域的AI分别为8.745、1.710、1.131和0.879。

表1 统计降尺度模型在构建滦河山区各气象站点日潜在蒸散发和日降水时的模拟结果评价Tab.1 Evaluation of daily potential evapotranspiration and precipitation at each at each meteorological station of Luanhe Mountain that simulated by statistical downscaling model

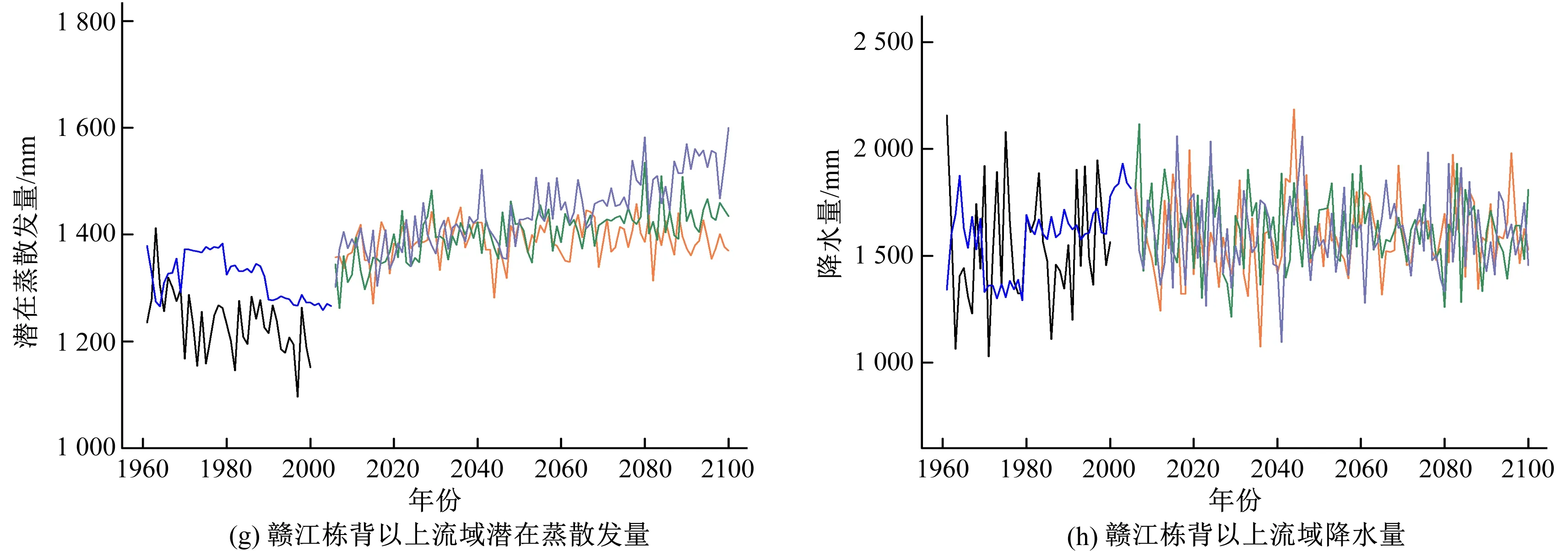
图3 流域历史实测潜在蒸散发、降水和CanESM2模式不同气候情景下的潜在蒸散发、降水Fig.3 Measured potential evapotranspiration and the potential evapotranspiration under the different emission scenarios based on CanESM2 for four catchments

3.3 流域2021-2050年可用水资源比率的预估

在构建概率Budyko方程的过程中，通过对比下垫面各因素限制后的参数ω′和ω的概率密度函数，得到了各下垫面因素对参数ω的影响程度。结果表明，黑河流域和赣江栋背以上流域的最大影响因素为植被覆盖指数，汉江丹江口以上流域的最大影响因素为土壤可用含水量，而滦河山区的最大影响因素为高程。因此，根据建立的概率Budyko方程，假定流域2021-2050年参数ω分布与历史时期(1982-2008年)ω的分布保持一致，即黑河流域和赣江栋背以上流域的参数是植被覆盖指数限定后的ω′，滦河山区和汉江丹江口以上流域的参数分别是由高程和土壤可用含水量限定后的ω′。将4个典型流域对应的ω′及得到的未来不同排放情景下干旱指数(AI)分别代入Budyko方程，便可得到未来可用水资源比率的分布，从而评估其不确定性。

图4展示了4个流域不同排放情景下2021-2050年多年平均可用水资源比率的分布。可发现，黑河流域可用水资源比率值分布范围较窄，多在0～0.06之间，不同排放情景的可用水资源比率值较为接近[图4(a)]。滦河山区可用水资源比率范围相对较宽，多集中在0～0.5之间，且有双峰现象，说明有两段值出现的频率较大，0.1～0.25、0.25～0.4为两个双峰的大概位置；RCP 26 情景与另外两个排放情景下的可用水资源比率略有差异[图4(b)]。汉江丹江口以上流域可用水资源比率大都集中在0.2～0.6间，双峰现象略不明显，不同排放情景的可用水资源比率值较为接近[图4(c)]。赣江栋背以上流域可用水资源比率多分布在0.3～0.8的范围内，双峰现象明显，且在峰值以前的曲线斜率相对峰值以后的曲线斜率较小，不同排放情景的可用水资源比率值差异较小[图4(d)]。

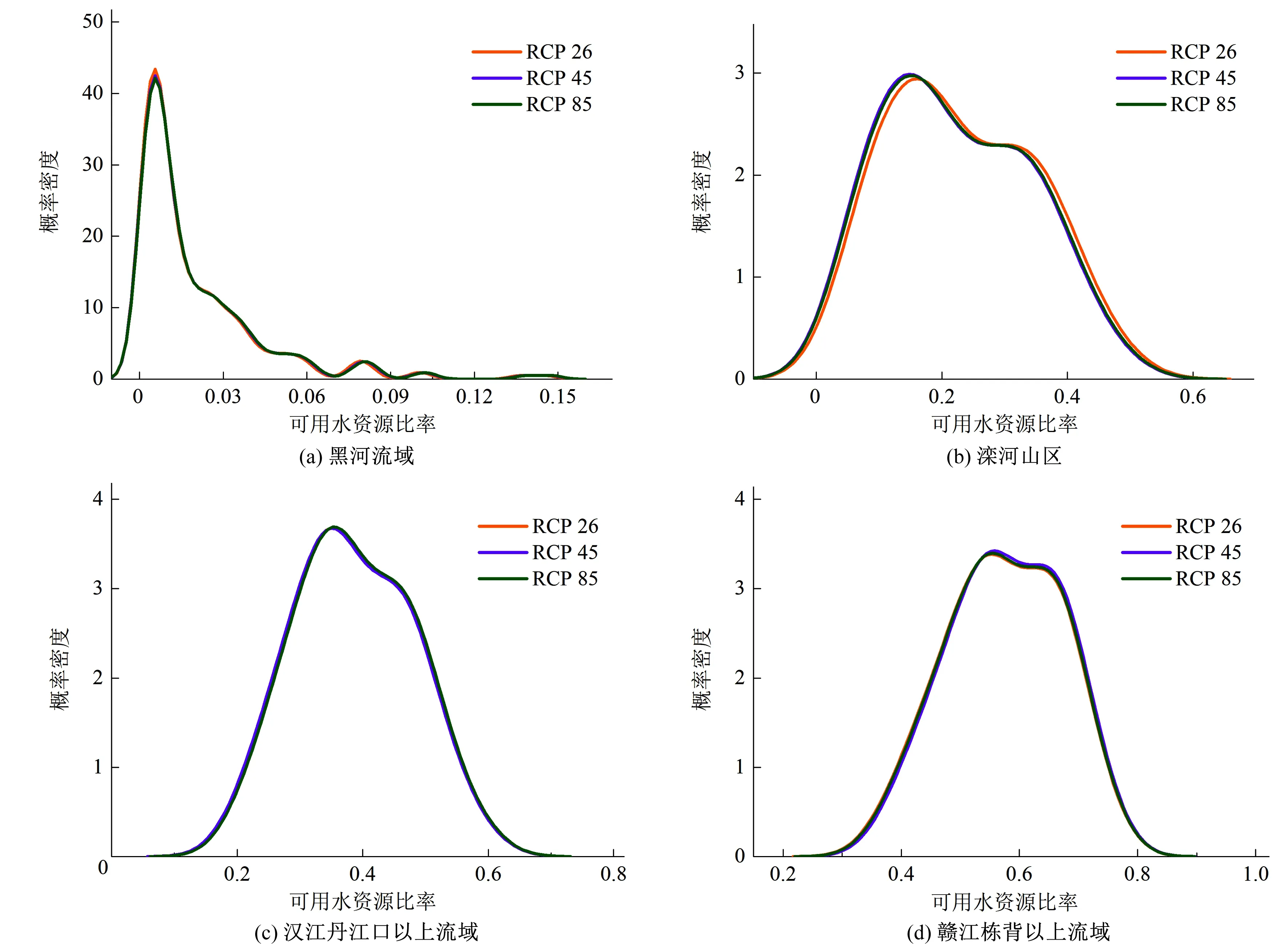
图4 流域2021-2050年不同排放情景下可用水资源比率的分布Fig.4 Water availability ratio under the different emission scenarios during 2021-2050 for four catchments

从可用水资源比率的箱线图(图5)可看出，各流域可用水资源比率在不同排放情景下的分布极为相似，表明不同的排放情景对可用水资源比率的影响不大；与常理一致，可用水资源比率值随着流域湿润程度的增加而增加，黑河流域、滦河山区、汉江丹江口以上流域和赣江栋背以上流域可用水资源比率的中位数依次为0.10、0.20、0.38和0.57；箱子的高度(即四分位距IQR)在黑河流域最矮(0.022)，汉江丹江口以上流域次之(0.144)，接着是赣江栋背以上流域(0.151)，滦河山区最高(0.194)，说明可用水资源比率的不确定性在滦河山区最大，黑河流域最小，其余两个流域介于之间。此外，黑河流域和赣江栋背以上流域的下垫面最大影响因素同为植被覆盖指数，两个流域的Budyko参数均为由植被覆盖指数限定之后的参数ω，但其可用水资源比率的大小及不确定性却相差甚大，说明流域气候特征对流域水资源状况影响强烈，且加入植被覆盖指数后可用水资源比率的不确定性在干旱区域(黑河流域)比湿润区域(赣江栋背以上流域)小。

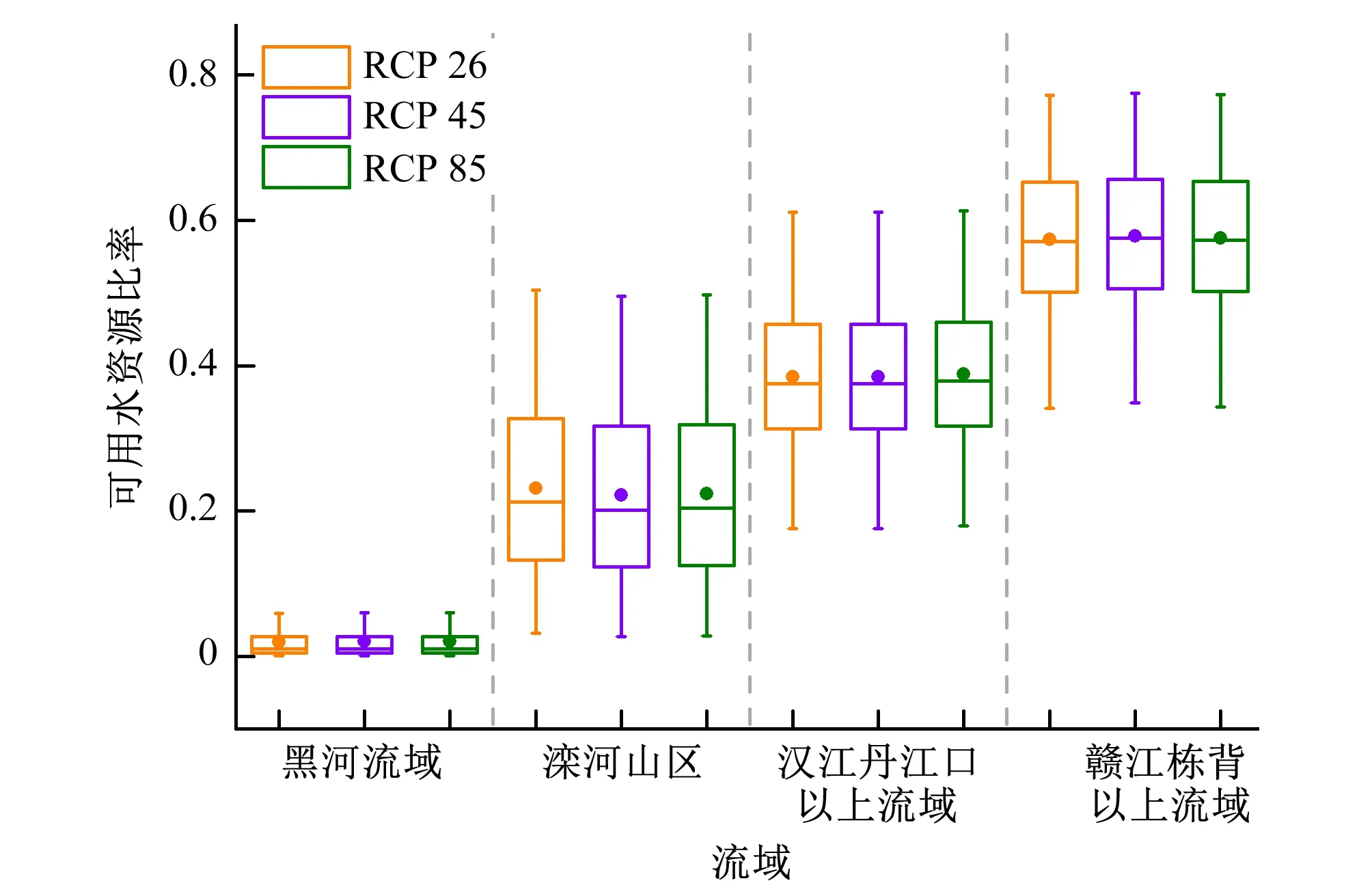
箱子最底端和最顶端的短线分别表示可用水资源比率的最小值和最大值，箱子从下往上的三条线依次表示25%、50%、75%处的值，实心圆代表可用水资源比率的平均值图5 流域2021-2050年不同排放情景下可用水资源比率的箱线图Fig. 5 Boxplot of water availability ratio under the different emission scenarios during 2021-2050 for four catchments

总之，不同排放情景对流域可用水资源比率的影响较小，流域可用水资源比率值随着流域湿润程度的增加而增加，可用水资源比率的不确定性从高到低依次是滦河山区、赣江栋背以上流域、汉江丹江口以上流域和黑河流域。此外，湿润区赣江栋背以上流域的可用水资源比率的不确定性略高于半湿润区汉江丹江口以上流域的这一结果也反映出研究不同下垫面因素对参数ω影响程度的必要性。

4 结 语

本文运用统计降尺度模型(SDSM)，结合CanESM2气候模式、实测降水、由Penman-Monteith公式计算的潜在蒸散发，预估未来3种不同辐射强迫和大气排放标准(RCP 26、RCP 45、RCP 85)下的降水量和潜在蒸散发量；基于构建的双变量概率Budyko方程，对我国不同干旱特征的典型流域(黑河流域、滦河山区、汉江丹江口以上流域和赣江栋背以上流域)未来可用水资源比率进行预估，并分析其不确定性。主要结果如下：

(1)4个典型流域的潜在蒸散发量在未来RCP 26、RCP 45和RCP 85情景下均呈上升趋势，且在2050年之后，RCP 85情景下的潜在蒸散发量最大，RCP 45情景下的潜在蒸散发量次之，RCP 26情景下的潜在蒸散发量最小；降水的整体增加趋势则相对较小，尤其在湿润的赣江栋背以上流域。

(2)黑河流域、滦河山区、汉江丹江口以上流域和赣江栋背以上流域可用水资源比率的中位数依次为0.10、0.20、0.38和0.57，即4个流域2021-2050年多年平均可用水资源比率值随着湿润程度的增加而增加；不同排放情景下的可用水资源比率分布的差异较小；滦河山区和赣江栋背以上流域的可用水资源比率分布有双峰现象。

(3)不同排放情景对流域可用水资源比率的不确定性影响较小；4个流域可用水资源比率的不确定性从高到低依次是滦河山区(IQR为0.194)、赣江栋背以上流域(IQR为0.151)、汉江丹江口以上流域(IQR为0.144)和黑河流域(IQR为0.022)。