基于LFM信号的TDMA网络精密时间同步方法
2019-06-25王天雄陈仕进张玉鹏闫胜虎
王天雄,陈仕进,张玉鹏,闫胜虎
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
时间同步是时分多址(TDMA)网络正常运行的基础,网内各个节点的时间同步精度达到微秒量级,即可保证节点间的无碰撞同步信息传输,常用的时间同步算法均能满足需求,例如:参考广播方法[1]、RTT时间同步算法[2-3]和PTP时间同步算法[4]。文献[5-6]针对自组织网络研究了分布式同步算法,虽然时间同步精度不高,但是无需中心节点,网络抗毁性能高。若要利用TDMA数据链路进行节点间的测距,则需要提高网内时间同步精度,例如:30 m的测距误差就要求时间同步精度达到100 ns以内。为了提高时间同步精度,文献[7]设计了基于卡尔曼滤波的高精度RTT时间同步算法,将时间同步误差控制在50 ns以下。文献[8]将卡尔曼滤波和RTT-PTP算法相结合,在Link22数据链结构的基础上降低了时间偏差率误差。
随着多战斗单元协同作战理论和体系的发展,数据链路的时间同步面临着更严峻的挑战。例如:战斗单元执行协同探测、协同侦查等任务时需要各个战斗单元间纳秒级的时间同步[9-11],而卫星导航信号一旦被干扰,外部时钟源无法进行授时,这就需要靠数据链路完成纳秒级的精密时间同步,为其他作战载荷提供时统,支撑协同作战任务。
本文通过研究TDMA网络的RTT同步技术,分析同步误差产生的原因。设计了基于线性调频(LFM)脉冲的时间同步算法,利用LFM脉冲压缩的抗多普勒优势[12-13],通过采用大时间带宽积的LFM脉冲提高了时隙到达时间的估计精度。仿真和实际平台验证表明该算法行之有效。
1 RTT同步技术
RTT时间同步方法是通过测量网络内节点之间的信号往返时间来估计时间同步误差的。在估计时间误差的同时,还能够估计出节点间的信号传输时延,因此,常用于TDMA网络的节点间测距。
RTT时间同步原理如图1所示。其中,tm为主节点(时钟参考节点)时间,tc为从节点时间,Δt为主从节点的时钟误差。通过RTT算法可以将时间tc与时间tm同步。
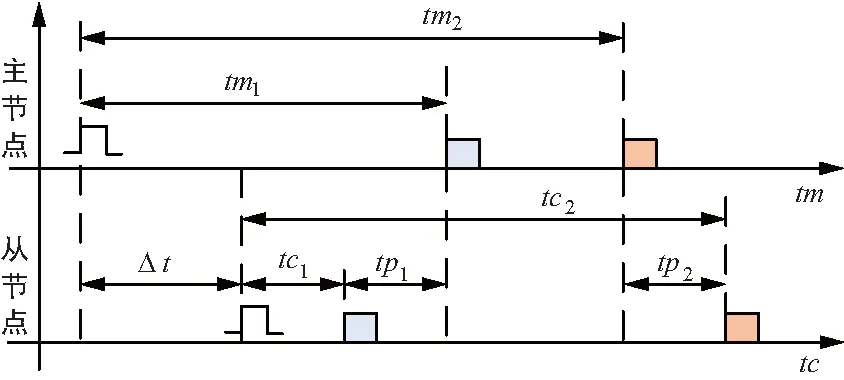
图1 RTT时间同步原理
从节点在其本地时间tc1时发送RTT询问时隙,主节点在其本地时间tm1时收到来自从节点的RTT询问时隙,时隙传输时延为tp1。主节点在其本地时间tm2发送RTT应答时隙,从节点在其本地时间tc2时收到来自主节点的RTT应答时隙,时隙传输时延为tp2。
假设主从节点交互时隙的时间非常短,主从节点间的距离可以近似认为不变,即可以取tp1=tp2=tp,此时,以上各参数满足以下方程:
(1)
从而有:
Δt=(tm1+tm2-tc1-tc2)/2,
(2)
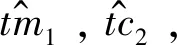
(3)
分析上述RTT时间误差估计流程可以看出,在不考虑硬件一致性等原因引起的系统误差的前提下,仅从算法本身考虑,主要存在以下估计误差:在估计tm1,tc2的时候存在估计误差εm,εs;由主从节点的时钟相对漂移引入的随机误差εc;主从节点交互脉冲时由于主从节点的相对位置变化会引起tp1≠tp2,因此会造成产生估计误差εtp。
目前减小上述误差的途径主要有3条:在硬件上提高用作系统时钟的晶振稳定度,减小εc的方差;在软件上使用卡尔曼滤波等估计算法,减小由εc,εm,εs引起的估计误差方差;在帧结构设计上,尽量减小主从节点的时隙交互时间,减小由εtp引起的估计误差。
然而,由于εm,εs的方差较大,即使采用了相应的估计算法,时间同步误差也只能控制在几十纳秒量级。要想进一步提高时间同步精度,需要从根本上减小εm,εs的方差。当信号带宽受限时,增加信号持续时间、提高信号的时间带宽积是提高信号到达时间估计精度的有效手段。对于常规的伪随机序列调制信号,提高信号持续时间就意味着增加序列码长。但在多普勒频偏条件下,对伪随机序列进行长码匹配滤波,其累积能量损失会随着其码长的增加而增大,累积能量信噪比的降低直接影响信号的捕获概率和到达时间的估计准确度[14-16]。若采用差分能量累积算法,则会额外损失信噪比,要想达到与相干能量累积相同的效果,需要进一步加长伪随机序列,增加额外时间开销。若采用分段匹配加FFT的能量累积算法,额外信噪比损失较小,但会大大增加系统的复杂度,且原有的时域一维峰值搜索将变为时频二维峰值搜索,增加了算法的复杂度。因此,采用伪随机长码序列调制信号进行信号到达时间估计存在很大的局限性。
线性调频信号(LFM)对多普勒频偏有天然的抗性,文献[17-18]指出,通过脉冲压缩方法对LFM信号进行能量累积时,由多普勒频偏引起的能量损失只与频偏带宽比有关,与信号持续时间无关。因此,可以对大时间带宽积的LFM信号直接进行脉冲压缩,并利用能量峰值位置准确估计脉冲到达时间,算法复杂度和实现复杂度均较低。
2 LFM信号原理
2.1 LFM信号的脉冲压缩
线性调频信号可以表示为:
(4)
式中,A为幅度,f0为初始频率,k为调频率。设线性调频信号的持续时间为τ,其理想的时频分布如图2所示。
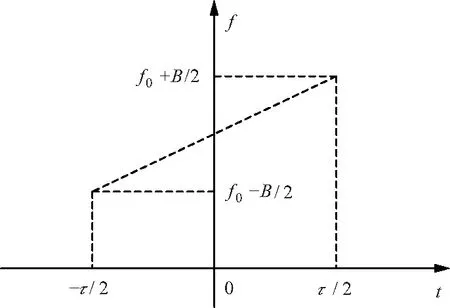
图2 线性调频信号的理想时频分布
从图2中能够看出,线性调频信号的时宽为T=τ,其频率随时间线性变化,因此是非平稳信号,其瞬时频率为:
f=f0+kt。
(5)
脉冲压缩是雷达术语,在通信领域,即为匹配滤波。因此,LFM脉冲的捕获和到达时间估计,是通过搜索信号匹配滤波响应峰值来实现的[12]。
2.2 LFM信号脉压抗多普勒原理
线性调频信号对多普勒频移不敏感,在较大多普勒频移的情况下,仍能通过匹配滤波得到很好的能量累积,但匹配滤波器响应会产生附加时延,延时的大小正比于多普勒频移,延时会使脉冲到达时间的估计产生误差。
LFM多普勒频移影响示意图如图3所示。LFM脉冲附加了多普勒频移之后,相对于原有频率附加了频率fd。实线部分为原始频率变化范围,虚线部分为频移后的频率变化范围,因为只有频率在f1~f2部分的波形可以通过脉冲压缩收集能量,所以引入多普勒频移后,将会产生以下不利影响:
① 可压缩段变小了,将会损失一定的累积能量,损失部分可以表示为Δtd/T;
② 匹配滤波器输出响应产生附加时延Δtd=Tfd/(f1-f2)。
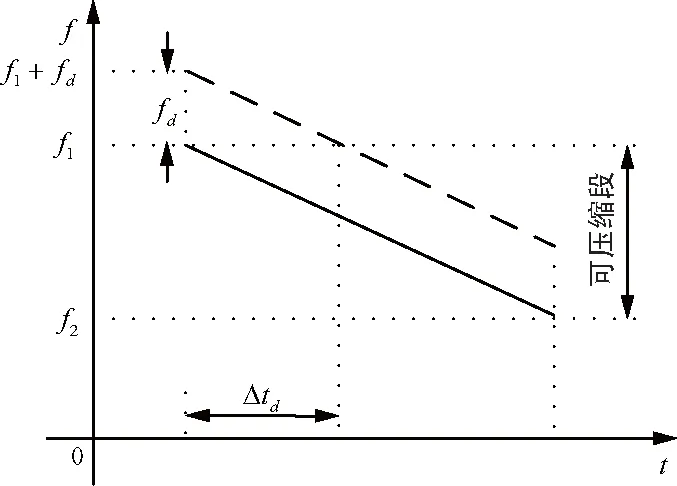
图3 LFM多普勒频移影响示意图
通过上述分析可知,当实际的多普勒频移与LFM信号带宽比较小时,产生的能量损失可以忽略不计。但产生的附加时延必需予以补偿。正负斜率脉冲多普勒补偿算法可以有效地修正附加时延。
正负斜率脉冲补偿算法要求发送端连续发送正斜率脉冲和负斜率脉冲2个LFM脉冲,即2个脉冲信号的调频斜率幅值相等,方向相反。在接收端需要2个匹配滤波器分别匹配正斜率脉冲和负斜率脉冲。当发射正斜率脉冲时,多普勒频移使脉压后的波形包络在时间轴上发生移动,偏移量为Δtd1=-2πfd/k。同理,发射负斜率脉冲时,多普勒频移使脉压后的波形包络在时间轴上发生移动,偏移量为Δtd2=2πfd/k,其原理如图4所示。
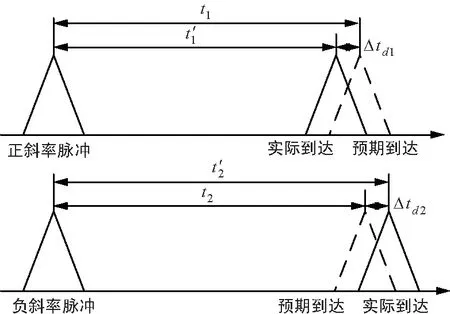
图4 多普勒对LFM正负斜率脉冲的影响
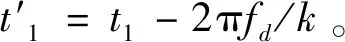
3 基于LFM的TDMA网络时间同步方法
3.1 TDMA网络帧结构
为了利用LFM脉冲进行信号到达时间估计的优势。TDMA网络时帧结构如图5所示。一个时帧被分为2部分,前半部分为LFM脉冲部分,用于节点间进行信号往返时间估计,每个节点发送一个LFM脉冲串#n′,每个脉冲串包含若干个正负斜率脉冲对;后半部分为通信波形部分,用于节点间进行正常通信和传输LFM脉冲串到达时间的估计结果。

图5 系统时帧结构图
将LFM脉冲集中设计在时帧的前区,是为了尽可能地减小节点间信号往返交互的时间,从而减小误差εtp的影响。
3.2 TDMA网络时间同步流程
基于上述时帧结构,主从节点工作流程如图6所示。

图6 主从节点工作流程
主节点流程描述为:
① 系统初始化后,在tm=0时产生帧起始脉冲,为通信时隙和LFM脉冲时隙提供时间基准;
③ 在tm为tm2时发送RTT应答脉冲串;
由于LFM脉冲串本身没有调制信息,因此,从LFM信号本身无法区分脉冲的信源,所以,在主从节点时间不同步时,从节点无法辨认主节点发送的LFM脉冲串,也就无法进行时间的初始化校准。为了克服上述问题,从节点借助通信时隙来完成时间的初始化校准,因此,从节点的时间同步分为时间粗同步和时间细同步2个步骤。
在时间粗同步阶段,从节点工作流程描述为:
① 系统初始化后从节点保持静默,接收主节点通信时隙,从中恢复时间的粗定时;
② 在粗同步的时间下,根据脉冲串到达时间区分脉冲串的信源,并进行本节点各LFM脉冲时隙和通信时隙的发送。
在时间细同步阶段,从节点工作流程描述为:
① 在tc=0时产生帧起始脉冲,为通信时隙和LFM脉冲调制提供时间基准;
② 在tc为tc1时发送RTT询问脉冲串;
⑤ 按式(3)计算Δt,并修正本地时间;
4 仿真和实现验证
本文针对上述TDMA网络时间同步方法,以4节点网络进行了仿真和实现验证。
仿真条件1:校时帧周期为40 ms,其中LFM脉冲部分占3 ms,通信波形部分占37 ms,每个LFM脉冲串包含8个正负斜率脉冲对,每个脉冲脉宽40 μs;信号带宽20 MHz;多普勒频偏20 kHz;系统时钟晶振稳定度10-8;节点相对运动速度不大于30 m/s。主从节点的时间同步误差如图7所示。
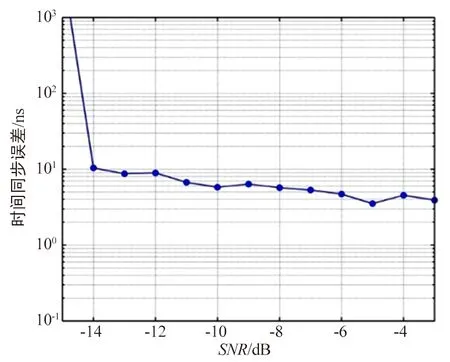
图7 条件1下主从节点的同步误差图
从图7可以看出,在接收信噪比达到-14 dB时,时间同步误差开始收敛,当信噪比达到-8 dB时,同步误差标准差不大于5.5 ns。
仿真条件2:在条件1的基础上分别将LFM脉冲带宽和脉冲宽度降低到10 MHz,20 μs,仿真结果如图8所示。从图8可以看出,由于降低LFM的带宽或脉宽减小了脉冲的时间带宽积,致使时间同步灵敏度下降,-8 dB时,时间同步误差标准差增大到10 ns左右。
仿真条件3:在仿真条件1的基础上将多普勒频偏增加到200 kHz,仿真结果如图9所示。
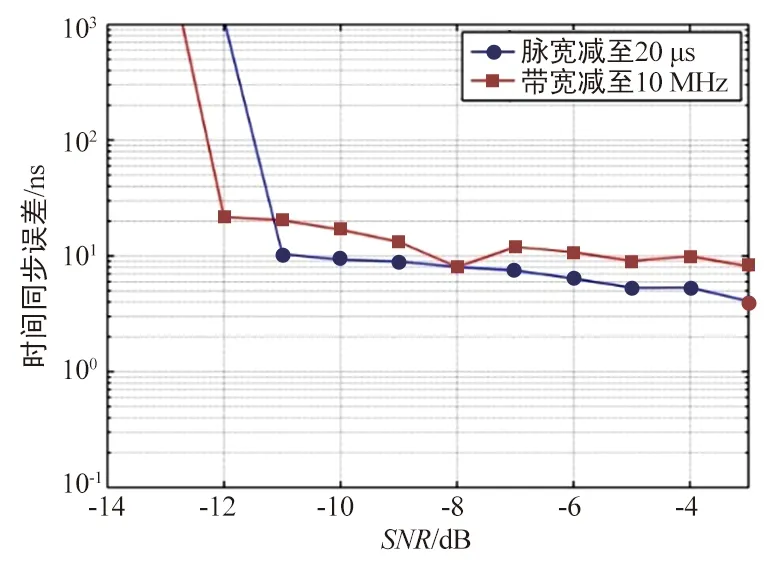
图8 条件2下主从节点时间同步误差图
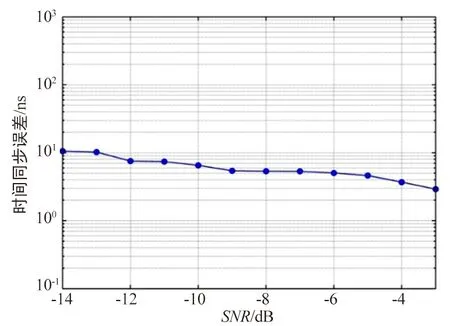
图9 条件3下主从节点时间同步误差图
比较图7和图9可知,LFM信号具有良好的抗多普勒性能,在200 kHz多普勒频偏下,时间同步灵敏度和时间同步精度均未有明显的损失。
仿真条件4:在条件1的基础上分别将时钟稳定度调制为10-7,节点间相对运动速度调整为300 m/s,校时帧周期调整为1 s,仿真结果如图10所示。
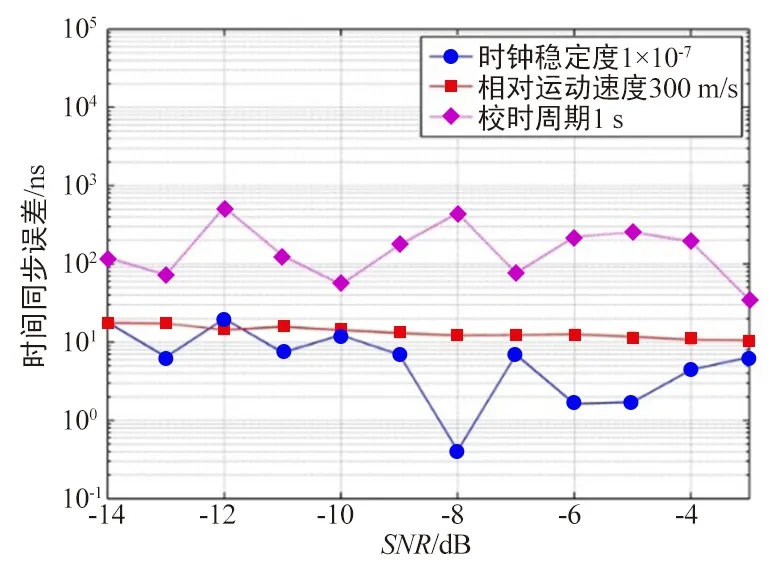
图10 条件4下主从节点时间同步误差图
从图10可以看出,时钟稳定度、相对运动速度和校时帧周期直接影响时间同步精度,为了减小时间同步精度损失,应选用高稳定度的时钟和减小校时周期。
根据上述方法设计FPGA程序实现,并加载到现有的通信终端设备上,实验条件是仿真条件1的基础上去掉节点间的相对运动速度,利用示波器来观察实际的主从节点帧起始脉冲的同步情况。
实验结果显示,从节点的帧起始脉冲在主节点帧起始脉冲附近波动,误差介于±4 ns左右之间,因为没有模拟节点间的相对运动,所以实测结果要好于仿真结果。
5 结束语
本文利用LFM信号抗多普勒性能强的特点,基于LFM信号设计了TDMA网络的RTT时间同步算法。LFM信号的高时间带宽积提高了接收端脉冲压缩的能量累积量,减小了脉冲到达时间的估计误差;节点间集中交互LFM脉冲的帧结构,减小了脉冲交互时间,降低了节点间相对运动引入的时间同步误差。仿真和实际平台验证结果表明,该方法在大多普勒频移环境下仍能够大幅提高TDMA网络内节点的时间同步精度,可以为其他任务载荷提供高精度授时,特别适用于小规模协同作战。
