坐标测量法在机载设备安装定位中的应用

2019-06-25许志林彭金京

教练机 2019年1期

许志林，彭金京

（1.中电科芜湖通用航空产业技术研究院有限公司，安徽芜湖，241000；2.航空工业洪都，江西南昌，330024）

0 引言

用于测量飞机姿态、速度、加速度、空速等信息的设备在飞机上进行安装的过程中，设备的测量轴需要与机体的相应轴线平行，对于无人机或电传飞机，其安装精度要求更高，因此，在实际安装过程中，需要有可靠、精确的检测方法，对设备安装情况进行测量。

一般飞机在设计之初会考虑通过型架、模具等，在机体上布置对应的安装平台，提供尽可能高精度的安装定位。传统的金属类飞机由于有工装型架，可通过型架预设置高精度的安装平台，后续再通过工程方法检验一下即可，而对于复合材料飞机或临时改装的飞机，在设计之初未考虑相关的定位参考时，会带来较大的安装难题。

但即使是通过型架预设置的安装平台，如果采用可信度较高的检测方法在设备安装后再次进行复检，可为设备的准确安装提供更加可靠的保障。

本文介绍一种在设备安装后对其定位情况进行检测分析的方法，通过在飞机和设备上分别引出与其轴线有相对关系的测量点，利用全站仪建立当前飞机状态的空间坐标系，测量各参考基准点的坐标，再利用三维软件CATIA将坐标进行空间还原，借用辅助线和平面来计算设备轴线与飞机轴线的相对误差，以分析安装定位要求是否满足设计需要。

本文中的全站仪也可使用其他可测量坐标点的设备代替，三维软件CATIA也可用AuToCAD或UG等软件代替。

1 坐标测量方法的基本原理

以惯性导航设备为例，惯性导航设备是利用惯性测量元件测量机载设备相对惯性空间的运动参数，机载设备本身一般具备三个测量轴，内部的加速度计和陀螺仪分别用于测量飞机的纵、横、航向的线加速度和角速度。为保证惯性导航设备能够准确测量飞机的姿态信息，设备在安装时，要求设备的测量轴与飞机的轴线尽可能的平行，且有相应的精度要求。

坐标测量方法通过分别测量设备和飞机上的基准面或基准轴线上的某些测量点的坐标值，再通过坐标点连线、引垂线、作铅垂面等方法，在虚拟三维空间中将基准面、基准线进行还原，利用三维软件的测量模块对安装误差进行计算分析。其实施步骤如图1所示。

图1 坐标测量方法和步骤

2 某型机惯导设备安装方法介绍

2.1 安装前的准备

惯导设备一般配置有过渡安装板，在安装设备前先保证安装板的安装精度，再将惯导设备直接安装于过渡安装板上即可。安装前，先放置好全站仪和飞机的相对位置，全站仪应放置在飞机的侧边，偏离飞机对称线一定的距离，同时与飞机也应保持一定的距离，以减小测量误差对测量精度的影响，如图2所示，建议全站仪距离机头的航向距离不小于10m，距离飞机对称面的距离不小于4m。分别将飞机和全站仪调成水平状态，然后将过渡板安装于安装面上，通过加垫等方法将安装板调整为水平状态。

在准备测量的飞机和设备的基准点上分别做好标识记号，如果被测量设备位于全站仪难以观察处，可通过增加工装将相对测量基准引出至可观察位置。本例中的被测量设备位于座舱内部，全站仪无法观测到的位置，设计制作了一工字型工装将基准面抬高至可观测位置，进行间接测量。

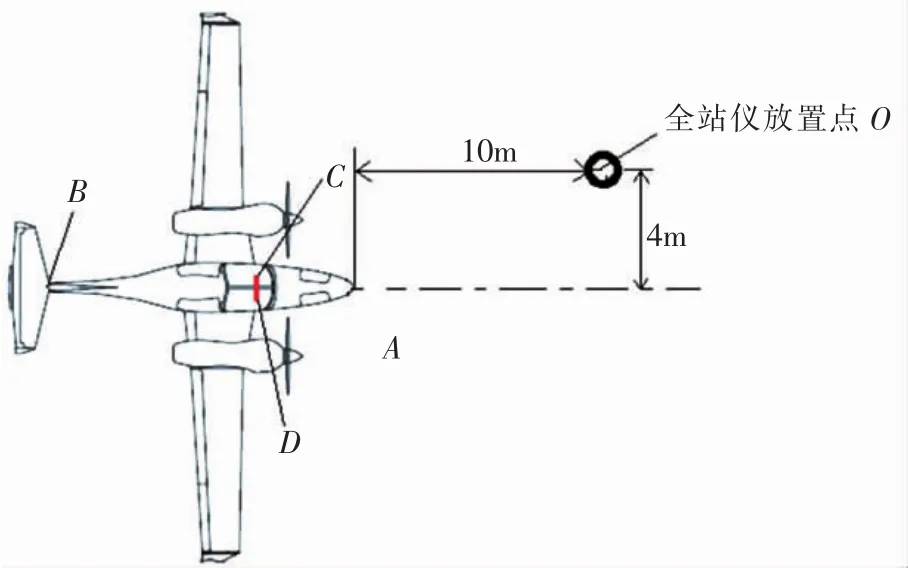
图2 全站仪与飞机放置的相对参考位置

为提高测量精度，分别在飞机对称面上的机头和平尾的位置各选择一测量点，如图2的A点和B点（该两点用于定位飞机的对称面）。在惯导安装过渡板上引出一垂直于设备航向基准面，在基准面上标识两个间距尽可能远的测量点C和D（该两点用于定位设备航向，定位距离的影响在下文的安装精度分析中有原因分析）。

2.2 利用全站仪测量基准点坐标方法

将全站仪测量光标对准机头测量点，设置全站仪测站点O点为坐标原点，后视角为0°，全站仪测量原理示意图如图3所示。全站仪的使用方法可参见所使用的设备说明书。在同一次测量过程中，应保持设备和飞机状态不可移动，否则会造成不同点的相对坐标出现偏差，一旦在测量过程中误碰到全站仪或飞机，导致其出现可能的微移动，应重新测量。

图3 全站仪测量原理示意图

在光标对准A点时，记录A点的坐标（N1，E1，Z1），同样方法分别记录 B （N2，E2，Z2），C（N3，E3，Z3），D（N4，E4，Z4）。四个坐标点测量完成后，即可开始数据分析。

在CATIA软件的曲面设计模块中，以全站仪测得的 N、E、Z值分别表示 X、Y、Z值，分别绘制 A、B、C、D四点，则xy平面即为水平面，如图4所示。由于测站点坐标为坐标原点，所以在CATIA中的原点即为观测点位置。通过O点沿X轴正向作一直线，用于视图中观察X轴的方向，如图中直线OA，此直线仅供视觉辅助，便于理解，不参与计算分析。

分别通过A、B点向水平面（xy面）作垂线，然后再利用此两条平行的垂线作一平面，由于A、B点为飞机对称面上的点，同时飞机对称面为与水平面垂直的面，故通过A、B两点的垂线所作的平面即为飞机对称面。利用CATIA中曲面相交的命令，得出飞机对称面与飞机水平面的交线，则该交线即为飞机的航向轴线。

本例中的C、D点利用水平仪进行了校准，为平行于水平面的点，同时该两点在设备的横轴和纵轴的平面上，因此该两点的连线即为平行于设备横轴的直线，通过测量直线CD与飞机对称面法线的夹角，即可计算出设备基准轴线与飞机基准轴线的偏差。（该处如果C、D点与水平面不平行，也可利用前述A、B点引垂线的同样方法作一平面来测量。此时，作出的平面的法线，即为设备的航向轴线，该轴线与前述A、B点作出的飞机航向轴线的夹角即为设备与飞机轴线的偏差。）

图4 CATIA中还原基准测量结果示意图

本例中，设备的水平面已在测量前调整至与飞机一致的水平面，因此，在后续的调整过程中，仅需要再调整设备的一个基准面与飞机的基准面重合即可。在实际操作中，为了保证安装精度，需要多次反复测量与调整，才能达到满意的安装精度。在操作时，为了判断调整方向，可将偏差夹角投影至飞机对称面和水平面，以辅助判断调整方向。

3 安装精度分析

设备在安装过程中，由于存在各种误差因素的影响，会降低设备的实际安装精度，如选取的基准点与真实基准的偏差、飞机和设备在调水平时的水平面误差、测量设备全站仪的测量精度导致的测量误差、附加的工装设备的制造误差等。由于机械制造加工的误差很小，相对于本例中其它误差情况基本可以忽略，故不再单独分析。

3.1 基准点位置误差分析

以2.2节的应用为例，分析基准点误差的影响。如图4所示，由于本例中A、B点无型架可提供支持，故A、B点的定位精度是由人眼识别的，误差较大。假如A、B点距离飞机实际对称面的误差为±1mm，A、B点在水平面上的投影距离为10m，则由A、B点在CATIA虚拟空间中作出的对称面与真实空间的对称面误差偏角为：

由本计算结果可知，由于A、B两点之间距离较远，一定程度上减小了两点本身误差对于基准面误差的影响。

本例中过渡板由于位于全站仪不可直接观测到的位置，故C、D点需要借用工装引出测量点，如图5所示。引出的测量工装采用刚度较好的刚性材料，以降低变形对测量精度的影响，同时为降低C、D点的轴线相对误差，将C、D点设置于工字型工装的前边缘上，在工装安装后，在其上表面用水平仪再次进行水平校准，通过该两种方式处理后，C、D点建立的轴线因工装引起的误差基本可以忽略（机械加工的平面度和直线度误差极小）。此时，只有水平仪校准时水平仪本身的测量误差，以精度为0.01°的水平仪为例，C、D点建立的轴线误差仅有0.01°。