图像自寻的火箭弹命中概率计算与分析

房施东，陈 栋，刘 桢，高 姗，周 到

(1.中国人民解放军陆军炮兵防空兵学院，安徽 合肥 230031；2.江西省军区数据信息室，江西 南昌 330006；3.陆军工程大学石家庄校区 十八大队，河北 石家庄 050000)

图像自寻的火箭弹是一款新型复合制导火箭弹,其通过采用北斗中制导+图像末端自寻的复合制导控制技术来提高命中精度。命中精度是衡量武器系统综合效能的重要指标。文献[1]通过分析制导炮弹弹道误差特性,考察影响射击精度的主要因素,建立了毁伤概率模型,通过蒙特卡洛法进行了仿真实验；文献[2]针对制导杀伤破甲子母弹特点，建立了射击误差模型，推导出毁伤概率计算公式，对其射击效率进行了评估；文献[3]探讨了导弹命中精度的评估过程，运用仿真技术与数理统计理论，通过建立精度评估仿真模型，实现导弹命中精度的评定。上述文献大多侧重于命中精度的影响因素、计算模型、仿真方法等的研究，但对于图像末制导火箭弹落点偏差与跟踪角误差、导引盲距之间的关系及其对命中精度的影响分析等方面的研究鲜有涉及，因此笔者拟在落点偏差分析的基础上构建落点偏差的数学模型，并探讨上述因素对命中概率影响规律，为该弹种研发与使用提供参考。

1 图像自寻的火箭弹落点偏差分析

1.1 落点偏差产生过程

图像自寻的火箭弹的导引头探测设备采用捷联方式，探测设备光轴与火箭弹主轴保持一致，因此在末段自寻的攻击过程中，火箭弹主轴偏离弹目视线的角度(即跟踪角误差)的大小决定了火箭弹偏离目标的程度。导引头采用追踪导引律[4]，使火箭弹始终保持对目标的闭环跟踪。然而随着火箭弹与目标距离的缩小，目标会充满探测器视场，从而使侦察导引头无法提取足够的目标特征，以致在相应的飞行时间内导引系统无法完成一个修正过程，则此时导引系统不能有效工作，此时的弹目距离称为导引盲距[5]。在导引盲距以内，火箭弹以惯性运动直至攻击目标。

因此火箭弹在进入导引盲距瞬时的跟踪角误差与导引盲距，以及在导引盲距内空气阻力、重力、风速、风向等因素，会使火箭弹落点与目标中心产生一定的距离，即落点偏差。

1.2 落点偏差数学描述模型

1.2.1 末段弹道模型简化及分析

由于导引头采用追踪导引律，火箭弹的速度矢量始终对准目标，因此在导引盲距范围内，若不考虑重力及空气阻力、风速风向等影响，火箭弹沿速度方向以直线轨迹攻击目标。然而，火箭弹在外界影响下，会以抛物线轨迹攻击目标。若将其简化为质点弹道，根据外弹道理论，建立非标准条件下的地面直角坐标系质点外弹道运动方程组(自由落体段)如下[6]：

(1)

式中：v为火箭弹运动速度；vx为纵向速度；vz为横向速度；vy为垂直速度;ρ为空气密度；d为弹径；m为弹箭质量；CD为阻力系数；g为重力加速度；Wx、Wz为橫风风速。

假设Wx=0 m/s，Wz=10 m/s，火箭弹在进入导引盲距瞬时坐标为 (0，300，0)，速度v0=500 m/s、俯仰角θ0=-80°、偏航角为0°.根据相关已知条件，根据上述弹道模型进行弹道解算，可得在纵向上由重力及空气阻力影响而产生的落点偏差量Δx约为0.589 m；在横向上由橫风影响而产生的落点偏差量Δz约为0.025 m。同理，可以计算不同初始高度y0条件下，落点偏差Δx、Δz如表1所示。

表1 不同初始高度条件下的落点偏差

可以看出随着高度y0的增加，|Δx|不断增大。当高度达到500 m时，|Δx|达到了2 m，而|Δz|虽然也增大，但是其值较小，|Δz|<0.1 m，因而可以忽略。

1.2.2 落点偏差数学简化模型

在导引盲距内，可运用直线弹道法分析落点偏差与跟踪导引角误差的关系。设导引盲距为L，在到达导引盲距瞬间火箭弹导引头位置为M点，火箭弹落点偏差与对目标的跟踪导引角误差关系如图1所示。

图1中，αz和αx分别为横向与纵向跟踪导引角误差。T(xt,yt,zt)点为目标点坐标，B(xb,yb,zb) 点为理论炸点坐标。Dx、Dz分别为纵向与横向的落点偏差量，其中Dx由重力及空气阻力影响而产生的落点偏差量Δx与纵向导引角误差引起的偏差量共同组成，则Dx-Δx即为纵向导引角误差引起的偏差量。设θm为弹目视线与垂直线夹角，则对单个落点存在如下关系：

(2)

由于αx、αz是火箭弹导引角系统偏差(设为βx、βz)和随机偏差(设为γx、γz)综合影响的结果，且数值较小，因此式(2)转换为[7]:

由于在弹道末段，图像末制导火箭弹以大俯仰角(约为-80°)运动攻击目标，因此θm值较小，对Dx影响微小；同时，βx、βz和γx、γz数值较小，为便于后续分析，将式(3)简化为：

(4)

在对Dx和Dz分别进行足够多次的采样处理后，可得出落点系统误差(μx，μz)近似值:

(5)

以及落点随机误差(σx，σz)近似值:

(6)

式中，θx和θz分别为纵向和横向跟踪导引角随机误差均方根值。

2 命中概率数学模型及分析

2.1 概率密度函数

以目标为原点建立坐标系xOz，其中x为纵向，z为横向，并假设落点偏差符合正态分布，则弹着点的联合概率密度函数可表示为[8]：

(7)

式中，ρ( 0≤|ρ|≤1)为横向、纵向落点偏差的相关系数[9]。

为了避免在x和z不相互独立(即0<|ρ|<1)时的复杂计算过程，假定ρ= 0，这往往可以通过合理设计控制律、控制好弹体姿态、避免弹体滚转来保证。此时，式(7)可简化为:

(8)

2.2 命中概率计算模型

导弹命中精度常采用圆概率误差CEP (Circular Error Probable，CEP)表示[8]。 图像自寻的火箭弹虽然在性能上具有导弹特点，而炮兵射击理论却习惯于对一定正面和纵深的矩形目标进行命中概率的计算分析[10]。为便于交流，采用此方法。设目标幅员的正面和纵深分别为2Lz和2Lx，根据式(8)所示概率密度函数，对于静止目标则有一发图像末制导火箭弹命中目标的概率为：

(9)

根据式(9)，给定σx，σz，μx，μz这4个参数，在落点偏差服从正态分布条件下即可求出对应的P，即命中概率值，同时，也可以依据给定P值，分解确定火箭弹末制导段系统误差(μx，μz)和随机误差(σx，σz)[7].

对于运动目标，设vt为速度，φ为速度与坐标z轴夹角，t为火箭弹在导引盲距L内的运动时间，则在时间t内目标在距离与方向上的运动距离为(vttsinφ，vttcosφ).根据误差原理，可以把此运动距离归为系统误差，则有图像末制导火箭弹对运动目标的命中概率为：

(10)

根据式(10)，已知t、φ、σx、σz、μx、μz的条件下，可以分析速度vt对命中概率的影响，亦可反推速度阈值，从而确定火箭弹对不同运动速度目标的适用性。

2.3 命中概率影响分析

在x和z轴向落点偏差符合正态分布且相互独立不相关假定下，根据式(5)、(6)、(9)、(10)，即可通过MATLAB 7.0数学软件计算和分析命中概率P与导引盲距、跟踪角系统误差、跟踪角随机误差及目标运动速度之间的关系。

图2为给定一组系统角误差和随机角误差典型值情况下(假定βx、βz、θx和θz分别均为1.0°，vt=0)，命中概率P随导引盲距L的变化情况(幅员分别为8 m×8 m与4 m×4 m)。对于8 m×8 m目标，当L≤100 m时，命中概率P不小于0.8，受L影响较小；当100 m250 m时，P减小到 0.2.对于4 m×4 m目标，其曲线变化类似，命中概率P受L影响更明显。很显然，要实现高的命中概率，应尽量缩短导引盲距。

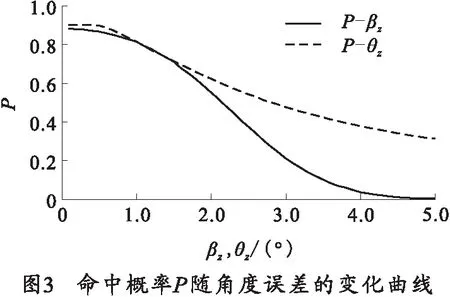
目标幅员为8 m×8 m，vt=0，假定其他角误差值均为1.0°，导引盲距L为100 m,命中概率P随βz与θz的变化曲线如图3所示。P随纵向角误差的变化曲线未给出，与此类似。总体来看，角误差较小时(2°以内)，βz与θz对P的影响差不多；但是随着角度误差的增大(大于2°)，βz对P的影响较θz更大。

对于运动目标而言，根据导引盲距L与火箭弹末段运动速度，可以确定火箭弹在导引盲距上的运动时间t.假定角误差值均为1.0°，目标幅员为8 m×8 m，目标运动速度与坐标z轴夹角γ=0°，则L分别为50 m与100 m时，命中概率P随目标运动速度vt的变化曲线如图4所示。

比较两条曲线可以看出，在不同导引盲距条件下，目标运动速度vt对命中概率P影响差别较大。L=50 m情况下，当-20 m/s≤vt≤40 m/s时，P≥0.85，受vt影响较小；超出此范围，随着运动速度绝对值的增大，P值迅速减小。考虑到μx、μz的影响及vt方向的不确定性，运动速度|vt|≤20 m/s，能够保证命中精度P≥0.85.在L=100 m情况下，P受vt影响更大，运动速度|vt|≤5 m/s，才能够保证命中精度P≥0.6.

通过对图2～4分析可知，如果已知火箭弹的导引盲距、跟踪导引系统角误差和随机角误差均方值及目标运动速度，则在落点偏差符合正态分布假设前提下，可根据前述数学关系式计算相应的命中概率P值，预测是否能够达到指标要求。反之，给定对目标(已知幅员与运动速度)的命中概率P值，可以分解确定对应给定导引盲距的跟踪导引角误差(系统误差及随机误差均方值) 的指标要求。利用软件计算分析知：

1)系统与随机角误差的指标上限在P指标的限制下随导引盲距增大而减小。

2)由于系统角误差和随机角误差综合影响落点偏差，因此满足P指标要求下，一个小些，另一个就可大些。

3 图像自寻的段命中概率仿真计算

3.1 导引盲距计算

导引盲距L与火箭弹控制特性、末段速度、侦察导引性能、目标及背景的特性等有关。因此可以根据上述条件估算导引盲距。

根据制导控制周期与末段速度(会受射程等因素影响,在此取680 m/s)可得导引盲距L1：

L1≈周期×末段速度=

(20/1 000)s×680 m/s=13.6 m.

根据探测视场角(10°)与目标幅员(8 m×8 m)可得导引盲距L2：

L2≈4 m×cot(10°/2×π/180) =45.7 m，

则L取L1与L2中较大值：L=L2=45.7 m.

因此，可以采用L≈50 m的数据对跟踪导引角误差指标进行设计。

3.2 导引角误差指标分析

对于8 m×8 m的静止目标，要求命中概率P值为0.5，在L=50 m,Δx=-0.04 m时，则利用MATLAB对角误差指标进行计算分析，结果如表2所示。

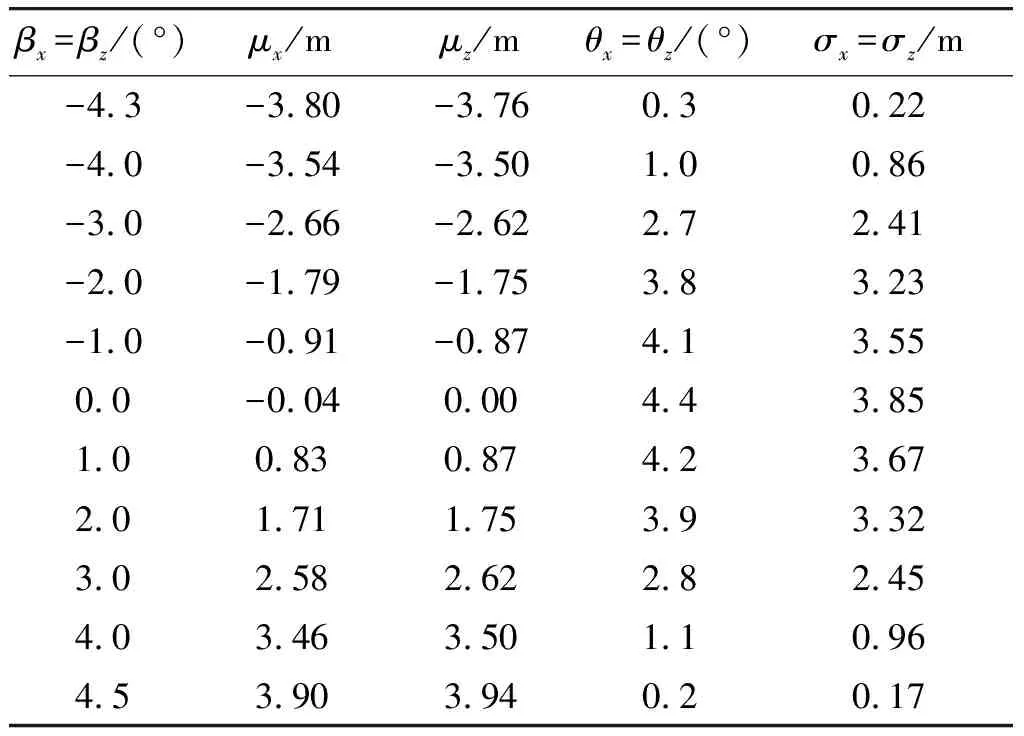
表2 跟踪导引角误差和落点偏差分解计算值

从表2中可见，对于50 m的导引盲距，跟踪导引角误差(系统误差+随机误差均方值)控制在4.5°以内即可。

3.3 命中概率仿真

从表2中选取4组典型数据，运用MATLAB软件基于蒙特卡罗法分别进行10 000次炸点散布仿真，其散布如图5所示。

图5中落入中间8 m×8 m正方形的模拟炸点数量N，即为命中的弹数。由命中概率P=N/10 000，得到4组命中概率P=[0.497 8，0.504 4，0.502 3，0.498 6].

4 结束语

在火箭弹落点偏差符合正态分布的假设条件下，结合图像自寻的火箭弹的工作过程，依据建立的落点偏差模型与命中概率模型，仿真分析了命中概率与导引盲距、跟踪导引角误差及目标运动速度之间的关系，提出了满足命中概率要求的跟踪导引角误差的技术指标，并验证了指标的科学性，为该弹种研发与使用提供了参考。另外，跟踪导引角误差影响因素的分析等问题还需要进一步研究。