抽筒子疲劳裂纹扩展研究及剩余寿命预测

朱永梅， 姚 祥，倪路瑶，唐文献，贾兰俊

(1.江苏科技大学 机械工程学院，江苏 镇江 212003；2.江苏科技大学 江苏省船海机械先进制造及工艺重点实验室，江苏 镇江 212003；3.中国船舶重工集团公司第713研究所，河南 郑州 450015)

现阶段的火炮在服役时，经过一定发数后零部件上开始出现较微小的裂纹。随着火炮的连续发射作业，该裂纹会逐渐生长。裂纹生长至临界断裂长度后，裂纹会开始快速扩展，该部件将会断裂。较多事例表明，这种疲劳裂纹引发的机械部件的断裂故障是十分常见的[1-2]。抽筒子是火炮射击后完成抽筒动作的关键部件，由于受到冲击载荷的作用，抽筒子会发生疲劳断裂，导致炮弹发射后药筒无法抽出，从而使火炮失去战斗力，在实际射击试验中也多次发生过抽筒子断裂的故障[3]。所以，为了提高火炮的安全性和可靠性，需要对抽筒子炮钢材料的裂纹扩展性能和疲劳剩余寿命进行研究。

近年来，我国对火炮疲劳寿命的研究不断深入，胡慧斌等[3]使用ADAMS建立了火炮的虚拟样机，模拟发射工况，输出抽筒子承受的载荷谱，结合材料的S-N曲线，建立了冲击载荷作用下火炮抽筒子的疲劳损伤与寿命模型。朱超等[4]建立了自行火炮炮闩系统虚拟样机模型，得到抽筒子爪在抽筒过程中的载荷谱,基于有限元技术建立了抽筒子有限元模型，对抽筒子进行了静强度分析，进而利用疲劳分析软件对抽筒子进行了疲劳寿命预测。易当祥[5]针对火炮行动系统的疲劳断裂，采用边界元法计算应力强度因子。Leonel等[6]采用了边界配置法进行应力强度因子的计算。目前对于抽筒子的疲劳断裂研究主要都是利用软件进行仿真分析，但是在抽筒子产生裂纹的条件下，很少有关于剩余寿命的评估及计算方法进行研究的文献。

笔者以某炮炮闩机构的抽筒子为研究对象，针对抽筒子材料45CrNiMoVA，开展室温下断裂韧度和疲劳裂纹扩展试验，测试材料的断裂韧度，结合实验数据拟合得到Paris断裂公式。根据抽筒子在抽壳工况下的受载情况，以Paris公式为理论依据，建立抽筒子剩余寿命计算模型，并讨论了应力、初始裂纹长度和材料断裂韧度3种因素对抽筒子的剩余寿命的影响，并得到它们的关系曲线。

1 疲劳裂纹扩展规律试验

1.1 断裂韧度实验结果及计算

试验设备采用美国MTS810-250 kN电液伺服热机疲劳试验机。按照0.8 mm/min的加载频率加载至试样断裂，记录完整的P-V曲线。试验所用材料为45CrNiMoVA，室温下的力学性能如表1所示。参照文献[7]，采用三点弯曲试样SE(B)，对其平面应变断裂韧度进行试验研究。

表1 45CrNiMoVA的力学性能

试验选用4块宽度为40 mm，厚度为20 mm的板材，分别标号为1#、2#、3#、4#，其中1#试样的断面放大图如图1所示，取厚度方向1/4、1/2和3/4三处从缺口到裂纹前缘的长度分别为a2、a3、a4，其平均值作为裂纹长度a。而且a2、a3、a4之间任意两个测量值之差不得大于0.1a，若不满足这些条件试验结果无效。试验所得的P-V曲线如图2所示,因为45CrNiMoVA材料是高强度钢，这种类型材料一旦产生裂纹后，裂纹尖端不能产生钝化，会迅速发生扩展直至断裂。根据文献[8]临界载荷FQ等于Pmax.

45CrNiMoVA材料的断裂韧度试样尺寸参数及试验测得的结果如表2所示。

表2 45CrNiMoVA的力学性能

1.2 疲劳裂纹扩展速率试验结果

根据抽筒子在抽壳工况下的应力分布情况，对试样加载14～1 400 MPa的循环应力，试样的应力加载方向与裂纹垂直，加载波形为正弦波，频率为10 Hz，加载应力比取0.1。参照文献[8]，采用标准拉伸C(T)试样，厚度为12.5 mm，有效宽度为50 mm，试样切口长度为12.5 mm，采用ΔK控制法得到预制裂纹长度为2.5 mm，试样如图3所示。

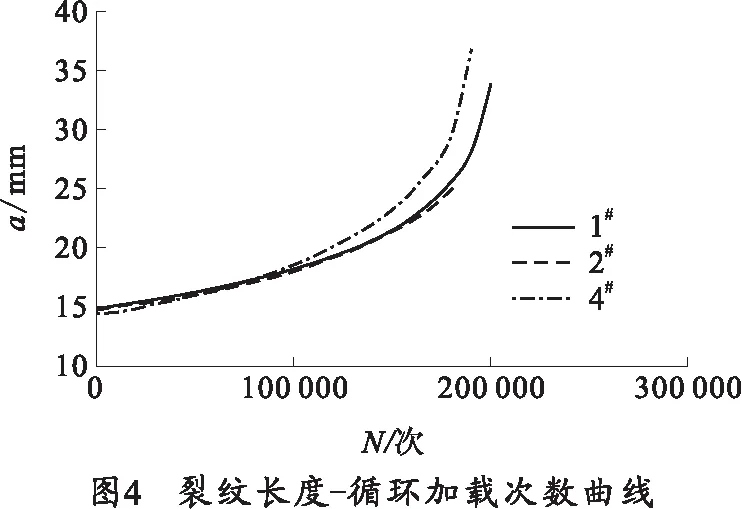
试验采用4个C(T)试样，分别记作1#、2#、3#、4#，并对试验结果取平均值。由于3#试样在试验开始时发生裂纹横向萌生，结果无效，其他试样的疲劳裂纹扩展量a与反复加载次数N的关系如图4所示。

由图4可知，在横幅循环载荷作用下，裂纹长度在14.85 mm左右开始发生扩展，随着加载次数的递增，裂纹扩展速率缓慢增加，在加载次数约135 000次以后，裂纹扩展速率快速增大，裂纹快速扩展，直至发生断裂，3个试样从裂纹发生扩展到断裂时加载次数为180 000～200 000次，最终裂纹长度为24.79～37.14 mm.

1.3 疲劳裂纹扩展速率计算

将1#、2#、4#试件的试验数据，拟合成裂纹扩展速率和应力强度因子的关系，如图5所示。其中，2#试样的无效点很多，3组试验数据在对数坐标系中均呈线性相关，且变化趋势一致。可以看出该炮钢的疲劳裂纹扩展速率随应力强度因子的增大而提升。

Paris疲劳裂纹扩展速率为

da/dN=C(ΔK)m,

(1)

式中：a为裂纹长度；N为应力循环次数；da/dN为裂纹扩展速率；ΔK为应力强度因子变化幅值；C和m均为材料常数，由实验数据测得：

(2)

式中：Kmax为抽筒子的应力强度因子最大值；Kmin为最小值，由于抽筒子承受的是冲击载荷，Kmin则为0；α为形状因子；Δσ为应力幅值。

根据曲线拟合得出C和m的值，如表4所示。由于45CrNiMoVA材料为高强度炮钢，硬度、强度较大，试验时受外部因素影响较大，容易出现表3所示m值波动大的现象。

表3 裂纹扩展试验结果

计算平均值，取C为2.578×10-11，m为2.859，查阅材料手册[9]得知，45CrNiMoVA材料的C=2.614×10-12，m=2.827，与试验的计算结果对比可知，m值相差不大，但C值相差较大，比查阅值大了约10倍。因为在疲劳裂纹扩展后期，裂纹长度及尖端的强度因子较大时，惯性致使尖端振幅高于试验所需要的幅值，使裂纹扩展速率变快，这可能是造成数据偏差的主要原因。通过阅读文献[10]，发现其他研究者在计算材料C和m值时也会存在一定的偏差，因此在后面的计算中采用本试验得到的C和m值。所以，45CrNiMoVA材料的Paris断裂公式为

da/dN=2.578×10-11(ΔK)2.859.

(3)

2 抽筒子剩余寿命估算

2.1 疲劳裂纹剩余寿命估算理论依据

根据断裂力学理论，将疲劳裂纹扩展分为3个区域：第I区为裂纹不扩展区，此时ΔK<ΔKth，其中ΔKth为疲劳裂纹扩展门槛值；第II区为裂纹临界扩展区，此阶段为估算疲劳裂纹剩余寿命的主要区域；第III区为裂纹快速扩展区，裂纹扩展速率极高，裂纹扩展寿命极短，可忽略。

疲劳裂纹扩展速率da/dN-ΔK曲线仅受材料自身、加载条件、试验环境等影响，不会因为试样的形状或尺寸产生变化。本文通过试验获取的Paris断裂公式(3)来预测出抽筒子疲劳裂纹扩展寿命。

当应力强度因子幅值ΔK比疲劳裂纹门槛值ΔKth大，裂纹将发生扩展，否则，裂纹不扩展；即：

ΔK>ΔKth,

(4)

现有的研究表明[11]，使用各种测试方法得到的初始裂纹尺寸为0.05～0.50 mm.因此本文在预测抽筒子剩余寿命时将抽筒子初始裂纹尺寸确定为a0=0.5 mm.

将式(1)积分，可得疲劳裂纹扩展寿命计算公式，即从初始裂纹扩展到临界裂纹的应力循环数为

(5)

临界裂纹尺寸ac的取值可由裂纹处的应力强度因子及材料的断裂韧性确定：

(6)

式中：KIC为材料的断裂韧度；σmax为循环应力的最大值。

对于无限大板，形状因子α和裂纹尺寸a无关，可得：

(7)

式中：C1=Cαmπm/2；Np为从初始裂纹尺寸a0扩展到临界裂纹尺寸ac的应力循环数。

2.2 抽筒子疲劳裂纹扩展寿命

建立抽壳系统柔体动力学分析模型。通过抽壳系统的动力学分析得到，抽筒子在抽壳过程中分别与摇臂和药筒发生碰撞，碰撞接触处应力较大，超过材料的屈服极限，但只出现在接触表面很小的一部分区域，且作用时间很短，准确性不高，对整体的结构不会产生很大的影响。所以笔者主要分析抽筒子中部的应力情况。

抽壳过程中抽筒子爪部与药筒接触部分所受最大载荷为38 kN[12].通过建立抽筒子等效有限元模型，得到其危险点应力云图如图6所示。

抽筒子的表面裂纹可视为单边裂纹，形状因子a为1.12，由式(6)可得临界裂纹长度：

(8)

由式(8)求得最终抽筒子疲劳裂纹扩展寿命为

(9)

2.3 抽筒子剩余寿命影响因素分析

2.3.1 不同应力场下抽筒子的剩余寿命

根据本文的试验条件，初始裂纹长度确定为0.5 mm ,由上文计算得临界裂纹长度为3.94 mm，通过剩余寿命预测模型可得应力与裂纹扩展寿命之间的S-N关系曲线，如图7所示。由图7可知所受应力越小的情况下，抽筒子的剩余寿命越大，且在应力为400～800 MPa区间内，剩余寿命增大缓慢，而在200～400 MPa区间内增大非常迅速，其中300 MPa时寿命为16 196次;200 MPa时寿命约为51 624次，增大了约3.2倍。

2.3.2 不同初始裂纹长度下抽筒子的剩余寿命

应力恒定为600 MPa时，改变已存在的裂纹长度得到该裂纹的剩余寿命，计算得出的关系曲线如图8所示。由图8可知应力恒定时，当初始裂纹长度从0.5 mm增大到1 mm时，剩余寿命减小幅度最大，减小了约1.8倍(约1 000次)。

2.3.3 不同断裂韧度下抽筒子的剩余寿命

改变材料的断裂韧度，计算可得到不同的临界裂纹长度，通过剩余寿命预测模型得到相应的剩余寿命，如图9所示。由图9可知，材料的断裂韧度越大，剩余寿命越大，且增长的趋势越来越缓慢，可见当材料断裂韧度越大，对剩余寿命增大的影响越来越小。

3 结论

1) 根据疲劳裂纹扩展速率实验数据拟合出裂纹扩展速率和应力强度因子的关系曲线，进而拟合得出C和m的值，得到了45CrNiMoVA的疲劳裂纹扩展公式。

2) 设定初始裂纹长度为0.5 mm，通过材料的断裂韧度计算可得临界裂纹长度为3.94 mm，根据剩余寿命预测模型，估测抽筒子的剩余寿命为2 232次。

3) 通过对抽筒子剩余寿命的影响因素分析可知：当应力由300 MPa减小至200 MPa时，剩余寿命增大幅度最大，约3.2倍；应力恒定时,当初始裂纹长度从0.5 mm增大到1 mm时，剩余寿命减小幅度最大，减小约1.8倍；在合理范围内，材料的断裂韧度越大，剩余寿命越大，且剩余寿命增长的趋势越来越缓慢。