电磁轨道炮U形铝质电枢回收过载极限分析

王俊晓，向红军，吕庆敖，张华祥

(陆军工程大学石家庄校区 弹药工程系，河北 石家庄 050003)

电磁轨道炮是一种靠电磁力发射超高速弹丸的动能武器，具有速度可控、噪声污染小、安全系数高等作战优势，长期以来一直受到各军事强国的高度重视，电磁发射技术也一直是当前各军事强国研究的重点[1-3]。目前我国电磁轨道炮技术的发展仍存在诸多瓶颈，如材料寿命短、电源密度低、系统效率低等问题[4]，当电枢在膛内加速运动时，电枢会受到复杂的作用，从而导致枢/轨间的滑动电接触状态极易处于不稳定的状态，并产生烧蚀、刨削等损伤现象，严重影响轨道的寿命从而制约电磁轨道炮的进一步发展，而对轨道和电枢之间的滑动电接触进行实时监测是很困难的，目前的研究方法是根据基本理论建立超高速滑动电接触模型，预测滑动电接触的过程和对轨道及电枢界面的影响，并对发射后的滑动接触界面形貌与理论预测进行比较，反推滑动电接触过程。因此，要实现枢轨之间滑动电接触的可靠分析，需要将发射后的电枢进行无损回收，而保证无损回收的关键点在于电枢在回收过程中受到的最大过载不超过其所能承受的极限值，因此研究电枢可承受的极限过载值在电枢无损回收中有着重要的意义。

电磁轨道炮经过几个阶段的发展，目前在电枢选择上多为U形电枢[5-8]，而金属铝由于其良好的导电性能、较低的密度等因素成为电枢材料的首要选择，吕庆敖等[9]曾详细阐述了U形铝质电枢的六大优势，因此笔者对U形铝质电枢可承受的极限过载进行研究,利用非线性动力学有限元软件LS-DYNA，研究了将U形铝质电枢分别以不同的速度侵入不同密度的回收介质时的变形情况及所受过载大小，通过电枢变形的临界情况，分析了无损回收条件下U形铝质电枢在可承受的最大过载值及不同初速的电枢回收可选介质的最大密度，为电磁轨道炮电枢的无损回收技术实施打下了基础。

1 有限元仿真模型

1.1 仿真模型的建立

完整的数值模型由电枢、空气域、回收介质域3个部分组成，电枢采用常应力实体单元算法，空气域和回收介质域采用中心单点积分的ALE多物质单元算法。

在实体建模过程中电枢和流体域部分可相互独立，而空气域和回收介质域接触部分必须紧密连接以保证在网格划分的时候二者可以共节点，保证物质可以在两个区域的网格内流动。根据文献[10]中的观点，为了保证结构入水产生的冲击波可以在流场中顺利传播，一般选取水域的宽度应为结构宽度的4～5倍。建模时电枢宽度为20 mm，空气域和回收介质域宽度为100 mm，整个模型厚度为2 mm.对空气域和回收介质域四周施加无反射独立边界，上下两面(包括电枢)施加对称边界。网格划分时厚度方向划分一层，流体域网格尺寸设置为2 mm，为了保证电枢头部曲线部分网格的均匀性和致密性，设置曲线部分网格20份。其仿真模型如图1所示。

1.2 材料模型

对上述模型添加材料属性，其中电枢定义为非线性铝合金材料，用关键字*MAT_PLASTIC_KINEMATIC定义，各项参数的设置如表1所示。

表1 电枢材料参数设置

空气采用*MAT_NULL材料模型及*EOS_LINEAR_POLYNOMIAL状态方程加以描述[11]。线性多项式方程表示单位初始体积内的线性关系、压力值，即:

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E.

(1)

回收介质采用*MAT_NULL材料模型及*EOS_GRUNEISEN状态方程表示，冲击波速度vs-粒子速度vp的三次曲线Gruneisen状态方程定义压缩材料的压力为

(2)

式中：C为冲击波速度vs，即vs-vp曲线的截距(速度单位)，由于在数值上与声音在介质中的传播速度相同，有时也称其为声音在该介质中的传播速度；S1、S2、S3分别为vs-vp曲线斜率的系数；γ0是Gruneisen常数；a是常数，对γ0的一阶体积修正。

回收介质各参数具体设置如表2所示。

表2 回收介质Gruneisen状态方程参数设置

1.3 流固耦合设置

模型涉及固体电枢及流体域，故需进行流固耦合设置，流固耦合主要靠关键字*CONSTRAINED_LAGRANGE_IN_SOLID来实现，定义耦合类型为加速度和速度约束型，即完成流固耦合关键字的设置，实现了电枢与流体耦合时力的传递。在*CONTROL_ALE中设置默认的介质数值方法为ALE方法，两次对流间的循环数为1，对流方法为二阶精度的Van Leer + Half Index Shift.

2 仿真模型合理性对比验证

为了验证上述仿真模型的合理性，根据文献[12]开展的平头弹丸入水实验，建立如图2所示的实体模型，其中平头弹丸长度为26 mm，弹径为12 mm，设置弹丸初速度与实验相同，分别为75.4、118.8、142.7 m/s，仿真得到的弹丸速度与位移随时间变化曲线如图3所示。

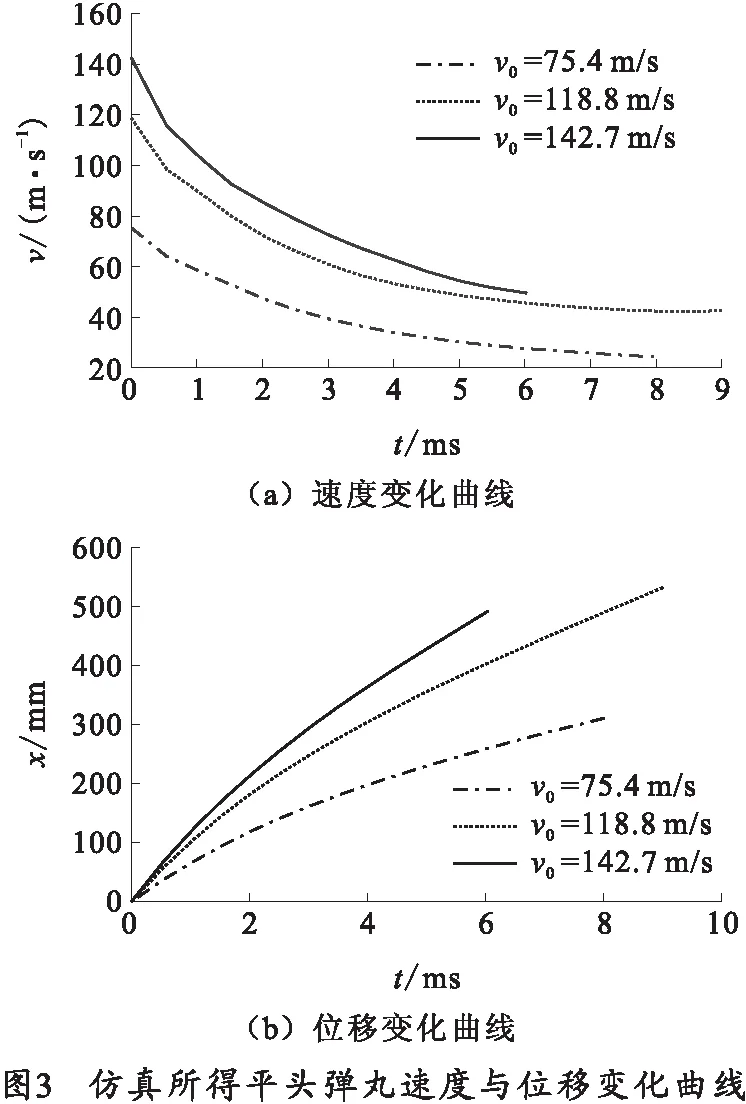
通过对比图3所示仿真结果与文献[12]中的实验结果，可以发现仿真得到的曲线与实验结果的速度及位移变化规律较为吻合，可认为本文中仿真模型在规律探索上存在合理性。

3 仿真结果及分析

电枢无损回收的根本要求是回收过程中受到的过载(反向加速度)值不超过其所能承受的极限，而是否超过其极限最直观的体现在于电枢回收后是否发生形变。因此，通过电枢回收过程中发生形变的临界值，确定电枢在回收过程中所能承受的最大过载，以及该速度下可选用回收介质的最大密度值。

3.1 不同初速电枢无损回收可选最大密度介质分析

设置电枢初始速度为2 500 m/s，修改K文件改变回收介质的密度，并观察电枢的变形情况。图4为介质密度分别为20、30、35 kg/m3时电枢的变形情况。

通过观察图4可以发现，电枢进入密度为20 kg/m3的介质时不发生形变而进入密度35 kg/m3的介质时发生了微小的变形，当介质密度为30 kg/m3时电枢恰好不发生变形，暂时认定初速为2 500 m/s的铝质U形电枢无损回收的介质最大密度为30 kg/m3.

同理，分别设置电枢初速为2 000、1500、1 000、700、400 m/s，修改K文件改变回收介质密度，并观察电枢的变形情况。通过分析对比得到如下结论：当电枢速度分别为2 000、1 500、1 000、700、400 m/s时，无损回收电枢可选用的介质最大密度为45、80、150、300、1 000 kg/m3。将上述6组结果绘成曲线，可得电枢速度与介质最大密度关系如图5所示。

从图5中可以看出，随着电枢速度的提高，可选用的介质密度减小，且减小幅度越来越小。在该范围内对曲线进行拟合，得到回收介质最大密度ρmax与电枢速度v的关系为ρmax=7×107×v-1.884，在该拟合曲线中R2=0.997 3，R2为度量拟合曲线拟合程度的可决系数，R2越接近1说明拟合程度越好。在图5中，曲线下方的阴影区域为安全区域，即电枢以该区域内的速度进入该区域内密度的回收介质均不会发生变形，该区域密度的介质是回收中可采用的回收介质。

3.2 电枢可承受最大过载分析

在上述分析中确定了不同初速的电枢无损回收可选介质的最大密度值，为了研究U形铝质电枢在回收过程中可承受的过载极限，将不同速度的电枢在对应的最大密度介质中的加速度绘成曲线，如图6所示。

从图6中可以看出，同样的模型下电枢速度越快,进入介质时的时间越短，不同速度的电枢进入其相对应的最大密度介质瞬间的最大过载值基本相同，数值上均为800 000g左右，稍有偏差是由于一定初速下回收介质的最大密度值是根据电枢的变形情况确定，而电枢未变形时的介质密度值与微变形时的介质密度值之间的情况尚未进一步研究，难免存在一定的误差。故而在本文研究误差允许的范围内，电磁轨道炮U形铝质电枢在回收过程中可承受的最大过载值约为800 000g.

4 结论

通过分析仿真结果可以得到如下结论：

1)不同初速度的电枢在无损回收过程中可以选用的介质最大密度不同，速度越快可选的介质密度越小。当电枢速度为2 500、2 000、1 500、1 000、700、400 m/s时，无损回收电枢可选用的介质最大密度为30、45、80、150、300、1 000 kg/m3．将其绘成曲线并进行拟合可得到一定范围内回收介质最大密度ρmax与电枢速度v的关系为ρmax=7×107×v-1.884，其中R2=0.997 3.

2)对于U形铝质电枢，在形状、材料一定的情况下，无论初速度值为多少，当电枢侵入该速度下回收可选的最大密度介质时，电枢所受到的过载均为800 000g左右，由此可得：在本文研究误差允许范围内，电磁轨道炮U形铝质电枢回收过程中可承受的过载极限值约为800 000g，只要电枢在回收过程中所受到的过载值不超过该极限均可实现无损回收。需要注意的是，本文的仿真

研究没有考虑回收过程中热的影响，虽然采用了流体介质会吸收一部分生成的热，但当电枢处于高速状态时，尤其达到1 500 m/s以上时，热的影响仍然比较明显，也会使材料的属性发生变化，比如质地变软等，因此实际过程中U形铝质电枢的过载极限值小于800 000g，热的作用对极限值的影响也是下一步需要研究的重点，同时材料的非线性问题也是需要考虑的因素。