改进降噪自编码的航空发动机气路故障诊断*

洪骥宇， 王华伟， 车畅畅， 倪晓梅

(南京航空航天大学民航学院 南京,210016)

引 言

发动机是飞机的心脏，实时而准确地进行发动机的状态监测与故障诊断，即可以提高维修效率、降低维修成本，也有利于做出正确的飞行决策，提高飞行安全。但由于发动机本身复杂的结构和恶劣的工作环境，存在着大量非线性和带有噪声监测特征，加上其故障模式多样及存在着关联故障、竞争失效等诸多情况，准确地进行故障诊断较为困难。

目前，进行航空发动机故障诊断一般分为3种方法：基于模型、基于知识及数据驱动的故障诊断方法。基于模型的故障诊断方法方面，如张鹏等[1]使用球面采样平方根无损卡尔曼滤波器进行发动机的故障诊断，在传感器故障的情况下仍取得良好效果。Lu等[2]使用扩展卡尔曼滤波器进行了发动机的状态估计。基于知识的故障诊方法，如陈果等[3]将铁谱、光谱及试车台数据知识规则整合为专家系统进行了发动机磨损故障诊断。赵薇等[4]使用故障树结合对球磨机振动信号的分析，对其机械部件进行了故障诊断。

随着航空发动机的结构越来越复杂，准确的性能模型、知识规则越来越难建立与确定，而基于数据驱动的智能诊断技术能满足时变非线性的诊断要求，使用越来越广泛。如崔建国等[5]使用动态主元分析提取特征并使用改进的SVM进行发动机的滑油系统的故障诊断。Lu等[6]使用RBF网络进行发动机气动故障诊断，最后结合D-S证据理论与SVM建立了气路融合诊断架构。Benyounes等[7]运用自适应模糊神经网络建立了工作系统的数学模型，通过该模型进行故障诊断。Nozari等[8]使用多层感知器(multi-layer perception,简称MLP)神经网络对燃气涡轮机建立了故障诊断与隔离方法。Zhao等[9]使用粗糙集预先处理数据并建立粗糙诊断模型，最后根据得到的结果使用BP神经网络进行故障诊断。曹冲锋等[10]将泛化搜索引入SVM的超参数选择中，利用改进的模型进行了故障诊断。

目前，基于数据驱动的故障诊断大多使用BP，RBF，SVM等机器学习算法来实现。这些算法使用标签数据进行训练学习，提取出故障特征从而进行分类，实现故障诊断。机器学习算法为以航空发动机为代表的复杂大系统进行故障诊断提供了可能，但也有其局限性和缺点：a.从传感器上直接得到的数据非线性极强，加上恶劣环境带来的噪声污染，使用这些浅层网络进行诊断会被噪声影响且难以挖掘数据之间的深层关系；b.浅层网络本身也有自己的局限，SVM对噪声较为敏感容易产生过拟合；c.BP等传统神经网络在训练过程中容易产生局部最优。

深度神经网络是最近机器学习研究的热点，由于其非线性表达能力极强，能够挖掘数据之间深层关系得到内在特征，已在图像识别、自然语言处理方面等领域取得突破进展[11-12],在故障诊断方面也有了一些进展。雷亚国等[13]使用深度信念网络对多级齿轮传动系统进行了健康状态识别。Li等[14]在对齿轮箱研究时，使用深度信念网络进行了故障诊断。笔者拟结合深度学习网络在其他领域应用的成果，结合航空发动机气路故障诊断的特点，采用降噪自编码器DAE通过贪婪逐层训练算法逐层提取特征，最终得到一个能够表征数据深层特征且更适合故障诊断的特征向量，然后将特征导入经过改进萤火虫算法进行优化的RBF网络进行故障诊断。本模型的优点在于通过深度结构、降噪训练，经过非监督学习得到了更能表征故障类型且更为鲁棒的深层特征，更利于分类；同时在原有DAE的基础上进行改良，分类器采用FRBF，分类性能进一步提高，能够更为准确地进行故障诊断。

1 航空发动机气路故障诊断问题

常见的气路故障有以下几种：积垢、腐蚀与侵蚀、热变形、物体打伤以及密封件疲劳等。但无论哪种故障都必然会导致某部件的性能下降，如压气机叶片的磨损会导致压气机效率的下降。部件性能的下降，也会使得测量参数跟着变化而偏离设计值，如图1所示[15]。为了检测故障，基于模型的方法一般是利用搭建好的模型的输出量与系统输出做偏差比较，以此来判断是否存在故障并定位故障原因。

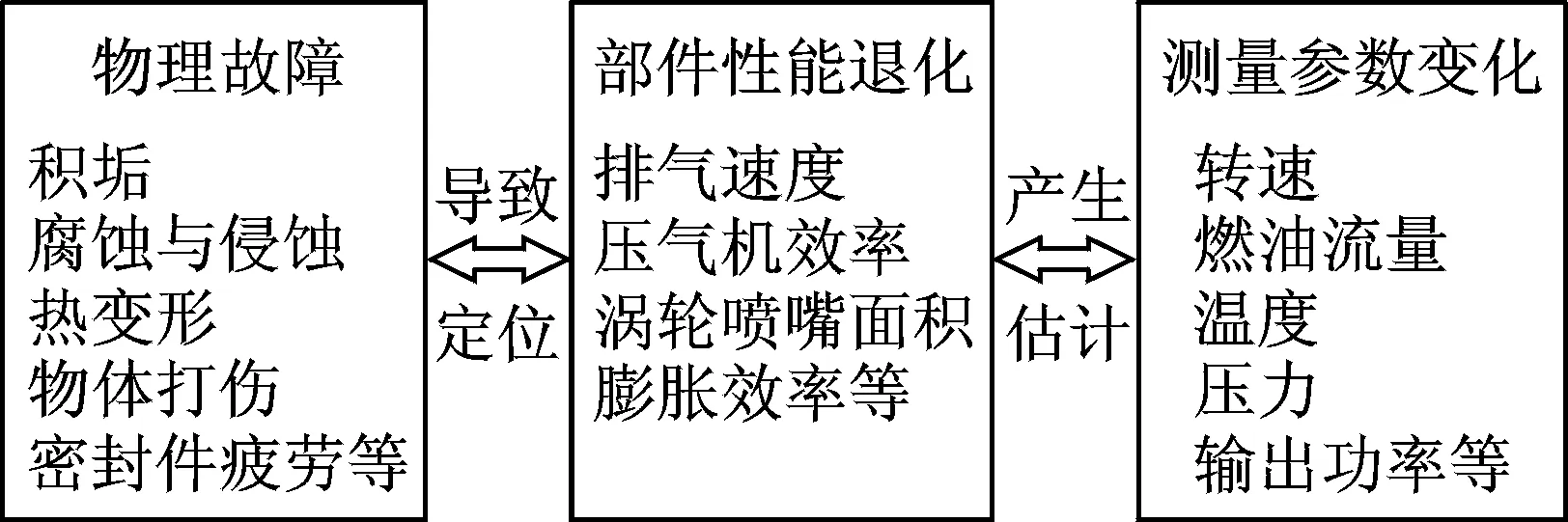
图1 航空发动机气路诊断分析Fig.1 Analysis of gas path diagnosis for aero-engine

如图1所示，反映部件性能退化的效率等参数被称为性能参数，这些参数一般难以直接测量；而转速、稳定、压力及燃油流量等可以直接测量的参数，被称为测量参数。笔者通过测量参数以及学习参数和故障之间的关系进行故障诊断。测量参数越多，越能够反映发动机当前工况，从而提高诊断率。但是由于传感器技术等原因，能测量的参数有限，并且在选取测量参数时需要遵守以下几个原则[16]:a.能够显著反映发动机状态；b.对故障敏感；c.测量参数之间相关性小。

考虑到发动机的健康管理与实际工作中的状态监测，选择以下4个参数进行故障诊断：排气温度EGT、燃油流量FF、高压转子转速N2和压转子转速N1。

2 航空发动机气路故障诊断方法设计

随着发动机越来越复杂，加上传感器技术与人工智能技术的发展，无需依赖模型精度的后者越发得到重视。但是，后者虽然得到了广泛的使用，仍然存在一些问题:a.相似故障由于测量参数类似，很难加以区分；b.测量参数中存着的噪音，对诊断精度有一定干扰；c.发动机具有很强的非线性，传统算法很难挖掘数据间的关系；d.传统算法自身存在一定局限，如SVM易受噪声干扰，BP易产生局部极值。针对上述问题，笔者使用改进的DAE算法进行航空发动机气路故障诊断。

2.1 气路故障诊断算法框架及流程

笔者使用的改进DAE算法分为两个部分，DAE部分和FRBF部分,如图2所示。

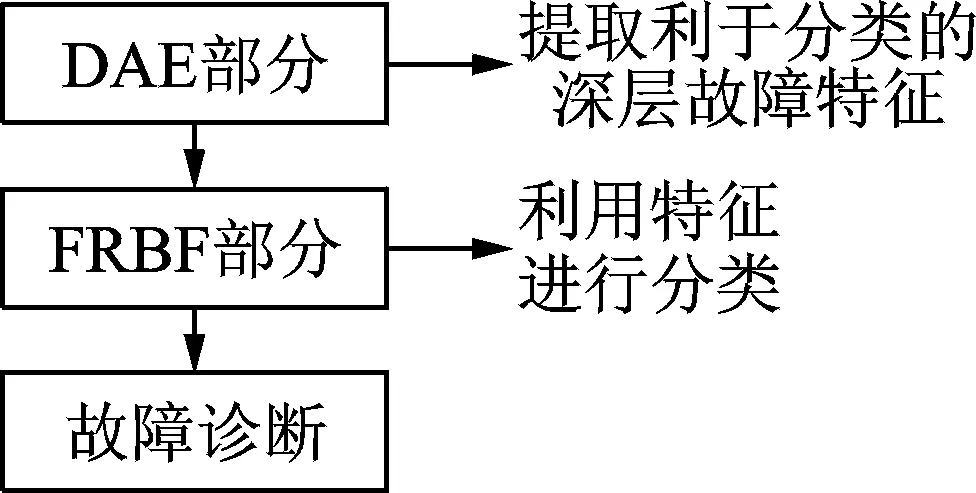
图2 算法框架Fig.2 Algorithm framework

DAE部分利用深层结构以及贪婪逐层训练算法，并通过在输入层加入“损伤噪声”训练出利于分类且更为鲁棒的深层故障特征。FRBF则是通过引入惯性权重与自适应光强因子的FA算法优化传统的RBF网络，得到分类性能更为优异的FRBF。最终，利用DAE部分得到的特征，使用FRBF进行故障诊断。

2.2 DAE

Hinton等[17]通过对受限玻尔兹曼机(restricted boltzmann machines，简称RBM)进行堆叠并使用贪婪逐层方法训练参数，取得了良好的效果。随后根据这一思想，Bengio等[18]提出了堆叠自编码(stack autoencoder，简称SA)。为了解决机器学习中的过拟合问题，降噪自编码器应运而生[19]。

2.2.1 自编码器

自编码网络分为3层：输入层、隐含层和输出层，而其核心部分又可分为编码和解码两部分。网络通过编码部分将数据进行重构提取特征，又通过解码部分将提取的特征进行还原与原输入进行对比，通过迭代，最终得到能够代表原始数据的特征参数。

编码部分中映射函数为

y=fθ(x)=s(Wx+b)

(1)

其中：s(x)为编码器的激活函数；θ为编码参数，由具体的函数模型参数W和b组成；y为编码后提取的特征。

解码部分的映射函数可表示为

z=gθ′(y)=s(W′y+b′)

(2)

其中：gθ′(y)为解码器的激活函数；θ′为解码参数，θ′由W′和b′组成。

要想使得提取的特征尽可能地代表原始数据，则损失函数需取最小值。损失函数L(x,z)定义如下

(3)

(4)

2.2.2 贪婪逐层训练算法

人脑在识别事物的过程中不止用了一层神经元，通过层层提炼事物的特征，才能准确地对事物进行判别。神经网络也是这样，每加入一层隐藏层，网络的表达能力都得到了进一步的加强。为了得到事物的深层特征，必须使用深度结构的网络来进行训练。由于训练算法的原因，在训练深度网络时不得不面对局部极值和梯度弥散等问题，这曾让深度网络停滞不前。而贪婪逐层训练算法，让这一问题得到了解决。

如图3所示，以3层隐含层为例。h为第1隐含层，按照正常的训练算法得到第1个隐含层的w和b之后，在进行第2隐含层训练时，以第1隐含层的输出作为第2隐含层的输入，而在进行第3隐含层训练时，则使用第2隐含层的输出作为输入。若隐含层数增加，也以此类推，最终得到能够表达数据信息的深层特征值。

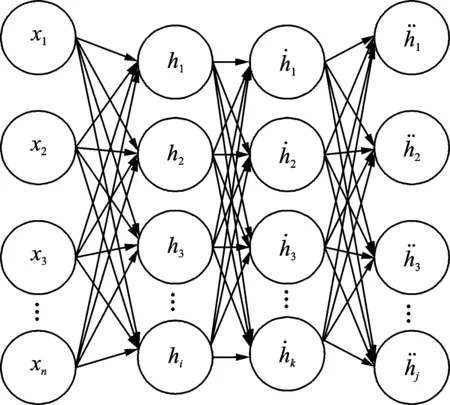
图3 贪婪训练的隐含层Fig.3 Hidden layer for greedy training

2.2.3 加躁训练环节

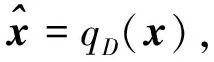
(5)

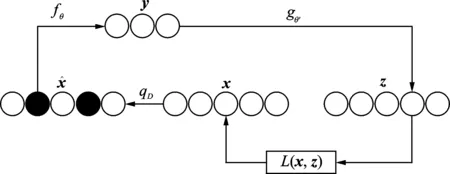
图4 降噪自编码器Fig.4 Denoising autoencoder

2.3 FRBF网络

2.3.1 RBF神经网络

RBF神经网络是一个3层前馈神经网络，如图5所示。

图5 RBF网络Fig.5 RBF network

其3层的节点数分别为n，h，m。输入向量为X=[x1,x2,x3,…,xn]T，输出向量为Y=[y1,y2,y3,…,ym]T。

当径向基函数选用高斯函数时，则隐含层的输出为

(6)

其中：i=(1,2，…，h)；ci为高斯函数的中心；σi为高斯函数的方差。

在得到隐含层输出之后，经进过权值分配，即可得到输出层

(7)

其中：i=(1,2,…，h)；j=(1,2,…，m)；ωij为连接隐含层和输出层的权值。

2.3.2 萤火虫优化算法

萤火虫算法[20]的基本思想是将每种解决方案当成萤火虫，而每一种方案的优劣程度决定萤火虫的亮度，而越亮的萤火虫会吸引周围的萤火虫向它靠拢。随着不停迭代，大部分的萤火虫会聚集到最亮萤火虫的周围，从而得到最优解。

萤火虫的亮度为

I=I0e-γrij

(8)

其中：I0为萤火虫自身的亮度，它取决于需要寻优的适应度；rij为任意点到萤火虫间的距离；γ为光强吸收因子，用来决定萤火虫的光亮范围。

定义吸引度为

(9)

其中：β0为距离为0时萤火虫的吸引力；m为指定的指数参数，本研究定义为2。

若两个萤火虫i和j，其中一只亮度大于另一只，如I0(j)>I0(i)，则i受到j的吸引而进行位置更新

xi(t+1)=[xi(t)+β(xj(t)-xi(t))+

(10)

其中：xi(t)，xi(t+1)和xj(t)分别表示萤火虫i的当前位置、下一时刻位置以及萤火虫j的当前位置；rij为萤火虫i与萤火虫j之间的距离；α为步长因子；rand为[0,1]上服从均匀分布的随机数。

2.3.3 改进的萤火虫算法

由式(10)可以看出，位置更新公式由3部分构成，虽然第3部分引入了随机部分，增加了寻优能力，但由于前2部分的系数固定，不能够随着迭代的进行而自适应变化，仍然存在着算法迭代初期寻优能力过弱容易陷入局部最优，迭代末期陷入在最优解附近震荡的僵局。为此笔者在文献[21]和[22]的基础上，将惯性权重与自适应变化的光强吸收因子引入萤火虫算法，具体改变如下

其中：τmax，τmin为最大权重、最小权重；t,tmax为当前迭代次数和最大迭代次数；γ0为初始的光强吸引因子；diter为一个在(0,1)范围内的衰减系数。

通过调整惯性权重τ(t)，在迭代初期得到较大的τ(t)，此时算法的移动步长较大，全局搜索能力较强，不易陷入局部最优；而到了迭代后期得到较小的τ(t)，这时算法的移动步长较小，逐步逼近最优值，而不会在最优值附近陷入距离震荡。光强吸引因子γ可以看做是萤火虫的吸引范围，当其很小时的萤火虫对很远的萤火虫也有着较强的吸引力，而当其很大时只能吸引一定范围内的萤火虫。在迭代初期使其较大，萤火虫会聚向周围较亮的萤火虫而不会只向一个萤火虫移动，这样便能减小陷入局部极值的可能；而在迭代末期使其变大，这样便可以从所有的范围中甄选出最优解。

2.3.4 基于萤火虫优化算法的FRBF

RBF网络的性能主要取决于ci，σi，ωij、函数的中心、方差与权值，在使用原始RBF网络进行分类时，往往不能得到最优的参数，为此使用改进之后的萤火虫算法对RBF进行优化，从而提高其性能。具体步骤如下：

1) 对数据进行预处理和归一化；

2) 初始化萤火虫算法参数，如步长因子α、光强吸引因子γ和最大吸引度β0等；

3) 初始化萤火虫种群的位置，以ci，σi和ωij进行编码；

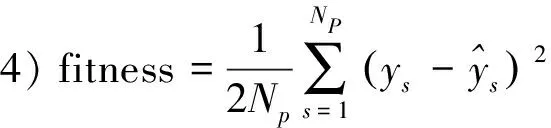
5) 计算萤火虫种群个体中的各个亮度，确定吸引度与移动步长；

6) 得到新的萤火虫个体亮度，并确认是否达到结束条件，达到则进行下一步，否则回到上一步；

7) 对最优个体进行解码，得所需的RBF参数；

8) 利用训练好的RBF网络进行预测。

3 基于降噪自编码和FRBF的航空发动机气路故障算法

如图6所示，基于降噪自编码和FRBF的航空发动机气路故障诊断流程如下。

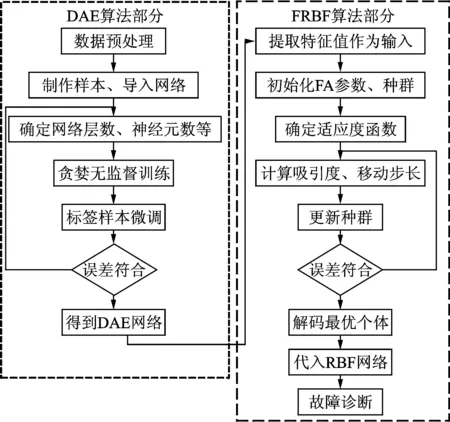
图6 诊断流程Fig.6 Diagnostic process

DAE部分：

1) 数据预处理并对数据进行归一化处理；

2) 制作样本，分为训练样本与测试样本，并将其导入网络；

3) 确定网络各参数，如网络层数、隐含层神经元数等；

4) 使用贪婪逐层训练算法进行无监督训练，在每一层进行训练时，使用下式获取各隐含层最优参数θ和θ′

5) 使用标签样本进行有监督的微调；

6) 满足误差条件则进行下一步，否则回到第3步；

7) 得到训练好的DAE网络。

RBF部分：

1) 使用DAE网络中提取的特征值作为RBF网络输入；

2) 初始化FA算法参数如步长因子α、光强吸引因子γ和最大吸引度β0等，并初始化其种群；

4) 计算萤火虫种群个体中的各个亮度，确定吸引度与移动步长；

5) 更新种群，并确认是否达到结束条件，达到则进行下一步，否则回到上一步；

6) 对最优个体进行解码，得所需的RBF参数；

7) 将参数带入RBF网络；

8) 进行航空发动机气路故障诊断。

4 实例分析

为了验证笔者提出方法的有效性，利用从某型发动机采集到的故障样本来检验算法的有效性。监测了所选取的4个参数EGT，FF，N2和N1进行故障诊断，并进行偏差化与归一化处理，EGT采用绝对偏差，其余采用相对偏差，归一化公式如下

(14)

使用参数进行的故障诊断类别如表1所示，每种故障有30个样本，一共300个样本。其中200个作为训练样本，另外100个作为测试样本。

表1 故障类别

为了校验提出算法DAE-FRBF的效果，笔者选择原始DAE、萤火虫算法优化的FRBF网络、RBF及SVM进行比较，所有的程序都在Matlab中运行。其中原始DAE与提出算法的DAE部分是一致的，隐含层都为4层，神经元数分别为6-8-8-10，其中去噪参数设置为0.2，dropout为0.3，dropout是深度学习中有效减少过拟合的一种方法。单独的FRBF与提出算法中的FRBF部分选择的参数一样，随机因子α取1.5，光强吸引因子γ取1，最大吸引度β0取1，RBF的隐藏神经元数取13。没有优化的RBF和SVM则分别使用Matlab自带工具箱与台湾大学林智仁开发的Libsvm工具箱进行运算。

为了减小样本选择对结果的影响，也为了避免算法的波动，选取10次样本进行试验，每次选取200个训练样本时(即每个故障抽取20个样本)，每种故障30个样本中随机选取20个作为训练样本，其余10个作为测试样本。测试结果如表2所示。

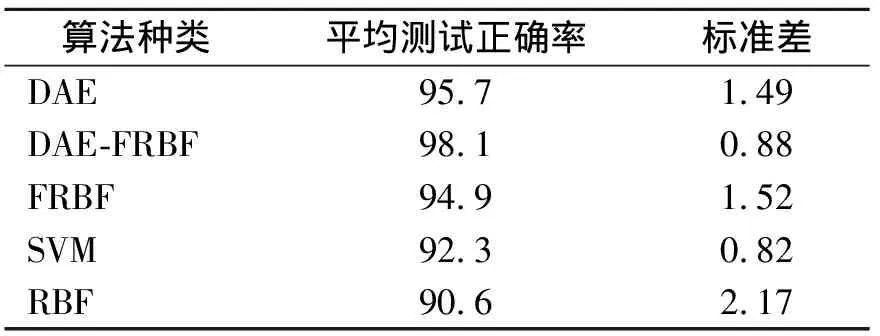
表2 各算法测试结果

由表2可知：没有经过优化的RBF正确率最低，且测试结果的波动幅度也较大；而SVM虽然正确率不是很高，但其稳定性却在5种方法中最佳；经过改进FA优化后的RBF效果有了明显的改善，不仅正确率得到了大幅度提高，稳定性也有了提升，体现了良好的分类性能；正确率最高的是使用深度网络提取特征的DAE与DAE-FRBF，其中又以后者为佳，诊断准确度和稳定性都有了提升，测试正确率达到了98.1%，标准差降低为0.88%。DAE-FRBF在DAE原有的基础上进行了改良，进行分类诊断时没有使用常用的SOFTMAX,而是利用FRBF进行诊断。

为了进一步探究算法的诊断精度，将每一种故障的平均诊断结果列入表3。由表3可知：DAE-FRBF在每一种故障的诊断中都取得了最高的正确率，绝大部分都达到了98%；FRBF与DAE在进行诊断时，两者在除了故障5和6的其余故障中都取得了差不多的故障诊断正确率，而在故障5和6,FRBF都只取得了93%的正确率，与其他故障的诊断正确率相差颇大；SVM除了在故障1和10取得95%的诊断正确率之外，其余都与RBF一样正确率偏低。通过观察表中下面3种方法，它们都在诊断故障5和6时出现了正确率明显降低，RBF的诊断正确率甚至降到了90%以下。将10次试验对故障5和6的诊断错误样本进行统计，如图7所示。

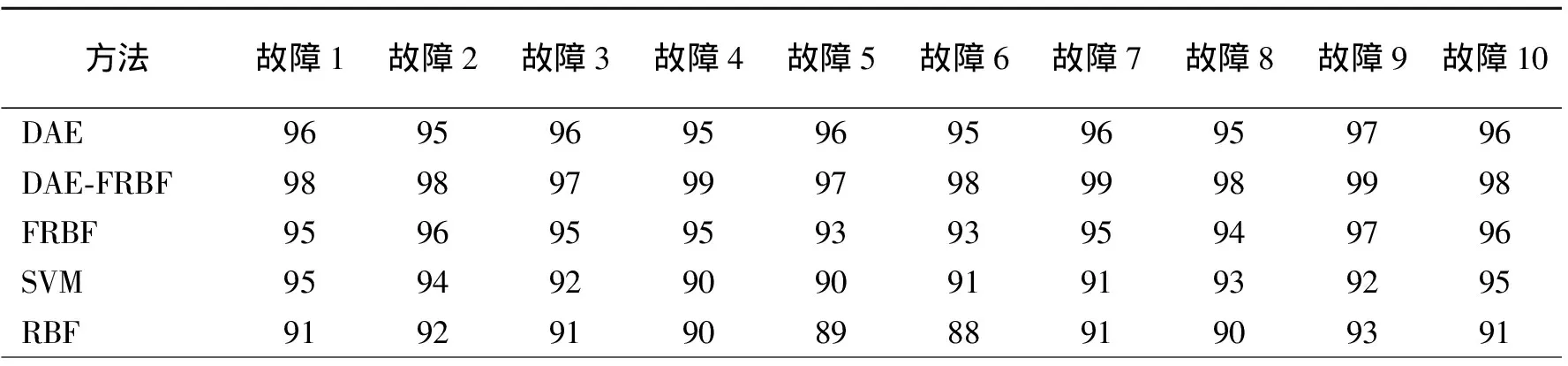
表3 各类故障平均诊断结果

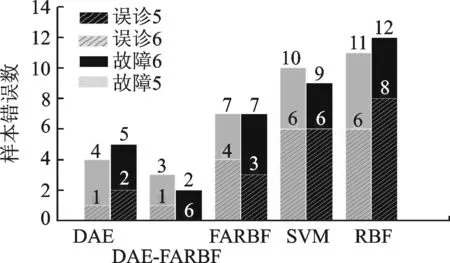
图7 故障5和6误诊图Fig.7 Misdiagnosed map for fault 5 and 6

由图7可知，故障5和6可以认为是相似故障，使用表3下面3种算法进行诊断时，无法准确判断出它们的类别，经常将故障5与6混淆。如使用SVM进行诊断时，在10次将故障5诊断错误中，有6次将其判断为故障6；在9次将故障6诊断错误中，也有6次将其判断为故障5。而使用前2种算法却能有效地将两者区分开来，在使用DAE-FRBF进行诊断时，将故障5误判为故障6仅有1次，甚至没有误判故障6为故障5。这是由于在面对相似故障，获取的传感器参数极其相似，使用传统的人工智能方法很难准确去判断。而DAE与DAE-FRBF在使用深度结构网络提取了深层特征之后，能够使用更利于分类的特征向量进行故障诊断，从而误诊率大大降低。

为了进一步检验算法的鲁棒性，对样本数据使用Matlab中的awgn函数添加高斯白噪声进行试验，信噪比值分别取40，35，30，25和20，使用上面的5种算法进对比，结果如图8所示。

图8 不同信噪比下的诊断正确率Fig.8 Diagnostic accuracy of different SNR

由图8可知，随着噪声加大，各个算法的正确率均有所下降， 其中SVM在噪声比例上升到一定程度时，正确率的下降斜率变得很大，这是由于SVM将加入的噪声当作正常参数进行了训练，产生了过拟合。RBF与FRBF同样在噪声的影响下，正确率有了较大幅度的下降。而DAE与DAE-FRBF由于使用降噪自编码器提取了更为鲁棒的特征，虽然正确率也有所下降，但影响较小，体现了良好的鲁棒性。

5 结 论

1) 通过降噪自编码器提取深层特征，获得了更容易进行故障诊断的特征向量，使用该特征向量DAE与DAE-FRBF较之其他方法拥有更高的诊断精度，在面对传统人工智能方法难以判别的相似故障也取得了良好的诊断结果，算法的诊断效果也相当稳定。

2) 通过降噪自编码器提取的特征不仅更利于分类，同时由于在进行无监督训练时就已经进行了噪声训练，其提取的特征具有较好的鲁棒，在对数据进行加躁后，相比其余几种方法，仍拥有较好的诊断精度。

3) 笔者提出的DAE-FRBF在原始DAE的基础上融入了FRBF。从诊断结果可以看出，FRBF较之RBF有了较大的提高，在除了故障5与6外诊断精度已经接近了DAE，拥有良好的分类性能。将其与DAE结合之后，DAE-FRBF在继承原有优点的基础上，诊断能力进一步提升，每一种故障都取得了最高的正确率，平均诊断正确率达到了98.1%，算法的稳定性也进一步提高。