外部激励对齿轮箱系统振动能量传递特性的影响
2019-06-24李淑颖
李淑颖 ,霍 睿,刘 玥
(1.山东大学机械基础实验教学中心,山东 济南 250061;2.山东大学机械工程学院,山东 济南 250061)
0 引言
齿轮箱系统振动噪声问题的研究,在20世纪50年代前,以啮合冲击作为描述和解释齿轮动态激励及动态响应的基础,最早是将齿轮传动系统简化为简单的单自由度系统。姚文席提出了单级齿轮传动的动态设计方法,建立了系统的动态弯曲-扭转模型[1];王建军研究了齿轮系统的转子耦合振动[2];S.Li,A.Kahraman 建立了考虑动态摩擦力的直齿轮传动模型,把轴承简化为阻尼和弹簧,同时采用弹性流体动力润滑的理论完成了动态摩擦力的计算[3-4]。随着振动相关理论趋于成熟,学者们不再简单地把齿轮传动系统简化处理,开始将其视为具有弹性的机械系统,以振动理论为基础,分析在各种因素影响下齿轮箱系统的振动特性[5-7]。
本文将齿轮箱系统视为具有弹性的机械系统,考虑外部激励和内部激励等多种影响因素,建立了齿轮箱板-轴承-轴-齿轮-轴-轴承-板的具有多自由度的非线性耦合系统动力学模型,并进行了数值求解,研究了外部激励对系统振动能量传递特性的影响。
1 齿轮箱系统的非线性动力学模型
在齿轮箱系统中,振动噪声的能量传播途径主要有结构声传播和空气声传播。在各种激励的作用下,齿轮回转产生振动,结构噪声由齿轮啮合点经过齿轮、轴、轴承和箱体最后传播到基座,振动传递的过程中会伴有噪声。空气噪声的传播途径有两个,一个是由齿轮啮合处传递到空气,另一个是由齿轮箱的箱体传播到外界空气[8-11]。对于齿轮箱而言,齿轮的啮合振动和其连带振动是整个系统振动噪声的主要来源。因此,本文只考虑固体振动的传播路径。齿轮箱系统振动能量传递路径如图1所示。
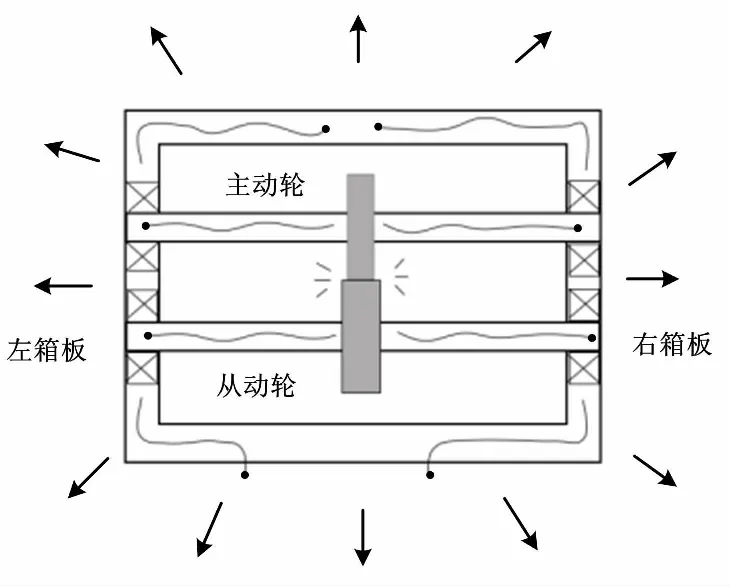
图1 齿轮箱系统振动能量传递路径
在此基础上,建立了板-轴承-轴-齿轮-轴-轴承-板的耦合系统动力学模型。将整个系统分为啮合齿轮、传动轴、轴承、齿轮箱体几个部分,分别建立各子结构的动力学模型。根据各子结构之间的约束关系和作用力,利用子结构综合法,建立了齿轮箱系统的动力学模型。
1.1 啮合齿轮弯扭耦合振动模型
啮合齿轮弯扭耦合模型可简化为由弹簧和质量块组成,其中弹簧忽略质量,质量块忽略弹性,所以可采用集中质量法建模。 齿轮啮合传动部分是其关键,啮合传动特性的影响因素较多,包括齿轮制造和安装误差、啮合冲击作用、时变啮合刚度的影响、齿侧间隙等。本文忽略了啮合冲击力的影响,建立如下模型:
J1θ1(t)+r1km(t)δ(t)+r1cg(εd-εs)=T1n(t)
(1)
J2θ2(t)+r2km(t)δ(t)+r2cg(εd-εs)=-T2n(t)
(2)
m1y1(t)+Fy1(t)+km(t)δ(t)+cg(εd-εs)=0
(3)
m2y2(t)+Fy2(t)+km(t)δ(t)+cg(εd-εs)=0
(4)
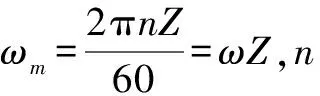
1.2 传动轴和箱体的振动方程
根据梁的弯曲振动理论,主动轴在垂直于z1方向的运动方程如式(5)所示:
(5)
式中:ρ(z1)为单位体积的质量;A(z1)为横截面积;E为弹性模量;J(z1)为轴的惯性矩;δ(z1)为脉冲函数。l11为主动轴左段的长度;l12为主动轴右段的长度。
假设传动轴为理想的弹性体,且轴的横截面在扭转振动中扔保持为平面作整体运动。设主动轴单位长度的转动惯量为I(x1),ρ为单位长度的质量,剪切弹性模量为G,截面的极惯性矩为Jρ(x1),θ′(z1,t)为z1截面的角位移,则主动轴的扭转振动方程为:
(6)
同理,可得到从动轴的振动方程。
齿轮箱箱体的横向振动简化为四边简支的矩形板的横向振动,左箱板和主动轴轴承之间的弯矩为Mxc11,左箱板和从动轴轴承之间的弯矩为Mxc12。在各弯矩的作用下,左箱板的Y方向振动方程如式(7):
(7)
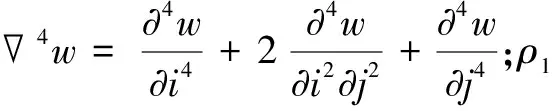
1.3 滚动轴承刚度计算
轴承是齿轮箱传动系统的关键组成部件,轴承支承刚度对齿轮箱系统的动力学性能有重要的影响。其令影响系统振动能量的传递。根据赫兹接触应力理论假设,滚动轴承刚度矩阵表示为[K]bm。根据刚度的定义,各方向的刚度系数分式为:
(8)
由上述刚度定义矩阵,可计算出轴承的多维刚度,深沟球轴承多维刚度值如表1所示。根据轴承的多维刚度和轴承的变形,可计算作用在轴承内圈和外圈的力和力矩。
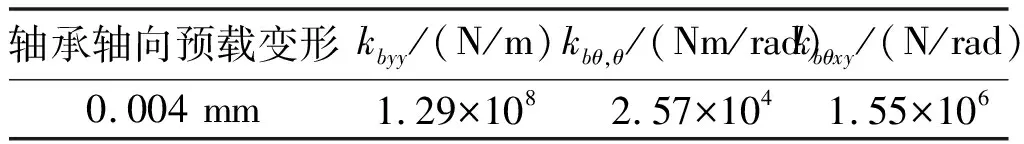
表1 深沟球轴承多维刚度值
根据轴承的多维刚度和其变形,可得作用在轴承内、外圈的力和力矩。其变形协调关系为:
(9)
(10)
(11)
(12)
在齿轮箱耦合振动的模型中,由于仅考虑轴和板弯曲振动的耦合,可令syc11=syc12=syc21=syc22=0。由轴承和轴之间的作用力的关系和变形协调关系,得主动轴左右两端的力和力矩计算表达式如下:
(13)
(14)
(15)
(16)
从动轴左右两端的力和力矩计算如式如下:
(17)
(18)
(19)
(20)
根据啮合齿轮、传动轴、齿轮箱板的振动方程和轴承变形作用力和力矩,联立方程组,可得到整个齿轮箱系统的动力学模型。
2 齿轮箱系统振动能量计算
振动传播的实质是振动能量的传播,其强度直接取决于振源输入能量的大小。在振动理论中,振动能量传递功率是指单位时间内外力做功,其反映了结构振动中的能量传递,给出了振动传输的绝对度量。振动能量传递功率是指一个振动周期内,激励力对振动系统输入能量的平均值,其描述的是一种时间平均能量传递[11]。对于具有周期的稳态运动,其平均振动能量传递P和瞬时能量传递具有如式(9)的关系:
(21)
式中:p(t)为瞬时能量传递;P为平均振动能量;T为运动的周期;r为任意的正整数。
由式(21)可见,当r趋近无限大时,振动能量传递值实质上是瞬时能量传递的数学期望。
齿轮啮合点瞬时耗散能量是啮合力与在啮合线方向上运动速度的乘积,其计算表达式为:
p1(t)=fv={cg[δd(t)-δs(t)]+km(t)δ(t)}[δd(t)-δs(t)]
(22)
式中:cg为啮合阻尼;km(t)为时变啮合刚度;δ(t)为关于侧隙的非线性函数;δd(t)为动态传递误差;δs(t)为静态传递误差。
主动轴a端轴承传递到箱板的瞬时振动能量pa1(t)表达式如式(23):
pa1(t)=Mxc11θxc11=Mxs11θxc11
(23)
从动轴a轴承传递到箱板的瞬时振动能量pa2(t)表达式如式(24):
pa2(t)=Mxc21θxc21=Mxs21θxc21
(24)
时间平均振动能量传递描述了激励力对系统输入的平均能量水平,振动和噪声的传播即是能量的传播,因此时间平均振动能量传递可用来衡量系统的振动噪声水平。求得以上各瞬时功率的时间平均功率,即可得到齿轮系统的能量传递。
3 非线性系统数学模型的求解
针对研究的齿轮箱系统的数学模型的特点,采用龙格-库塔法对系统振动方程求解。为方便使用龙格-库塔法,需要先将系统的动力学方程和振动能量传递方程离散化处理,表达为状态空间方程的形式。定义系统的状态变量如下:u1=F1,u2=F1,u3=F2,u4=F2,u5=Qy1,u6=Qy1,u7=Qy2,u8=Qy2,u9=φ1,u10=φ1,u11=φ2u12=φ2,u13=P1E(t),u14=Pa1E(t),u15=Pa2E(t)。
其中:F1和F2分别为主动轴和从动轴扭转振动各阶正则坐标组成的向量;Qy1和Qy2为主动轴和从动轴横向振动各阶正则坐标组成的向量;φ1和φ2为左箱板和右箱板横向振动各阶正则坐标组成的向量;p1E(T)、pa1E(t)、pa2E(t)分别为各瞬时功率的平均时间功率。
定义系统的状态变量,根据系统的振动方程和能量传递函数建立系统状态空间方程,采用龙格-库塔法并基于MATLAB,对系统的数学模型进行求解。
4 仿真分析
基于MATLAB对齿轮箱非线性系统进行数值仿真,分析外部激励对系统振动能量传递特性的影响。系统参数如下。
直齿轮模数为3,齿数为60,材料选取45#钢,弹性模量为19.5×1010Pa,泊松比为0.28,传动轴长度为0.8 m,惯性矩J为1.26×10-7m4,传动轴的剪切弹性模量为G=7.62×1010Pa,截面扭转的极惯性矩Jρ=2.5×10-7m4,单位长度的扭转惯量为I=1.946×10-3kg·m, 齿轮箱板材料为1020钢板,箱板密度ρc=7 870 kg/m3,箱板弹性模量Ec=2.05×1011Pa,箱板泊松比uc=0.28,箱板厚度为15 mm。梁的横向振动阻尼为34 N/(m/s),板的阻尼为20 N/(m/s),齿轮的啮合阻尼30 N/(m/s)。
时域内齿轮啮合点的耗散能量曲线如图2所示。主动轮转速为n1=1 000 r/min,时域内齿轮啮合点的时间平均振动能量传递,主动轮转速为n1=1 000 r/min,受状态变量导数初值的影响啮合振动能量传递在t为0时刻的数值很大。系统进入稳定状态后,啮合开始后5 s系统啮合功率流为10 W,随时间推迟啮合振动能量趋于稳定值。
时域内左箱板时间平均振动能量传递曲线如图3所示。系统进入稳定状态后,主动轴传递到左箱板的时间平均振动能量趋近于6×10-3W。
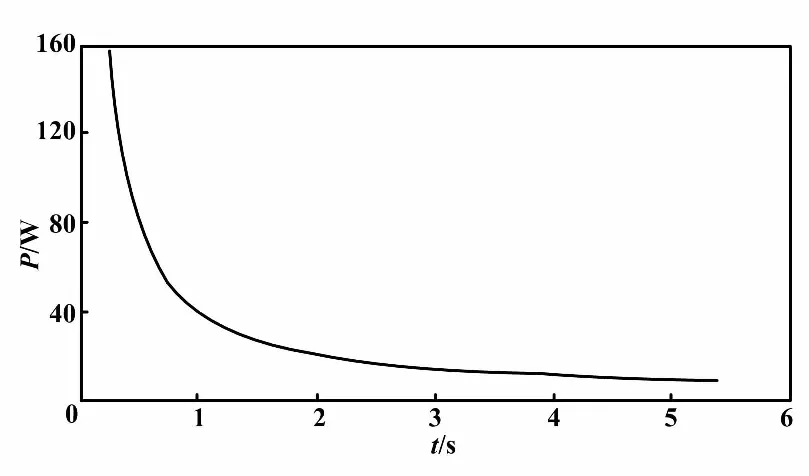
图2 时域内齿轮啮合点的耗散能量曲线
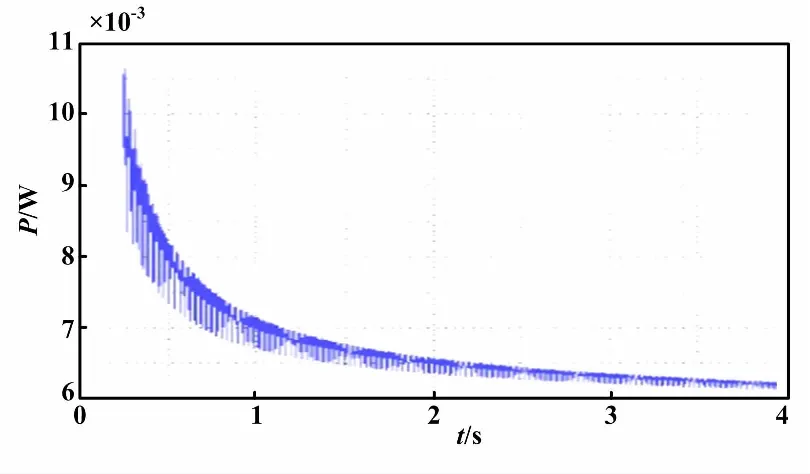
图3 时域内左箱板时间平均振动能量传递曲线
图4描述了外部激励T1的角频率为100 rad/s时,齿轮啮合振动能量传递随频率的变化情况。在低频时,系统的振动能量传递波动较大;在中低频范时,系统振动能量传递值稳定在0.046 W。而后啮合振动能量传递增大,在420 Hz处达到峰值,峰值过后随着频率的增大振动能量传递值迅速减小,最后趋于稳定值。
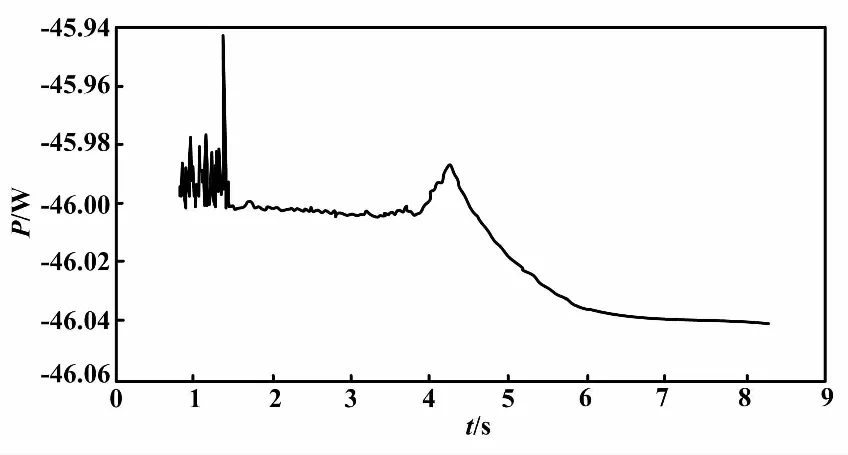
图4 齿轮啮合点的耗散能量曲线(角频率为100 rad/s)
图5描述了外部激励T1的角频率为100 rad/s时主动轴传递到左箱板的时间平均振动能量曲线。在低频段,系统振动能量传递波动较大;在中低频段和高频段,系统振动能量趋于稳定值,但在峰值处系统振动表现出复杂特性。
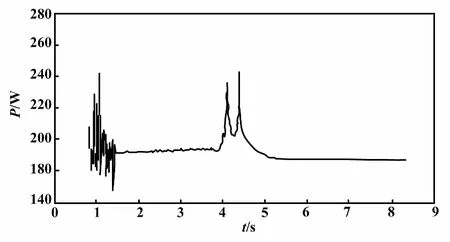
图5 左箱板的时间平均振动能量曲线(角频率为100 rad/s)
齿轮啮合点的耗散能量曲线能量曲线如图6所示。当外部激励T1的角频率增大到300 rad/s时,齿轮啮合振动能量传递曲线形状与外部激励角频率为100 rad/s时相似,但在整个频率范围内,系统振动能量传递值均减小。
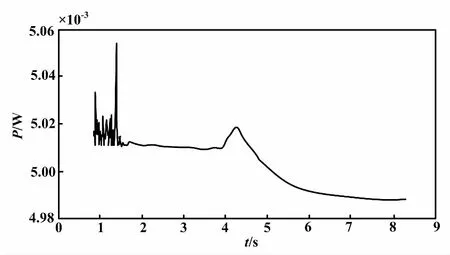
图6 齿轮啮合点的耗散能量曲线(角频率为300 rad/s)
左箱板的时间平均振动能量曲线如图7所示。当外部激励T1的角频率增大到300 rad/s时,在整个频率范围内,主动轴传递到左箱板的时间平均振动能量值均减小,但振动能量峰值仍出现在420 Hz左右。
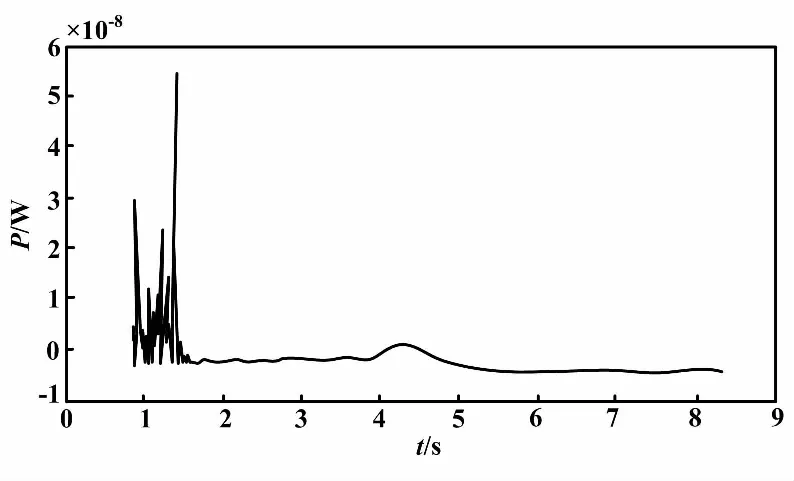
图7 左箱板的时间平均振动能量曲线(角频率为300 rad/s)
由于仿真的齿轮箱非线性系统具有对称性,主动轴传递到右箱板的时间平均振动能量与传递到左箱板相同,在此不再赘述。
5 结束语
本文建立了板-轴承-轴-齿轮-轴-轴承-板的齿轮箱非线性耦合系统动力学模型,应用振动功率流理论推导了系统振动能量传递计算公式;将系统动力学模型离散化,建立了系统的状态空间方程,提出了非线性耦合系统的数值求解方法。基于MATLAB,对系统的振动特性进行了仿真分析,研究了外部激励对系统的振动能量传递特性的影响。在时域范围内,齿轮啮合振动能量耗散和主从动轴传递到箱板的振动能量随时间推移趋于一稳定值;在频域范围内,当外部激励为正弦激励时,低频段振动波动较大,中频段出现峰值,中高频系统振动趋于稳定。随着正弦激励角频率的增大,系统振动能量传递在整个频域范围内减小。该研究为齿轮箱的振动噪声主动控制提供理论依据,具有一定的理论和实践价值。
