云模型控制器在两轮自平衡机器人中的应用

徐子为，李 众

(江苏科技大学电子信息学院，江苏 镇江 212003)

0 引言

两轮自平衡机器人系统本质上是一种极其不稳定的欠驱动系统。国内外专家学者对于该类机器人的控制都进行了较为深入而广泛的研究。首要研究课题便是平衡控制。大量文献主要从传统控制、现代控制、智能控制三个方向对其平衡系统进行研究[1-9]。控制方法主要有比例积分微分控制器(proportion integral derivative,PID)、线性二次型调节器(linear quadratic regulator,LQR)、模糊算法等，但是控制效果始终不理想，机器人抖动现象严重。

本文将两轮自平衡机器人平衡系统作为研究对象，通过一维云模型多规则推理映射算法，分别设计了三规则以及五规则云模型控制器。将两种云模型控制器分别应用于两轮自平衡机器人平衡控制系统，并在实际应用中进行了对比分析。通过试验，证明了云模型控制器的可行性与科学性。

1 两轮自平衡机器人平衡系统

主控制器、动力驱动以及姿态传感器是两轮自平衡机器人平衡系统的重要组成部分。其中，主控制器单元由STM32最小系统板和云模型控制器组成。姿态传感器可以较为精准地计算两轮自平衡机器人的俯仰角θ。图1为两轮自平衡机器人平衡系统示意图。当θ=0时，表示机器人处于直立姿态；当θ>0时，表示两轮自平衡机器人向右倾斜，并且向右移动；当θ<0时，机器人向左倾斜，并向左运动。设eθ为机器人俯仰角和机器人直立时角度差，即eθ=θ-0，eθ与机器人运动速度相关联。平衡系统通过控制器控制改变车轮速度，实现对两轮自平衡机器人的平衡控制。

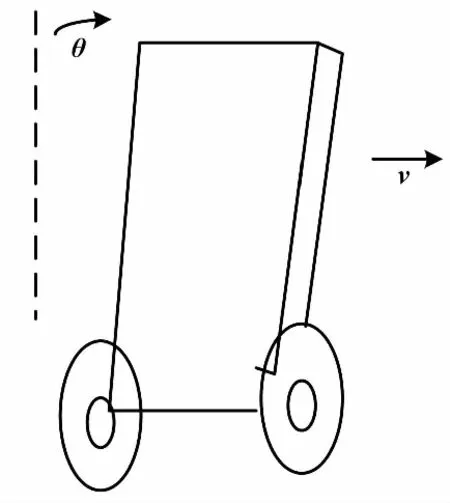
图1 两轮自平衡机器人平衡系统示意图

2 硬件系统设计

2.1 主控制器

本系统选择STM32F103C8T6作为主控制器。STM32F103C8T6拥有ARM Cortex-M3 32位的内核，以及众多的外设模块。该芯片主要负责采集传感器数据，根据采集的俯仰角信息，通过云模型算法驱动电机模块来维持机器人的平衡。

2.2 姿态传感器

选取数字传感器MPU6050作为姿态传感器。该传感器内置加速计和陀螺仪。主控制器通过I2C总线获取机器人的姿态信息，并通过卡尔曼滤波算法保证数据的准确性。本系统的关键在于实现对两轮自平衡机器人俯仰角信息的采集。主控制器通过俯仰角与平衡直立时角度0°的误差对电机作出相应的控制。

2.3 电机驱动模块

选取TB6612FNG作为电机驱动模块。该芯片可以同时驱动两组直流电机，并且可以通过配置输入输出口电平，实现对直流电机转动方向和转速等的控制。当两组直流电机被同时控制时，两轮自平衡机器人直立、后退、前行以及转弯等运动就可以被精准控制。

3 软件系统设计

3.1 MPU6050通信设计

数字传感器MPU6050与主控制器采用I2C总线进行通信。I2C是一种串行通信方式。I2C总线有两根总线，一根为SDA，另一根为SCL，分别用于传输数据信号和时钟控制信号。MPU6050获取数据主要有以下3个步骤，首先是设置数字传感器MPU6050，接着是写入传感器地址和内部地址，最后读取传感器数据。姿态传感器通信流程如图2所示。MPU6050模块采用卡尔曼滤波和姿态解算技术，通过串口便可直接读取三轴的角度信息，并且读取的角度误差小、精度高。

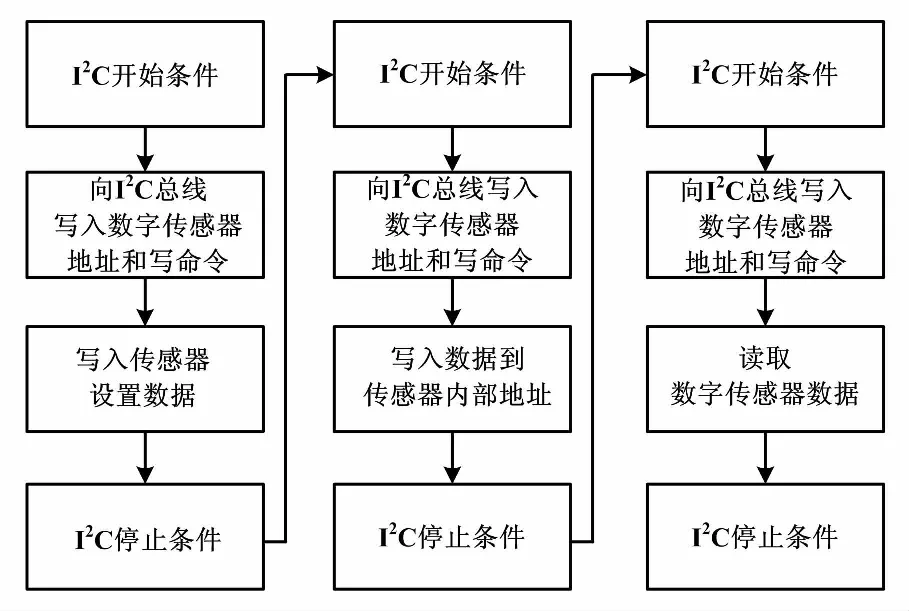
图2 姿态传感器通信流程图

3.2 电机驱动设计

本文电机驱动器件采用日本东芝半导体公司生产的TB6612FNG。图3为该驱动芯片内部原理图。

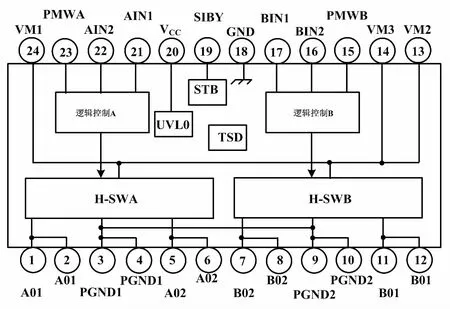
图3 驱动芯片内部原理图

该芯片内置两组H桥驱动电路和两组逻辑控制单元，可通过单片机同时控制两组直流电机。PWM、IN1、IN2与主控制器一组I/O口相连接，单片机通过控制IN1、IN2电平高和低就可实现对电机正反转方向的控制。主控制器输出脉冲可调的脉冲宽度调制(pulse width modulation,PWM)方波到驱动芯片TB6612FNG，实现对电机转速的控制。表1为该驱动芯片的逻辑真值表。主控制器参照该表，控制I/O口高低电平实现控制电机正反转等功能(CW表示正转，CCW表示反转)。

表1 逻辑真值表

3.3 云模型控制器设计

云模型控制系统的优点：一是能够抑制非线性因素影响；二是对于被控对象数学模型的准确性要求不高，并且鲁棒性较强。量化因子、推理映射、驱动因子是云模型控制器的3个主要组成部分。

一般情况下，设计云模型控制器有以下几个步骤[10-15]。

①首先，需要明确输入变量、输出变量的归一化。

②其次，要确定合适云化方法以及相关规则推理。

③再次，设计云模型映射器的映射关系。

④最后，选择适宜的输入以及输出变量论域，并且得出云模型控制器的特性参数。

在本文的平衡系统中，两轮自平衡机器人通过姿态传感器MPU6050获取俯仰角θ。该角度即反映机器人的平衡姿态。系统对体现姿态的俯仰角θ与两轮自平衡机器人处于平衡状态时的角度0°的误差eθ，进行量化因子归一化处理，将处理后的数据作为云模型映射器的定量输入。通过云模型规则推理映射出定量的输出值。该值经过驱动因子转化为电机脉宽的校正量。将该脉宽校正量与电机零点脉宽之和作为输出量给电机驱动TB6612FNG,对电机进行控制，从而实现两轮自平衡机器人的平衡控制。云模型控制器系统框图如图4所示。

图4 云模型控制器系统框图

经过理论分析与控制系统特性研究，结合多次试验验证，能够得出多条两轮自平衡机器人的平衡规则。采用一维云模型多规则映射算法，实现对两轮自平衡机器人的平衡控制。经过定性分析，得出云模型控制规则可以用如下语言简单描述：

IFeθ负大 THEN 电机校正变量负大

IFeθ零 THEN 电机校正变量零

IFeθ正大 THEN 电机校正变量正大

使用云模型，可以将以上比较模糊的语言所要表达的内容转变成对被控对象的定性分析。在此基础上，结合系统特性以及一定的控制经验，在不断的试验验证的基础上，得出如表2所示的三规则控制云参数。

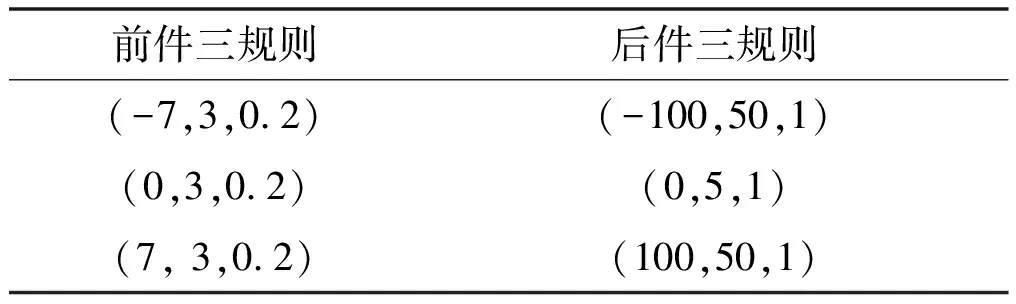
表2 三规则控制云参数

图5和图6分别表示表2中三规则云参数的前件云和后件云。

图5 三规则前件云

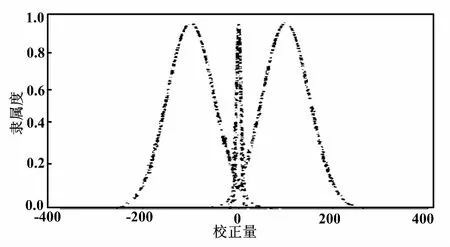
图6 三规则后件云

依据一维云模型多规则映射算法，可以得到如图7所示的一维云模型三规则映射关系图。

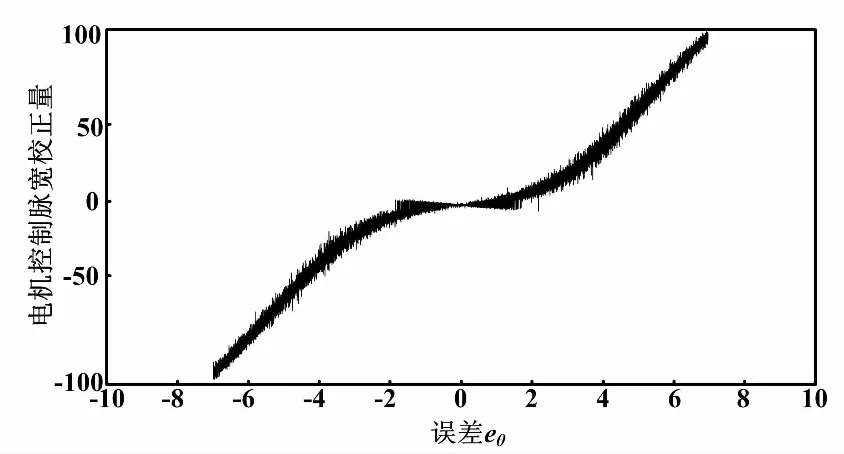
图7 一维云模型三规则映射关系图

同理，根据控制系统特性和人的控制经验得到云模型五规则系统控制规则。其表现为:

IFeθ负大 THEN 电机校正变量为负大

IFeθ负小 THEN 电机校正变量为负小

IFeθ零 THEN 电机校正变量为零

IFeθ正小 THEN 电机校正变量为正小

IFeθ正大 THEN 电机校正变量为正大

表3给出了云模型五规则的推理映射云参数。

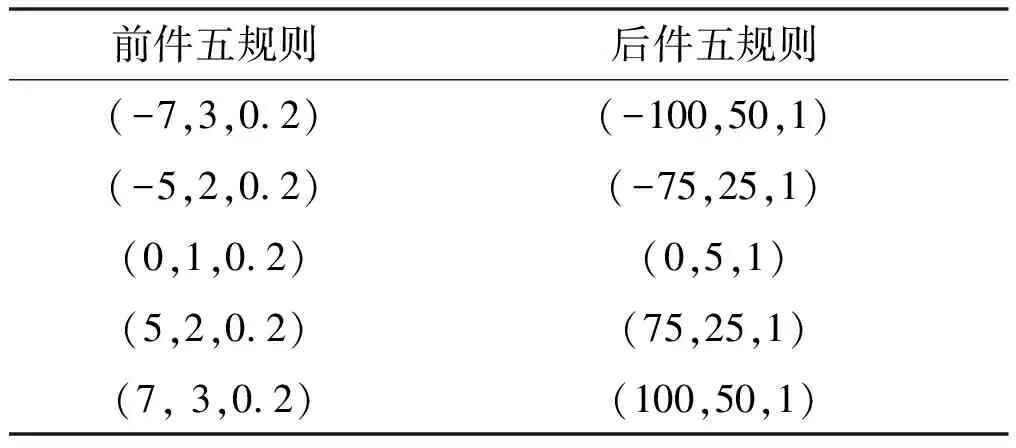
表3 五规则控制云参数

五规则情况下的前件云和后件云分别如图8、图9所示。一维五规则映射推理、三规则与五规则推理比较曲线分别如图10、图11所示。

通过试验分析，本文分别将一维云模型控制器的三规则推理的映射关系和五规则推理的映射关系进行了对比。由图11可以看出，当俯仰角的角度误差eθ∈[-2,2]时，三规则推理的映射没有产生响应，给出的脉宽校正量大约为0。而同样角度误差eθ∈[-2,2]时，却能刺激五规则推理，由五规则推理映射关系可以看出，直流电机产生了一个范围[-20,20]的非线性的校正脉宽量映射。由图11分析可得知：当机器人俯仰角波动较大时，通过五规则推理出的映射曲线电机校正值显然要大于三规则推理得到的值，表五规则推理的响应速度表明显比三规则推理要来的快。根据控制经验，上述试验分析得到的五规则映射推理结果更加符合人的控制思维。

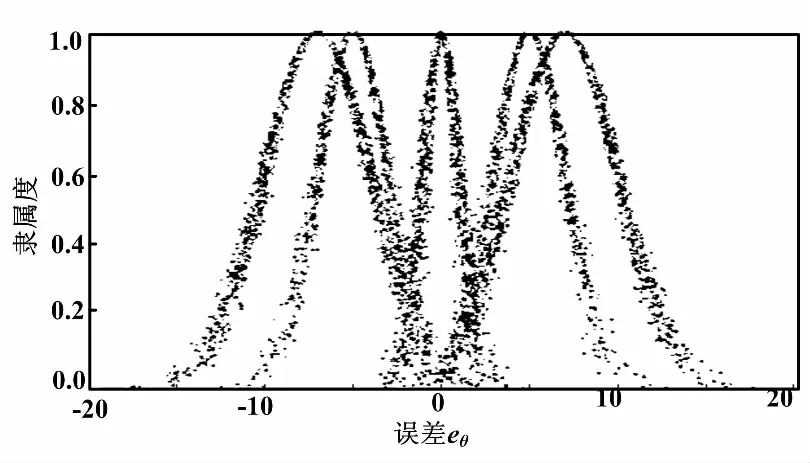
图8 五规则前件云

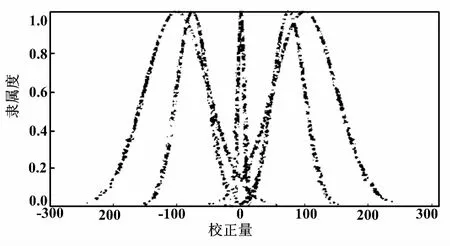
图9 五规则后件云

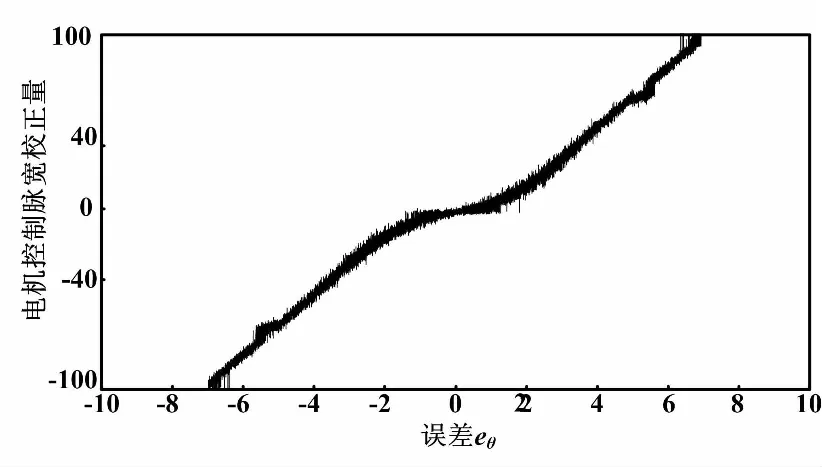
图10 一维五规则映射推理图

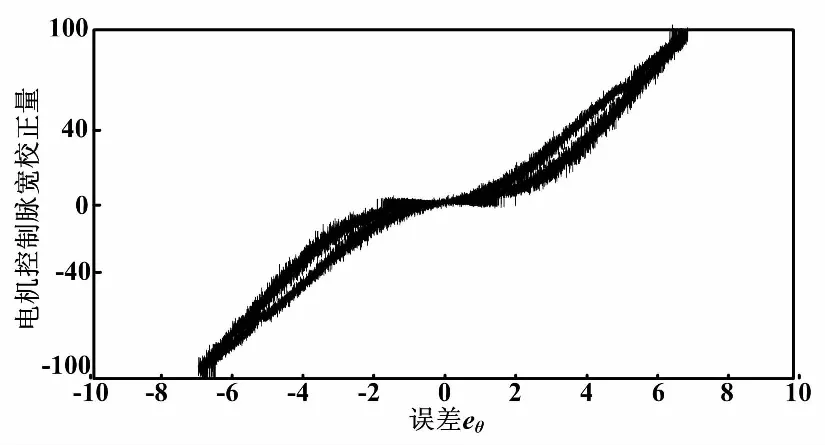
图11 三规则与五规则推理比较曲线

4 试验数据分析

基于一维云模型控制器的两轮自平衡机器人，能够很好地实现直立动态平衡。当系统遭遇外界扰动时，两轮自平衡机器人会自动调整，保持直立平衡的姿态，实现动态平衡。

使用串口助手工具，对最能体现其直立平衡特性的俯仰角进行了实时监测。从宏观角度进一步分析实时监测到的数据，可以得出这样的结论：两种云模型控制器都能够让两轮自平衡机器人在相当长的时间保持直立特性，并且能够在较小的角度范围内稳定保持平衡。

对比分析使用三规则和五规则一维云模型控制器的实时检测曲线数据可以得出，在直立平衡方面，五规则云模型控制器性能更优。在外界强干扰和主动冲击条件下，即两轮自立平衡机器人的俯仰角度出现大波动的情况下，五规则云模型控制器具有更好的系统特性，能够以更快的收敛速度，在更短的时间内再次保持平衡。

5 结束语

本文主要研究对象为两轮自平衡机器人平衡系统。根据该控制系统特征，分别研究设计了一维三规则、五规则云模型控制器。分别采用对比分析与试验验证的方法，得出结论：相较于三规则云模型控制器，五规则云模型控制器性能更优，控制效果更佳。

作为一个具有非线性、强耦合性和多变量的控制系统，两轮自立平衡机器人平衡系统的实时控制规律也呈现着多变性，难以被人掌握。云模型智能控制器的出现，大大提升了对两轮自平衡机器人的控制效果。不仅如此，云模型控制器对两轮自平衡机器人出现的高频抖动问题也有所改善。

云模型理论在不断完善和发展，向着智能控制方向发展的趋势也日趋明显。本文对云模型控制器在硬件平台实现的可行性和科学性进行了验证，这也为后续云模型控制器的研究设计提供了参考。