砂粒对河水中氨氮的吸附及参数拟合

拦继元，卫旭琴，杨林

(青海师范大学 化学化工学院，青海 西宁 810008)

固态颗粒状物质，如粒径不一的各种沙石、石英砂和河沙等，因其自身具有较大的比表面积，当水流过固态颗粒时，水中所携带的各种物质会被或多或少地吸附在颗粒物质的表面和内部，从而起到吸附水中杂质的作用[1]，其吸附效果受吸附剂性质、吸附质性质、共存物质、接触时间等多种因素的影响[2]。氨氮是指水中以游离氨(NH3)和铵离子(NH4+)形式存在的氮，广泛存在于河流、湖泊等地表水及地下水中，是一种典型的水体污染物。目前，国内关于氨氮的吸附研究主要集中于2方面：一方面，采用不同的吸附剂，如沸石、活性炭、麦饭石、蛭石、陶粒、煤渣、页岩、砾石、黏土、各种湿地填料及生物碳来研究这些材料对氨氮的吸附效果[3-18]；另一方面，新型技术对氨氮吸附的研究[19-22]。然而，已有的研究中关于砂粒对氨氮吸附的研究并不多见。为此，以自然界中广泛存在的砂粒作为吸附剂，选取青海省西宁市文化公园内的湟水河河水作为试验水样，开展砂粒对氨氮的等温吸附试验、吸附动力学试验及吸附热力学试验，得到相应的试验结果，利用朗缪尔吸附(Langmuir)、Freundlish和BET这3种经典的吸附等温模型，以及准一级、准二级吸附动力学模型和吸附热力学Van’t Hoff方程对砂粒吸附氨氮的过程进行参数拟合，并对所得参数的意义进行分析，为丰富和发展砂粒对氨氮的吸附研究提供参考依据。

1 材料与方法

1.1 材料

吸附剂砂粒，取青海湖边的天然砂粒作为吸附剂，将砂粒洗干净后分别过20目和40目筛，使砂粒粒径在0.35～1.2 mm。

取湟水河的河水作为试验水样，取样点位于青海省西宁市城西区文化公园内。

1.2 方法

参照GB 7479—87中的纳氏试剂比色法测定氨氮浓度。

吸附等温线试验方法：称取9份砂粒，每份100 g，分别倒入250 mL的具塞锥形瓶中。通过向河水水样中添加不同体积的氨水，得到8份不同氨氮浓度的河水水样，各抽取100 mL不同浓度的水样分别加入到装有砂粒的8个具塞锥形瓶中，另取一个锥形瓶加入去离子水，作为空白样品(CK)。将所有具塞锥形瓶放置在恒温摇床上，120 r·min-1、(25±1)℃振荡24 h，取锥形瓶中溶液测定其氨氮浓度，计算砂粒对氨氮的吸附量。

吸附动力学试验方法：称取砂粒100 g，倒入250 mL具塞锥形瓶中，加入100 mL河水水样，测定水样中的氨氮初始浓度。准备与之相同的样品数份，将所有锥形瓶放置在恒温摇床上，120 r·min-1、(25±1)℃条件下振荡，每隔一段时间，测定溶液中氨氮的浓度。

吸附热力学试验方法：称取砂粒100 g，倒入250 mL具塞锥形瓶中，加入100 mL河水水样，测定水样中的氨氮初始浓度。准备与之相同的样品3份，分别在293、303和313 K的温度条件下120 r·min-1振荡24 h，取锥形瓶中溶液测定其氨氮浓度值，计算不同温度条件下砂粒吸附氨氮的热力学平衡常数。

1.3 吸附模型

吸附量计算公式：

q=V(ρ0-ρ)÷M。

式中：q为砂粒吸附量，mg·kg-1；ρ0为初始氨氮浓度，mg·L-1；ρ为吸附平衡后溶液中的氨氮浓度，mg·L-1；V为溶液体积，L；M为砂粒用量，kg。

Langmuir吸附等温线模型：

q=abρ÷(1+aρ)。

式中：q、ρ含义同上；a为吸附平衡常数，L·mg-1；b为单位吸附剂的饱和吸附量，mg·kg-1。

Freundlish吸附等温线模型：

q=Kρ1/n。

式中q、ρ含义同上，K、1/n皆为常数。

BET吸附等温线模型：

q=VmAmρ÷(ρs-ρ)÷[1+ρ(Am-1) ÷ρs]。

式中：q、ρ含义同上；ρs为饱和浓度，mg·L-1；Vm和Am分别表示单分子层吸附时的最大吸附量和与吸附能量有关的常数。

准一级吸附动力学模型：

qt=qe(1-e-k1t)。

式中：qe表示平衡吸附量，mg·kg-1；qt表示时间为t时的吸附量，mg·kg-1；k1表示一级吸附速率常数，h-1。

准二级吸附动力学模型：

qt=k2qe2t÷(1+k2qet)。

式中：qe、qt含义同上；k2表示二级吸附速率常数，h-1。

吸附热力学Van’t Hoff方程：

lnKd=ΔS/R-ΔH/(RT)。

式中：T为绝对温度，K；ΔS为熵变，J·mol-1·K-1；ΔH为焓变，J·mol-1；R为理想气体常数，取值为8.314 J·mol-1·K-1；Kd为热力学平衡常数，无量纲。

2 结果与分析

2.1 吸附等温线试验结果及非线性参数拟合

按照吸附等温线试验方法，得到砂粒对氨氮的吸附试验结果，带入Langmuir、Freundlish和BET吸附等温线模型中，利用Origin软件中的非线性自定义拟合功能，对这3种模型中的参数进行非线性拟合，3种模型的拟合曲线及参数见图1～3，参数汇总见表1。

图1 Langmuir模型拟合曲线及特征参数

图2 Freundlish模型拟合曲线及特征参数

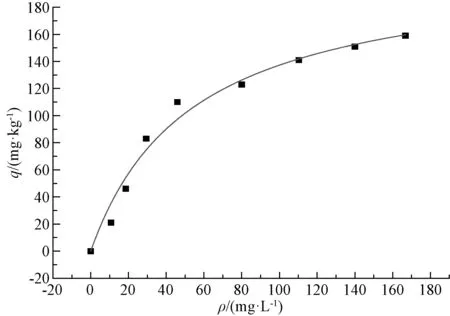
图3 BET模型拟合曲线及特征参数

表1 砂粒吸附氨氮的吸附等温模型及拟合参数

从图1～3可以看出，吸附初期砂粒对氨氮的吸附量增加较快，当砂粒的吸附量达到110 mg·kg-1以后，吸附量的增加值变小，拟合曲线趋于平缓。从表1可以看出，3种拟合模型中Freundlish模型的决定系数最小，而Langmuir和BET模型的决定系数较大。对比图1～3可以看出，在吸附初期，Langmuir和BET拟合曲线与真实的试验数据尚有一些差距，但到了吸附后期，Langmuir和BET拟合曲线与试验数据几乎重叠到一起。由此可以看出，Langmuir和BET模型能更好地表征砂粒对氨氮的吸附过程。从Langmuir模型拟合的参数可得，吸附平衡常数a=0.018 7>0，说明反应可自发进行，即砂粒可自行吸附河水中的氨氮；从Freundlish模型拟合的参数可得n=2.051 8，则1/n=0.487 4，在0.1～0.5，说明吸附较容易自发进行[2]。

2.2 吸附动力学试验结果及非线性参数拟合

按照吸附动力学试验方法，得到砂粒对氨氮的吸附动力学试验结果。利用Origin软件绘制氨氮浓度随时间的变化关系，见图4；利用Origin软件中的非线性自定义拟合功能，对准一级和准二级吸附动力学模型进行参数拟合，拟合曲线分别如图5、6所示，拟合参数汇总见表2。

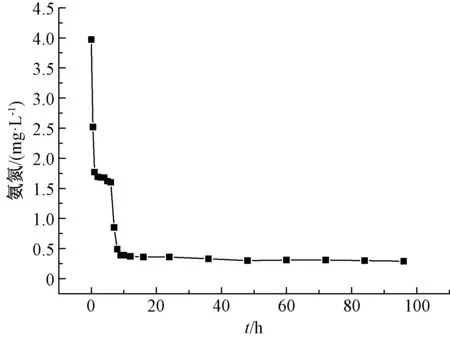
图4 氨氮浓度随时间的变化

图5 准一级动力学模型拟合曲线及特征参数

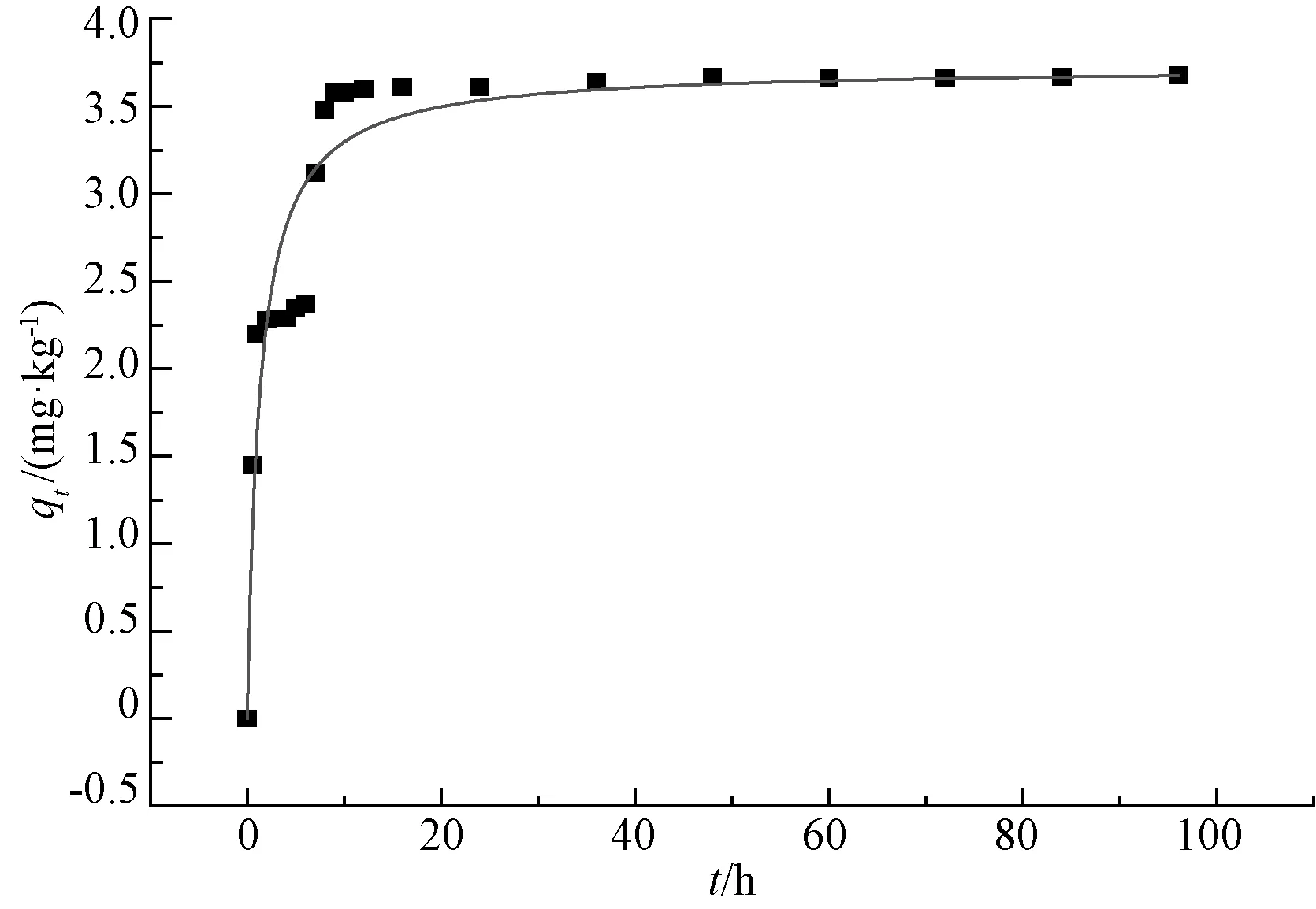
图6 准二级动力学模型拟合曲线及特征参数

从图4可以看出，氨氮浓度值在前期降低得非常迅速，但在12 h后降速明显减慢，48 h后趋于稳定。从图5、6也可以看出，氨氮的qt值在48 h以后趋于稳定。试验得出的平衡吸附量qe(96 h)值为3.68，准一级动力学模型拟合出来的值为3.561 1，与试验值相对误差为3.23%；准二级动力学模型拟合出来的值为3.726 0，与试验值相对误差为1.25%。准二级动力学模型拟合的决定系数值为0.884 7，高于准一级模型的0.803 4。对比图5、6也可看出，准二级动力学模型的拟合曲线更加接近qt曲线，说明准二级吸附动力学模型比准一级吸附动力学模型更符合本试验结果。

表2 2种吸附动力学模型的拟合参数

2.3 吸附热力学试验结果及参数拟合

吸附热力学试验结果及拟合参数见表3。在293、303、313 K温度下，ΔG均为负值，从吸附热力学的角度说明该吸附反应可自发进行，这也与前述试验结果一致。砂粒吸附氨氮的Van’t Hoff方程及线性拟合见图7，通过线性拟合可得Van’t Hoff方程的斜率和截距，经过计算得出ΔH=-13.02 kJ·mol-1，为负值，说明砂粒对氨氮的吸附为放热过程。同理可得ΔS=-23.34 J·mol-1·K-1，也为负值，说明吸附过程降低了固液界面的混乱度。原因可能是，吸附前溶液中的三维状态变成了吸附后固液界面的二维状态，所以熵值减小。

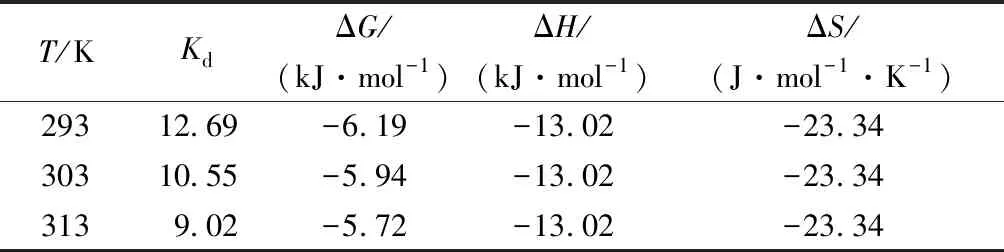
表3 吸附热力学试验结果及拟合参数

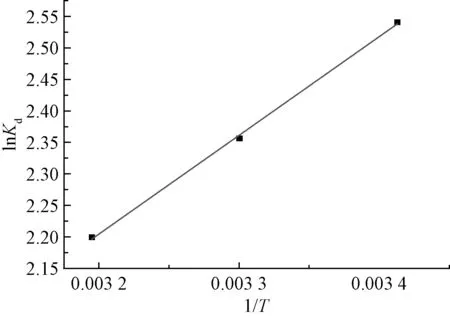
图7 砂粒吸附氨氮的Van’t Hoff方程及线性拟合

3 小结

本研究表明， Langmuir和BET模型用于拟合砂粒对水体氨氮的吸附时决定系数较大，与试验数据也较为接近，能较好地描述砂粒对氨氮的吸附过程。Langmuir模型中吸附平衡常数a=0.018 6>0，说明吸附可自发进行，即砂粒可自行吸附河水中的氨氮。Freundlish模型中参数n=2.051 8，说明吸附容易进行，吸附效果较好。准二级吸附动力学模型拟合出的平衡吸附量值与试验所得值更接近，其相关系数值也高于准一级吸附模型，说明准二级吸附动力学模型比准一级吸附动力学模型更加符合试验结果。由吸附热力学试验结果可知：砂粒吸附氨氮的ΔG为负值，说明吸附可自发进行；ΔH为负值，说明吸附反应为放热过程；ΔS为负值，说明吸附过程降低了固液界面的混乱度。