遗传算法优化的碳纤维复合材料声发射数据聚类分析
2019-06-24
(西北工业大学 动力与能源学院,西安 710072)
碳纤维复合材料具有质量小、强度高、抗热冲击性好、比重小等优点,广泛应用于航空航天、汽车制造、风电等领域。碳纤维复合材料在服役过程中,由于疲劳损伤、撞击、摩擦、振动等因素的影响,易产生基体开裂、纤维断裂、基体断裂等损伤,这些损伤会降低材料和构件的强度,直接影响到复合材料构件的完整性、安全性以及使用寿命,因此准确预测碳纤维复合材料缺陷的损伤形式,设计出合理的解决方案,具有重要的现实意义。
目前,碳纤维复合材料的损伤检测主要有红外热波检测、超声检测、扫描电子显微镜检测、声发射检测等,其中声发射检测是一种被动检测方式,其利用材料在局部受力的作用下会产生能量的快速释放而发出瞬态弹性波的特征,通过对弹性波记录的分析,来揭示材料内部受力作用下的变形、裂纹形成与裂纹扩展、断裂等现象。声发射检测方法不受材料加工形状及表面结构的影响,可以在线实时监测,不影响设备的运行,已经成为复合材料损伤分析中一种重要的分析工具。
声发射检测按照信号处理特点可分为特征参数法和全波形检测法两种,特征参数法就是将材料声发射时域波形信号简化为一些特征参数的记录,全波形法就是采集整个声发射过程中的波形数据。全波形分析方法可以观察到整个声发射事件的波形数据,可以对声发射事件进行局部分析,然而数据量大,处理复杂;参数分析方法就是通过对声发射全波形数据进行简化,通过事件计数、振铃计数、能量、幅度、持续时间、上升时间等参数来分析事件的特征属性。声发射参数分析方法具有数据量小,处理简单等特点,现在仍广泛使用。为此,对声发射参数数据进行分析,揭示损伤过程中材料的变化规律,具有重要的现实意义。
由于声发射事件的特征参数有数十个之多,在对信号进行聚类分析时,参数之间存在一定的相关性,所以需要对数据的特征进行优化,以提高建模速度以及识别效率。童小燕等[1]在对2D-C/SiC进行拉伸损伤检测的过程中,利用经验选择了声发射数据的上升时间、振铃计数、能量、持续时间、幅值、平均频率作为声发射事件的特征属性。王旭[2]在对聚乙烯自增强复合材料损伤模式的识别研究中,在声发射(AE)参数选择上以属性的相似性为度量指标,通过其划分模式的类别。栗丽[3]在对2D及3D纺织结构复合材料损伤机制的分析过程中,采用拉普拉斯分值和相关分析的特征选择方法,选择出具有较高分类能力及表征声发射信号的属性,最终从9个属性中选择4个,实现了数据的降维。
近年来,随着人工智能的快速发展,人们开始采用神经网络对数据进行建模,利用训练好的模型对未知数据进行分类判定。但是当数据的维数比较多,且维数之间不相互独立时,会使得神经网络出现过拟合,而造成所建模型精度变低,训练时间变长等问题。为了解决以上问题,笔者采用遗传算法优化对声发射数据降维,通过遗传算法将数据中起主要影响因素的属性筛选出来。
1 试验过程
1.1 材料与试样
选择日本东丽公司生产的T300型环氧树脂基碳纤维复合板,铺层结构为斜纹编织而成,纤维体积含量约为40%,用排水法测得样品体密度为2.18 g·cm-3,孔隙率约为13%。试件的形状尺寸参见GB/T 1447-2005《纤维增强塑料拉伸性能试验方法》中II型试样型式来制备,试件尺寸规格如图1所示。为防止样品被试验机夹头压碎,在试验样品的两端贴有硬铝加强片。
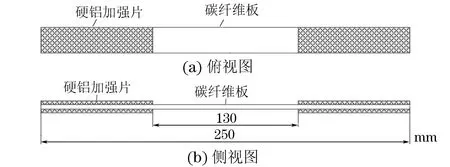
图1 碳纤维板拉伸试样的尺寸规格
1.2 试验方法与结果
试验时,在传感器表面涂上一层硅脂,使其与被测物表面紧密接触,增加弹性波的接收。由于碳纤维板不可以与磁性夹具牢固吸附,所以通过橡皮筋将声发射传感器固定在碳纤维板上。声发射仪采用北京声华的SAEU2S声发射系统,其中声发射仪前置放大器增益为40 dB,信号门槛值设置为40 dB,采样频率设置为4 MHz,传感器频率设置为40 kHz~400 kHz,采用一个通道来记录整个声发射事件。试验采用参数数据分析方法,所要测量的参数有幅度、振铃计数、持续时间、能量、上升计数、上升时间、有效电压(RMS)、平均信号电平(ASL)、质心频率、峰值频率共计10个量,其中序号、通道号信号到达时间等参数不包括在内。拉伸试验在Instron5567电子万能试验机上进行,试验以3 mm·min-1的加载速度进行拉伸直至试件断裂,采集拉伸过程中的声发射信号以及应力计的测量值,试样的应力-应变曲线如图2所示。
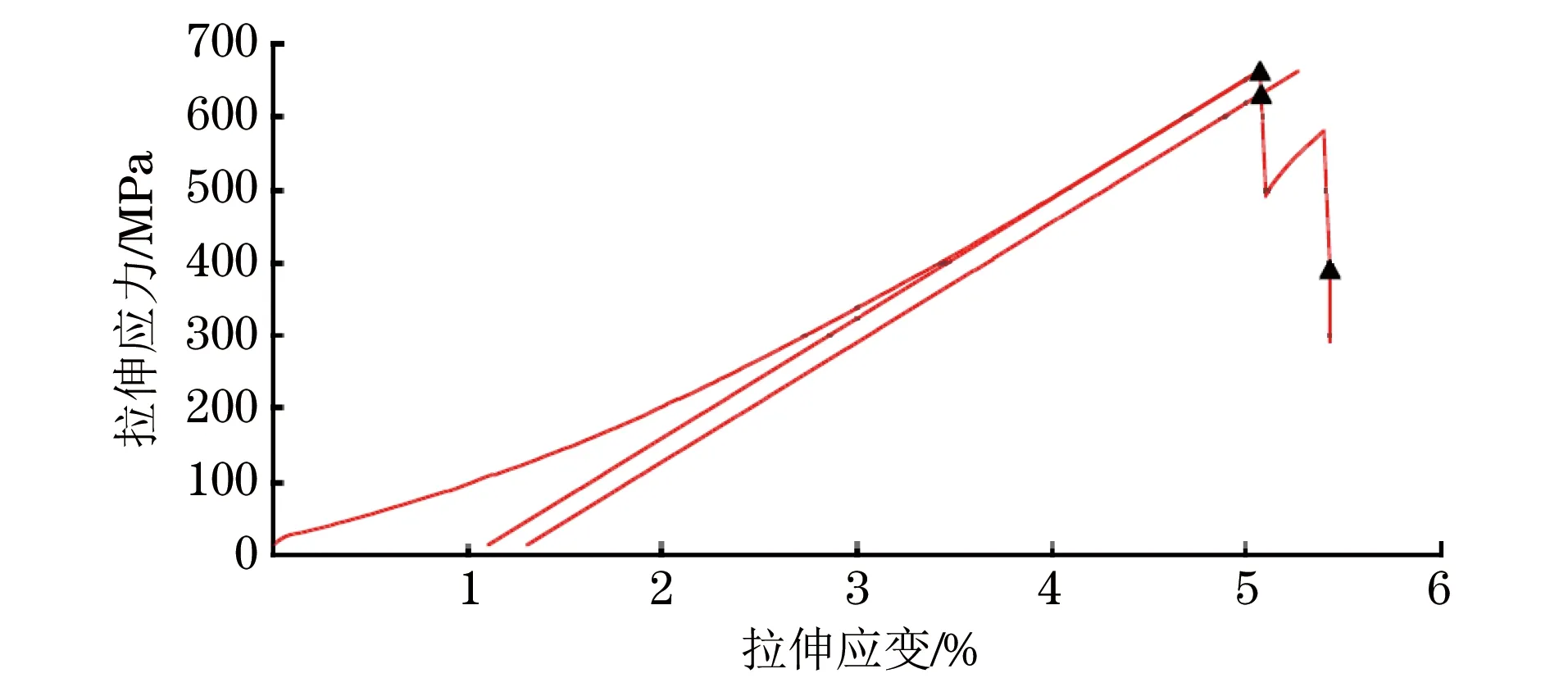
图2 拉伸应力-应变曲线
2 声发射信号聚类分析
碳纤维复合材料在拉伸过程中存在的损伤模式,主要包含基体开裂、界面层脱黏、基体断裂以及纤维断裂等4种模式,所以聚类后的数据可以分成4个簇。接下来通过K-means对数据进行聚类分析。K-means算法是一种硬聚类算法,每个聚簇都用数据集中的一个点代表,这K个聚簇被称为聚簇均值或者聚簇中心。K-means是典型的基于原型的目标函数聚类方法的代表,是以数据点到原型的某种距离作为优化的目标函数,利用函数求极值的方法得到迭代运算的调整规则。在K-means算法中,采用欧式距离作为相似度测度,最小化目标是每个点和距离其最近的聚簇之间的欧式距离的平方和最小。目标函数如式(1)所示。
(1)
式中:mx为第x个聚簇的中心;Cx为第x个聚簇;O为簇Cx中的对象。
由于声发射信号由10个属性组成,属性间的数据大小相差很大,为了使各维数据间数量级统一、加快聚类的收敛速度、降低奇异数据对算法的敏感度,需要对数据进行归一化处理。数据归一化的方法有最大最小法和平均数方差法两种,文章采用最大最小法。
图3为K值为4时,通过聚类分析后各点相对于各自聚类中心投影的轮廓值。轮廓值越接近1就表示这个点距离其聚类中心比其他中心越近,则聚类效果越好。由图3可以看出,绝大多数点的轮廓值大于0.8,所以将数据分成4类是科学有效的。

图3 K值为4时各点投影的轮廓值
由于所聚类的数据是一个多维数据,不能完整地呈现数据之间的关系,而碳纤维复合材料在拉伸过程中的损伤是随时间演化的,所以各个参数随时间的变化规律,可以揭示其内部损伤的演变规律。图4为数据聚类后幅度随时间的变化图。
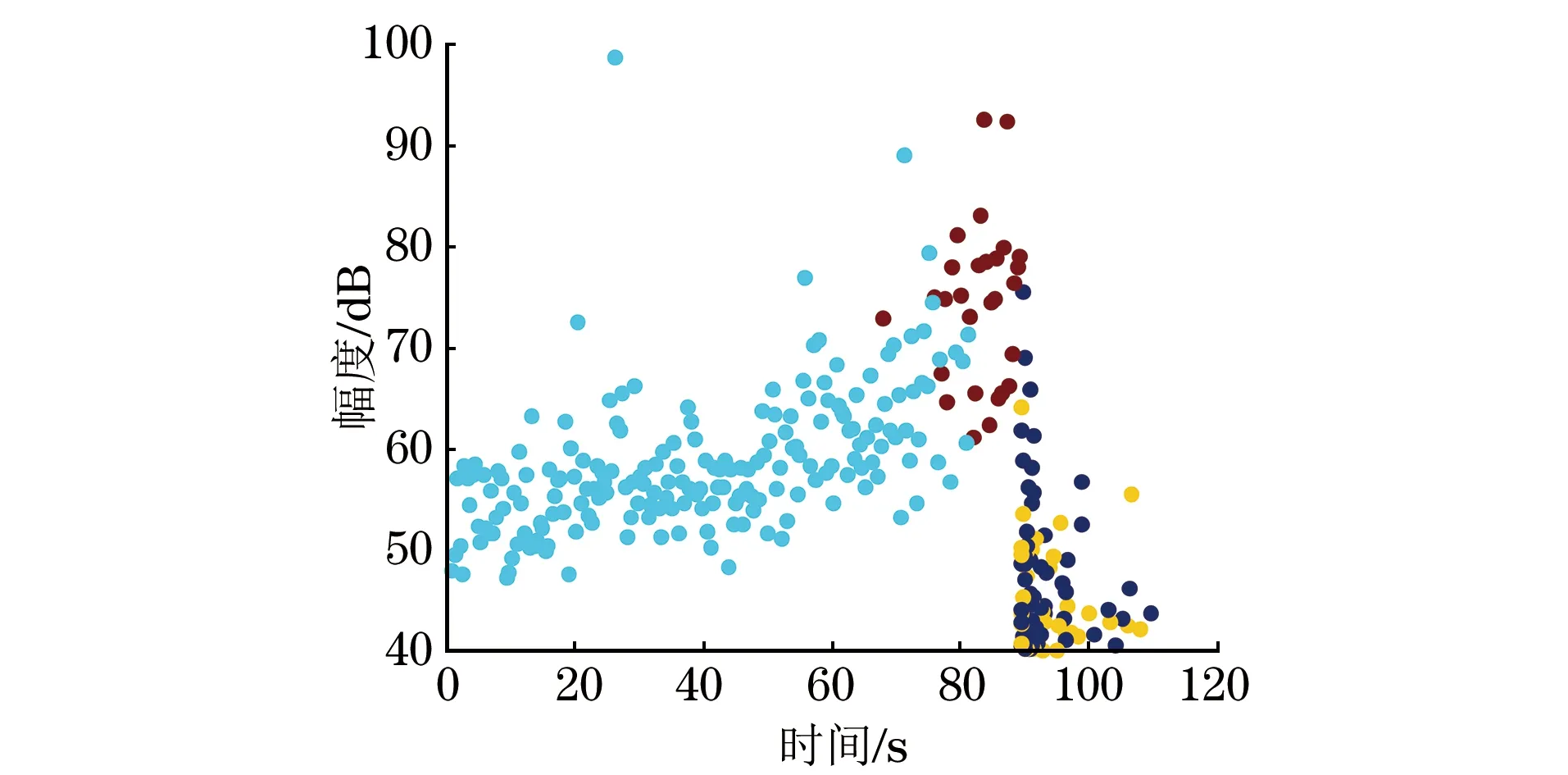
图4 幅度聚类结果随时间的变化
由图4可以看到,信号的幅度在最初的60 s内随时间缓慢增加;在60~90 s范围内随着时间的推移,幅度迅速上升,在此过程中出现了极个别幅度过大的奇异点;在90~93 s的时间段,幅度出现快速下降,幅度由最高的93 dB降为40~55 dB,直至结束。由试验可知,碳纤维复合材料在拉伸过程中首先出现基体开裂,在基体开裂末期出现了界面层脱黏,其表现形式是幅值达到极大值,接下来发生基体断裂,加在碳纤维复合板上的力由碳纤维束承担,最后出现纤维断裂。故可以看出,材料在拉伸过程中的损伤类型不是隔离的,而是在一种损伤形式发展的过程中,另一种损伤形式已慢慢出现。
3 声发射信号的模式识别
声发射信号按照损伤形式可分成4类,通过对信号进行聚类分析,可得到信号与损伤形式的对应关系。通过信号与损伤的对应关系,建立碳纤维复合板的拉伸损伤模型。将未知信号代入建立的模型,可以得到信号所对应的碳纤维复合板的损伤类型。在对对象的建模中,实际问题都存在非线性的表征,所以很难用线性模型进行描述,这就是建模的困难所在。目前,随着神经网络的出现,使得对象建模的难度大大降低,将神经网络看作黑盒子,根据输入输出的对应关系,对神经网络进行训练,最终建立相应的识别模型。为此,从323个拉伸数据中选择300个数据作为神经网络训练数据,23个数据作为识别数据,通过BP神经网络建模。由于过多的数据属性会造成训练网络的过拟合、精度降低、训练时间变长等不足,接下来采用遗传算法对神经网络算法中的参数加以优化,通过选择权值高的属性实现对数据的降维,最后比较两者的差异。
3.1 基于BP神经网络建模
要通过BP神经网络建立碳纤维复合板的声发射损伤模型,首先需要建立BP神经网络的结构。由于输入数据有10个特征参数,而通过聚类算法得到的损伤有4种类型,所以神经网络的输出为4。神经网络算法隐含层节点对BP神经网络预测精度有较大影响,节点数过少则BP神经网络学习效果变差;如果节点过多则训练时间加长,网络容易出现过拟合的状况。实际三层网络中,隐含层神经网络个数n和输入层神经元个数m有如下关系
“两线合一”即城市开发边界与生态红线的合一,其不是单纯的城市与生态空间的分界线,而是实现从增量规划到减量规划、从“多规分离”到“多规合一”的空间控制的控制线,是体现边界控制与城乡形态反映的引导线,是规划从图纸走向实施的大背景下,实现规划和管理合一的政策线,其划定过程对于积极应对城市生态环境保护与城市发展之间凸显的矛盾、加强对城乡建设的管控约束和生态安全格局的保护以及控制自然本底与城市规模的无节制扩张三个方面有重要意义。城市开发边界与生态红线划定的实质是实现空间管控,尤其是对用地规模的控制,其划定要与空间布局规划、城镇化目标、集体建设用地使用和生态空间格局进行衔接。
n=2×m+1
(2)
由于输入层有10个参数,根据式(2)确定隐含层网络节点数为21,所以BP神经网络的结构为10-21-4,即输入层有10个节点,隐含层有21个节点,输出层有4个节点。
由于BP神经网络为多输入,且各输入变量的量纲各不相同,因此在训练之前,要对数据进行归一化操作。数据归一化是指将特征值从一个大范围映射到[0,1]或者[-1,1],如果原始值都是正数,则建议选择映射到[0,1];如果原始值有正数又有负数,则建议映射到[-1,1]。由于声发射采集数据都是正数,所以需要映射到[0,1]区间。
接下来,选择BP神经网络的节点激励函数,由于隐含层和输出层函数的选择对BP网络的预测精度有较大影响。一般隐含层节点激励函数选用logsig函数或者tansig函数,输出层节点激励函数选择tansig或者purelin函数。文章选择S型正切函数tansig作为隐层神经元的激励函数。而由于网络的输出归一到[0,1]范围内,因此预测模型选取函数purelin作为输出层神经元的激励函数。
然后,设置BP神经网络的训练参数,在训练中设置网络迭代次数epochs为1 000次,期望误差goal为0.01,学习速率lr为0.01。设定完成后开始训练网络。网络训练完成后,通过测试数据对得到的BP神经网络进行测试。
图5为BP神经网络的预测输出与期望输出的比较,图6为网络误差图。由图5,6可以看到,通过BP神经网络对碳纤维复合板建立损伤模型,可以较为精确地对未知数据进行预测。测试结果为:其可以对这4类损伤进行较好识别,对第I、II、III、IV类的识别率达为100%、66%、50%、100%,但是网络的建模时间较长,达到2.886 s。
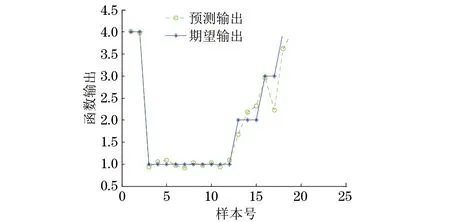
图5 BP神经网络的预测输出与期望输出

图6 BP神经网络的预测误差
3.2 基于遗传算法优化BP神经网络建模
3.1节通过BP神经网络建立的碳纤维复合板拉伸损伤模型,测试数据表明了模型的正确性。但是,由于BP神经网络的输入为10个特征参数,参数间有可能不互相独立,这样建立的模型可能会出现过拟合现象,从而导致网络识别精度变低,网络训练时间变长等。近年来学者对于自变量降维,提出了相关分析法、类逐步回归法、独立成分分析法、偏最小二乘法等方法,都取得了一定的成果。
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰适应度函数值低的解,增加适应度函数值高的解;这样进化N代后,就很有可能会进化出适应度函数值很高的个体。为此,笔者采用遗传算法对输入参数进行降维,找出权重的参数作为输入,实现对参数的降维。
利用遗传算法实现对参数的降维,首先要将解空间映射到编码空间,每一个编码对应于问题的一个染色体或者称为一个解。遗传算法首先要产生N个初始个体组成一个种群,然后以此N个个体为初始种群开始进化。一般来讲,初始群体的设定方法,一种是根据问题固有知识,设法把握最优解所占空间在整个问题空间中的分布范围,然后在此分布范围内设定初始群体;第二种方法是先随机生成一定数目的个体,然后从中挑出最好的个体加到初始群体中,通过不断迭代直到初始群体达到了预先确定的规模。由于声发射数据的属性有10个,所以将编码的长度设计为10,染色体的每一位对应于一个输入自变量,每一位的取值只能取0或者1,1表示该位置属性保留,而0则表示该位置属性舍弃。
遗传算法的第三步是进行选择操作,选择的目的是为了从当前种群中选出优良的个体,使其有机会作为父代为下一代繁殖子孙。选择操作是建立在群体中个体的适应度评估基础上的,其将优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代,进行选择时适应性强的个体为下一代贡献一个或者多个个体的概率大。
遗传算法的第四步是进行交叉、变异操作。交叉就是随机从中间群体中抽出两个个体,并按照某种交叉策略使两个个体相互交换部分染色体编码串,从而形成两个新的个体;变异即是对群体中的个体串,按照一定的概率,改变染色体上的基因值。如某个基因值由1变为0,或者由0变为1。
最终,群体经过选择、交叉、变异运算之后得到下一代群体,当满足终止条件,则进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。输出的末代种群对应的便是问题的最优解或者次优解。整个算法的流程如图7所示。
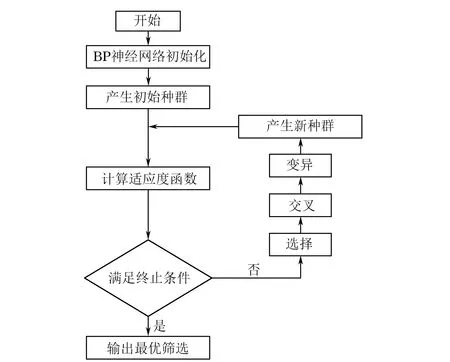
图7 遗传算法优化BP神经网络流程图
设置BP神经网络的训练参数与3.1节相同,在通过遗传算法对参数进行优化筛选时,染色体长度为10,种群大小设置为20,最大进化代数为100。利用遗传算法优化计算后,需要将筛选出来的输入自变量对应的参数提取出来,以便建立新的网络。最终,选择参数1,3,4,7,8也就是幅度、持续时间、能量、RMS和ASL作为最终的BP神经网络输入参数,显然经过遗传算法优化后,参与建模输入的参数大幅减少。
图8为遗传算法中种群适应度进化曲线,可以看出,经过5代最佳适应度已经达到0.63,当进化到11代时最佳适应度不再继续增长,输出结果已达到最优解。
最后,用测试数据对所建立的BP神经网络进行实际测试,测试结果表明:基于遗传算法优化的BP神经网络能够对碳纤维复合板的4种损伤进行识别,对第Ⅰ、Ⅱ、Ⅲ、Ⅳ类的识别率分别为100%,80%,100%,100%,并且网络建模时间大幅缩减,为0.240 6 s。

图8 种群适应度进化曲线
4 结语
通过遗传算法对神经网络的输入参数进行降维,避免了模型由于BP神经网络输入参数过多而出现过拟合、训练时间变长等问题;同时,通过遗传算法对参数进行筛选,可以筛选出权重值高的参数,为今后的研究提供了理论基础和依据。
