基于时频图像背景差分的中段多弹道目标分离*

陈 帅,冯存前,李晓华

(1 空军工程大学研究生院, 西安 710051; 2 空军工程大学防空反导学院, 西安 710051; 3 空军工程大学教务处, 西安 710051)

0 引言

弹道目标飞行中段是拦截目标的最佳时机。为了提高弹道导弹弹头的生存率,弹道导弹在飞行中段常常会释放数枚弹头以及大量干扰目标伴飞[1-2]。分离这些目标是提取目标特征的基础,国内外大量研究都着眼于弹头的微动所造成的微多普勒频率变化,碎片等干扰目标的微动形式以震动为主,弹头的微动形式主要有自旋和进动。利用微动造成的微多普勒频率变化已经成为弹头微动的重要属性。束长勇等人对锥体弹头的微动形式分别建模,利用脊线提取算法提取时频图像中的目标频率变化曲线,对曲线作频率分析来判断目标微动类型[3]。邵长宇等人将目标对应的时频曲线看作运动航迹,利用航迹追踪算法分离不同的微多普勒曲线,实现了不同散射点的分离[4]。这类方法具有创新性,但对信号本身的先验信息利用较少。

文中主要分析窄带雷达体制下的多目标分离。首先建立了双弹头滑动散射中心模型,分析了滑动散射模型中的散射点微动特性。然后建立了窄带体制下微动目标的雷达回波模型。再以时频分析为基础,对回波信号进行降噪处理后,利用重排Gabor分布对信号进行时频分析获得目标回波的时频图像。同时对目标信号利用ACF-AMDF方法估计出目标的微动周期。最后利用获得的信号微动周期结合背景差分的思想,逐个分离出各个目标的时频曲线,从而实现弹道中段多目标的分离。

1 多目标微动建模

在弹道导弹飞行的中段,弹头会绕自身对称轴自旋稳定飞行姿态。当弹头受到外力影响时会进入进动的状态,文中模型假设多目标弹头处在进动状态。建立如图1所示的多目标滑动型散射模型。其中OXYZ为雷达坐标系,假设在同一距离门内有i个弹头目标,以弹头i的质心oi为原点,目标进动轴为zi轴,zi轴与雷达视线LOSi相交形成的平面为zioiyi建立目标参考坐标系。LOSi为目标i处的雷达视线,其在雷达坐标系中的方位角与高低角为(ai,bi)。αi为弹头对称轴与zi轴的夹角,βi为雷达视线LOSi与zi轴的夹角,wi为弹头的进动速度。pij为滑动散射模型中弹头的等效散射点。j为目标上散射点的标号。

图1 弹头微动模型图

由于弹头绕着进动轴旋转,雷达电磁波入射面与弹头的相对关系变化,等效弹头底面散射点绕着底部边缘滑动,因此建立模型时只考虑一个锥底散射点。由文献[5]的结论,经平动补偿后,滑动散射模型中弹头锥顶散射中心到雷达的微距离Rpi1和锥底散射中心到雷达的微距离Rpi2可以表示为[6]:

Rpi1=Roi+hcosbicosai+hsinbisinaisin(wit-ai)

(1)

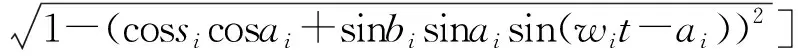
(2)

式中:Zi=Hi-hi,Hi为目标i弹头高度,hi为目标i弹头顶点到质心的距离。由式(1)和式(2)可以看出,滑动散射模型中锥顶散射中心满足正弦函数规律,锥底散射中心则相对复杂,但同样满足周期变化规律。

设雷达发射单频脉冲信号,信号工作频率为fc。单个脉冲宽度为τ,脉冲重复间隔为T。雷达发射的窄带信号可表示为:

(3)

(4)

式中:σij为散射系数,经正交双通道解调后,回波信号的形式可以表示为:

(5)

对式(5)相位项进行求导运算即可得到目标散射点的微多普勒频率:

(6)

2 滑动散射目标微动周期估计

由式(6)可知散射点的微多普勒频率和散射点的微距离相关,并且弹头锥顶散射点的微多普勒频率变化满足正弦变化规律,锥底散射点的微多普勒频率变化形式复杂,但同样是周期变化。并且同一个目标上的散射点微动频率变化周期是相同的,和该弹头的进动频率相关。对于非平稳的雷达回波信号,文中采取自相关函数法和平均幅度差函数法相结合求取目标信号周期。

设s(n)为目标回波序列,则信号的自相关函数(ACF)可以表示为:

(7)

式中:m为时间延迟量;N为信号长度。自相关函数法是利用周期信号的自相关函数也是周期信号且二者周期相同,周期信号的自相关函数在n倍周期时有极大值这两条性质求解信号周期。该方法计算量较大,遇复杂信号时,倍周期或半周期处也会出现峰值,难以准确判断周期。但该方法的抗噪声能力较强[8-9]。

同样的信号回波序列,信号的平均幅度差函数(AMDF)可以表示为:

(8)

式中:m=1,2,…,N-1。利用平均幅度差函数在n倍信号周期处有极小值这个性质可以得到信号周期,但该方法的抗噪声性能较差[8-9]。

在噪声情况下,两种方法的峰值和谷值体现不明显。利用两种方法相结合,对一段回波信号同时做自相关和平均幅度差,再将获得自相关函数与平均幅度差相比,加强信号周期处的峰值,同时减少信号倍周期和半周期处的误判。

3 时频图像背景差分

对于非平稳的微动目标回波信号,时频分析是常用的分析方法。

文中利用重排Gabor分布[10]对信号回波进行时频分析,构造时间平移和频率调制基函数gmn(t),表示为:

gmn(t)=g(t-mT)exp(j2πnFt)

(9)

式中:T、F为离散网格的单位;g为高斯窗函数。则正交解调后的回波信号Gabor分布为：

(10)

经Gabor变换后,将每个时频点处的幅值移动到该点附近的能量中心,从而得到时频信号sb(t)的重排Gabor幅值。

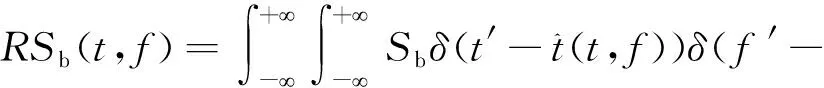
(11)

背景差分是视频处理中检测运动目标的常用方法。其原理为将各帧图像与背景图像相减,在光线环境变化不剧烈的条件下,得到像素值变化的部分就是运动目标。现实中,视频背景会随着光照变化等发生改变,这需要复杂的算法不断更新背景图像,然而掺杂噪声的目标回波时频图像处理不涉及复杂的场景变换问题,可以看作理想的运动目标检测问题[11-12]。

假设在同一距离门内有i个目标,各自对应的进动周期Ti,利用时频图背景差分分离多目标的算法流程如下:

Step 1:以第一个目标周期T1为帧长,在时频图上截取两幅图像Im1、Im2,将目标1的时频曲线看作背景,其他目标形成的时频曲线看作运动目标。

Step 2:将两幅图像相减,记S1=Im2-Im1,在两个周期内目标1的时频曲线上像素值基本相同,作为背景在第一次差分运算后被剔除。

Step 3:将相减后的图像S1像素值小于0的点置零,保存像素数据,记为M1。之后取T2为周期,重复1～3步,直到第i个目标。

Step 4:将保存的像素数据Mi-2与Mi-1相减就能得到目标i-1的时频曲线,其中Mi-1数据表示的是目标i的时频曲线,将初始时频图像定义为M0。

通过以上步骤可以看出,利用不同目标的周期将观测时间内的回波时频图像截取成不同图像。通过背景相消的方法将各个目标对应的时频曲线逐个消去,再利用记录的数据将不同目标的时频曲线恢复出来,从而完成多目标的分离。

4 仿真分析

对两个弹头进行建模仿真,弹头1和弹头2均采用滑动散射模型,远视点被遮蔽。初始时刻,弹头1质心在雷达坐标系中方位角为0 rad,高低角为0.661 4 rad。锥顶到质心的长度为1.8 m,弹头总高度为2.4 m,自旋轴与进动轴的夹角为(4/9)π rad,进动角速度为2π rad/s。弹头2质心在雷达坐标系中方位角0 rad,高低角为0.609 5 rad。锥顶到质心的长度为1.6 m,弹头总高度为2.4 m,自旋轴与进动轴的夹角为(5/18)π rad,进动角速度为3.2π rad/s。

设雷达发射频率fc=10 GHz的单频信号,脉冲重复频率为FPR=2 000 Hz,信噪比RSN=5 dB,各散射点散射系数相同。图2是回波信号的时域波形。

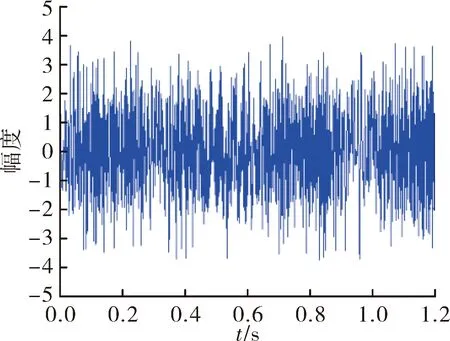
图2 回波信号时域波形

对回波信号利用小波消噪后分别求自相关和平均幅度差函数,结果如图3(a)所示,可以看到平均幅度差函数所呈现的谷值不是很明显,而自相关函数在倍频处有较高的峰值。文中将上面两种方法结合后两个目标的周期就能清晰的显现出来，如图3(b)所示。对两种方法进行抗噪声仿真,实验结果说明当RSN≤1 dB时,自相关函数法无法有效提取第二个目标的周期值,当RSN≤3 dB时,平均幅度差法已经不能分辨信号周期处的谷值,而将两种方法的结果做除法后,在RSN=-1 dB时依旧能够有效提取两个目标的周期值。

利用重排Gabor分布对回波信号进行时频分析。将观测时间设为5 s,图4为截取的1 s时间内的回波信号时频图像。运行文中提出的时频图像背景差分算法,以目标1的周期为帧长从时频图像上截取两幅图像。做差分运算后结果如图5所示,其中目标1对应的时频曲线背当作背景剔除,图像中黄色部分为目标2在第二帧中的时频曲线,被当作运动目标被保留。

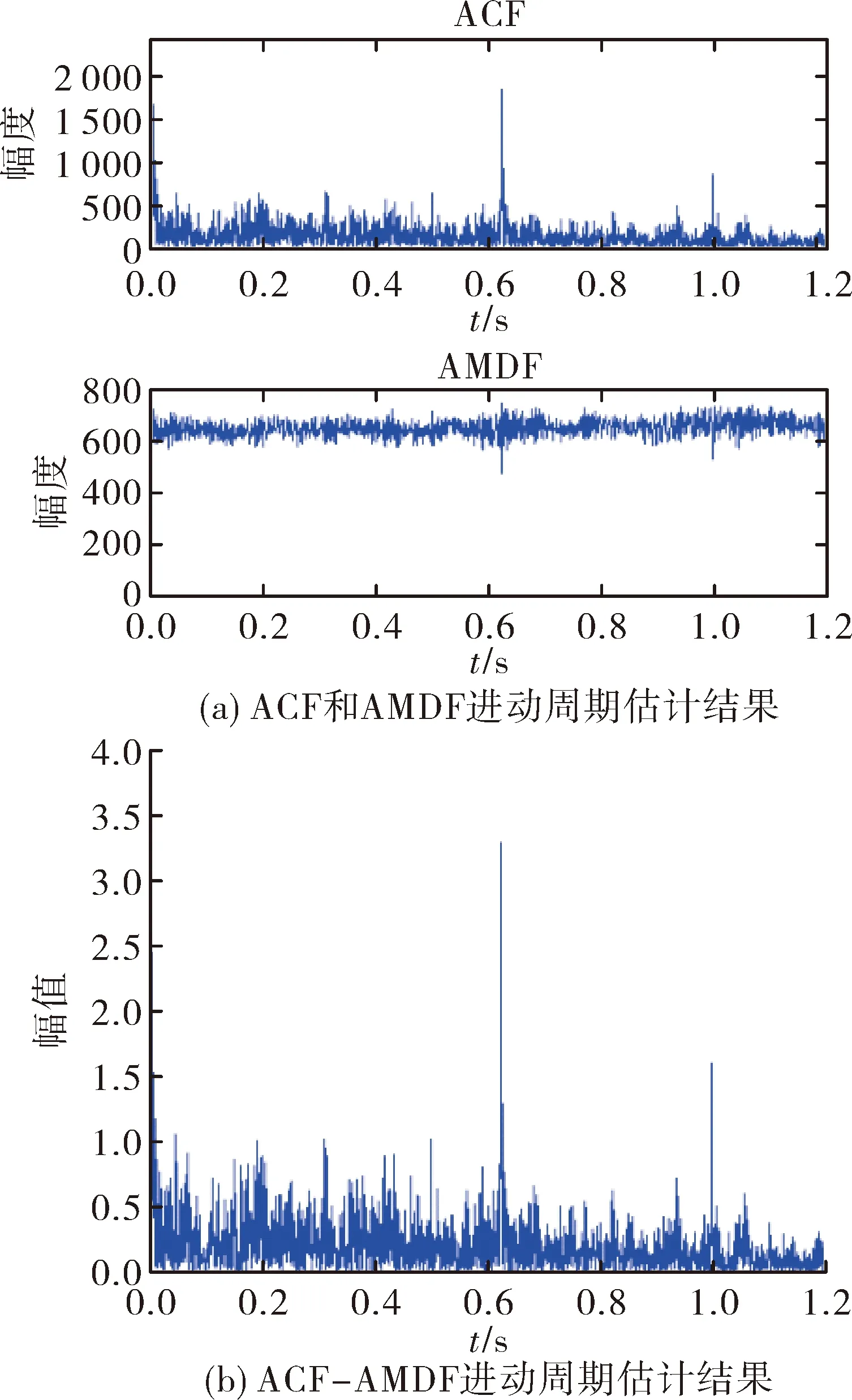
图3 微动周期估计结果

图4 回波重排Gabor时频图像

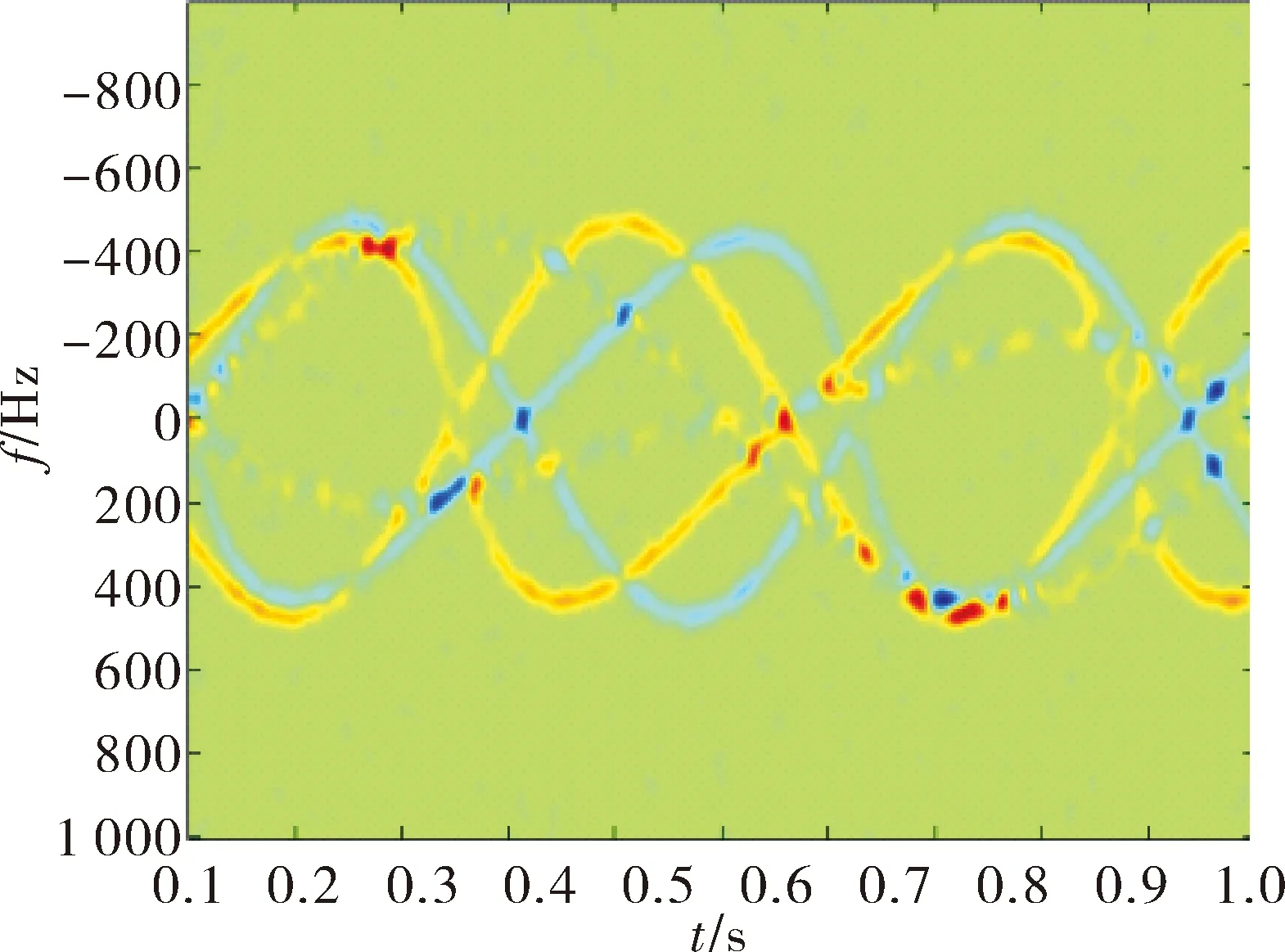
图5 背景差分后的运动部分

对图5中小于阈值的点置零,结果如图6(a)所示,即目标2的时频曲线,其中满足正弦变化规律的是目标2的锥顶散射中心,非正弦规律变化的曲线为锥底散射中的时频曲线。将获得的目标2的时频图像同上一步操作保存的数据做差分运算,得到目标1的时频变化曲线,见图6(b)。

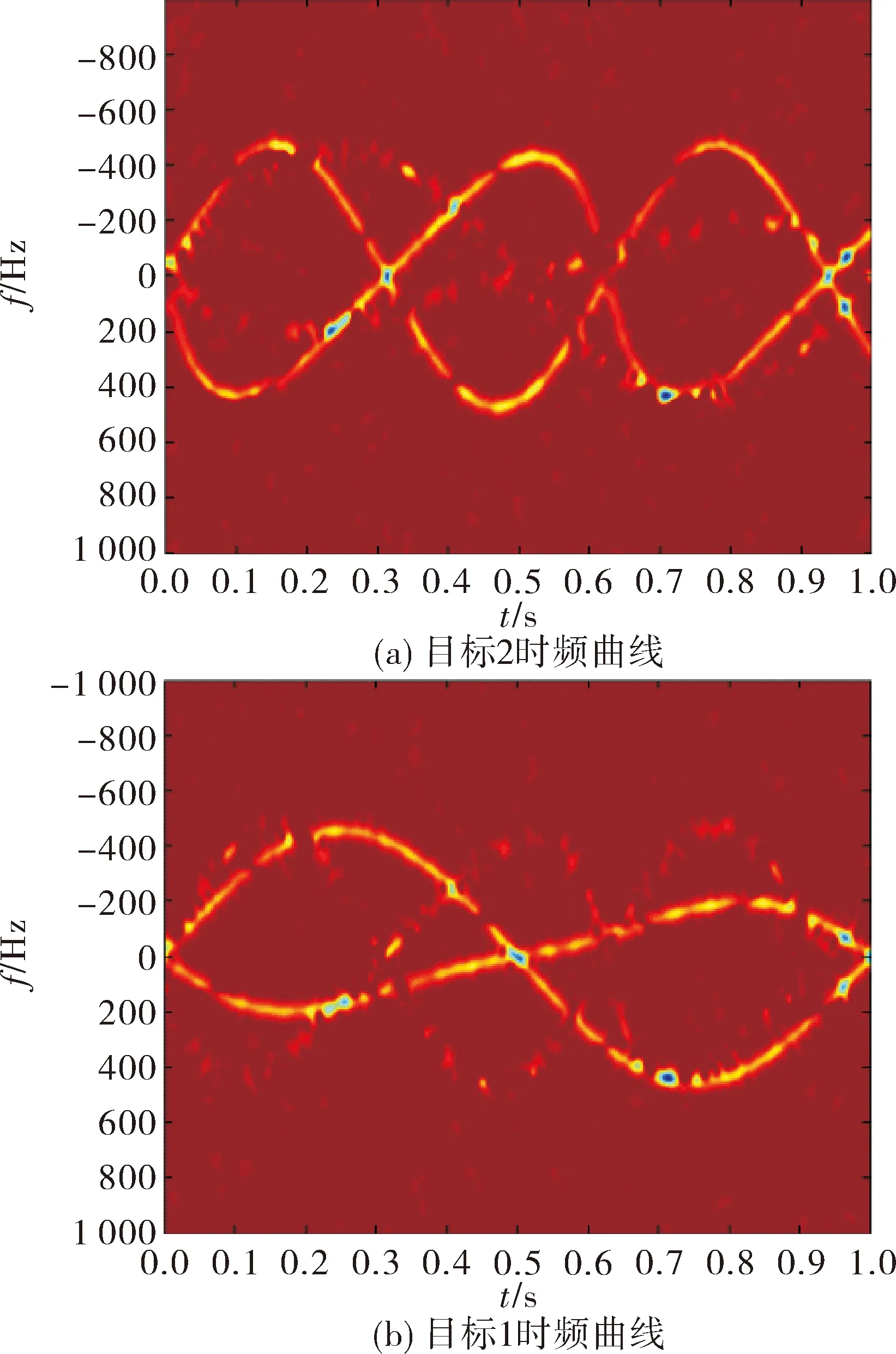
图6 弹头目标的时频曲线分离结果

通过设置阈值,对图6(a)和图6(b)的结果进行二值化处理。由各散射点时频曲线的斜率连续性可以进一步分离得到各个散射点的时频曲线,如图7所示,不同颜色的细线代表不同散射点的时频曲线。

图7 双弹头目标散射点分离结果

图8为文献[13]提出的算法分离结果,可以看到在时频图像较为复杂的情况下,不依靠先验信息获得的曲线分离效果没有文中提出的方法好。

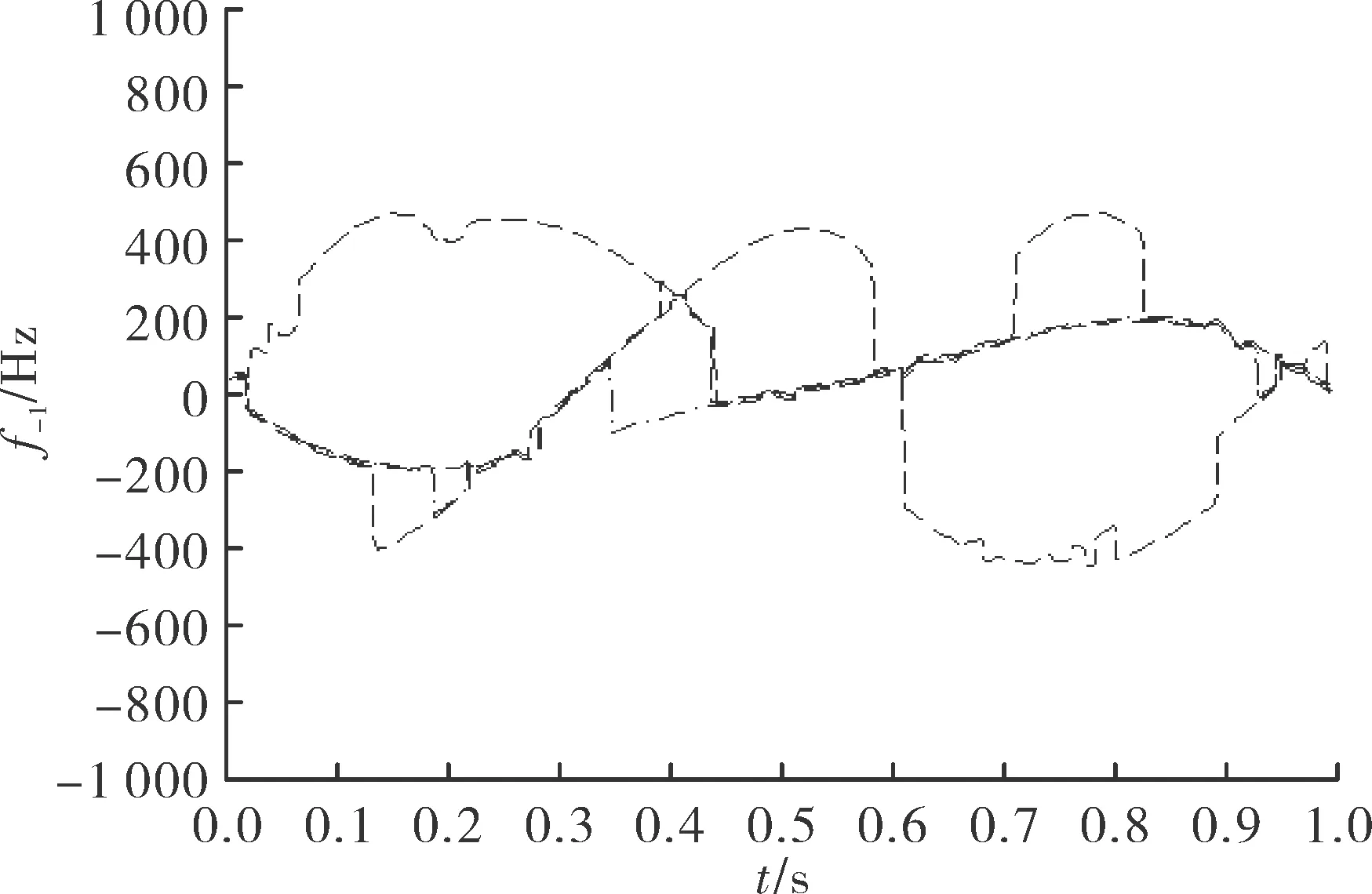
图8 文献[13]提出的Viterbi分离方法

5 总结

主要提出了基于时频图像背景差分的多目标分离方法。将目标的周期值设置为帧长,引入用于视频处理中的运动物体检测的背景差分法,将一个目标的时频曲线看作背景,先剔除运动的曲线部分,循环差分处理后最终得到全部目标的时频曲线。该方法的优势在于利用了信号的先验信息估计出了目标微动周期,利用周期和多帧图像的差分有效分离各个目标。同时也受限于周期估计的精度,需要进一步研究目标信号处理长度的最优选择,提高周期估计准确性和分离结果的有效性。