水位下降边坡的流-固耦合弹塑性分析
2019-06-22沈朝辉吴礼舟
杨 戒,沈朝辉,吴礼舟
(地质灾害防治与地质环境保护国家重点实验室,四川成都610059)
0 引 言
临水边坡在坡前水位降落时,由于水位骤降产生孔隙水滞留,坡内水位高于坡外水位,坡内外产生水压差,常发生失稳现象,如1963年的Vajont水库失事事件[1]。如何真实反映水位下降过程对临水边坡的影响是一个值得深入研究的课题。
关于水位降落对边坡稳定性影响的研究[2],目前除试验和单一渗流场理论外,较常用的研究方法是流-固耦合理论,通过考虑渗流场与应力场的相互作用来分析坡体稳定性,较符合实际。该理论需建立流-固耦合控制方程组,一般是先将有效应力原理引入平衡方程,再将体应变引入渗流连续性方程,最后将两式联立并结合几何、本构方程即得到流-固耦合控制方程组。但是,目前水位下降边坡的流-固耦合分析理论大多将土体考虑为弹性材料进行应力场分析[3-7],而土体实际上是一种弹塑性材料,也有不少学者进行了研究[8-11],但这些研究大都集中在利用强度折减法计算坡体的稳定性系数上,鲜有对坡体内部渗流、应力、位移场耦合变化的研究。
本文基于非饱和流-固耦合理论,对水位下降边坡进行研究,建立了考虑塑性变形的水位下降边坡模型,研究土体的弹塑性对渗流、应力和位移多场耦合的影响,并与弹性情况的计算结果进行比较,可为水位下降边坡的稳定性分析提供参考。
1 理论模型
1.1 基本假设
介质为均质各向同性材料;土骨架只发生微小应变;不考虑土颗粒和孔隙水的压缩,即∂n/∂t=∂εv/∂t,∂ρf/∂t=0。式中,n为孔隙率;t为时间;ρf为水的密度;εv为土骨架体积应变;饱和度Sr与有效饱和度Se相等。忽略孔隙气压力的影响,不考虑土体的硬化。
1.2 渗流场控制方程
非饱和土的连续性方程为
·ρf[-kskr
(1)
式中,Hp为压力水头;g为重力加速度;ks为饱和渗透系数;kr为相对渗透系数;y为高程;θ为体积含水率。
结合假设和VG模型[12]中的储水系数Cm对式(1)进行变形,得
·ρf[-kskr
(2)
常用的VG模型[12]关系式为
(3)
式中,θr为残余体积含水率;θs为饱和体积含水率;α、m、N为VG模型参数,其中m=1-1/N。
1.3 变形场控制方程
应用毕肖普有效应力原理[13]后的平衡方程为
-·(σ′-SepI)=[ρs(1-n)+ρfn]g
(4)
式中,ρs为土密度;σ′为有效应力张量;g为重力加速度向量;I为单位矩阵。几何方程为
ε=[(U)T+U]/2
(5)
式中,U=(u,v),u、v分别为水平位移和竖向位移;ε为土骨架应变张量。
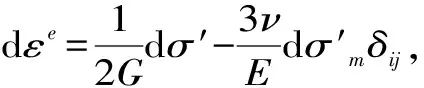
c和φ表示粘聚力和内摩擦角,θR(0≤θR≤π/3)表示罗德角[14],摩尔-库伦屈服函数为F,采用非关联流动法则,塑性势函数Q取罗德角θR=π/3时所对应的屈服函数,即Q=F(π/3),这时的Q即为π平面上不规则六边形的外接圆,收敛性良好。其关系式如下
(6)
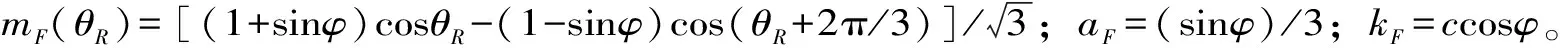
综上,式(2)、(4)为控制方程组,再结合几何方程、本构方程、初边值条件就能实现考虑塑性的非饱和流-固耦合分析。当应变增量不考虑塑性部分时,则土体简化为弹性材料。
2 数值模型及结果分析
2.1 实现方法
COMSOL是一款基于偏微分方程组(PDE)建模的多物理场耦合软件,本文通过修改固体力学和达西定律模块中内置PDE方程,实现用户自定义控制方程的输入,并利用如下函数模拟水位的下降。
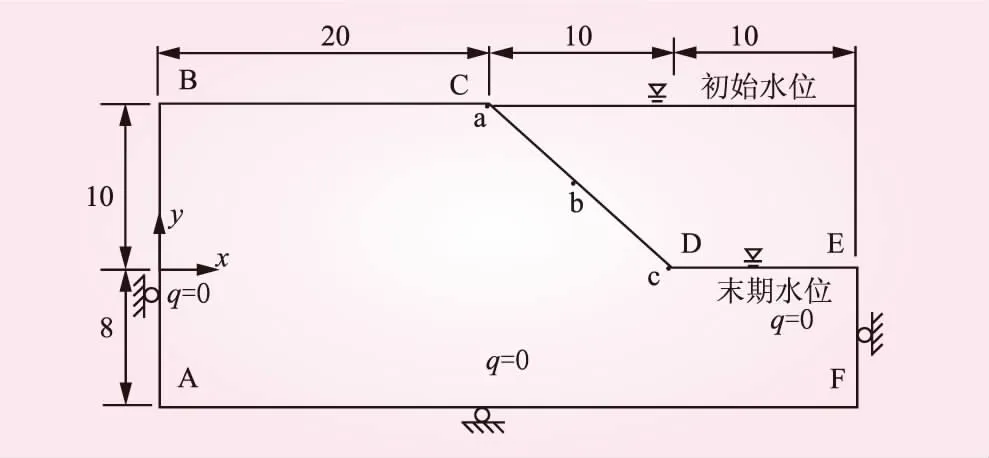
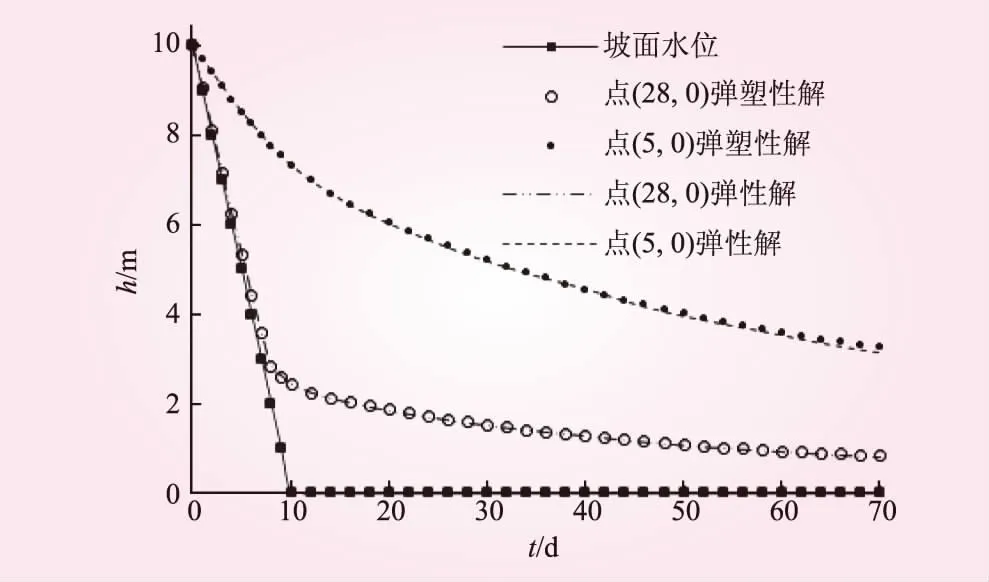
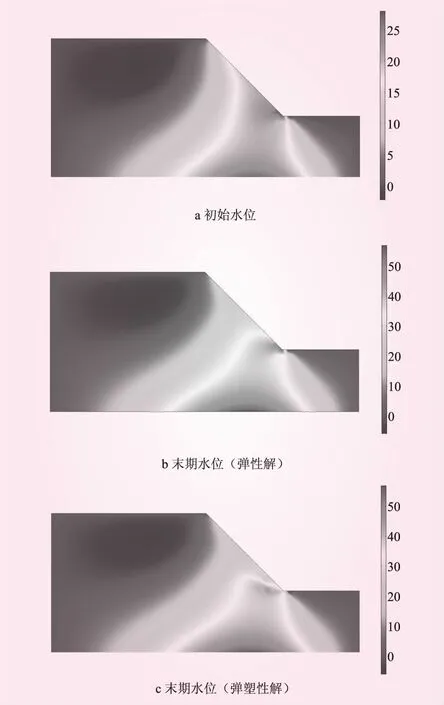
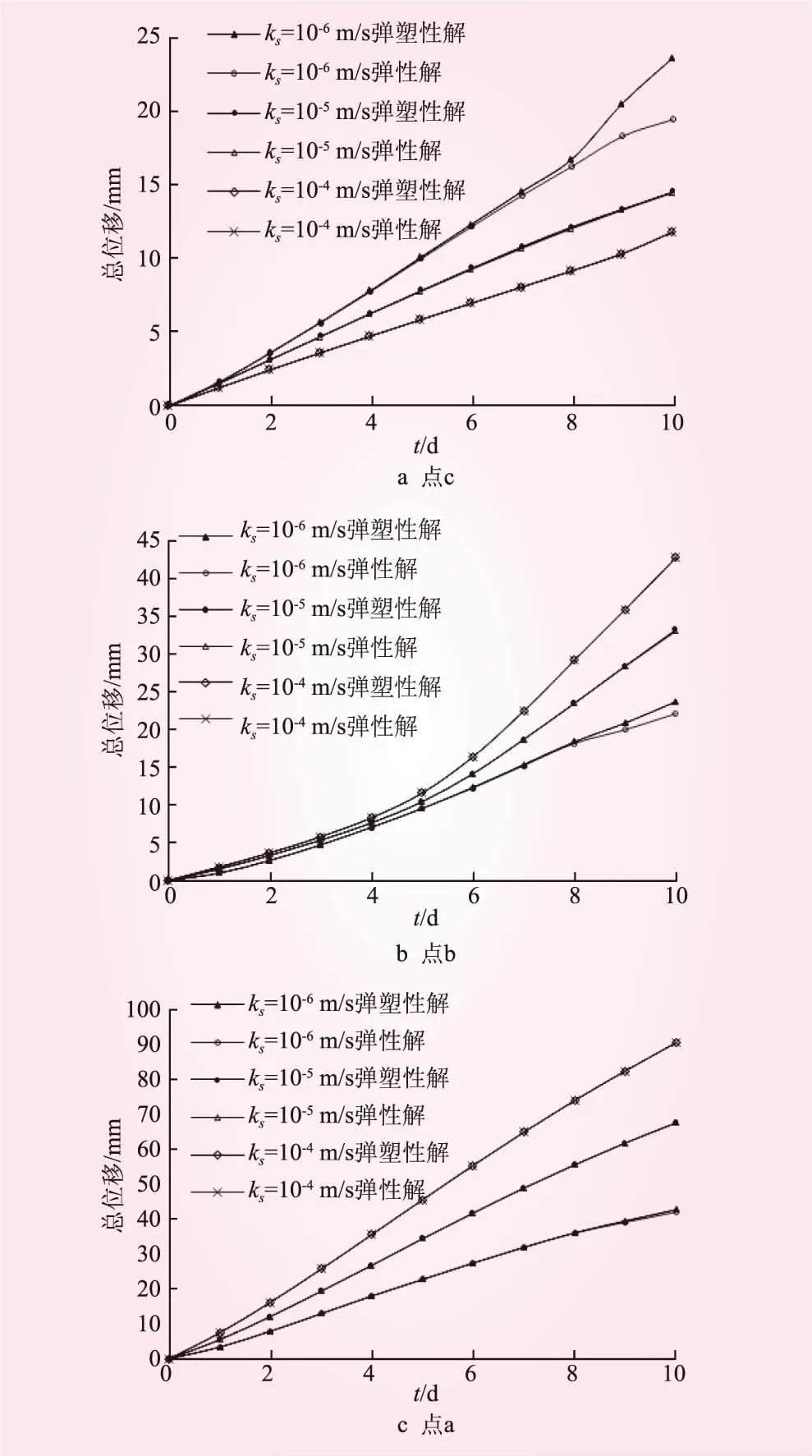
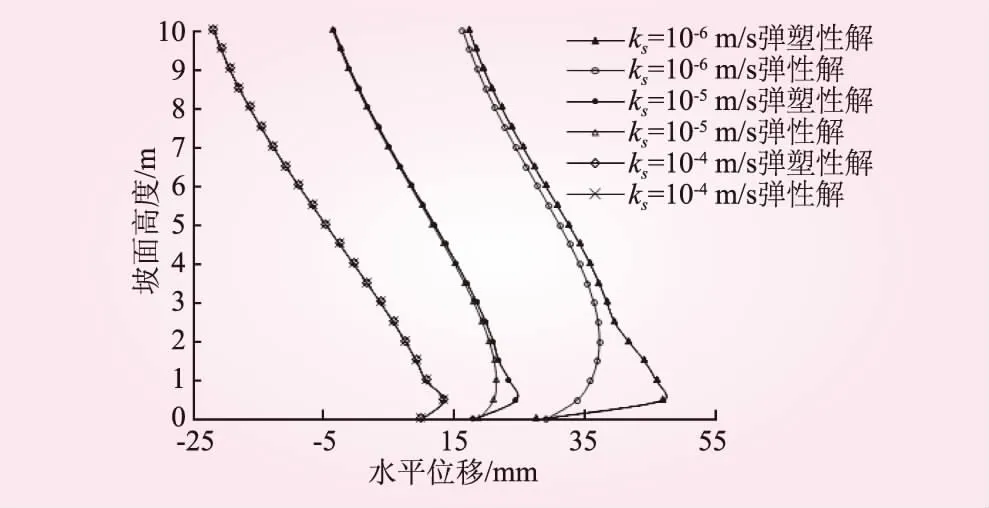
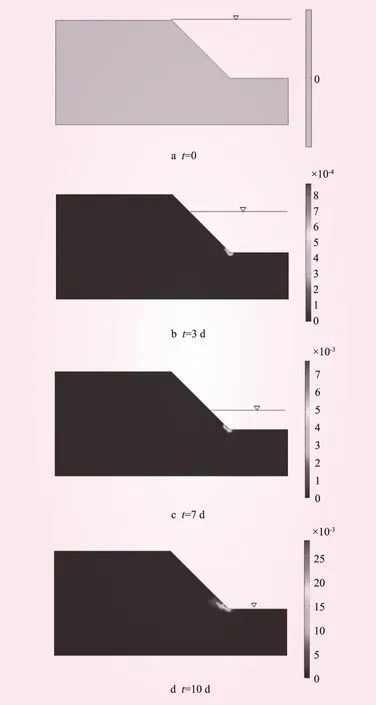
坡面变化的压力水头边界:当h0-tv0 为验证水位变化模拟的正确性,利用本文弹塑性流-固耦合的方法,对文献[15]中的水位下降边坡试验进行了计算,对压力水头随水位下降的变化情况进行了对比。边坡尺寸参考文献[15],材料为中砂(渗透系数ks=2.4×10-4m/s),试验的初始水位高度h0=0.55 m,水位下降速度v0=0.043 cm/s,坡面水位在第21 min时下降为0。以边坡剖面图的左下角为原点,图1给出了靠近坡脚和远离坡脚的2个监测点A(0.2,0.2)、B(1,0.2)的压力水头随着坡面水位下降的消散情况。从图1可以看出,计算值与试验值较为接近,说明本文的计算方法是可行的。 图1 压力水头消散对比 本文选取典型的坡度为1∶1的均质土坡算例进行分析,模型见图2。其中,AB、BC、AF、EF为不透水边界(流量q=0);CD、DE为变化的压力头和荷载边界;AB、EF限制水平位移;AF限制水平和竖向位移;a、b、c为3个特征点,分别代表坡脚、坡中、坡顶。模型参数:水密度ρf=1 000 kg/m3、土密度ρs=2 000 kg/m3、粘聚力c=25 kPa、内摩擦角φ=25°、孔隙率n=0.4、弹性模量E=10 MPa、泊松比υ=0.3、VG模型参数α=1.06 m-1、N=1.395、残余体积含水率θr=0.106、饱和体积含水率θs=0.469。 图2 边坡模型(单位:m) 2.3.1渗流场 图3给出了当ks=10-6m/s、v0=1 m/d时坡脚处点(28,0)和远离坡脚处点(5,0)压力水头h随时间t的变化情况。从图3可知,坡面水位在第10 d时下降为0;在同一高程,离坡表越近,所对应的压力水头越接近坡面水位;当水位下降至末期水位时刻,压力水头曲线有明显的转折,且观测点位置越接近坡表转折越明显;考虑弹性与考虑弹塑性得出的压力水头曲线几乎重合,故实际工程(如土石坝工程)中仅关注渗流场的变化时,可将土体简化为弹性材料计算而不会产生较大误差。 图3 压力水头消散 2.3.2应力场 图4是正应力σx在初始水位和末期水位的分布(ks=10-6m/s,v0=1 m/d)。从图4可知,初始水位时,坡脚有应力集中现象,σx值较大,坡顶后缘出现受拉;末期水位时,受拉区明显扩大,坡脚σx值明显变大,弹塑性解的坡脚应力集中现象还有向深部发展的趋势,而弹性材料无这一现象,但弹性解与弹塑性解的差异在坡脚以外的区域并不明显。图5是剪应力τxy在初始水位和末期水位的分布(ks=10-6m/s,v0=1 m/d)。从图5可知,初始水位时,坡脚同样也有应力集中现象,τxy值较大;末期水位时,坡脚τxy明显变大,弹塑性解坡脚应力集中现象也有向深部发展的趋势,若土体强度不足,则可能向深部发展甚至贯通整个坡体形成滑面,而弹性解无法反映这种情况。 图4 正应力 σx分布(单位:kPa) 图5 剪应力τxy分布(单位:kPa) 2.3.3位移场 图6给出了v0=1 m/d时,3个特征点a、b、c坡面总位移随时间t的变化情况。从图6可知,当ks=10-4m/s时,弹性解与弹塑性解在点a、b、c都没有差异;当ks=10-5m/s时,弹性解与弹塑性解在点a、b、c有微小差异;当ks=10-6m/s时,弹性解与弹塑性解在点a、b、c出现差异,且差异从a点至c点逐渐增大。因此,当水位下降速度一定时,总位移的弹性解与弹塑性解的差异与特征点位置和饱和渗透系数有关:ks越小,弹性解与弹塑性解的差异越大,尤其在坡脚。 图6 总位移变化 图7为水位下降末期的坡面水平位移分布。从图7可知,ks=10-4m/s时,弹性解与弹塑性解无差异;ks=10-5m/s时,弹性解与弹塑性解出现差异,且在坡脚尤为显著,弹塑性解在坡脚处出现了尖点,而弹性解没有出现尖点;ks=10-6m/s时,弹性解与弹塑性解的差异又进一步扩大。因此,ks越小,弹性解与弹塑性解的差异越大,尤其在坡脚,结论与图6相似。 图7 末期水位坡面水平位移 图8 点c的总位移 图9 等效塑性应变 由于坡脚应力集中较为明显,且上述分析中考虑弹塑性对坡脚的影响比其他区域大,因此继续对坡脚进行分析,图8给出了坡脚c点(ks=10-6m/s)在不同水位下降速度v0的总位移变化。从图8可知,较大的v0会产生较大的总位移;随着水位的逐渐下降,c点弹性解与弹塑性解的差异也逐渐变大(v0越大差异越明显);当v0=0.1 m/d时,弹性解与弹塑性解的差异基本消失;v0=0.5 m/d时,弹性解与弹塑性解在水位下降7 m时出现差异,且随着水位的下降,差异逐渐变大;v0=1 m/d时,弹性解与弹塑性解在水位下降6 m时出现差异,且在相同水位高度v0=1 m/d时的差异比v0=0.5 m/d时大。因此,当ks为定值时,v0越大,弹性解与弹塑性解的差异就越大。 边坡破坏可看作是塑性区逐渐发展、扩大直至贯通而进入完全塑流状态、无法继续承受荷载的过程。图9给出了边坡塑性区的动态发展过程(ks=10-6m/s、v0=1 m/d)。由图9可知,t=0时,坡内还未产生塑性区,整个坡体处于稳定状态;随着水位的下降,塑性区首先在坡脚出现并逐渐向深部发展,由于岩土体具有一定强度,塑性区发展未贯通,边坡仍处于稳定状态;若岩土体强度不足,则塑性区将由坡脚向坡体深部贯通,从而影响边坡的稳定性;塑性区主要集中在坡脚,这也可解释为何将土体分别考虑为弹性和弹塑性材料时,在坡脚体现的差异最大;而随着水位下降,塑性区逐渐扩大,从而也将导致弹性和弹塑性材料之间的偏差逐渐增大。 本文基于非饱和土流-固耦合理论,对水位下降的边坡进行了研究,得出以下结论: (1)实际工程(如土石坝工程)中仅关注渗流场的变化时,可将土体简化为弹性材料计算而不产生较大误差。 (2)弹塑解对应力场的影响主要在坡脚,弹塑性解能反映水位下降时坡脚应力集中向深部发展的现象,而弹性解无法反映这种情况。 (3)弹塑解对临水边坡位移场的影响与土体饱和渗透系数和水位下降速度有关。水位下降速度为定值时,饱和渗透系数越小,弹性解与弹塑性解的差异越大,尤其在坡脚;饱和渗透系数为定值时,水位下降速度越大,弹性与弹塑性之间的差异越大。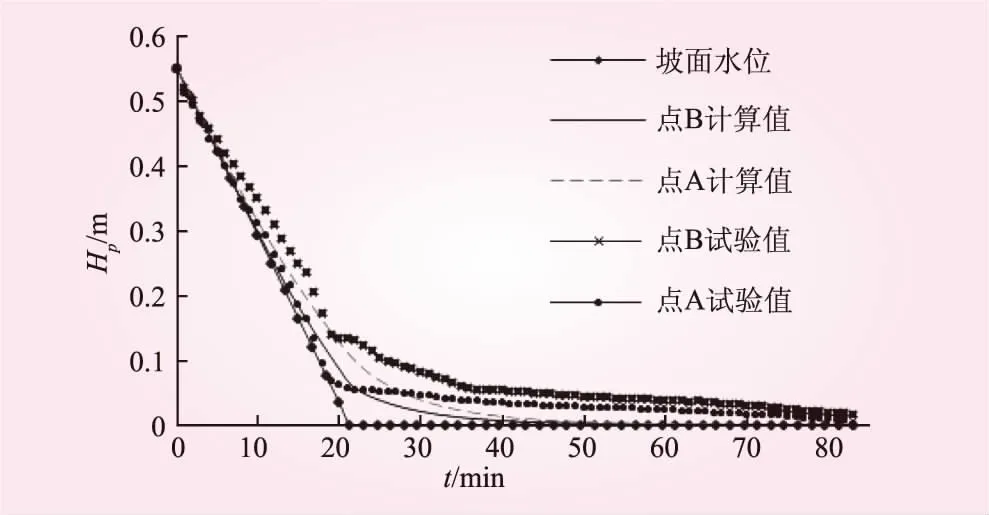
2.2 模型简介
2.3 计算结果分析


3 结 语
