熵权法并联组合模型在大坝变形监测中的应用

郑旭东，陈天伟，邓捷利，段青达，甘 若，王 雷

(1.桂林理工大学测绘地理信息学院，广西桂林541004；2.广西空间信息与测绘重点实验室，广西桂林541004)

0 引 言

目前，大坝变形预测的方法主要有BP神经网络法、支持向量机法、相关向量机法、时间序列法等[1]。由于大坝工程的复杂性，以及外界条件的不确定性，决定了使用单一预测模型进行变形预测时，难以得到预测精度和预测期数都较为优秀的预测结果。针对大坝变形预测中存在的种种问题，部分学者进行了如下研究：王利等使用改进灰色模型在大坝沉降预测中取得相对误差小于2%的预测结果[2]；何启等使用改进的加权马尔可夫链模型得到了平均相对误差为0.71%的预测结果[3]；覃邵峰使用改进的ARIMA模型在大坝变形预测中平均相对误差为0.48%[4]。为了能在实际预测中尽可能地发挥单一模型的预测优势，又能约束各自的缺陷，本文基于信息熵原理提出熵权法并联组合模型。使用灰色—加权马尔可夫链预测模型用于解决变形预测中“少数据，贫信息”以及灰色模型预测周期短的问题，同时使用ARIMA模型来提高预测结果的精度，利用最大熵原理对两模型合理组合，得到一个精度更高、更加合理的预测模型。

1 模型介绍

1.1 灰色—加权马尔可夫链

1.1.1灰色预测模型GM(1.1)

灰色理论主要研究“小样本，贫信息”的不确定系统的问题[5]。建立灰色模型时，为了淡化原始数据随机性误差的影响，首先对原始数据进行累加处理，再用微分方程进行建模，最后对模型值进行还原，得到预测值。由于该模型在其他文献中出现较多，本文不再加以详述。

1.1.2加权马尔可夫链预测

对于一组随机变量，在验证其满足“马氏性”后，通过各步长的状态转移矩阵，以及其相对应的状态做出预测后，利用其各阶自相关系数能够描述出各种滞时指标值相关关系的强弱这一特性[6]，对各步长的预测结果按照相依关系的强弱进行加权平均，这就是加权马尔可夫链预测法的基本思想。

加权马尔可夫链预测的步骤：

(2)“马氏性”检验。

(3)计算各阶自相关系数rk，k∈E

(1)

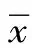
(2)

式中，wk为各个滞时(即步长)的马尔可夫链的权重；m为预测的最大阶数。

(4)根据步骤(1)所划分的状态，统计出各步长的状态转移概率矩阵。

(6)将同一状态的各预测概率加权求和作为该指标值处于该状态的预测概率，即

(3)

则最终该指标值的预测状态，即max{Pi，i∈E}。

(7)求出级别特征值对预测值进行估算[7]。待该指标值预测完成后，将预测值加入到原始序列中，重复步骤(1)～(7)即可完成对下一指标值的滚动预测。

1.1.3灰色—加权马尔可夫链

灰色预测模型的优点是需要的数据信息较少，但其预测时间较短，而且对于波动性较大的数据，预测效果也不尽人意。而马尔可夫链预测模型是通过统计原始序列得到状态转移概率矩阵进行预测，能够在对变化较大的随机序列的预测中取得不错的效果，但其需要足够多的原始数据来统计出原始序列的内在规律。故将两模型进行串联组合，用马尔可夫链预测模型对灰色模型的结果进行改正，以提高预测精度。其具体步骤如下：

(1)将灰色模型的拟合值和实际观测值进行对比，求出相对误差。

(2)用求出的相对误差进行马尔可夫链建模，由马尔可夫链预测模型预测出某时段的相对误差。

(3)用马尔可夫链预测模型预测出的相对误差对灰色模型的预测值进行改正。

1.2 ARIMA模型

ARIMA模型也写作为ARIMA(p，d，q)模型，它的实质是将ARIMA(p，q)进行d阶差分得到的。通过这样的操作，把一个非平稳的时间序列转化成一个平稳的时间序列，再通过观察相关函数结尾和拖尾特征得到自回归阶数p和移动平均阶数q，对时间序列进行ARIMA建模，达到预测的效果[8]。ARIMA模型为

φ(B)(1-B)dYt=θ(B)et或
φ(B)dYt=θ(B)et

(4)

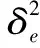
1.3 基于熵权法的组合模型

并联组合模型的关键在于对单一模型的确定及单一模型权重的确定。本文采用熵权法确定各个单一模型权重，建立组合模型来预测大坝变形的数据。熵权法是根据评价对象的指标值构成的判断矩阵来确定权重的一种方法。如果把信息熵理解为某种特定信息xi出现的概率p(xi)，那么信息熵H(x)的定义为

(5)

根据信息熵的定义可知，我们将特定信息认为是单项预测模型的误差，如果单项模型的误差的信息熵越小，其变异程度也就越大，则该单项预测模型的权重也越小。反之，模型误差的信息越大，那么其变异程度越小，则模型的权重也就越大[9]。

因此，可以利用信息熵原理来确定单一模型的权重。具体步骤如下：

(1)计算单个模型对应时刻的相对误差权重

(6)

式中，eij为第i个模型第j时刻的相对误差。

(2)计算第i个模型相对误差的熵值

(7)

式中，k=1/lnn，其中，n为选择的单一模型数量。

(3)计算第i个模型相对误差序列的变异程度系数

di=1-Hi

(8)

(4)计算第i个模型的权重系数

(9)

(5)将单一模型的预测值和求得的权重加权求和，获得组合模型的预测值

(10)

式中，yi为单一模型的预测值。

组合预测模型建模基本流程如图1所示。

图1 组合模型建模流程

表1 各模型预测值对比

2 具体实例

本文以某大坝水平变形监测点水平径向位移观测值为例，数据来源于文献[2，10]。这里取前16期的观测值作为原始起算数据，后4期数据和预测数据进行对比。观测原始数据如图2所示。

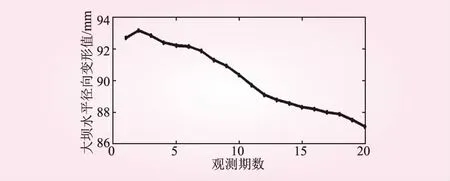
图2 原始数据

2.1 单项模型预测

将灰色模型预测得到的前16期的拟合值与实际观测值对比得到的相对误差，对相对误差进行马氏性检验，用马尔可夫链模型进行建模，预测得到后4期相对误差，用此结果对灰色模型的预测值进行改进，即可得到灰色—加权马尔可夫链预测模型的预测值；将前16期数据进行一阶差分处理，对处理的数据进行自回归系数与偏回归系数分析，确定ARIMA(p，d，q)模型的参数。经分析，确定p=3，d=1，q=3。利用SPSS软件进行ARIMA建模，获得预测值。其结果见表1。

2.2 单项模型熵权计算

根据前文介绍的熵权计算公式以及两个单一模型的变形值的预测结果，可得到灰色—加权马尔可夫链预测模型，ARIMA预测模型在并联组合模型中所占的权重分别为：ω1=0.75，ω2=0.25；再由式(10)求得最终大坝水平径向位移的预测值Y={87.837，87.555，87.196，86.862}。

2.3 结果分析

为了更加直观的表现出3种模型的预测效果，把3种模型的预测结果与实测值的对比用折线图的形式表现，如图3所示。

表中，模型一是指灰色—加权马尔可夫链模型，模型二是指ARIMA模型，模型三是指基于熵权法的组合模型。

从表1、图3分析相对误差可得，组合模型预测效果最好，平均相对误差约为-0.26%，其次为ARIMA预测模型，平均相对误差约为0.27%；加权马尔可夫链预测模型相对较差，平均相对误差为0.46%。单就平均误差而言，组合模型和ARIMA模型差别不大。为了进一步分析3种模型的平稳性以及精确度，按照整体评价预测方法的原则，引入以下评价

(10)

表3 预测结果对比

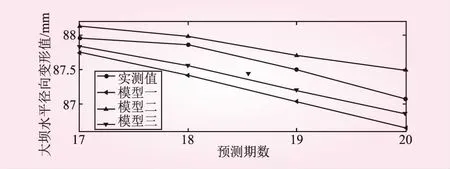
图3 各模型预测值与真实值对比

(11)

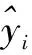
根据以上两种评价指标，得出预测评价结果见表2。

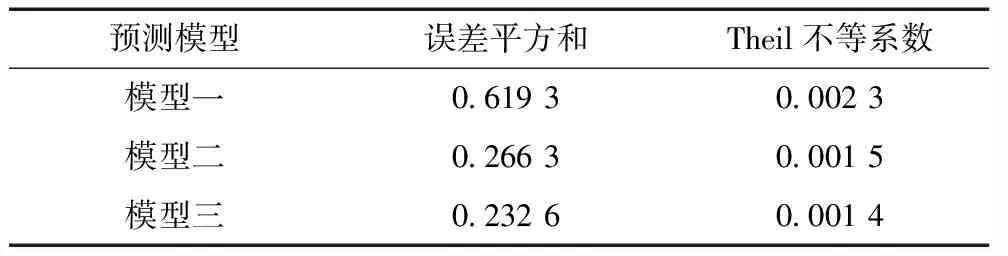
表2 模型的评价指标对比

实例分析表明，组合模型的预测精度最好，与实际观测数据相比较，Theil不等系数和误差平方和均优于单一的预测模型，显示出它在大坝变形预测精度上的优越性；其次，组合预测模型可以有效的弥补单一预测模型实际预测中存在的不足。对于现有的大坝变形预测模型而言，并联加权模型可以合理的结合各单一模型的优点，提高预测结果精度。为避免其偶然性，笔者使用文献[3]中的数据再次进行实验，求得的模型一和模型二的权重为ω1=0.14，ω2=0.86。由于篇幅限制，在此只对结果进行呈现。其结果见表3、4。

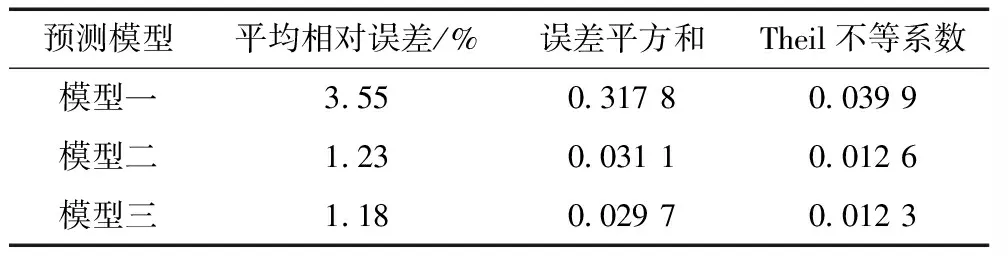
表4 预测结果精度指标对比

由表3、4结果可知，对文献中的大坝水平位移分别进行灰色—加权马尔可夫链模型，ARIMA模型和组合模型的预测，得到的预测结果从平均相对误差，误差平方和，以及Theil不等系数来看组合模型均为最优，由此可见基于熵权法的并联组合模型对于大坝变形预测来说是一种行之有效的预测方法。

3 结 论

本文针对有限的观测数据，结合灰色理论适用于“小样本、贫信息”的特点；马尔可夫链能够准确拟合波动性较大的数据的特点；ARIMA模型能够挖掘非平稳时间序列的内部信息，拟合出变化趋势，从而实现预测目的，具有建模简单的特点；并且结合最大熵的原理对模型进行合理的组合，建立了基于最大熵原理的混合预测模型，通过实例验证了该模型对于小样本序列预测精度较高。具体结论如下：

(1)基于信息熵原理，建立并联组合模型来预测大坝的形变量，该方法在精度上较单一模型有所提高，并且平衡了单一模型的实测数据和样本数据之间在质量和数量上的需求，同时能够平衡各单一模型的拟合及预测精度以及普适性等方面的优点及缺点。

(2)基于信息熵原理，可对在真实值上下浮动的单一模型的预测值进行合理组合，减少了人为因素，使得组合模型在预测结果上更加接近真实值，从而提高了预测模型的预测精度以及合理性，为数据处理以及大坝变形预测提供了一条新的途经。