基于M AT L A B的P I D参数整定的仿真与分析

2019-06-22赵文豪张晨宇张国欣

装备制造技术 2019年3期

张震，赵文豪，张晨宇，张国欣

（武汉工程大学，电气信息学院，湖北武汉430200）

0 引言

PID控制器结构简单，在诸多领域都得到广泛的应用，但是，一方面，当被控对象变得复杂时，传统的PID控制器在面对时变系统和非线性系统很难取得较好的控制效果[1]。神经网络控制可以克服以上问题。另一方面[2]，采用常规PID控制器虽然简单易行，但一组固定不变的PID参数无法适应参数变化，难以获得满意的控制效果。甚至当参数变化范围太大时，系统性能会明显变差。基于神经网络的优点，把PID控制和与其结合起来，构成BP神经网络PID控制，能够实现较好的控制效果。

1 基于BP神经网络的P I D控制器的设计

1.1 BP神经网络控制器原理

BP神经网络的优点在于他可以逼近任意的非线性函数，而且不需要太复杂的结构就可以拟合复杂曲线，它已经有了较为成熟的算法，可以通过BP神经网络的算法拟合P、I、D三个参数之间的非线性关系。基于BP神经网络的PID控制系统结构如图1所示。

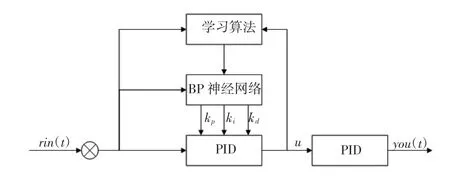
图1 BP神经网络P I D控制结构图

在增量式数字PID的控制算式将kp、ki、kd作为系统运行状态的可调系数时，可得

假设BP神经网络结构如图2所示，有4个输入神经元，5个隐含神经元，3个输出神经元。输出分别对应PID控制器的三个参数kp、ki、kd，输出层神经元的激活函数取非负的函数。

图2 BP神经网络的结构图

网络输入层的输入为：

网络隐含层的输入，输出为

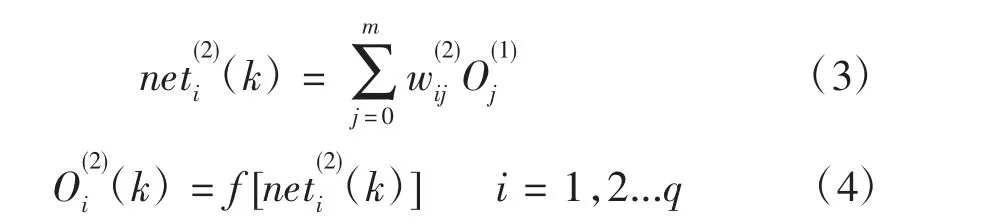
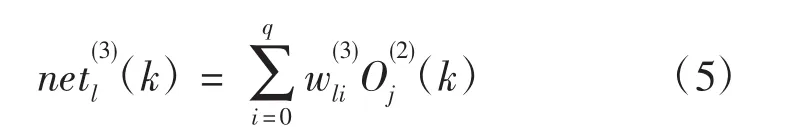
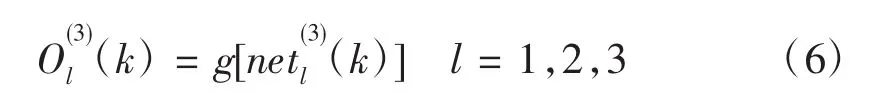
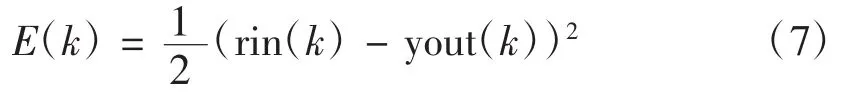
本研究中使用的是最速梯度法调整各层权值，并附加一使搜索快速收敛全局极小的惯性项[2]。

本研究中，BP神经网络的结构为图2，分为三层：输入层、隐含层、输出层。输入层有4个神经元，隐含层有5个神经元，输出层有3个神经元。习速率为 0.1，惯性系数为0.01，各层之间的初始权值取［-0.5，0.5］上的随机数，输入变量为：给定期望输出量 rin（t）、实际输出量 you（k）、偏差 e（k）及常数 1。输出变量为：PID 三个可调参数 kp、ki、kd[4]。

1.2 BP网络的P I D控制器算法

1）确定神经网络输入层节点及数目、隐含层数目、各层权系数的初值、学习率、惯性系数；

2）采样得到 rin（t）、you（t），计算该时刻误差；

3）计算神经网络各层神经元的输入、输出

4）计算PID控制器的输出；

5进行神经网络学习，在线调整加权系数；实现PID控制参数的自适应调整；

2 基于模糊P I D的控制器的原理及设计

模糊控制的优点在于它有较好的自适应能力，对非线性的系统和含大滞的系统有较好的控制效果。而自适应模糊PID控制就是根据实际情况实时调整比例、积分、微分系数，以达到控制作用在任何时候均为最优[3]。其结构如图3所示。

图3 模糊P I D控制系统结构

在图 3 中，rin（t）表示输入信号、you（t）表示输出信号，e、表示误差 ec 表示误差变化率。kp、ki、kd是模糊PID控制器的三个控制输出，这三个控制输出作为常规PID控制器的比例系数、积分系数和微分系数。PID的参数模糊自整定的实质就是找出控制器中PID的3个参数与e和ec之间的实际存在的非线性关系，然后根据事先设定好的模糊控制的规则来实时修改这个三个输出参数并输出，这样就可以满足不同e和ec所需要的不同控制参数，从而达到控制效果[2]。

本次研究中用到的偏差e、偏差的变化率ec所对应隶属度函数用的就是三角隶属度函数，而且输出参数kp、ki、kd也都是三角隶属度函数，在这里设置的模糊论域也都是一样的{-3，-2，-1，0，1，2，3}，与之相对应的模糊子集是{NB，NM，NS，0，PS，PM，PB｝，模糊子集中的元素代表｛负大，负中，负小，零，正小，正中，正大｝。现在已知条件下设 e，ec 和 kp、ki、kd都服从一般的正态分布，则可以得出各模糊子集所对应的隶属度，然后根据每个模糊子集隶属度的赋值表和每个参数模糊控制的模型，通过模糊合成再推理设计出PID三个输出参数的三个模糊矩阵表，最后进行计算得到三个控制的输出参数。主要过程是对模糊逻辑规则产生的结果进行处理、查表和运算，然后再完成对PID三个参数的在线自动的校正[4-5]。

3 模糊P I D控制器的算法流程

（1）获取当前采样值；

（2）计算误差得 e（k）Ec（k）；

（3）对 e（k）、Ec（k）模糊化；

（4）模糊整定△kp、△ki、△kd；

（5）计算PID控制器输出。

4 仿真结果及分析

为了对比常规PID、BP神经网络和模糊PID的控制效果，这里是基于MATLAB平台来进行的仿真验证，传递函数模型为[6-10]：

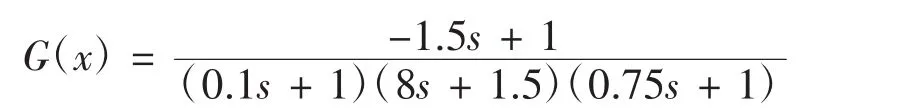
此传递函数是从水轮机的实际模型抽象出来的，此模型为三阶含非最小相位系统，比较难控制。原系统的阶跃响应如图4所示。

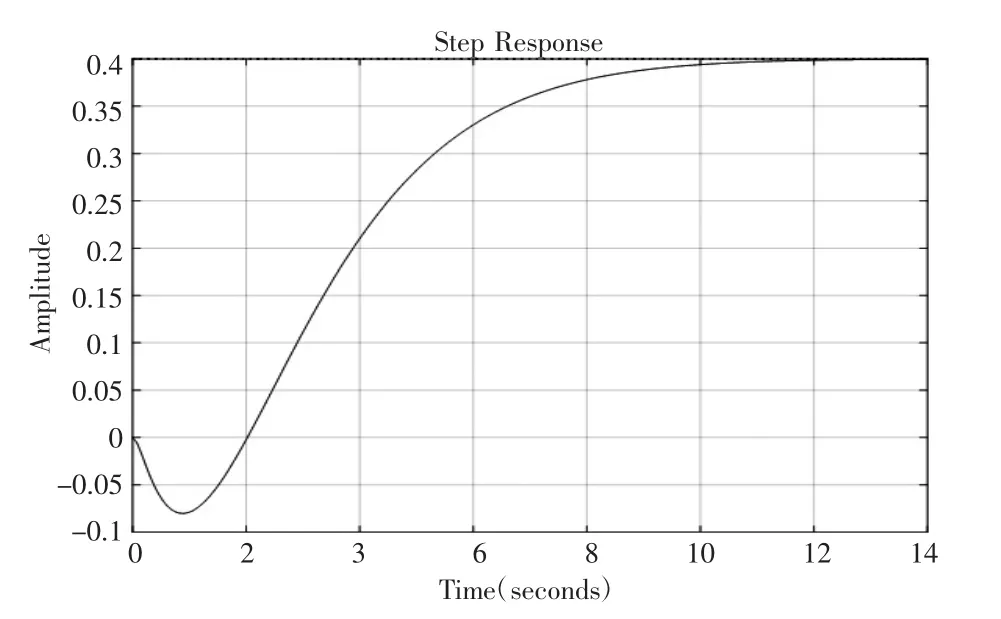
图4 原系统阶跃响应

常规PID控制和模糊PID控制仿真效果如图5所示。

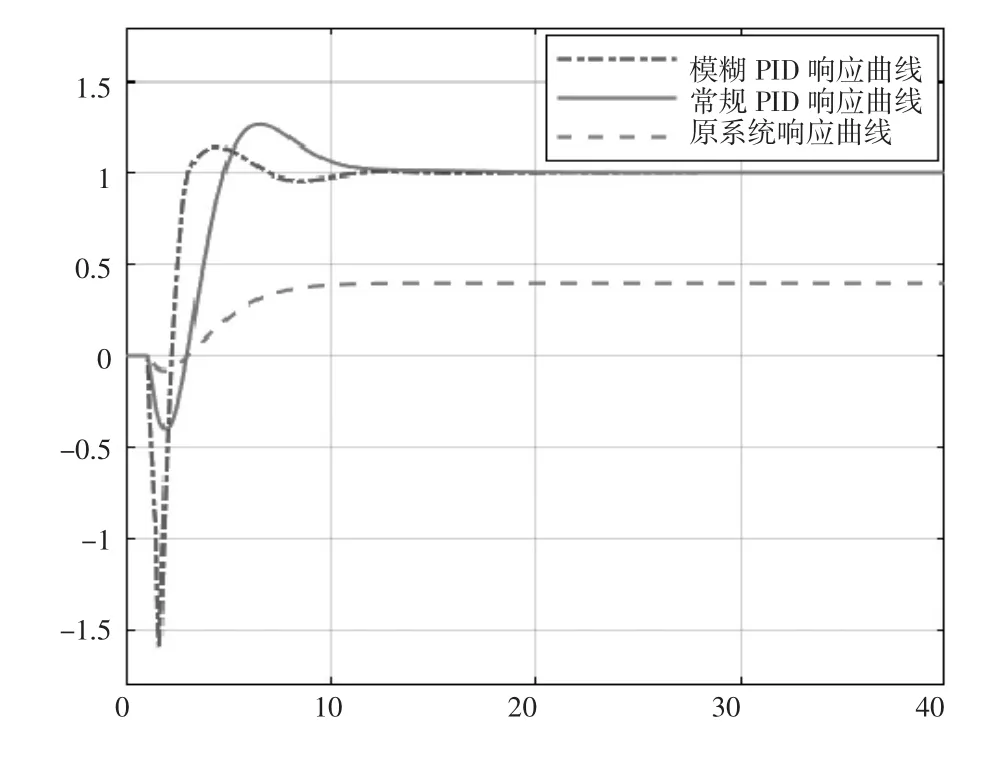
图5 常规P I D和模糊P I D阶跃响应

基于BP神经网络的PID控制器的控制效果如图6-9所示。

图6 kp参数整定曲线

图7 ki参数整定曲线

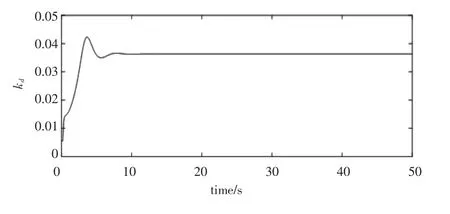
图8 kd参数整定曲线

图9 输出响应曲线

在同等给定的阶跃条件下对常规PID控制、模糊PID控制和BP神经网络PID控制系统的响应曲线进行误差分析、比较，结果见表1。

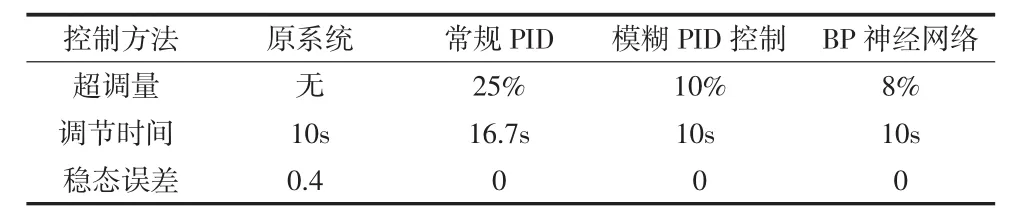
表1 阶跃响应动态性能比较

从各系统仿真图和表1数据对比中可以看出：原系统有稳态误差，阶跃响应的效果很差。用常规PID控制之后，系统的存在超调且达到25%，调节时间很长，但是不存在稳态误差；模糊PID控制的响应速度比较快，超调只达到10%而且调节时间比常规PID缩短了6.7s，没有稳态误差；神经网络PID控制超调下降到了8%，调节时间也缩短到了10 s，稳态误差为零。综上所述，模糊PID和神经网络PID的效果明显好于常规PID，更适合于控制该系统的，但在超调方面BP神经网络的控制效果要稍稍好于模糊PID控制的效果。