聚风风力发电系统的叶片设计方法与仿真模拟研究

2019-06-22鄢瀚

装备制造技术 2019年3期

鄢瀚

（广西大学机械工程学院，广西南宁530004）

0 引言

风力发电是通过将空气中的动能转化为机械能继而发电的可再生能源发电技术。由于风力发电效率与来流风速的三次方成正比，加装聚风结构后风能密度可以有效提升，可以在来流风速较低的情况下进行风力发电[1]，因此提出了在风力机周围加装扩散放大器结构，这种风力机称作聚风型风力机或浓缩型风力机[2，3]，同时具有风速稳定、叶轮受冲击小、噪音低、安全性强、使用寿命长的优点[4，5]。

叶片的外形直接影响风力机功率特性[6]，传统风力机叶片设计方法基于叶素-动量理论，结合GLauert方法或Wilson方法，以每个叶素截面最大输出功率为目标，对叶素弦长与扭角进行计算。

在聚风发电系统中，由于聚风风场与自然风场有较大不同，设计风力发电机叶片时需要考虑来流风场的风速分布，本文在Wilson叶片设计方法上进行改进，研究了自然来流经过聚风装置在风轮安装截面的风速分布，同时考虑到叶片尺寸相对较小，经过聚风后的风速相对较大，叶片设计时，相比于一般叶片，尖速比适量减少。参考田德教授设计的浓缩风能型风力发电机风洞实验[7]，对聚风发电系统叶片设计问题进行仿真模拟研究，将所设计的叶轮与实验所用叶轮进行对比，分析了两种叶片在不同风速下的输出功率。

1 叶片设计理论

1.1 叶素与动量理论

如图1所示，将叶片沿展向划分为若干个微段，这些微段被称为叶素，通过单独分析每个叶素的受力，再沿叶片展向积分，即可得到叶轮整体受力及力矩。动量理论研究了风能向叶轮机械能的转化，确定了来流风速与风轮受力的关系。通过叶素与动量理论结合，得出方程式

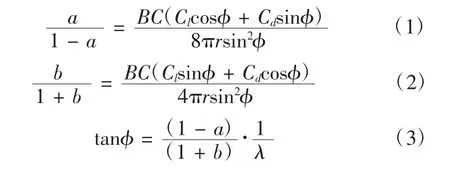
图1 叶素理论模型

1.2 W ilson模型

Glauert方法和Wilson方法是常用的两种叶片设计方法，Glauert方法研究了叶片后涡流对叶片气动性能的影响，并在叶片设计中引入了轴向和周向诱导因子；Wilson方法在此基础之上进一步研究了叶尖损失和升阻比对叶片的影响，是目前设计精度较高一种叶片优化方法[8]。给出叶尖损失Ftip[9]及局部风能利用系数dCp如下

式中，R为风轮半径，λ0为叶尖速比。

以风力设计理论公式为基础，通过调用matlab中的非线性约束优化函数fmincon，以局部风能利用系数最大为目标函数，以式（2）、（3）为约束条件，对诱导因子a、b进行迭代优化，根据诱导因子可以求解各叶素的最佳弦长与扭角。

2 模型修正与设计

由于本文研究对象为聚风风场下的风轮叶片，在Wilson方法的基础上，考虑了小型聚风装置风速分布的不均匀性，设计过程中，在各叶素处不再是以单一初始风速为设计条件，而是以聚风罩为研究对象，以风轮旋转中心为圆心，沿叶片展向各叶素处取点，先得到各叶素处风速分布Vi，从而得到各叶素处速度比，以 λi代替上式 λ，并据此对叶片弦长扭角进行计算。

2.1 聚风结构风场模拟与分析

本文以田德教授所使用的聚风装置为模拟对象，聚风装置模型如图2。通过fluent模拟聚风罩内速度分布。通过Solidworks绘制聚风罩模型，并导入ICEMCFD（The Integrated Computer Engineering and Manufacturing code for Computational Fluid Dynamics），在ICEM中建立圆柱形流场，使用非结构化网格，由于主要研究流体流速经过聚风罩的流速变化，需要在聚风罩附近加密。通过模拟计算得到内部流场速度分布如图3。可以看到聚风罩边缘风速首先被增加，高于中心处风速，之后由于靠近壁面处被减速，经过一段发展，形成中间风速高边缘低的风场。

图2 聚风装置结构及参数

图3 聚风罩内流场风速分布

2.2 叶片参数设计与建模

根据流场速度分布，得到Vi分布如表1。由于研究对象叶轮尺寸较小，且来流经过聚风装置进行加速，叶尖速度相对于来流风速来说相对较小，因此选择叶尖速比λ0=3。选择叶片数量B=3，风轮半径R=0.5。根据上述设计公式，可以得到沿叶片展向各叶素扭角弦长分布，如表2。

表1 叶轮安装截面不同叶素处来流风速

表2 不同半径处各叶素扭角与弦长

所用翼型为NACA63210，通过翼型设计软件profili，可以获得该翼型在某一雷诺数下的升力系数Cl、阻力系数Cd以及最佳攻角。小型风力发电叶轮各叶素可以使用相同攻角α，本文选取雷诺数为2×106，由profili软件得到翼型NACA63210的最大升阻比处攻角为α＝9.5，此时升力系数Cl＝1.2，阻力系数Cd＝ 0.12。

由profili可以得到翼型NACA63210的二维坐标数据结合所得的扭角弦长数据，通过向三维坐标转换，继而可以得到整个叶片的空间坐标数据。再将三维坐标点导入Solidworks，绘制叶根圆以及样条曲线，通过放样功能，能得到叶片模型，最终可以绘制整个叶轮，将其命名为YP型叶轮，图4为Solidworks中绘制得到叶素曲线及叶轮三维模型。

图4 Solidwor k s中绘制叶片及叶轮三维结构

3 仿真模型验证与对比结果分析

3.1 仿真模型及网格划分

本文以田德教授浓缩风能型风力发电机风洞实验为研究对象，并以实验中最佳叶轮NB3型进行仿真模拟，通过仿真结果与实验数据进行对比，验证仿真模型。

NB3型叶片参数如表3，通过坐标转换得到其三维坐标，并在Solidworks中绘制叶轮，将叶轮模型与聚风装置模型导入ICEM，使用非结构化网格，在内部旋转域使用密度较高的网格，并在叶片表面处进行加密。

表3 N B3型叶片参数

3.2 仿真模型验证与结果分析

设置湍流模型为模型，设置边界条件：采用速度入口，压力出口。旋转域与静止域之间建立interface。求解方法选择SIMPLEC，同时监控了叶片进出口流量及叶轮转矩系数。

计算收敛后得到图5为NB3型叶轮速度云图，由速度云图可以看到，流体经过聚风罩，在入口边缘处获得加速，并带动中心处速度的提升，入流风速为，而风轮处流速约为21 m/s，而实验测得风轮处气流流速为风洞风速2.04倍[8]，这证明了模拟得到的风场是可信的。

图5 N B3型叶轮速度云图

而由叶轮转矩系数，在CFD-Post中可以得到风轮所受力矩，进而可以计算风轮功率，风轮功率公式：

式中，P为输出功率，W；T为转矩，N·m；B 为叶片数；N为风轮转速，r/min。

分别计算入口速度4～12 m/s时的风轮功率，根据实验所取发电机效率0.5，计算不同来流风速下发电功率，并取实验图数据进行对比，得到不同来流风速下NB3型叶轮仿真与实验发电功率如图6，来流风速在5 m/s增大到10 m/s时，发电功率会迅速增加，之后会趋于稳定。从变化趋势上看，仿真结果与实验数据基本相同，但仿真更趋于理想状态，而实验可能会因为与理想模型有差别，以及测量误差的影响，而导致最终结果有少许差别。但整体上来看，聚风发电系统三维仿真模型是可信的。