具有连续纤维目标的图像拼接研究

韩子叶，王荣武

(东华大学纺织学院，上海 201620)

0 引言

随着信息的发展与科技的进步，数字化图像处理技术在纺织领域的应用愈来愈广泛，较传统的纺织检测技术更加客观、高效。在进行数字化检测的过程中，通常使用光学显微镜对原始图像进行采集。由于光学显微镜的成像原理等原因，得到的图像会存在清晰度与视野不可兼得的矛盾[1]。如果选择较高的放大倍数，得到的图像更清晰、细节更明显，但是视野较小，无法对材料进行全面的分析；相反，如果选择的放大倍数较低，会得到视野较大的图像，但是清晰度低，不能进行细节观察，得到的分析结果精确度不足。因此，采用图像拼接技术，将多个具有较高放大倍数的小视野图像拼接成为一幅大视野图像，使获得的图像包含清晰细节的同时视野更广。

1 基于SIFT算法的图像拼接

本实验采用2#国际标准羊毛纤维作为实验数据，在BEION M318全自动光学显微镜下，使用4X平场无限远物镜组对图像进行采集，采集到的图像大小均为800×600(x方向为800，y方向为600)。为了将两幅相邻的纤维图像进行拼接，要求两幅图像具有一定的重叠区域。对于M318显微镜的4X物镜组，可设定显微镜载物平台在X轴正方向移动步长为300，采集到的图像如下图1所示。

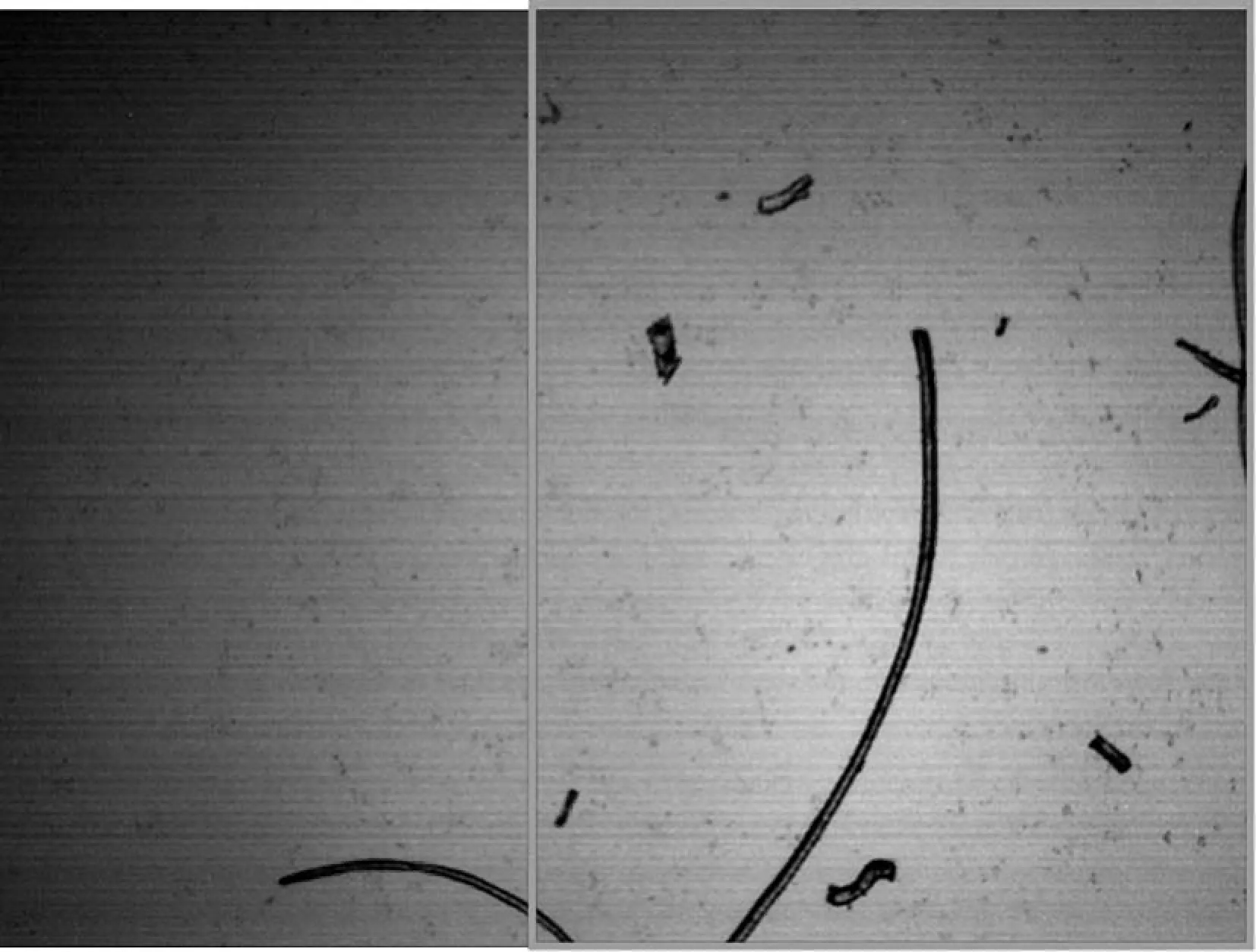
图1 采集到的连续羊毛纤维图像

图像中红色线框所标注的部分即是两幅图像间的重叠区域。如上图1所示，重叠率大致达到了60%。

由图1可以观察到，当图像中纤维分布较为分散时，纤维根数少，包括大片的空白区域，含有的可用信息少。基于上述的图像特点，所采用的图像拼接算法需要具有“多量性”特征，即含有少量的物体也可以检测出大量的特征点用来进行匹配。在众多具有此性质的图像拼接算法中，SIFT算法是典型代表。SIFT算法于1999年由Lowe等人提出后于2004年总结完善[2]，其原理是首先构建图像高斯差分金字塔，在相邻尺度上通过选取指定区域中的极值点来提取候选特征点，再通过三维二次函数拟合精确关键点的尺度和位置，同时消除边缘响应点和低对比度的点。同时为了满足特征点的旋转不变性，为每一个特征点分配一个主方向并且对坐标轴进行变换。将特征点的邻域进行划分，为特征点生成128维的特征向量对其进行描述。之后采用欧式距离作为指标以衡量两个向量间的相似性，在此基础上对图1中的两幅图像进行图像拼接，得到的结果如下图所示。

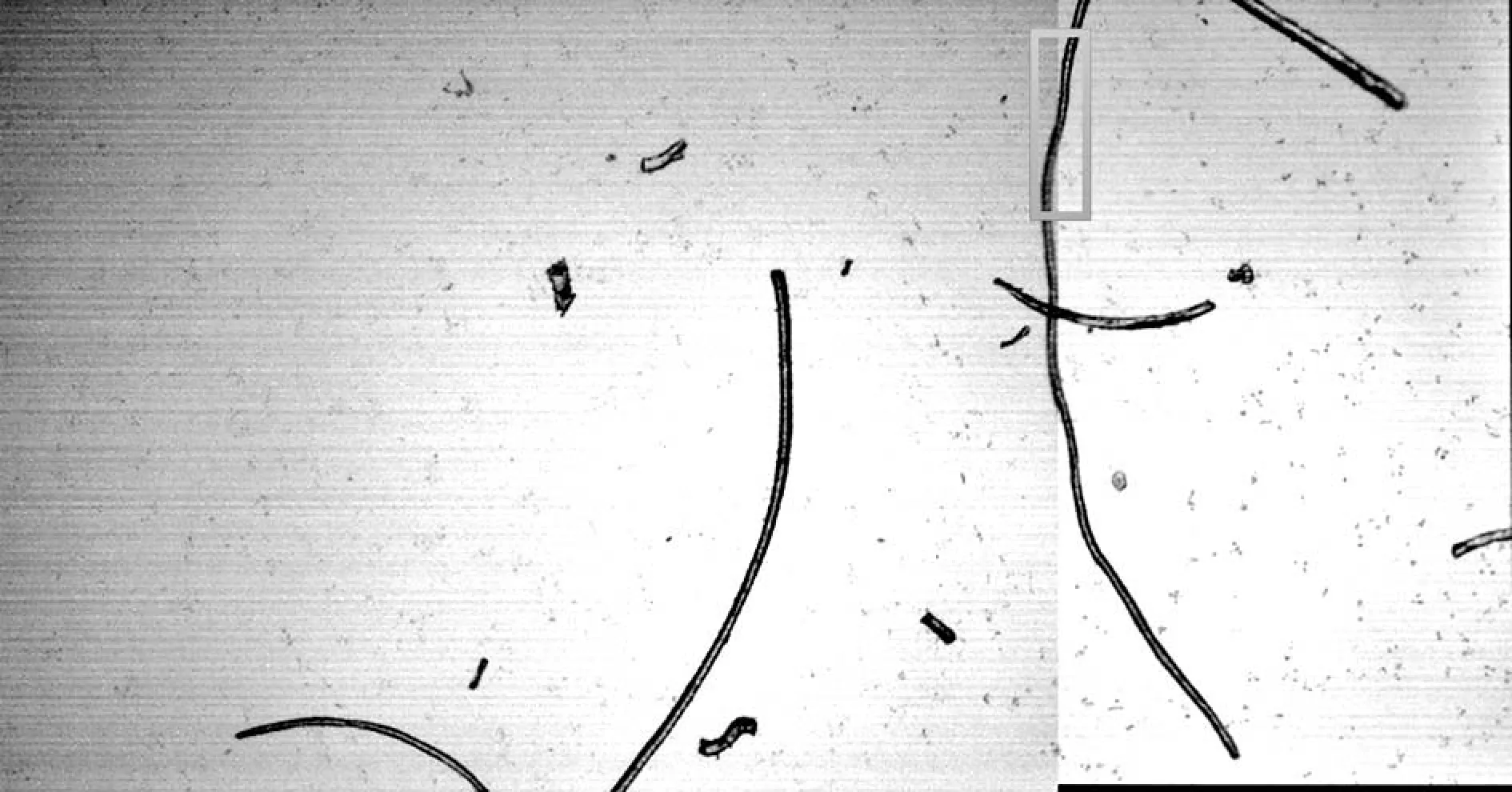
图2 拼接图像

图2中上方图像为图1中两幅图像拼接后原图，图2下方图像为拼接处的局部放大图。可以看出对于毛纤维，当纤维分布稀疏时，SIFT算法的拼接效果良好，但是由于图像采集时点光源影响，两幅相邻图像有光照差异，造成拼接后的图像具有拼接线，因此需要通过图像融合技术消除此线。

2 图像融合

图像融合一方面是要利用待拼接的两幅图像中重叠区域外的不同信息进行互补，使得有用信息在最大程度上保留在配准融合后的图像中，二是消除拼接缝隙，使得两幅图像之间的过渡更加自然、平滑，具有一个良好的视觉效果[3-4]。

本文采用渐入渐出法进行融合。其原理是对位于重叠区域的像素进行加权。权重的选择取决于重叠区域中的像素位置距离其边界的远近，距离越远，权重越小。f1和f2表示待拼接的两幅图像,f表示融合后图像，(x,y)表示像素点的具体坐标，则有：

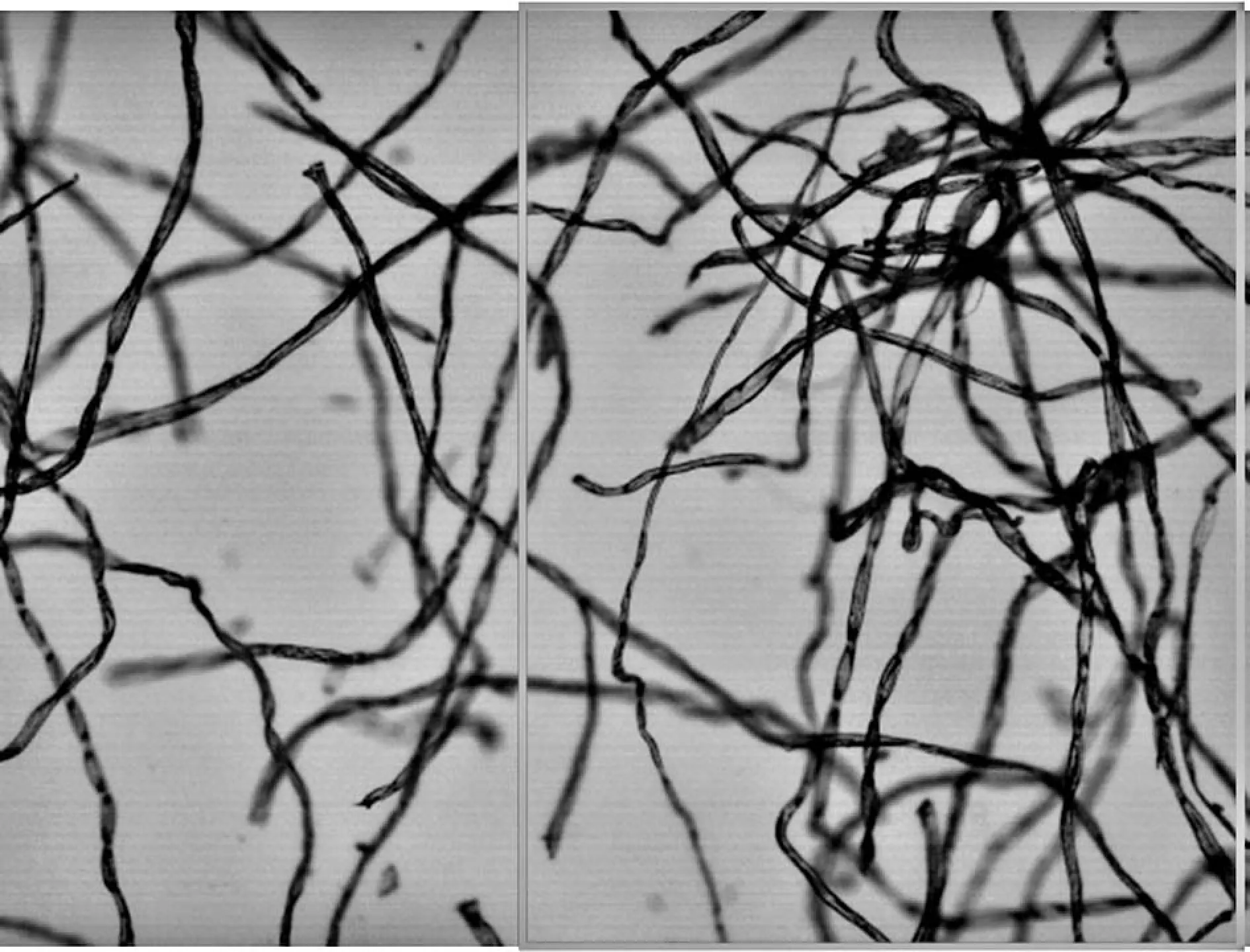
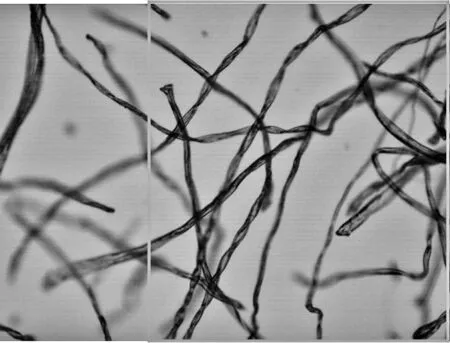
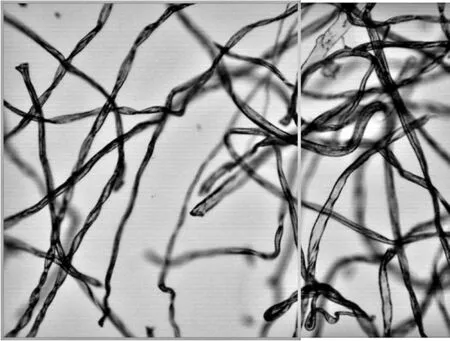
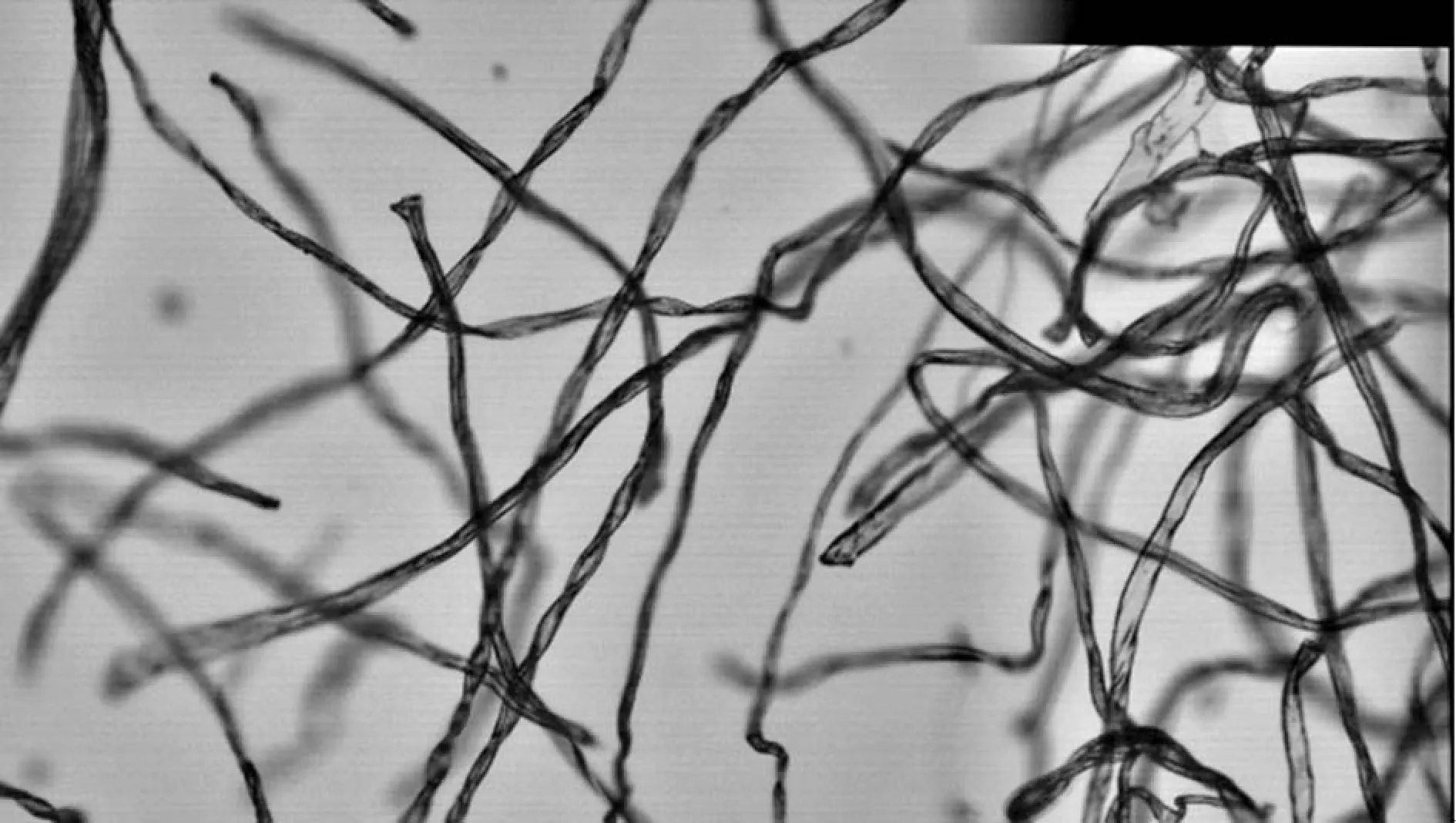
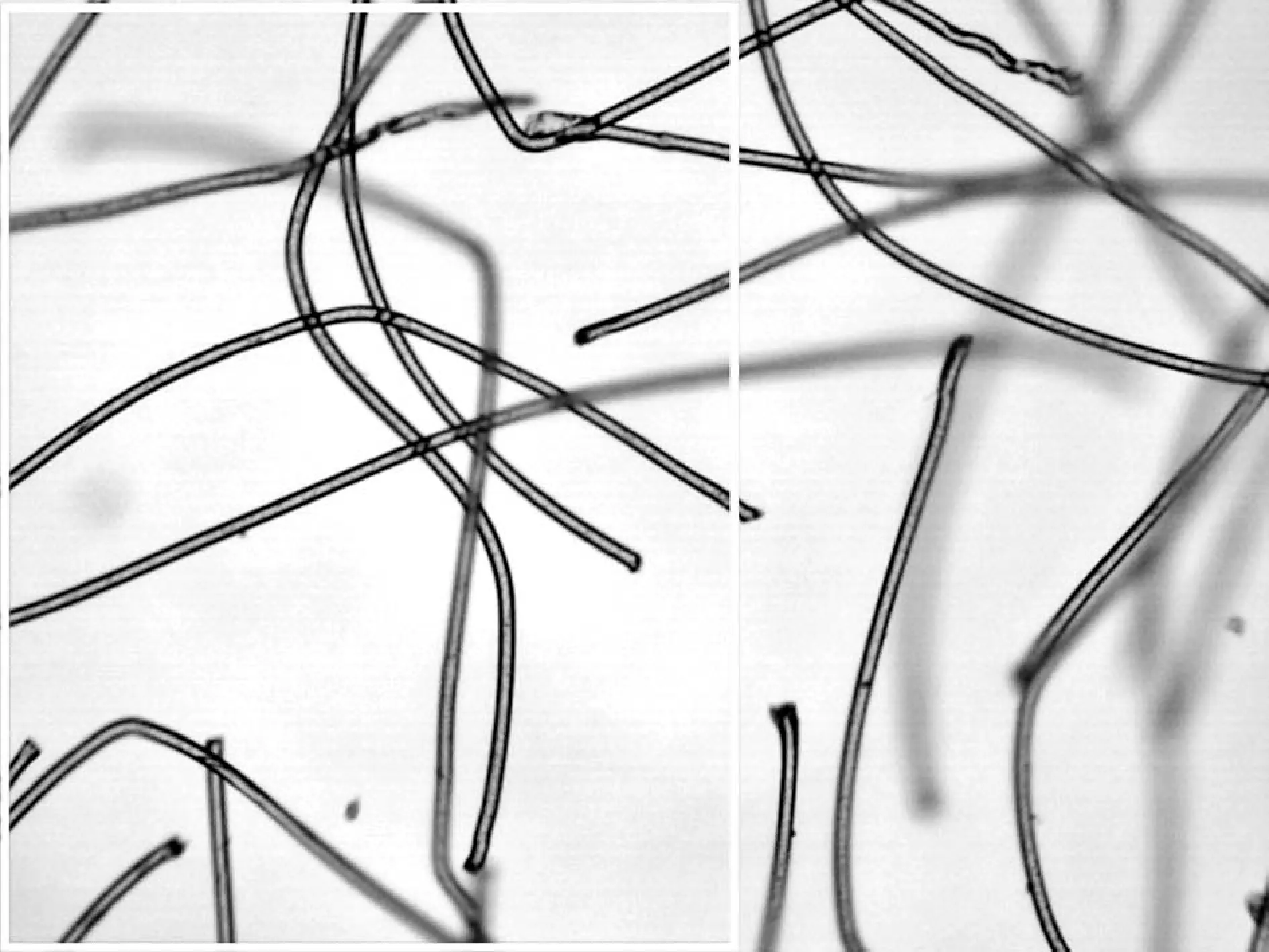
式中，d1和d2表示权重，并且d1+d2=1，0

图3 渐入渐出法原理图

对图2中上方图像进行渐入渐出法融合的结果如下图4所示。

图4 融合效果图

可以看出，经过渐入渐出法融合之后，在拼接处存在着的拼接线已经消失，并且信息没有明显损失，得到了视觉效果良好的拼接图像。

3 广泛性验证

上述实验所采用的图像为羊毛纤维的图像，并且纤维分布稀疏，得到的拼接效果良好，但是由于纺织材料的广泛性，其纤维原料多样、纤维分布的形式多样以及显微镜的倍数多样。因此，需要在不同的情况下对此算法进行验证实验。本实验采用天然纤维中的棉纤维、化学纤维中的涤纶纤维以及非织造材料等图像进行验证。

3.1 使用棉纤维图像进行验证

棉纤维具有良好的吸湿和透气性能，并且手感柔软，透气性好，被广泛地应用于纺织领域中。在上文采用羊毛纤维进行实验时，图像中纤维分布稀疏。因此，为了验证算法在纤维分布密集时的拼接以及融合效果，在使用棉纤维图像进行验证时，使纤维分布密集，并在4X物镜组与10X物镜组下分别获取图像。

图5 4X物镜组下采集的连续两幅密集棉纤维图像

在4X物镜组下对分布密集的棉纤维进行图像采集，得到连续的两幅图像，其中纤维含量多，包含的信息更为复杂，如图5所示。拼接结果以及拼接结果的验证如下图6所示。

(a)

(b)

图6(a)为图5中两幅图像进行拼接的结果，图6(b)中则包含了拼接图像中拼接线周围完整的图像信息，在(a)、(b)两幅图像中于拼接线周围选择三个同样的特征点进行连接，得到了两个全等三角形，表明SIFT算法适用于低倍数下密集纤维图像的拼接，会得到良好的拼接效果。对6(a)采用渐入渐出法进行图像融合的结果如下图7所示。

图7 图6(a)中图像融合后结果

由融合后图像与融合前图像进行对比可以看出融合效果良好，既保留了非重叠区域的图像信息，使其完整，又消除了拼接缝隙，使整个图像过渡自然。

图8 10X物镜组下采集的连续两幅密集棉纤维图像

由图8可以看出，与低倍物镜组下采集到的纤维分布密集时的图像相比，高倍镜下多焦面现象更为明显，当纤维数量较多时，在空间中产生“堆叠”，即同一幅图像中纤维存在不同焦面上，无法同时表现出清晰的状态，对图像进行连续采集时，位于两幅图像中的同一点并不能保证会是同一个清晰状态，因此增加了拼接难度。对图8中两幅连续图像进行拼接，结果与拼接效果验证如下图9。

(a)

(b)

图9(a)为采集到的10X物镜下连续两张密集棉纤维图像进行拼接的结果，图9(b)则为4X物镜下采集到的同位置图像，包含了完整的图像信息，在(a)(b)两幅图像中于拼接线周围选择三个同样的特征点进行连接，得到了两个相似三角形，表明SIFT算法对于尺度具有良好的鲁棒性，适用于高倍数下密集纤维图像的拼接。对图9(a)使用渐入渐出法进行图像融合的结果如下图10所示。

图10 图9(a)中图像融合后结果

由融合结果可以看出，该融合算法同样适用于具有多焦面现象的纤维密集分布图像。

3.2 使用涤纶图像进行验证

涤纶纤维是一种常见的化学纤维，具有耐冲击性、弹性好等特点，被广泛地应用于纺织领域。本文分别使用4X物镜组和10X物镜组对涤纶纤维图像进行采集，对本文中的算法进行验证。

图11 4X物镜组下采集的连续两幅涤纶纤维图像

拼接结果以及拼接结果的验证如下图12所示。

(a)

(b)

图12(a)为图11中两幅图像进行拼接的结果，图12(b)中则包含了拼接图像中缝隙周围完整的图像信息，同样在4X物镜组下拍摄，在(a)、(b)两幅图像中于拼接缝隙周围选择三个同样的特征点进行连接，得到了两个相等三角形，表明SIFT算法适用于低倍物镜组下涤纶纤维图像的拼接。

在10X物镜组下对涤纶纤维进行采集的图像如下图13。

图13 10X物镜组下采集的连续两幅涤纶纤维图像

拼接结果以及拼接结果的验证如下图14所示。

(a)

(b)

图14(a)为采集到的10X物镜下连续两张涤纶纤维图像进行拼接的结果，图14(b)中则包含了拼接图像中缝隙周围完整的图像信息，在4X物镜组下拍摄，在(a)、(b)两幅图像中于拼接缝隙周围选择三个同样的特征点进行连接，得到了两个相似三角形，表明SIFT算法适用于高倍物镜组下涤纶纤维图像的拼接。

3.3 非织造材料图像

非织造材料是由纤维直接构建而成，因此非织造材料图像亦是纤维目标图像。因为本实验图像由光学显微镜获取得到，由于透光的问题，要求非织造材料的厚度在一定范围内，便于光透射进行图像采集。因此，本实验采用纺粘非织造材料进行拼接，并对拼接效果进行验证。

本实验对纺粘非织造材料在20X物镜组下的图像进行采集拼接，在20X物镜组下对纺粘非织造材料进行采集的图像如下图15。

图15 20X物镜组下采集的连续两幅纺粘材料图像

拼接结果以及拼接结果的验证如下图16所示。

(a)

(b)

>图16(a)为采集到的20X物镜组下两张连续的纺粘非织造材料图像进行拼接的结果，图16(b)中则包含了拼接图像中拼接线周围完整的图像信息，在10X物镜组下采集得到，在(a)、(b)两幅图像中于拼接线周围选择三个同样的特征点进行连接，得到了两个相等三角形，表明SIFT算法适用于高倍物镜组下纤维信息复杂的纺粘非织造材料图像的拼接。

4 结论

使用渐入渐出法对SIFT算法拼接后的图像进行融合，可以消除因光照差异等原因产生的拼接线。通过使用棉纤维图像、涤纶纤维图像以及纺粘材料的图像对上述算法进行验证，该算法可以广泛地应用于纺织领域。通过对纤维图像进行拼接，使纤维目标更加完整化，获得更加精确全面的纤维信息，在数字化检测的过程中得到应用，如增加纤维直径的测量精度；扩展了图像视野，可以得到材料本身更加完整的信息，如材料的孔隙率、取向度、混纺比等性能。