基于阿里云的四维弹簧模型并行运算性能
2019-06-21赵高峰陈华
赵高峰,陈华
(天津大学 建筑工程学院;水利工程仿真与安全国家重点实验室,天津 300072)
由于具有可重复、经济及参数可控等优点,数值模拟已经成为理论分析和物理实验之外的第3种研究方法[1-3]。数值模拟不但被广泛应用于隧道等地下工程在不同工况下的稳定性分析,而且被用来研究特定工程灾变问题的内在力学机理。例如,唐春安等[1]采用RFPA软件对隧道洞室周边的分区破坏机理和演化规律进行了研究,吴顺川等[2]采用三维离散元软件研究了隧道岩爆的机理。上述两个数值模拟案例分别采用了基于连续介质的有限元法和基于离散介质的离散元法。连续介质方法的基本思路是先建立求解对象的偏微分方程,然后,通过数学离散方法求解,是一种自顶向下的方法。由于其连续假设,连续介质方法在求解动态断裂等问题时具有一定的局限性。将损伤模型引入连续介质方法可增强其求解渐进动态破坏的能力,例如RFPA软件[1]及LSDYNA软件[4]采用了类似单元生死法来实现对材料渐进破坏的描述,并已成功应用于岩石动态破坏及实际工程的计算。然而,这种关于破坏的处理方式没有精确考虑破裂面的形态以及再接触,因此,该方法对破坏后的描述可能会有偏差[5]。基于离散介质的数值方法则考虑了破裂面的分离和再接触,更适合于岩石动态破坏问题,其中,最为著名的是Cundall等[6]提出的离散元和Shi[7]提出的非连续变形分析方法DDA。作为离散数值计算方法的一种,Lattice Spring Model (LSM)由亚历山大博士于1941年最早提出[8],但由于泊松比限制问题,LSM发展一直很缓慢。为了解决该问题,Distinct Lattice Spring Model (DLSM)引入了多体剪切弹簧[8],该模型已被成功应用于岩石与煤的动态破坏研究[9-11]。最近,研究者提出了另一种解决方法,基于经典LSM引入额外维相互作用,称之为四维弹簧模型(Four-lattice spring model,4D-LSM)[12]。4D-LSM的基本元件是由弹簧键连接的颗粒,通过弹簧键的变形和破坏来反映固体的宏观力学响应。4D-LSM这种自底向上的建模方式与离散元类似,其单元(颗粒)数量必须达到一定规模才能得到足够真实的模拟结果。因此,4D-LSM有庞大的计算需求,传统的个人电脑已经不能满足,高效的并行计算是唯一的解决办法。
目前,并行计算器件主要分为多核CPU和GPU,而主要计算平台是超级计算机。超级计算机拥有多个节点,每个节点一般是可以单独实现CPU多核并行和(或)GPU并行的计算机,节点间通过网络连接实现消息传递,从而将计算资源整合利用,并达到超高的计算性能。全球超级计算机Top500中,目前排名第一的超级计算机“Summit”由4 608个节点组成,每个节点搭载2个“Power9”CPU和6个“NVIDIA Tesla V100”GPU,CPU核心数量为202 752,GPU流处理器数量超过1.4亿,其峰值性能为200PFLOPS[13]。近年来,GPU计算发展十分迅速[14],但是GPU计算并不能取代CPU计算,比如CPU更擅长处理逻辑控制密集任务,CPU多核并行仍然是一种便捷、可靠并且广泛使用的高性能计算方式。实现CPU多核并行主要依靠应用程序接口,例如OpenMP(Open Multi-processing)等[15]。OpenMP是基于共享内存的应用程序接口,提供了对并行算法的高层抽象描述,非常适合多核CPU计算机的并行程序设计。OpenMP的显著特点是精简、易用,只需要在串行代码中加入简单的pragma指令即可实现并行,因此,OpenMP的使用非常普遍,例如4D-LSM和DLSM就采用OpenMP实现了多核并行[12,16]。
高性能计算通常以高性能计算机为依托,但超级计算机硬件的高昂费用和固定资产属性常导致高性能计算的使用成本较高。近年来,计算领域中面向服务的“云计算”为解决这个问题提供了可能。云计算是指通过网络按需提供虚拟计算资源和解决方案的有偿服务,相对于传统的计算模式,其主要优点是配置灵活、方便快捷、管理投入少等。例如,由“阿里云”提供的弹性云服务器类型有通用性、计算型、内存型等,CPU核数从2核到160核不等,内存从4 GB到1 920 GB不等[17],付费方式也有按量计费、按时间计费等不同选择。笔者主要研究多核4D-LSM在云计算及常规多核工作站和个人电脑上的并行运算性能,通过大量数值模拟计算来研究线程数量、硬件配置、求解问题类型等对4D-LSM并行计算时间的影响,进而找到4D-LSM在“阿里云”计算环境下的极限规模和瓶颈,最后,通过4D-LSM求解脆性材料的三维破裂问题来展示离散数值计算方法和并行计算相结合带来的优势。
1 四维弹簧模型
1.1 基本原理
在经典物理学中,空间是三维的,时间作为第四维,它们共同构成了四维时空。有些研究者为了统一自然界的4种基本力,通过引入一个额外的空间维度,提出了五维时空。4D-LSM借鉴了五维时空理论。4D-LSM模型的构建过程如图1所示。图1(a)中,三维空间中的立方体晶格模型能够再现各向同性弹性,其泊松比固定为0.25。该原始模型的弹簧键有两种,即正弹簧(例如AB)和对角弹簧(例如AC),其刚度系数均为k。图1(b)所示为原始模型在第四维的“平行体”,对于给定的质点A,其“平行体”即为A′,“平行体”模型的构造和弹簧刚度均与“本体”模型相同。然后,利用第四维相互作用(弹簧键)连接“本体”和“平行体”,如图1(c),具体规则为:“本体”模型的一个弹簧(例如A-B)产生4个相应的四维弹簧(A-A′、B-B′、A-B′和A′-B)。
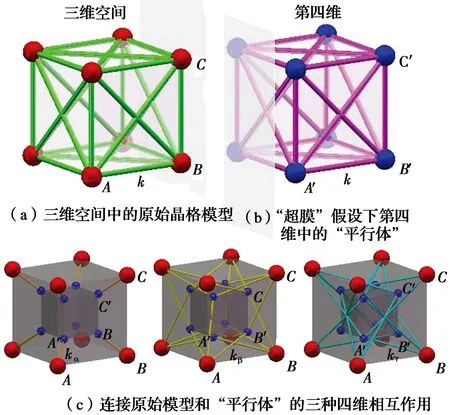
图1 四维弹簧模型的构建过程[12]Fig.1 The model building process of
1.2 系统方程
在4D-LSM中,假定三维世界是一个四维超膜,离散的四维颗粒由弹簧键连接。4D-LSM的描述和证明详见文献[12],这里只关注对实现并行化必不可少的有关方程。四维颗粒的空间位置和运动参数表示为
xi=(xiyiziϑi)T
(1)
(2)
(3)
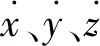
(4)
式中:t为时间;Δt为时间增量。以相同的方法,可以得到颗粒的速度公式
(5)
颗粒i和颗粒j之间四维距离为
(6)
如果这些颗粒通过刚度为k的弹簧连接,那么颗粒j对颗粒i的作用力为
(7)
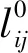
(8)
式中:mi为颗粒i的质量;gx、gy和gz为重力加速度。在4D-LSM中,假设牛顿第二定律也适用于第四维,则颗粒i的加速度为
(9)
式(1)~式(9)是实现4D-LSM并行化涉及的所有基础性计算。
1.3 模型参数选取
对于立方体四维晶格,有3种类型的四维弹簧,刚度分别为kα、kβ、kγ。对于弹性各向同性体,它们的刚度值需满足关系[12]
(10)
式中:λ4D为四维刚度系数;k为三维弹簧的刚度,k用式(11)计算。
(11)
式中:V为三维晶格模型的代表体积;E为弹性模量,li为三维晶格模型的初始弹簧长度;η为尺度参数。η可用式(12)计算[12]。
0.416 136 15λ4D+1.003 692 23
(12)
四维刚度系数λ4D也可以由泊松比得到[12]。
λ4D=-211.134 937 79v3+162.846 558 51v2-
55.424 497 19v+6.929 022 11
(13)
式中:v是泊松比。结合式(10)和式(13)可算出式(7)所需的力学参数(弹簧刚度)。这些参数都是预先计算的,与4D-LSM的计算循环无关,因此,参数计算部分不参与并行。更多细节和数学证明可以在4D-LSM的原始文献[12]中找到。
1.4 OpenMP多核并行

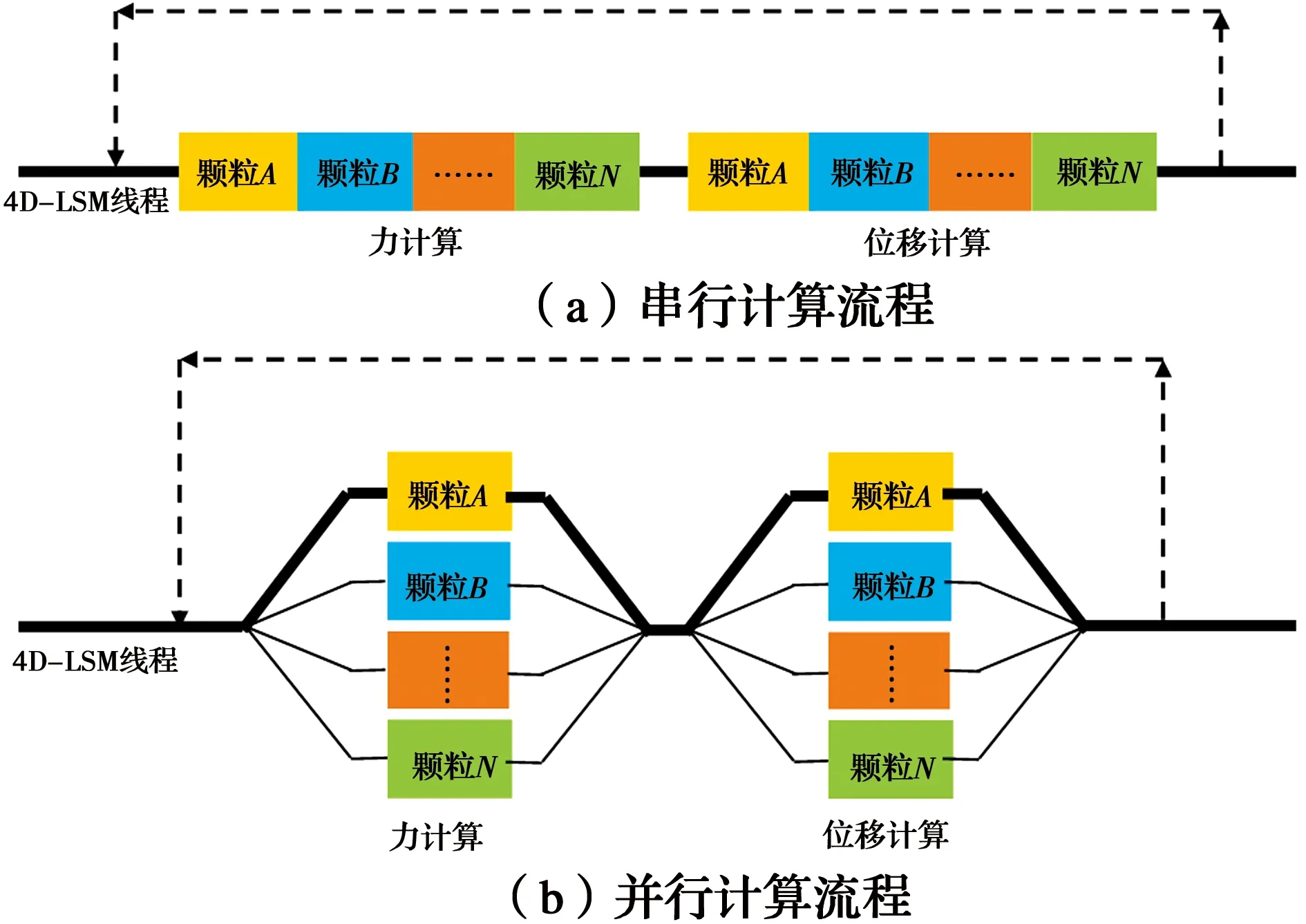
图2 4D-LSM的分叉并行策略Fig.2 Fork/Join parallel strategy of
1.5 计算模型
采用两种4D-LSM计算模型,分别对应弹性问题和破坏问题。如图3所示,模型外观均为立方体,选用的颗粒直径为1 mm。第1计算模型为立方体单轴压缩试验,底端在竖直方向被固定,顶端施加竖直向下的位移荷载,整个模拟过程不破坏,属于线弹性问题。第2个问题是爆炸开裂模型,模型中心有球形空洞(绿色部分),冲击荷载施加在球体的内表面,属于动态破坏问题。每个计算模型采用不同规模,立方体边长分别为20、50、100、150、200、250、300 mm,因此,最大的模型颗粒数达到2 700万(300×300×300)。
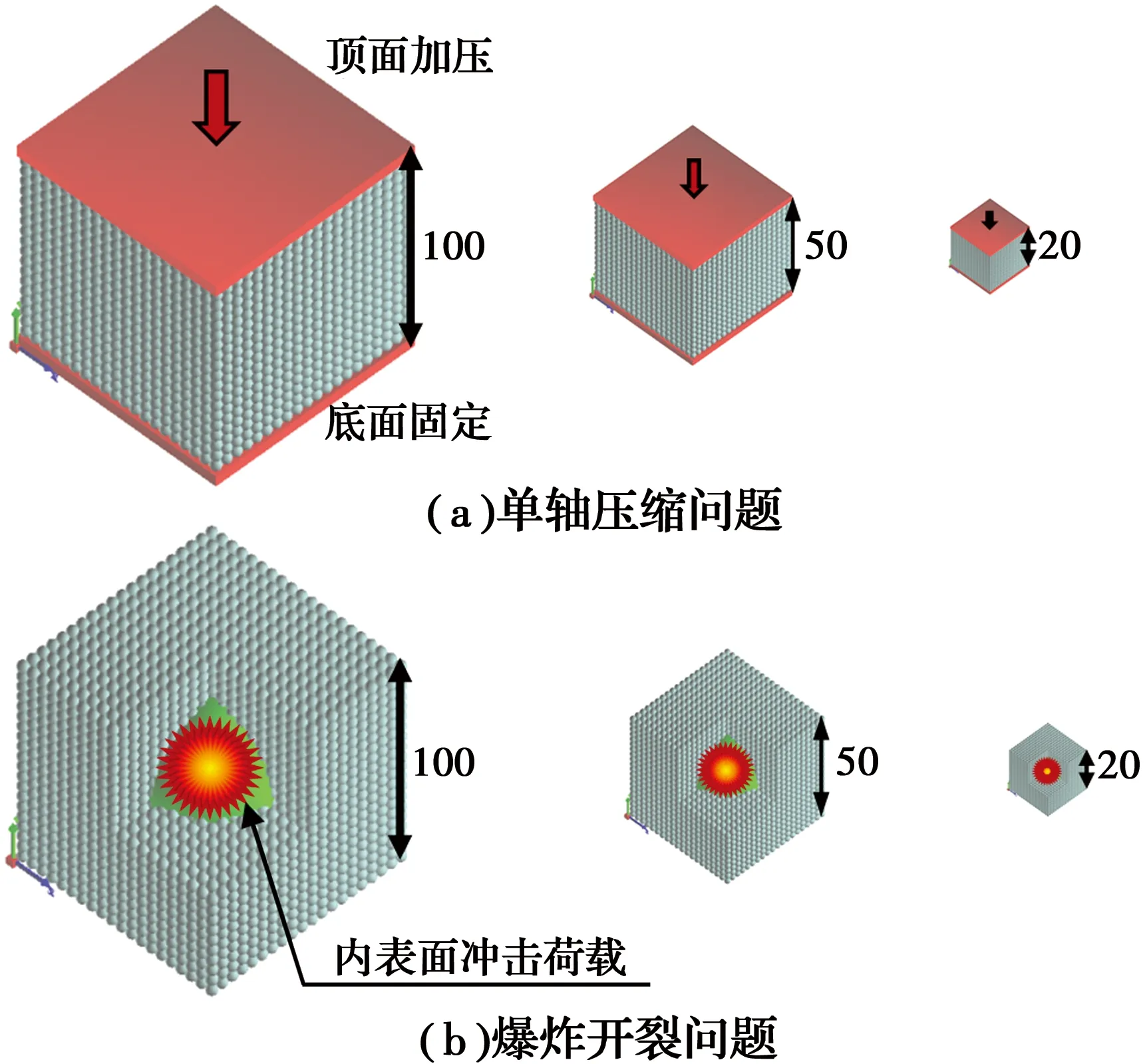
图3 两种4D-LSM计算模型Fig.3 Two kinds of 4D-LSM computing
1.6 并行性能分析
云服务器是一种虚拟的计算机,根据客户的需求可以有不同配置。如果用户选用的云服务器操作系统与自己本地计算机的操作系统一样(如Windows系统或者Linux系统等),那么,云服务器的操作体验与本地计算机几乎没有区别,能够在本地机运行的程序同样可以在云服务器上运行,不需要做任何额外的更改,本文涉及的基于OpenMP的4D-LSM也是如此。如表1所示,选用的云服务器(CS)具有64核心、128 GB内存容量,CPU频率是2.5 GHz。线程测试选用的是单轴压缩模型,模型的大小有3种,边长为50、100、150 mm,分别记为“Cube_50”、“Cube_100”和“Cube_150”,相应的颗粒数为12.5万、100万和337.5万。将每一个模型在不同的计算机上采用不同的线程数进行重复计算,记录每次计算的时长,并换算出加速比,加速比定义为单线程计算时间与多线程计算时间的比值。
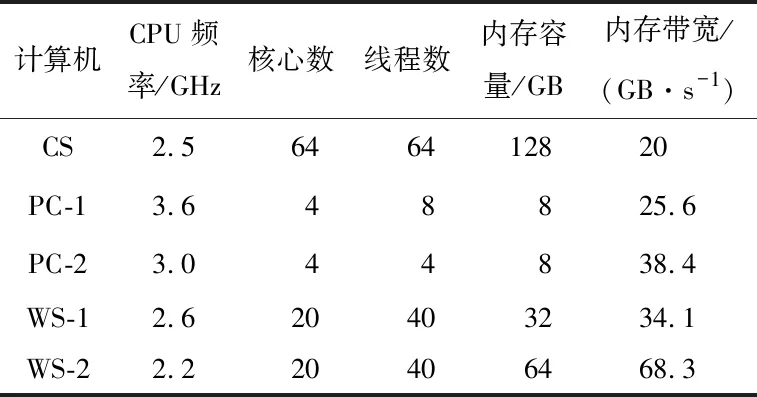
表1 计算机主要参数Table 1 Main parameters of the computers
阿里云上的测试结果如图4所示,最大加速比约为16.8×。单从最大加速比来看,云计算优于两台工作站WS-1和WS-2(见图8,最大加速比约为9.0×),并且,云计算还有使用灵活、无需维护等优点。但是,相较于本地计算资源,云计算也有不足之处。首先是性价比的问题,测试用的云服务器按时间计费,费用约为350元/d,而工作站WS-2的一次性投入约为5万元,该费用只能购买该云服务器5个月左右,但通常情况下,一台工作站的性能至少可以在3年内保持相当的竞争力。数值计算方面的科研工作,经常需要修改模型的参数,这样的重复计算是对云计算资源的浪费。因此,最合理的方式是利用本地计算资源调整数值模型,然后利用云服务一次性完成大规模计算。其次,大规模计算必定涉及到大量的数据存储问题,由于云服务的存储具有时效性,也不方便进行后处理工作,因此,如何快速将海量数据保存到本地存储空间是云服务应用于数值分析计算面临的另一个问题。
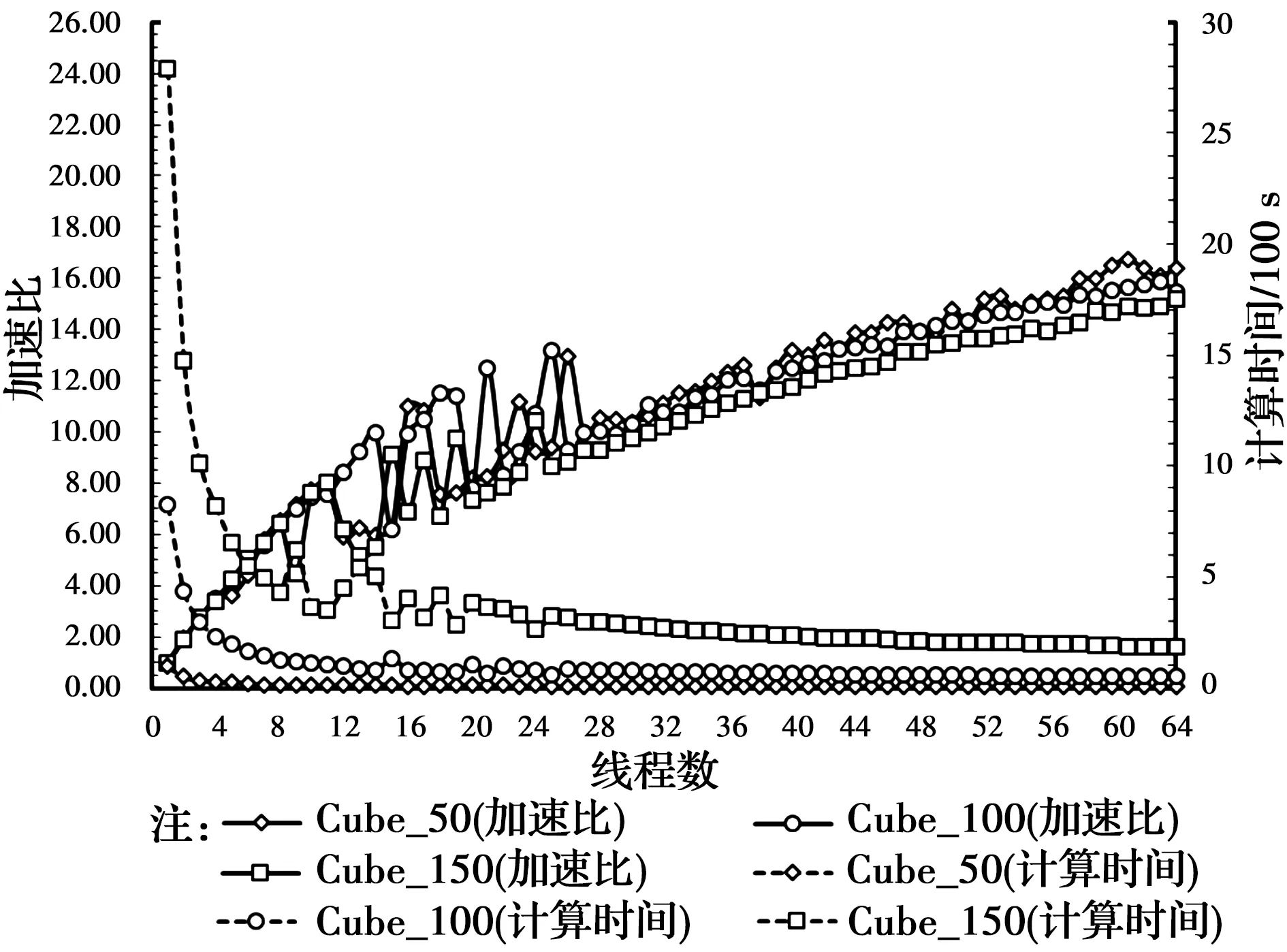
图4 阿里云计算环境下4D-LSM并行效率测试结果Fig.4 Parallel efficiency test results of 4D-LSM in Alibaba
PC-1、PC-2、WS-1和WS-2的测试结果如图5~图8所示,最大加速比分别为2.6×、3.2×、10.8×和9.1×,随着线程数的增加,计算速度总体上呈加快的趋势。PC-1是4核8线程,由图5可知,当线程数超过4以后,加速效果明显下降,例如“Cube_150”的模型使用2线程、4线程和8线程时的加速比分别为1.84×、2.54×和2.6×,意味着加速比从2线程到4线程的增幅为38%,而从4线程到8线程的增幅仅为15%,这说明物理核心的加速效果远远超出超线程技术的加速效果。两台工作站WS-1和WS-2是20核40线程的双路计算机,由图7、图8可知,当线程数超过20以后,加速效果的提升即开始放缓。更值得关注的是,对于WS-1和WS-2这两台双路计算机(每个CPU有10个核心、两个CPU共20核),10线程和20线程的加速效果几乎相同,例如WS-1上“Cube_150”模型使用10线程和20线程时的加速比分别为7.1×和7.7×,当线程数介于10和20之间时,加速比呈现先降后升的“凹”型曲线,计算资源的增加却适得其反。
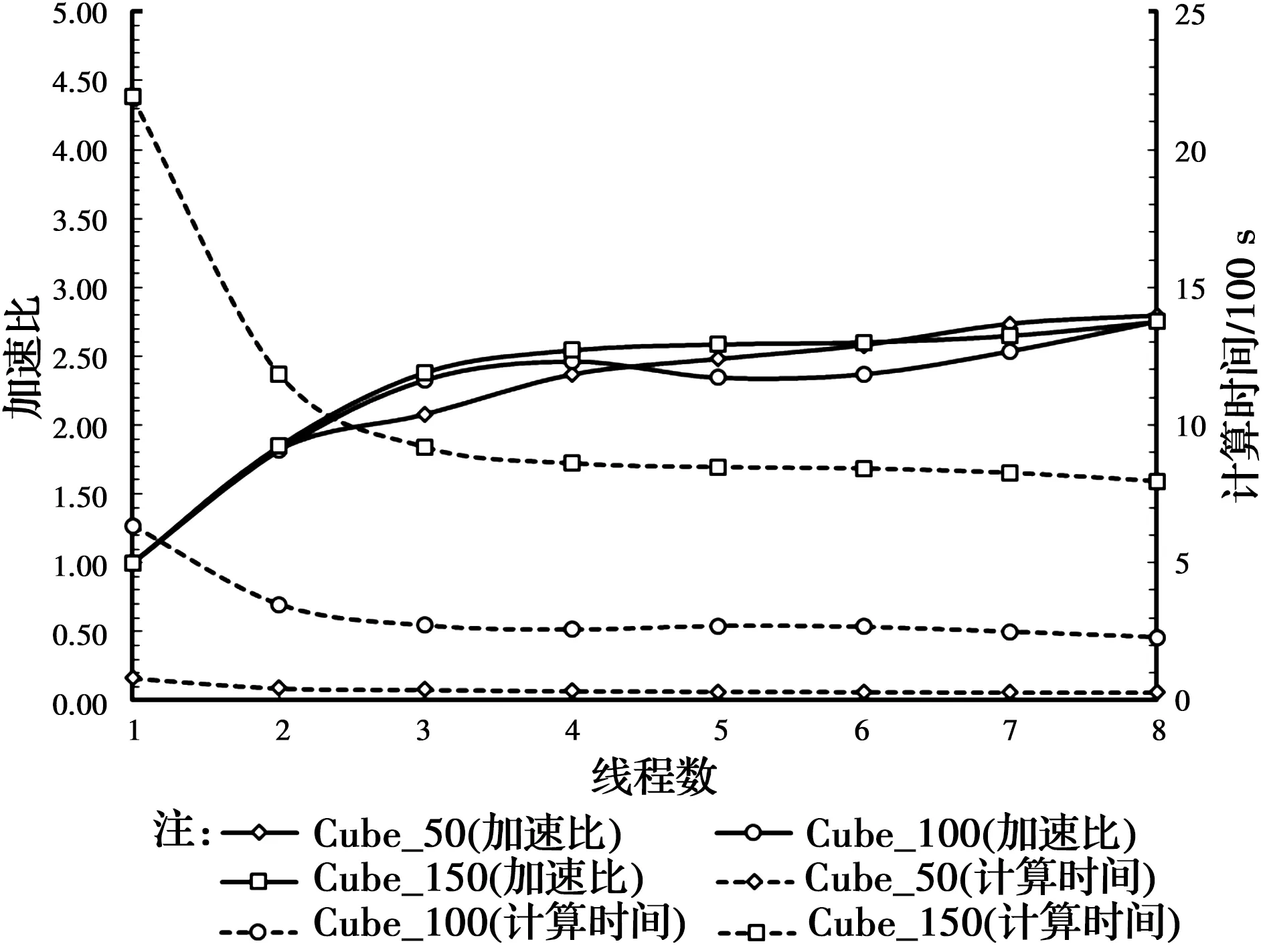
图5 4D-LSM在PC-1上并行效率测试结果Fig.5 Parallel efficiency test results of 4D-LSM on
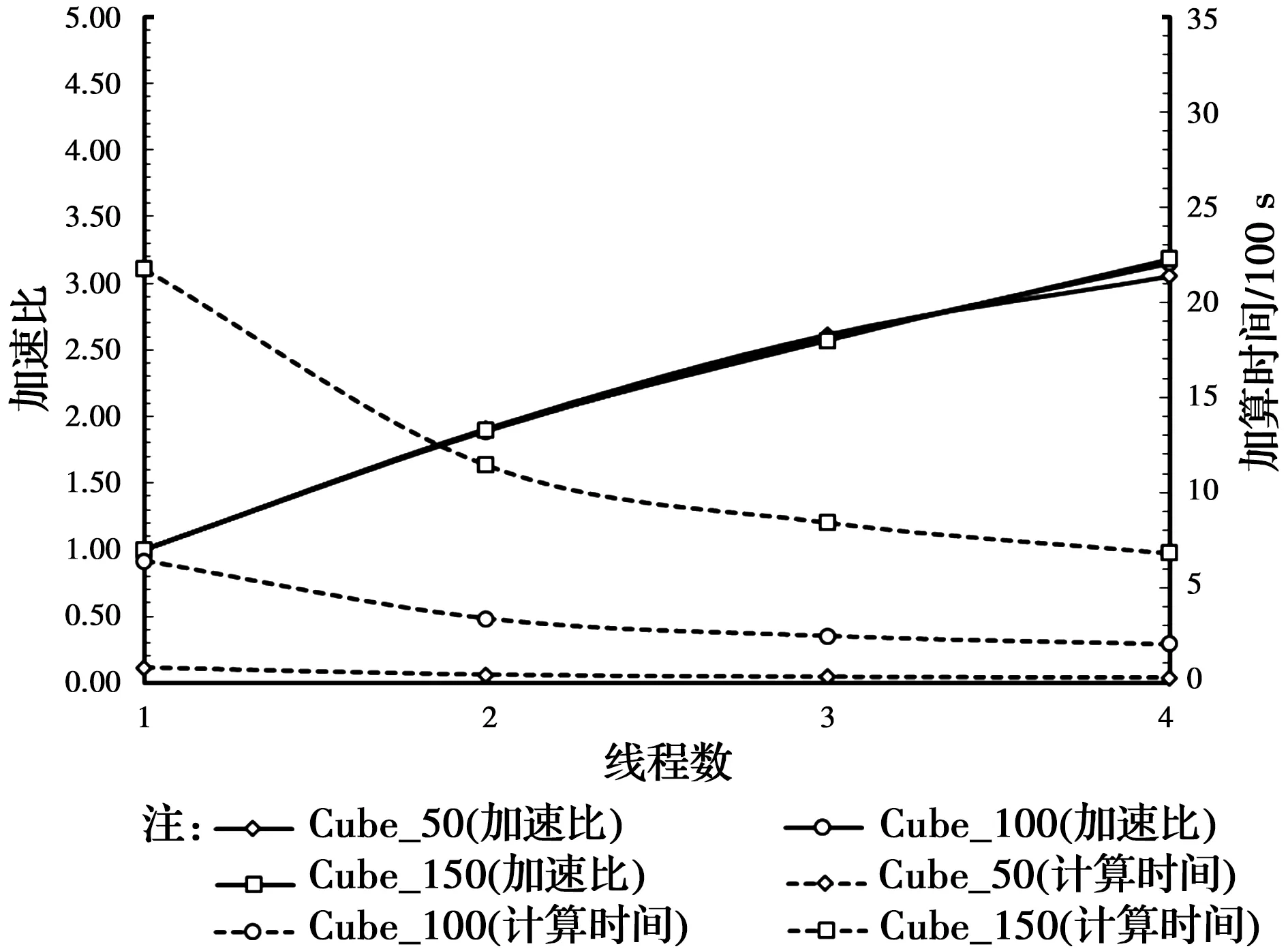
图6 4D-LSM在PC-2上并行效率测试结果Fig.6 Parallel efficiency test results of 4D-LSM on
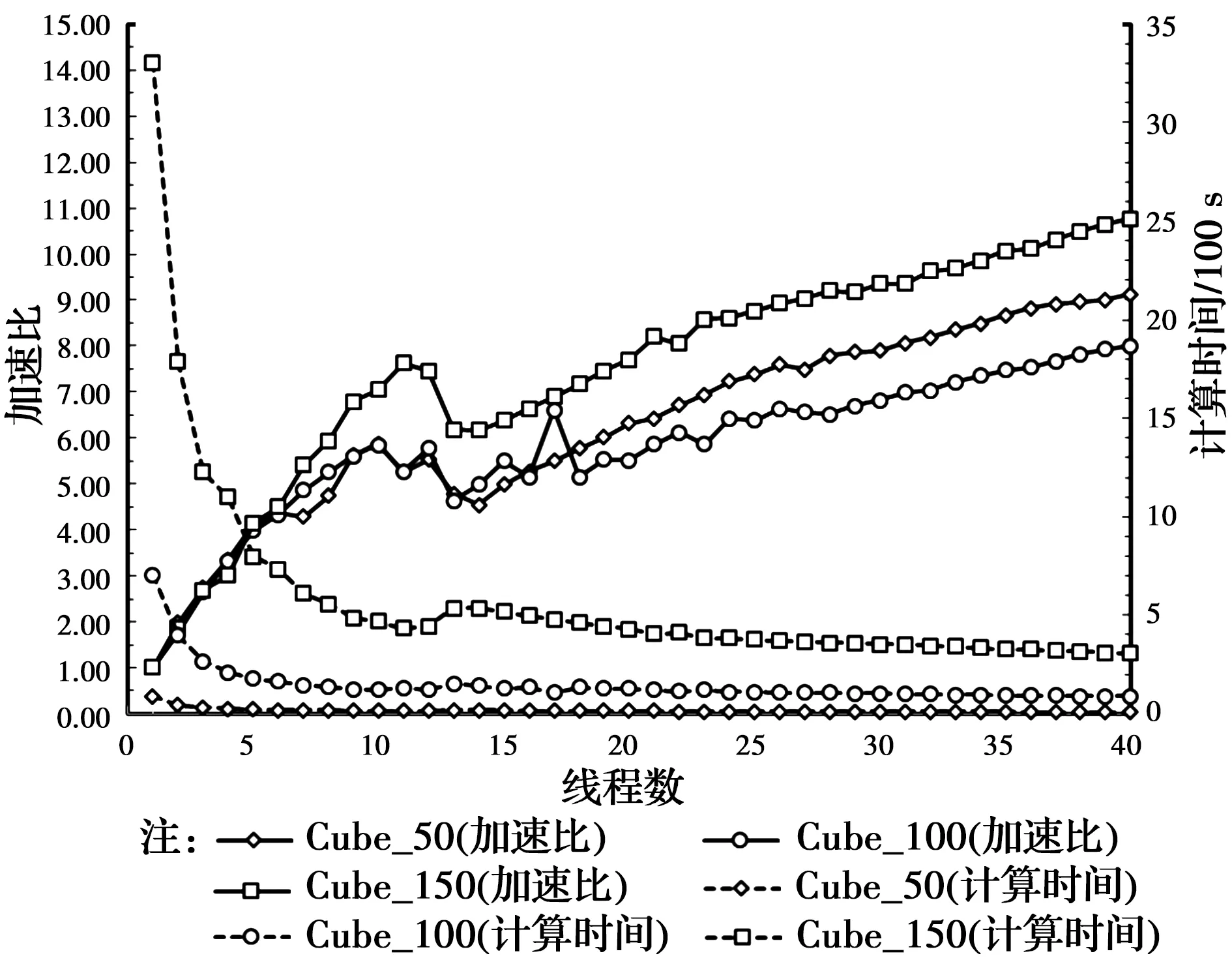
图7 4D-LSM在WS-1上并行效率测试结果Fig.7 Parallel efficiency test results of 4D-LSM on
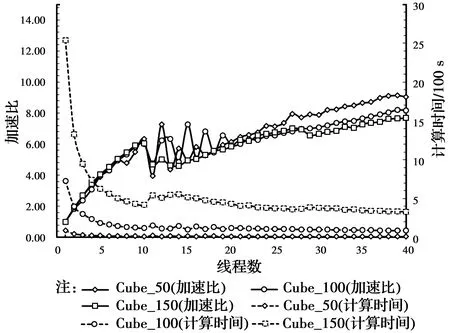
图8 4D-LSM在WS-2上并行效率测试结果Fig.8 Parallel efficiency test results of 4D-LSM on
1.7 并行性能影响因素及极限运算分析
1.7.1 求解类型的影响 4D-LSM模型中,破坏的颗粒在每一步的计算过程中都会进行动态接触检索,当有其他颗粒接触到该破坏颗粒时,这两个颗粒之间会产生一个新的特殊弹簧键,该弹簧键并不能受拉,其目的只是为了防止破坏颗粒由于运动而穿透其他颗粒,相对于非破坏模型,破坏模型的颗粒检索将会消耗额外的时间。为了研究加速比与求解类型的关系,选用单轴压缩模型和爆炸开裂模型进行对比,前者代表弹性(Elastic)问题,后者代表破坏(Fracture)问题,模型外观均为立方体且边长均为100 mm,计算机选用工作站WS-2,测试结果如图9。对于线程数与计算效率的总体关系,破坏模型与前述弹性模型一致,但是,对比弹性模型与破坏模型的加速比发现,随着线程数的增加,两者的加速比差距越来越大,最终,使用40线程时弹性模型的加速比达到9.0×,而破坏模型相应的加速比为5.8×,仅为前者的64%。总之,并行化的4D-LSM求解破坏问题所获得的加速效果要低于非破坏问题,使用的线程数越多,这种差距越明显。
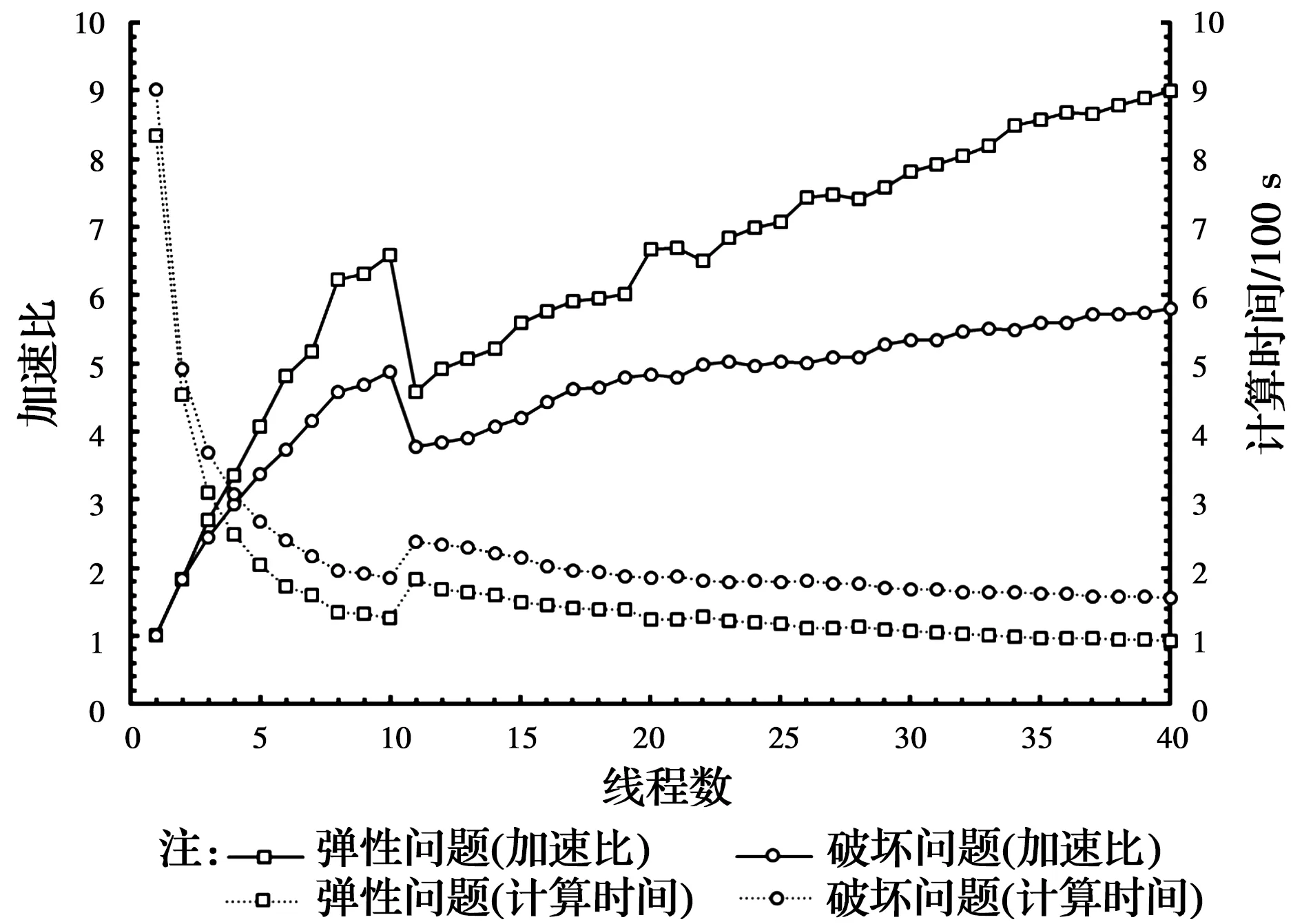
图9 工作站WS-2对于弹性模型和破坏模型的并行效率测试结果Fig.9 Parallel efficiency test results for elastic model and failure model of 4D-LSM on
1.7.2 计算规模的影响 由图7、图8可知,对于大小不同的模型,在相同条件下,其加速比有一定的区别。例如工作站WS-1使用40线程时,“Cube_50”“Cube_100”和“Cube_150”的加速比分别为9.1×、8.0×和10.8×,而相同情况下,工作站WS-2上对应的加速比分别为9.0×、8.2×和7.7×。若仅就这3种大小的模型而言,则工作站WS-1上“Cube_150”加速效果最好(10.8×),而工作站WS-2上“Cube_50”才是加速效果最好的(9.0×)。因此,模型的大小对加速效果有一定的影响,但这种影响没有普遍的规律,随计算机硬件配置的不同而不同。
同时也发现,弹性模型的计算时间与模型的规模呈正比,而破坏模型则并非如此。对于破坏模型而言,颗粒检索会消耗额外的时间,破坏的颗粒越多,每一步的计算时间就越长,但每一个破坏颗粒额外消耗多长时间还不明确,整个破坏过程目前也无法预测。由于这些“复杂性”,测试结果中破坏模型的计算时间与规模大小的关系曲线并不具有普适性,只能说明一般情况下是非线性的,从而区别于弹性模型的线性关系。
1.7.3 计算硬件的影响 CPU的主要参数包括频率、核心数量和线程数量等,更高的CPU频率、更多的核心或者线程都能够获得更快的计算速度。因此,由表1可知,一般情况下,拥有8线程3.6 GHz CPU的PC-1要比拥有4线程3.0 GHz CPU的PC-2更快,WS-1也会因为更高CPU的频率而获得比WS-2更好的性能。将图4中关于计算时间的数据做进一步处理后得到表2,表中ΔPC、ΔWS分别为PC-1与PC-2、WS-1与WS-2计算同一模型所用时间之差。从表2来看,虽然有几处Δ值为负数,但都是在模型较小、整个计算时间较短的情况下发生,不具有代表性,而绝大部分Δ值都为正数。因此,从统计的角度,对于同一个模型,可以认为PC-1比PC-2耗时更多,WS-1比WS-2耗时更多,也就是说,PC-2和WS-2计算速度更快,与之前的预测刚好相反,这说明4D-LSM的计算速度并非完全由CPU的性能决定。在表1中,对比4台计算机的硬件,PC-2和WS-2唯一的优势就是拥有更高的内存带宽。由于计算时间不仅包括CPU处理数据的时间,也包括其他必要的时间消耗,如CPU和内存交换数据的时间,高内存带宽意味着数据传输更快,最终的结果是PC-2和WS-2在计算时速度更快。因此,对于4D-LSM,若CPU性能差距不是很悬殊,则内存带宽成为计算速度非常重要的影响因素。
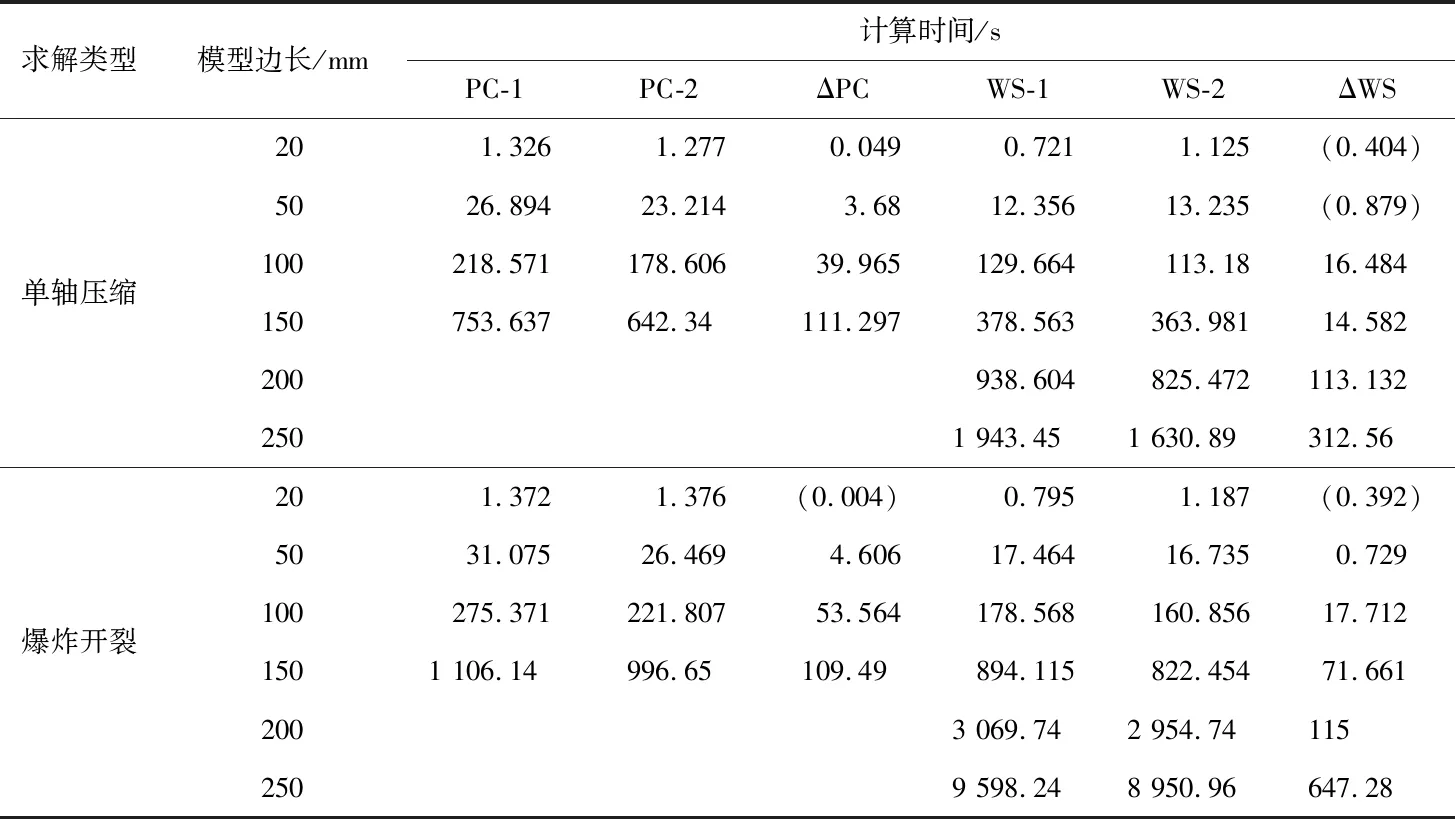
表2 使用最大线程数计算不同大小模型的时间消耗表Table 2 Calculating time of different size models using maximum thread number
1.7.4 并行计算量瓶颈分析 将两组模型(单轴压缩、爆炸开裂)按从小到大的顺序依次运行,记录其计算时间以及消耗的物理内存,测试时,每台计算机都使用最大线程,例如,PC-1使用8线程,而两台工作站WS-1、WS-2均使用40线程。从小到大的立方体模型的边长为20、50、100、150、200、250、300、350、400 mm等,在此序列下,PC-1、PC-2、WS-1、WS-2能计算的最大模型边长分别是150、150、250、300 mm,对应的颗粒数分别为337.5万、337.5万、1 562.5万和2 700万。由此可见,不论是弹性模型还是破坏模型,模型大小(颗粒数)与消耗的物理内存呈同一个线性关系。事实上,经过更进一步的数据分析发现,内存消耗与使用哪台计算机也没有联系,即模型的颗粒数量与内存消耗存在一一对应的关系(如图10所示),每100万颗粒约需要1.8 GB内存,目前来看,4D-LSM的计算量由计算机的内存容量决定。例如,WS-1的内存容量是32 GB,当计算边长为250 mm的模型时,4D-LSM消耗的内存约为28 GB,而下一个模型边长是300 mm,颗粒数量2 700万,按前述标准约需要48 GB的内存,因此,在WS-1上无法计算,最终,该模型在拥有64 GB内存的工作站WS-2上运行,而2 700万颗粒也几乎是WS-2的极限计算量。然而,对于阿里云来讲,则可以最大运行10亿单元的计算模型。从这点上来讲,云计算为一些对颗粒规模要求十分庞大的问题提供了除传统超级计算集群之外的可行解决途径。相比传统超级计算集群,云计算无需对代码进行修改,也无需进行昂贵的硬件投资。然而,4D-LSM是采用自建的图形交互界面建模,能够建立多大的模型受制于显存。例如,WS-2配备的“NVIDIA Quadro M5000”具有8 GB的显存,其构建的最大模型是450×450×450(约9 000万颗粒)。如果假设建模所需显存与颗粒数成正比,构建10亿颗粒的模型则至少需要大约88 GB的显存,因此,目前4D-LSM大规模并行的瓶颈在于前处理。
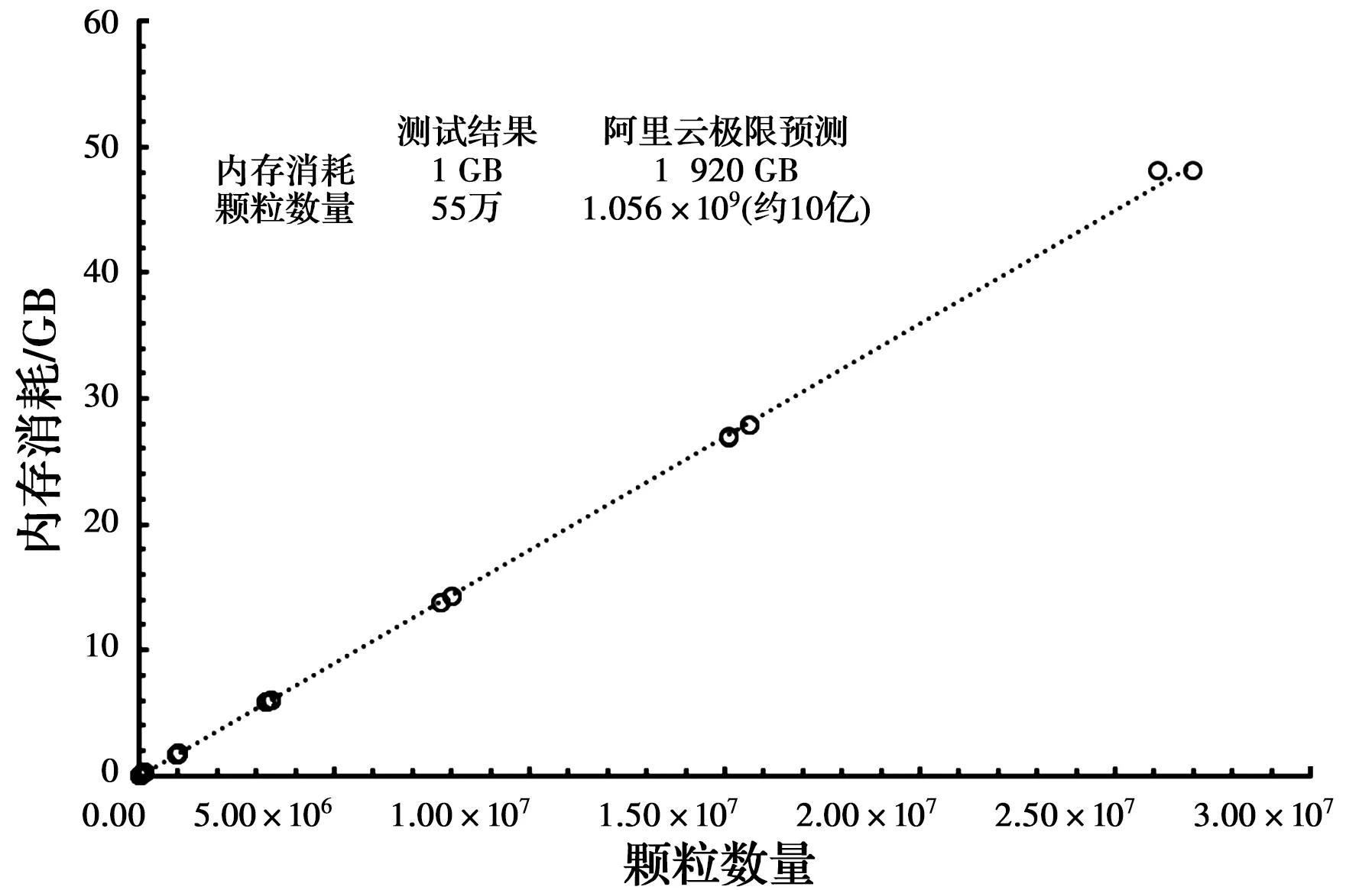
图10 模型大小与内存消耗的关系Fig.10 The relationship between model size and
2 应用案例
采用4D-LSM进行三维裂纹扩展分析。币型裂纹试样的尺寸及荷载条件如图11(a)所示,裂纹形状为圆形,直径18 mm,厚度1 mm,中心位置与整个立方体试样中心位置重合,裂纹面与试样底面夹角θ=30°。建立两个4D-LSM模型,一个解析度为110×110×110(约130万颗粒),另一个解析度为220×220×220(颗粒数大约为1 060万),除此之外,两个模型并无其他任何差别。图11给出了针对三维币形裂纹的计算模型,采用并行4D-LSM进行了求解。图12展示了三维币型裂纹模型在不同解析度下的裂纹发展过程。通过对比,低解析度模型虽然能大致展现裂纹的扩展过程,但裂纹形态相对比较粗糙,裂纹扩展的对称性远不如高解析度模型。由此可见,更高解析度的4D-LSM模型对精准模拟三维裂纹扩展问题非常关键。基于云计算的并行计算技术可以求解更高解析度的计算模型,非常适合于求解三维裂纹扩展的计算。
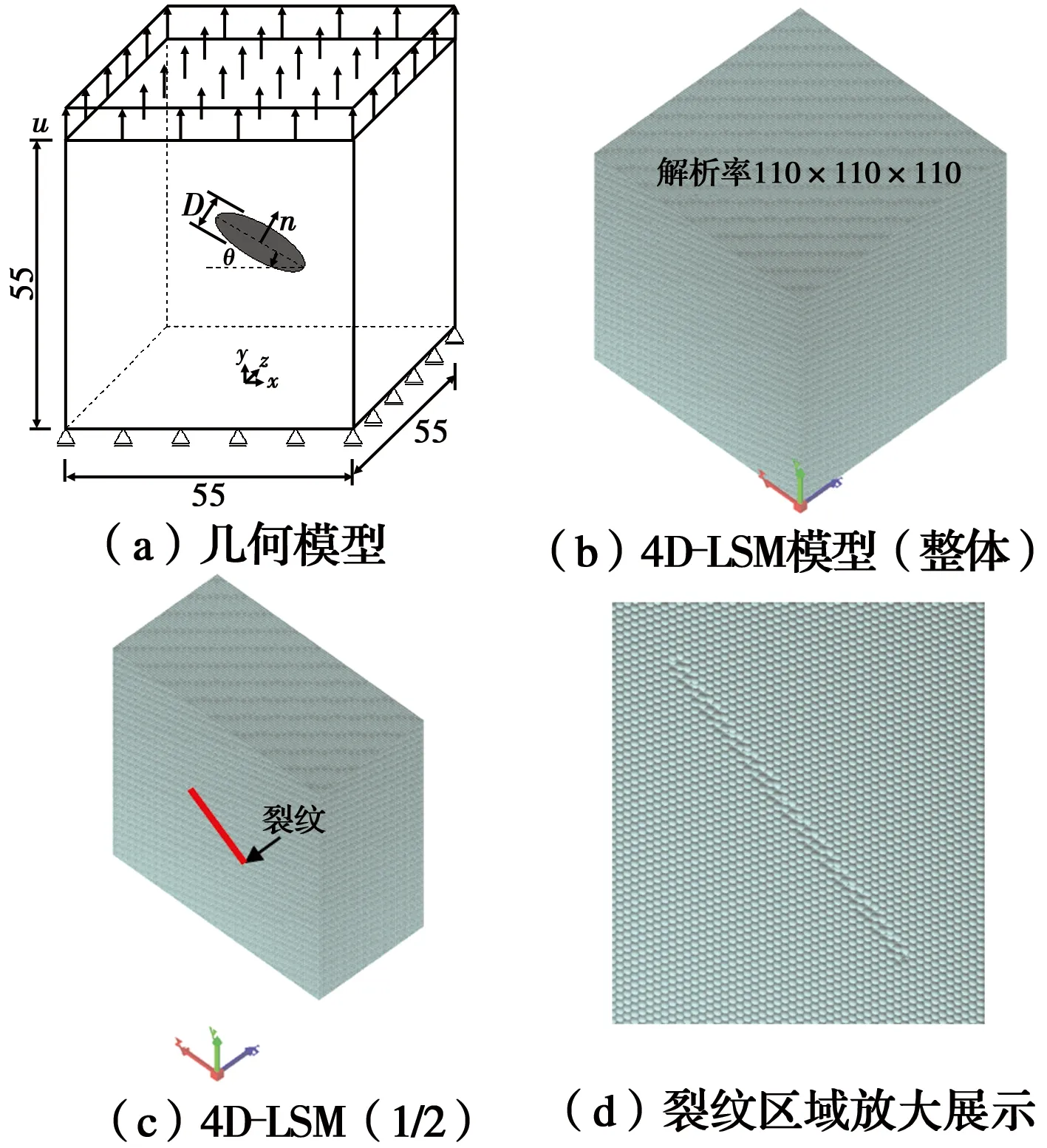
图11 三维币型裂纹扩展模型Fig.11 The model of three-dimensional
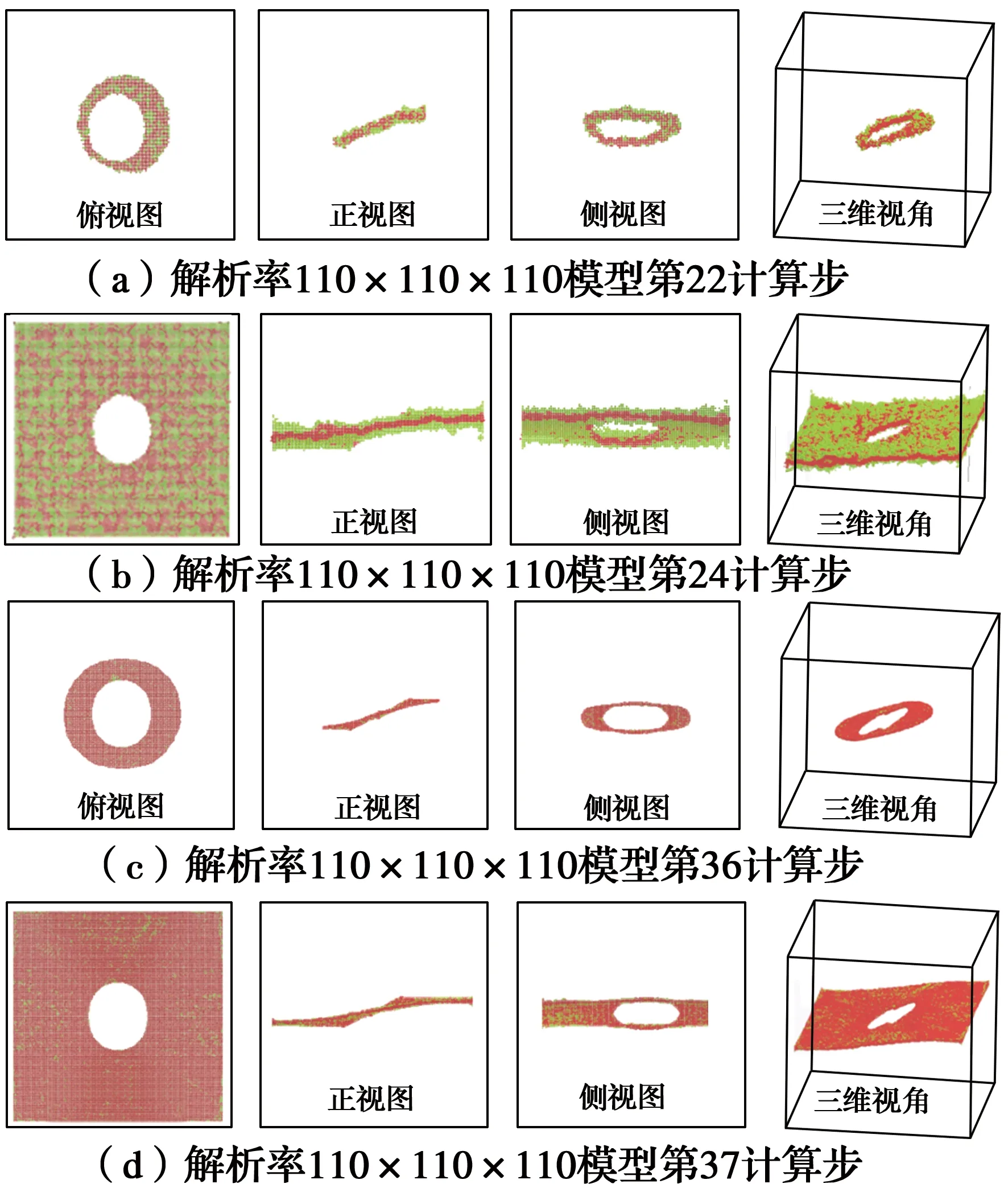
图12 裂纹扩展过程Fig.12 The crack propagation
3 结论
主要研究了4D-LSM在云计算环境下的并行性能,考虑了线程数量、硬件资源、模型大小、求解类型等因素。得到如下主要结论:
1)4D-LSM具有较好的并行性能,在20核的双路计算机上的最大加速比接近11.0×,而在64核的云服务器上的加速比接近17×。
2)4D-LSM模型的规模对加速效果有一定的影响,并因使用的计算机不同而不同。
3)4D-LSM求解弹性问题的加速效果优于求解破坏问题,使用的线程数量越多,这种差别表现得越明显。
4)非破坏模型的计算时间与颗粒数呈正比关系,而破坏模型由于其“复杂性”,通常情况下不是正比关系。
5)4D-LSM模型的颗粒数量与内存消耗呈正比,计算机的极限计算量由内存容量决定,每100万颗粒大约需要1.8 GB的内存,若要求解10亿颗粒的模型,理论上至少需要1.8 TB的内存。
6)对于双路计算机应当注意,当线程数量介于单颗CPU的物理核心数和双CPU的总物理核心数时,计算效率会下降,并且造成计算资源的浪费。
7)虽然云计算非常灵活且能提供强大的高性能计算能力,但其性价比也值得商榷,使用时应当综合考虑,有的放矢。
另外,需要说明:
1)在测试极限计算量时只考虑了物理内存,实际上有些4D-LSM模型在内存需求超过计算机的物理内存时也可以计算,比如边长为200 mm的单轴压缩模型,颗粒数量是800万,大约需要14.4 GB的内存,却可以在内存容量8 GB的PC-2上运行,这是因为系统自动启用了虚拟内存(此处虚拟内存是相对物理内存而言,并非编程模式下所指的虚拟地址空间),但此时计算速度非常缓慢,不在可接受的范围,因此,未予以考虑。
2)对于双路计算机,当使用的线程数量介于单颗CPU核心数和双CPU总核心数时,不仅计算效率会下降,而且多次重复计算的结果表明:在此区间计算时间的离散程度也急剧增加,即计算效率不稳定,计算效率不稳定的情况与求解类型无关。相差40%的结论是因为统计了WS-2在10线程和20线程之间重复计算100次同一个模型的计算时间,求出了计算时间的变异系数,该变异系数最高为20%左右。因此,当线程数量处于该区间时,同样模型的两次计算时间有可能相差40%。
3)对于本地计算机,当使用的线程数量超出计算机的最大线程数时,其计算效率会下降20%左右,但对于云计算的虚拟服务器而言,超出最大线程后,计算效率并不会下降,而是保持在同一水平线上。
