质点和刚体碰撞时的恢复系数30届全国物理竞赛复赛第2题说起——从第

(杭州市萧山区第五高级中学 浙江 杭州 311202)

黄 晶

(杭州学军中学 浙江 杭州 312000)

汪 飞

(江苏省海门中学 江苏 南通 226100)

1 细致思考 提出问题

【例1】(第30届全国中学生物理竞赛复赛第2题)一长为2l的轻质刚性细杆位于水平的光滑桌面上，杆的两端分别固定一质量为m的小物块D和一质量为αm(α为常数)的小物块B，杆可绕通过小物块B所在端的竖直固定转轴无摩擦地转动.一质量为m的小环C套在细杆上(C与杆密接)，可沿杆滑动，环C与杆之间的摩擦可忽略.一轻质弹簧原长为l，劲度系数为k，两端分别与小环C和物块B相连.

一质量为m的小滑块A在桌面上以垂直于杆的速度飞向物块D，并与之发生完全弹性正碰，碰撞时间极短. 碰撞时滑块C恰好静止在距轴为r(r>l)处.

(1)若碰前滑块A的速度为v0，求碰撞过程中轴受到的作用力的冲量；

(2)若碰后物块D,C和杆刚好做匀速转动，求碰前滑块A的速度v0应满足的条件.

第(1)问参考解答(部分)：

由于碰撞时间Δt很小，弹簧来不及伸缩碰撞已结束. 设碰后A,C,D的速度分别为vA,vC,vD，显然有

(1)

以A,B,C,D为系统，在碰撞过程中，系统相对于轴不受外力矩作用，其相对于轴的角动量守恒

mvD2l+mvCr+mvA2l=mv02l

(2)

由于轴对系统的作用力不做功，系统内仅有弹力起作用，所以系统机械能守恒. 又由于碰撞时间Δt很小，弹簧来不及伸缩碰撞已结束，所以不必考虑弹性势能的变化. 故

(3)

由式(1)、(2)、(3) 解得

(4)

[可利用弹性碰撞特点v0=vD-vA代替式(3) ，同样可解出式(4)]

……(略)

问题由来：上述试题解答过程本身并不存在错误，不过其中最后一点补充说明让人心生狐疑，其说道,可利用弹性碰撞特点v0=vD-vA代替式(3)，即能量守恒一式，让人产生疑问的缘由在于式(3)利用了完全弹性碰撞过程中接近速度与分离速度相等这一特性，即恢复系数e=1.恢复系数的概念建立在质点与质点碰撞的过程之上[1]，而在该题中，其物理过程属于质点与刚体的碰撞，恢复系数的概念在其中是否同样适用，很多教材中并没有给出相关的说明.

由于上述疑问，笔者认为有必要通过分析将恢复系数的概念从质点与质点的碰撞拓展到质点与刚体相碰的过程中，以消除疑虑.

2 建立模型 消除疑惑

如图1所示，一小球与杆发生完全弹性正碰，已知小球质量为m，杆质量为M，杆相对质心的转动惯量为J，碰撞前，小球速度为v，杆质心的速度为vC，杆角速度为ω，碰撞点O距杆的质心距离为r，设碰撞之后，小球速度为v′，杆质心的速度为vC′，杆角速度为ω′，碰撞过程中小球与杆之间冲量大小为I.

图1 小球与杆发生弹性正碰

对小球分析，由动量定理

-I=mv′-mv

(5)

对杆分析，由质心运动定理

I=MvC′-MvC

(6)

由冲量矩定理

Ir=Jω′-Jω

(7)

对系统分析，碰撞前后能量守恒

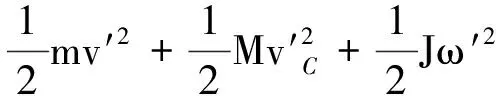
(8)

由式(5)、(6)、(7)可得

再将结果代入式(8)中整理得到

(9)

同理可得

(10)

注意到vC+ωr为杆上碰撞点对地速度，故

v-vC-ωr=v-(vC+ωr)

为碰撞前的小球与杆上碰撞位置的接近速度

为碰撞后杆与小球的分离速度，由式(9)和式(10)得到

即小球与杆碰撞前后接近速度等于分离速度，与质点之间完全弹性碰撞结论一致[2].

上述分析过程与杆质量分布、形状、碰撞位置均无关，故可将这一分析推广到更为一般的质点与刚体的碰撞过程中，对于质点与刚体的完全弹性碰撞过程，利用已知的守恒定律及其他条件完全可以得到结论，碰撞前后接近速度等于分离速度这一条件并非独立方程，故上述分析的意义在于在实际计算过程中，可利用这一条件替换能量守恒方程，从而起到简化计算的作用.

3 小试牛刀 归纳总结

【例2】(第23届全国中学生物理竞赛复赛第2题)如图2所示，一根质量可以忽略的细杆，长为2l，两端和中心处分别固连着质量为m的小球B,D和C，开始时静止在光滑的水平桌面上.桌面上另有一质量为M的小球A，以一给定速度v0沿垂直于杆DB的方间与右端小球B作弹性碰撞.求刚碰后小球A,B,C,D的速度，并详细讨论以后可能发生的运动情况.

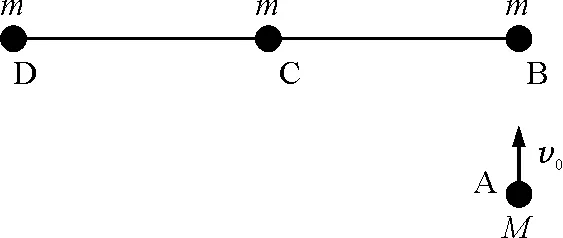
图2 例2题图

参考答案提供解答(部分)：

设刚碰撞后，小球A,B,C,D的速度分别为vA,vB,vC,vD，并设它们的方向都与v0的方向相同．由于小球C位于由B,C,D这3个球组成的系统的质心处，所以小球C的速度也就是这系统质心的速度．因碰撞前后4个小球组成的质点组的动量守恒， 故有

Mv0=MvA+3mvC

(11)

碰撞前后质点组的角动量守恒，有

0=mlvC+2mlvD

(12)

这里角动量的参考点设在与B球重合的空间固定点，且规定顺时针方向的角动量为正．因为是弹性碰撞，碰撞前后质点组的动能相等，有

(13)

因为杆是刚性杆，小球B和D相对于小球C的速度大小必相等，方向应相反，所以有

vB-vC=vC-vD

(14)

解式(11)～(14)，可得两个解

vC=0

(15)

和

(16)

因为vC也是刚碰撞后由B,C,D这3个小球组成的系统质心的速度，根据质心运动定律，碰撞后这系统的质心不可能静止不动，故式(15)不合理，应舍去．取式(16)时可解得刚碰撞后A,B,D这3个球的速度

以下基于恢复系数的角度进行分析.

碰撞前后系统动量守恒

Mv0=MvA+3mvC

(17)

系统碰撞前后基于C点角动量守恒

Mlv0=2ml2ω+MlvA

(18)

其中ω为碰撞后杆的角速度.

接近速度等于分离速度

v0=(vC+ωl)-vA

(19)

再考虑到

vB=vC+ωl

(20)

vD=vC-ωl

(21)

联立同样可以得到结果.

质点与刚体完全弹性碰撞的问题在物理竞赛中时有涉及，利用常规的动量、能量以及角动量守恒，可以得到结果，然而,由于能量守恒为二次方程，联立方程计算较为复杂，而如果引入恢复系数，将能量守恒方程用接近速度等于分离速度这一方程替换，可以减少大量的计算量，为考试赢得时间，这也为相关习题的解答提供了新的思路和新的启发.