一类亚纯函数的Fekete-Szeg不等式
2019-06-21李宗涛付小娟
李宗涛,付小娟
(广州民航职业技术学院 数学教学部,广东 广州 510403)

S*(β)表示Σ中满足-Re{zf′(z)/f(z)}>β(0≤β<1)的全体函数类,C*(β)表示Σ中满足-Re{1+zf′(z)/f′(z)}>β(0≤β<1)的全体函数类,S*(β)和C*(β)就是我们说的β级亚纯星象函数类与β级亚纯凸象函数类.
设φ(z)是U={z∈ℂ:|z|<1}内具有正实部且满足φ(0)=1,φ′(0)>0的解析函数,它把区域U映照到一个关于实轴对称且关于1星型的像域上,其泰勒展开式具有下述形式:

令Σ*(φ)表示满足下列条件的函数类:Σ*(φ)={f∈Σ:-zf′(z)/f(z)≺φ(z)},此函数类是由Silverman等[1]引入的.很明显,(0≤β<1)时,Σ*(φ)=S*(β).
2013年,Aouf[2]研究了亚纯函数类的Fekete-Szeg不等式.Mocanu[3]定义了α-凸函数类,其函数满足它是一个从星象函数向凸函数过渡的函数.后来Miller[4]证明了:当α<1时,f(z)∈S*(0);当α≥1时,f(z)∈K(0).仿照亚纯函数类(φ),我们定义了如下函数类.
定义1设φ(z)是U内具有正实部且满足φ(0)=1,φ′(0)>0的解析函数,它把区域U映照到一个关于实轴对称且关于1星型的像域上.令,如果f(z)∈Σ,满足φ(z),则称函数
我们注意到:选择合适的参数λ,φ(z),可以得到下面的函数类:
为得到结论,需要下面的引理:
引理1[9]设在U内解析,且Rep(z)>0,则|pn|≤2,(n≥1).
引理2[10]如果是U内具有正实部的解析函数,则对任意的t∈ℂ,有2max{1,|2t-1|},等号在函数或时成立.
引理3[11]如果是U内具有正实部的解析函数,则对任意的t∈ℝ,有t<0或t>1时,等号成立当且仅当或是它的一个旋转;当0<t<1时,等号成立当且仅当或是它的一个旋转;当t=0时,等号成立当且仅当或是它的一个旋转;当t=1时,等号成立当且仅当p(z)是t=0的情况下等号成立时的任意一个函数的逆.同时,当0<t<1时,不等式可以改进为:
1 主要结果
定理1如果f(z)由式(1)给出,且则和
证明因为所以存在U内的施瓦兹函数u(z)(u(0)=0,|u(z)|<1),满足
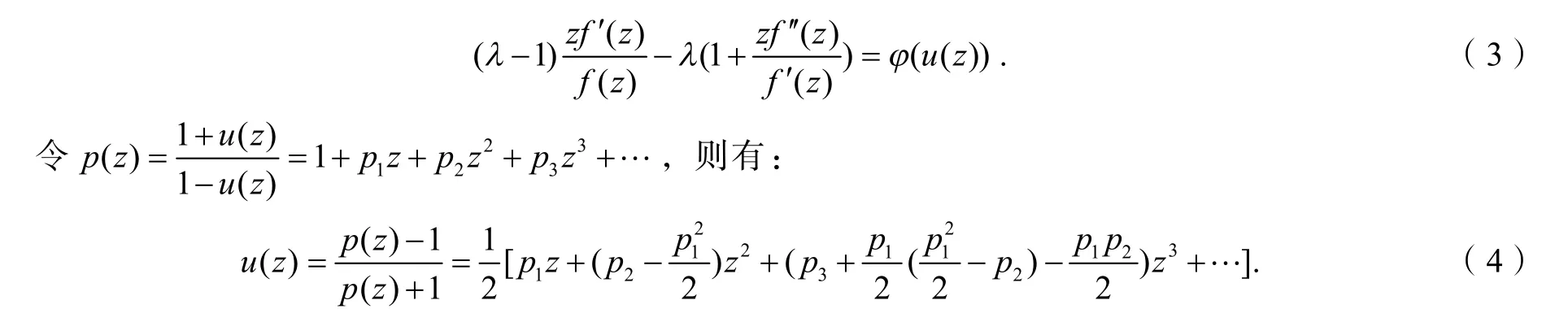
由式(3)、(4)得
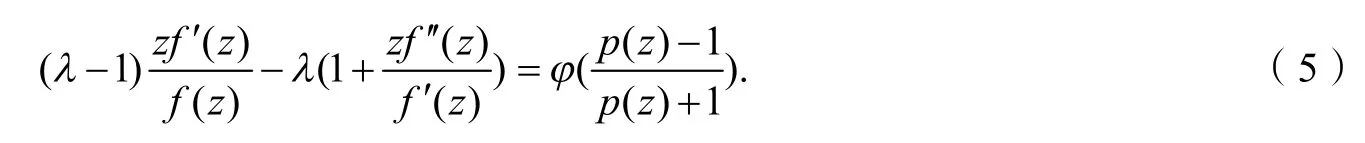
由式(2)、(4)得
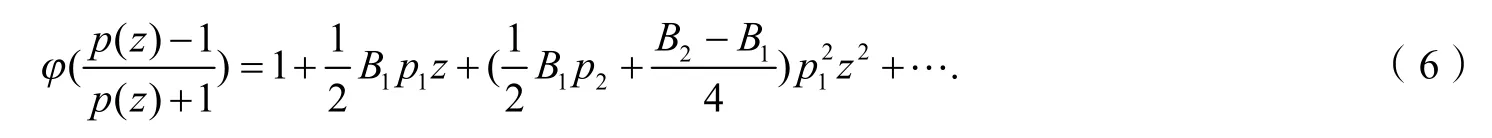
比较式(5)、(6)中z和2z的系数,得
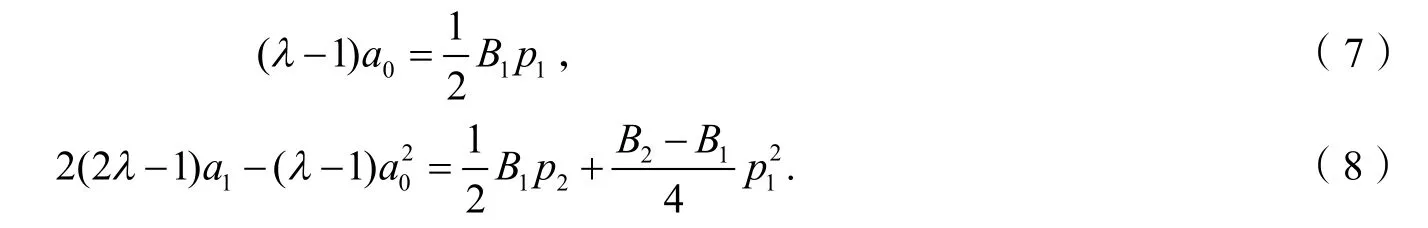
由式(7)得

由式(8)、(9),得
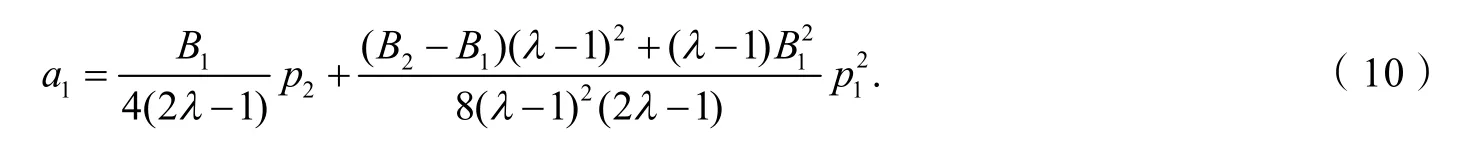
由式(9)及引理1,得
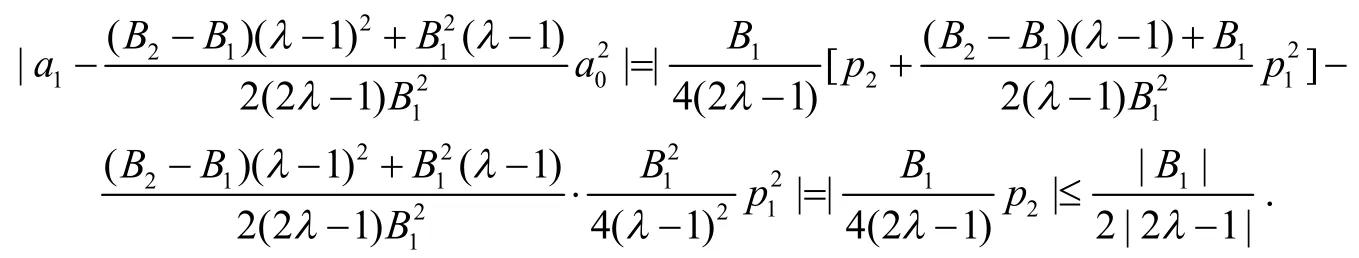
定理2如果f(z)由式(1)给出,并且,则对任意的μ∈ℂ,当B1≠0时,有,且对所有的μ等号都是成立的.
证明由式(9)和(10),得
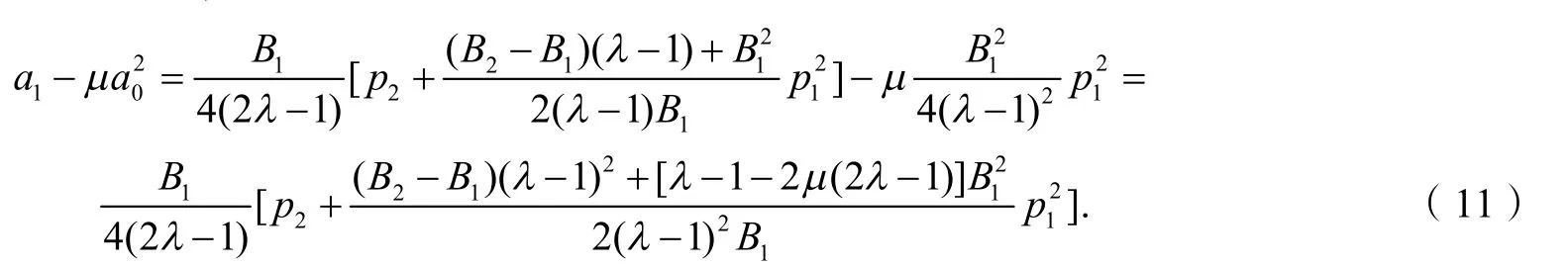
当f(z)取U中满足的函数时,等号成立.
下面讨论μ∈ℝ的情况.
定理3设φ(z)=1+B1z+B2z2+B3z3+…(B1>0)满足定义1中的条件.如果f(z)由式(1)给出,并且则对任意的μ∈ℝ,有
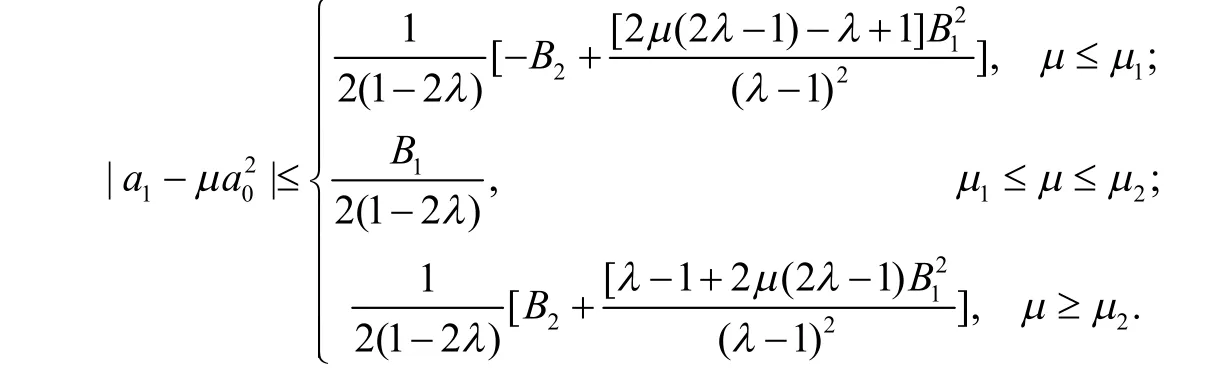
证明由式(11)及引理3,得
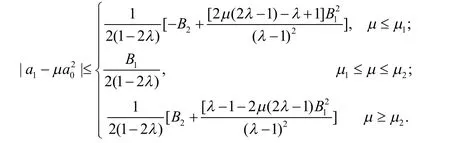
为了证明上面的界是精确的,我们记函数(n=2,3,…)为方程组的一个解.并且记函数和(λ≥0)分别为方程组和的一个解.易知函数.简记由引理3,当μ<μ1或μ>μ2时,等号成立当且仅当f是或是它的一个旋转;当μ1<μ<μ2时,等号成立当且仅当f是或是它的一个旋转;当μ=μ1时,等号成立当且仅当f是或是它的一个旋转;当μ=μ2时,等号成立当且仅当f是或是它的一个旋转.
若μ1≤μ≤μ2,根据引理3,定理3可以被改进为:
定理4设φ(z)=1+B1z+B2z2+B3z3+…(B1>0)满足定义1中的条件,μ1和μ2由定理3给出,且则有
注:通过选择适当的参数,我们得到了前面提到的几个函数类的Fekete-Szeg不等式.
2 在Hadamard卷积定义的函数类上的应用
令f(z),g(z)∈Σ,其中f(z)由式(1)定义,Hadamard积(或卷积)f*g定义为类似于前面定理的证明,有如下结论成立.
定理5设f(z)∈Σ由式(1)给出,如果则有和
定理6如果f(z)由式(1)给出,,并且则对任意的μ∈ℂ,当B1≠0时,有且对所有的μ等号都是成立的.
定理7设φ(z)=1+B1z+B2z2+B3z3+…(B1>0)满足定义1中的条件. 如果f(z)由式(1)给出,并且则对任意的μ∈ℝ,有其中且对所有的μ等号都是成立的.
定理8设φ(z)=1+B1z+B2z2+B3z3+…(B1>0)满足定义1中的条件,μ1和μ2由定理7给出,且如果f(z)由式(1)给出,则有
注:在定理5~8中,令则定理5~8即为定理1~4.
3 推论
Pochhammer定义符号(u)n:
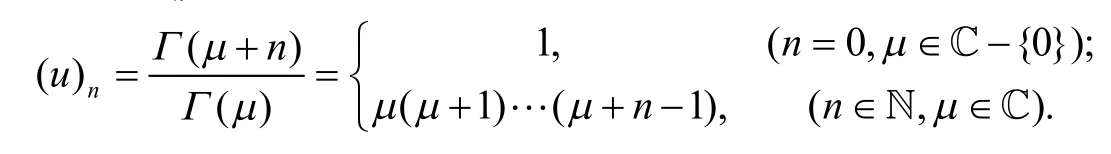
对于复参数a,b,c且c≠0,-1,-2,-3,…,Gaussian定义超几何函数2F1(a,b,c;z):
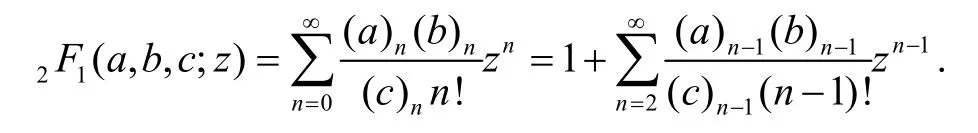
利用Hadamard卷积和Gaussian超几何函数,Hohlov[12-13]定义并研究了Hohlov算子Ia,b,cf(z)=其中
推论1如果f(z)∈Σ由式(1)给出,并且则有和
推论2设φ(z)=1+B1z+B2z2+B3z3+…(B1>0)满足定义1中的条件.如果f(z)由式(1)给出,并且则对任意的μ∈ℂ,当B1≠0,a≠0,b≠0时,有
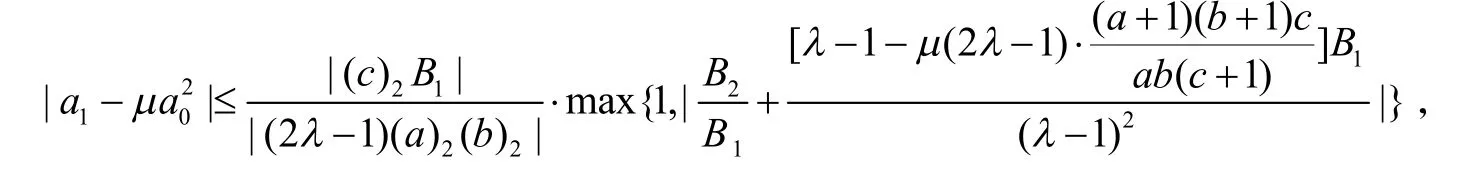
且对所有的μ等号都是成立的.
推论3设φ(z)=1+B1z+B2z2+B3z3+…(B1>0)满足定义1中的条件.如果f(z)由式(1)给出,并且则对任意的μ∈ℝ,当a>0,b>0时,有
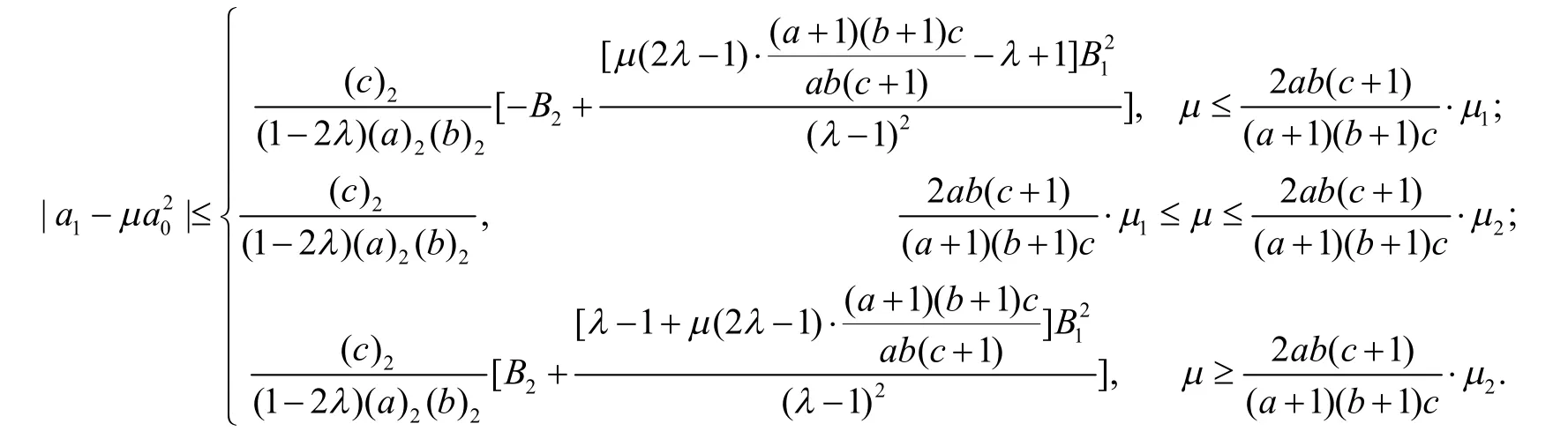
推论4设φ(z)=1+B1z+B2z2+B3z3+…(B1>0)满足定义1中的条件,μ1和μ2由推论3给出,且如果f(z)由式(1)给出,并且则对任意的μ∈ℝ,当a>0,b>0时,有和
