岩体加固抗爆炸性能*

2019-06-21徐干成袁伟泽顾金才张向阳

爆炸与冲击 2019年5期

徐干成，袁伟泽，顾金才，张向阳

（1.空军研究院工程设计研究所，北京 100068；2.军事科学院工程兵防护工程研究所，河南洛阳 471023）

地下防护工程具有隐蔽性强、抗毁性高、封闭性好等优点。然而，对于防护层较薄的已建、或必须在不具备深防护层条件的地方构筑地下防护工程，为了抵抗钻地弹的爆炸破坏能力，通常采用高强混凝土结构或对混凝土衬砌结构采取加固措施来增强地下防护工程的抗震塌能力[1-2]；同时，还可以对岩体进行加固，提高围岩抗力，从而提高地下工程的整体抗力等级。锚索技术广泛应用于岩土工程中，对静载条件下锚索性能的研究已较成熟，而对爆炸荷载下锚索的计算方法、优化设计方法以及抗爆机理等方面还存在较多问题[3]。为研究锚索及被加固岩体在爆炸载作用下的破坏机理，已进行了大量喷锚支护爆炸实验，研究的重点是从内部对洞室进行加固后洞室的动态反应及破坏特点，而对原岩及被加固原岩抗爆性能的研究仍不够深入[4-9]。为此，本文中提出采用交叉锚索对岩体进行外加固的方法，并展开一系列抗侵彻、爆炸实验研究[10-13]；在此基础上，采用模型实验和数值计算的方法对爆炸造成加固岩体的破坏，包括爆腔尺寸、压碎区范围等进行研究，比较采用不同锚索参数（锚索角度、锚索间距）对加固岩体抗爆效果的影响。

1 模型实验设计与内容

1.1 模型相似比

爆炸实验模型要与实际原型在几何、物理及边界条件上保持相似。当模型实验的重力场与原型相同时，依据Froude 相似关系，模型材料应满足的基本相似关系为：

式中：Kσ、Kρ、KL分别为模型与原型之间应力、密度、几何尺寸的量纲相似比。根据现有模型实验装置条件、模拟材性实验结果以及课题组已开展的侵爆实验等[12-13]，确定本次实验几何比尺KL=0.095，密度比尺Kρ=0.72，根据公式（1）可知：Kσ=0.068，集中力比尺KP=0.000 61，质量比尺Km=KρKL3=0.000 61，能量相似比尺KE=KσKL3=0.000 058。

1.2 模型材料选择

（1）炸药。选取美国GBU-28/B 钻地弹原型弹体，其装药量为306×1.35=413.1 kg TNT 当量。模拟实验中使用的炸药为块状TNT，其密度为1 600 kg/m3。

（2）模拟岩体材料。实验选取中等强度的Ⅲ级岩体作为原型岩体，参照文献[13]确定本次实验的模拟材料为水泥砂浆，其质量配比为：水泥∶砂∶水=1∶10∶1.1，原岩及模拟材料的力学参数抗压强度Rc、抗拉强度Rt、黏聚力C、内摩擦角φ、变形模量Em、泊松比μ、密度ρ 见表1。

表 1 原岩与选定模拟材料物理力学参数Table 1 Mechanics parameters of the rock and selected material

(3）模拟锚索。原型锚索为一个孔内设3 束规格为7× ∅5 mm 标准钢绞线，模拟锚索采用3 根直径为1.5 mm 的纯铝丝机械绞制而成，钢绞线与选定铝绞线的力学性能等相关参数公称截面面积A、直径R 等见表2。

表 2 钢绞线与选定铝绞线力学参数Table 2 The mechanics parameters of cable and selected aluminium stranded wire

1.3 模型尺寸确定及制作

实验时在模型体表面钻凿的竖直向下的送药孔直径为60 mm，药包的高度为55 mm。实验爆炸装置的宽度为1.5 m（药孔直径的25 倍），装置的长度为2.4 m（药孔直径的40 倍），可满足介质边界条件。装置的高度为2.3 m（含下部消波坑），药包埋置深度为自顶面下1.2 m，远大于完全填塞深度，完全满足对完全填塞爆炸效果进行模拟的要求。实验装置及模型体大小如图1 所示。

模拟实验装置底部铺一层模型材料，夯实后为50 mm。共夯实四层，厚度为200 mm。当夯筑深度达到500 mm 时，将四个侧限装置闭合，然后再夯筑模拟岩体。在200 mm 层面上放好模拟锚索。每层锚索均倾斜45°，每相邻上下层锚索相互垂直，模拟岩体内锚索的定位如图2 所示。锚索体积占模拟岩体总体积的0.097%。

1.4 模拟岩体内传感器布置

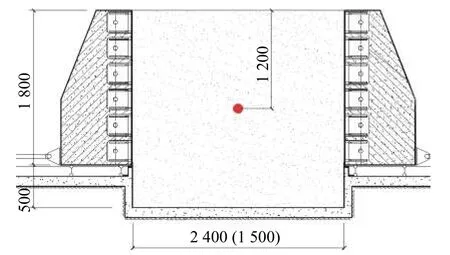
图 1 爆炸装置及模型体简图（单位：mm）Fig.1 Explosive device and model scheme (unit: mm)

图 2 模拟岩体内锚索的定位Fig.2 Anchor cable orientation in simulated rock

在爆炸模拟岩体中布置了应变测点和压力测点，即在距离模型顶面下1.2 m 高度上要设置应变和压力测点，以确定爆炸破坏半径（范围），测点与爆点在同一个水平面上。应变测试采用应变砖预埋法，压力测试采用在制作模型过程中把压力测试元件设在预定位置。测试装置测点布置如图3 所示，应变砖及PVDF 压力传感器如图4 所示。

2 实验结果分析

在配制模型材料时掺加有早强剂，15 d 后材料强度稳定且不再增加，故实验模型体硬化15 d 后进行抗爆实验。为了充分利用抗爆模型体，在一块模型体内进行多次爆炸实验，每次实验时爆点位置不变。为防止损坏实验装置未加固模型的药量依次为100、150、200 g，而加固模型的药量依次为100、150、200、250 g。爆炸实验完成后，对模型进行解剖，观察爆坑形状并测量爆坑尺寸。

2.1 爆炸测试曲线汇总分析

每次爆炸实验后对测得的多组应力、应变曲线进行整理，得到各个测点的峰值。为了使测点峰值具有通用性、可比性，对横、纵坐标进行无量纲处理，以未加固模型药量为100 g 实验结果为例。通过数据拟合得到测点压应力峰值、径向应变峰值和环向应变峰值分别与距爆心的比例距离的拟合曲线如图5所示，负幂函数关系式为：

图 4 测试用传感器Fig.4 Sensors for the experiments

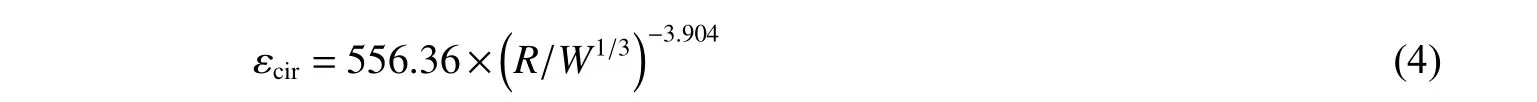
式中：R 为距爆点的距离，m；W 为药量，kg；P 为压力峰值、Rc单轴抗压强，MPa；ε 为应变峰值，10-6。

针对不同的爆炸药量，相同的比例距离有不同的测量值。根据爆炸相似原理，在相同的介质中、相同的比例距离具有相同的爆炸应力峰值及应变峰值等爆炸波参数。由于模拟岩体南、北方向较大，受边界影响较小。因此，以布置在北侧压力测点测得的数据和南侧应变测点测得的数据对其他数据及曲线进行归一化，如图6～8 所示。

图 5 未加固模型药量为100 g 实验结果Fig.5 Test results of unreinforcement under 100 g explosive load

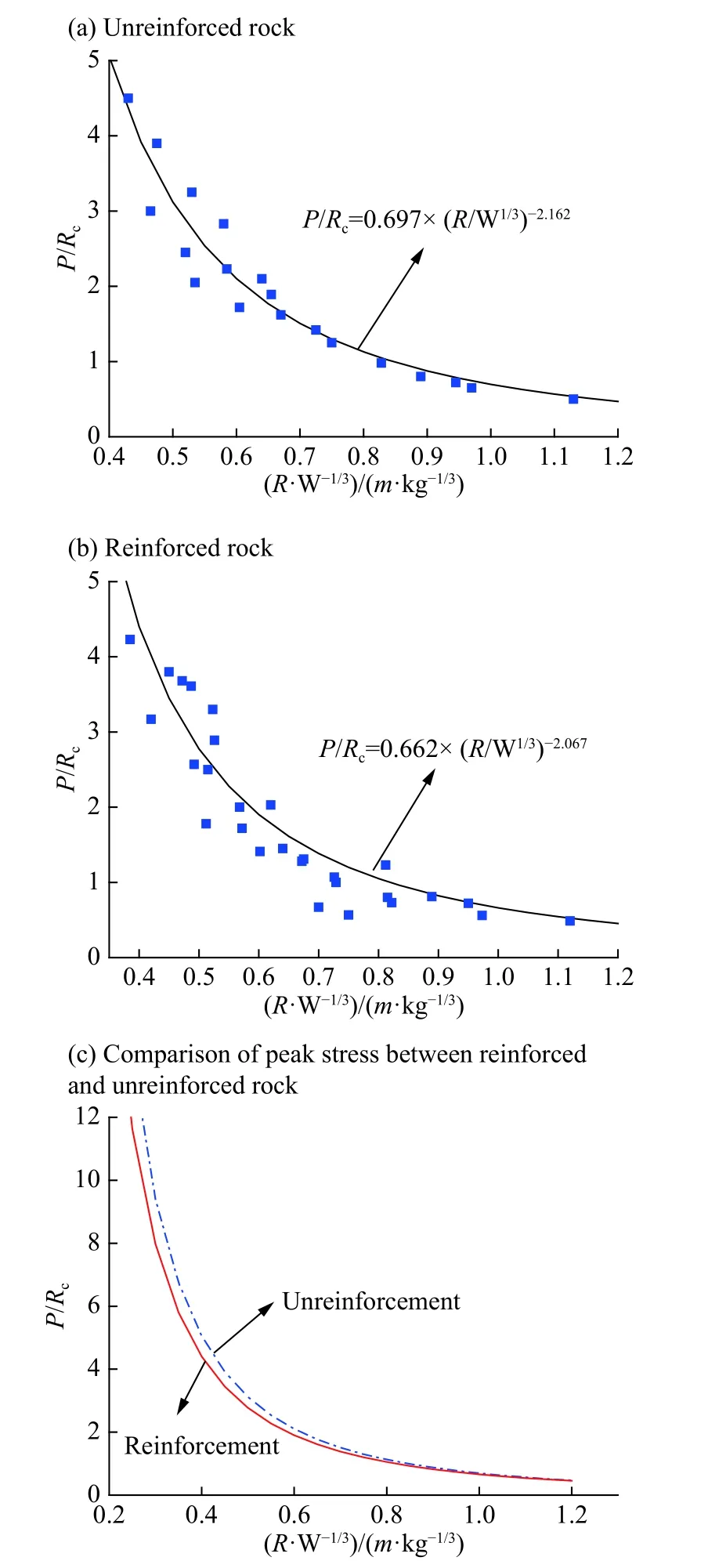
图 6 爆炸应力峰值与比例距离的关系曲线Fig.6 Peak stress-proportion distance curves of explosion

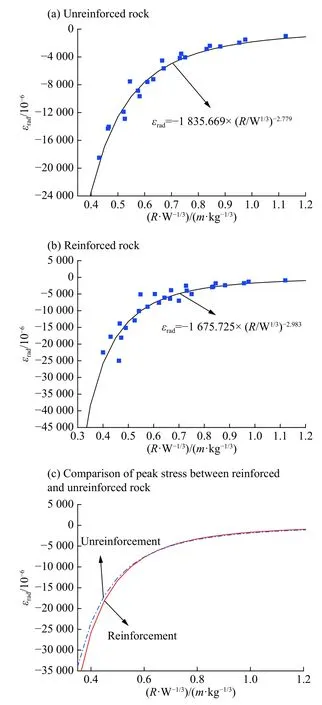
图 7 径向应变峰值与比例距离的关系曲线Fig.7 Radial peak strain-proportion distance curve of explosion

图 8 环向应变峰值与比例距离的关系曲线Fig.8 Toroidal peak strain-proportion distance curve of explosion

由6～8 图可知：（1）爆炸压力峰值、径向应变峰值和环向应变峰值与比例距离均呈负幂函数关系，且对应曲线形状相似；（2）在相同的比例条件下，无加固模拟岩体内的爆炸压应力峰值要大于对应的加固模拟岩体内的爆炸压应力峰值，且当比例距离小于1.1 时，两者之间越来越离散；（3）当比例距离小于0.5 左右时，无加固模拟岩体内的径向应变峰值绝对值要小于对应的加固模拟岩体内的径向应变峰值绝对值；当比例距离大于0.5 左右时，无加固模拟岩体内的径向应变峰值绝对值稍大于对应的加固模拟岩体内的径向应变峰值绝对值；（4）当比例距离大于1.1 时，两条环向应变曲线基本上重合在一起；当比例距离小于1.1 时，环向应变峰值曲线逐渐分散，在相同的比例距离条件下，无加固模拟岩体内的环向应变峰值要大于加固模拟岩体内对应的环向应变峰值。

加固试件材性实验表明，在模型材料内设置模拟锚索的铝绞线，其抗压强度和变形模量并不会得到显著提高，因此，加固后模型体的波阻抗也不会得到明显提高，这可能与设置的铝绞线数量较少有关，还不足以从根本上影响模型体的材性性质。当比例距离较大时，传播至测点处的爆炸压力波较小，铝绞线的变形较小，抗拉变形能力高的优点没有发挥出来，测得的应变和应力波峰值与未加固模型体内测得的基本相同。当比例距离较小时，铝绞线的发挥了其抗拉变形能力高的优点，约束限制住了其周边模型材料的变形，测得的应变比未加固模型体内同位置应变要小，这会直接造成测得的爆炸压力峰值小，此外，铝绞线变形消耗的爆炸能量也大，这也是造成在加固模型体内测得的爆炸压力峰值较小的原因。

2.2 模拟岩体解剖

爆炸完成后，进行爆炸模型体的解剖，暴露出爆腔，如图9 所示。

经测量，无加固模型爆腔最宽处宽250 mm，上下高度为260 mm；有加固模型爆腔最宽处290 mm，上下高度为230 mm。爆腔素描如图10 所示。

图 9 模型爆腔对比Fig.9 Explosion cavity comparison for the two models

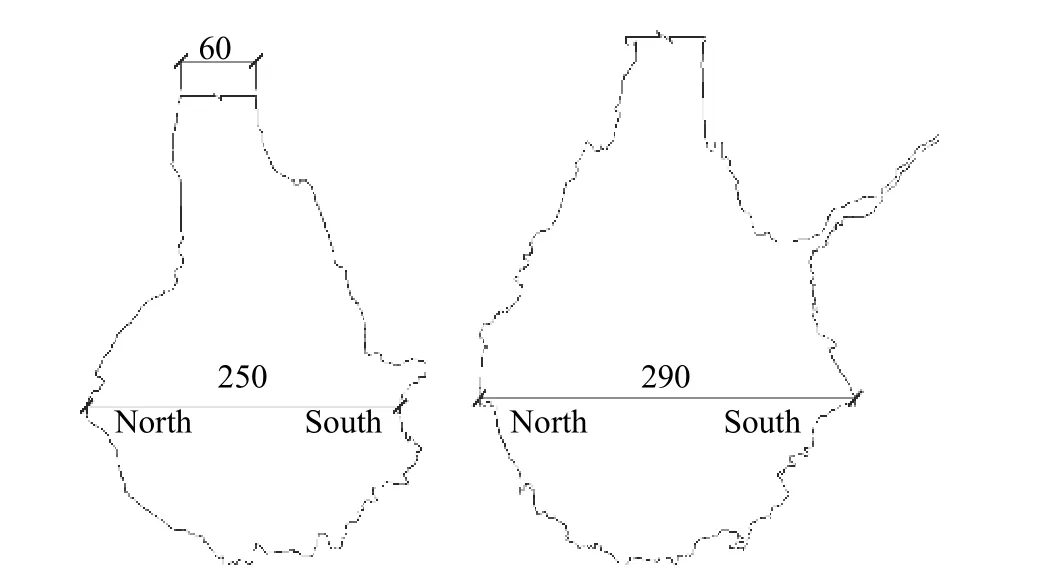
图 10 模型体爆腔素描图（单位：mm）Fig.10 Explosion cavity comparison of test models (unit: mm)

由图10 可知：在集团装药条件下，岩体内的爆腔不是呈球形而是呈上细下粗的花瓶形；由于无加固和加固模拟岩体的爆腔分别是在200、250 g 药量爆炸情况下形成的，加固模拟岩体的爆腔要比无加固模拟岩体的爆腔大，但无加固模拟岩体的爆腔高度较大。

3 数值模拟计算

3.1 数值模型简介及对比验证

采用LS-DYNA 进行数值模拟。模型中药包尺寸为长×宽×高=50 mm×2.50 mm×50 mm，模型尺寸相对于炸药尺寸大较多，模型边界条件为位移约束条件。计算中炸药与介质接触部分网格需要划分得较密，最小网格大小为炸药尺度的1/10；高能炸药爆轰产物的单元压力p 由状态方程求得，相关参数取值如下：A=741 GPa，B=18 GPa，ω=0.35，R1=5.56，R2=5.56，E=3.6 GJ/m3。由于模型的对称性，取1/4 模型计算，划分的有限元模型如图11 所示。

锚索加固体简化成8 节点显式结构实体单元，采用了莫尔-库仑模型，并根据实验数据定义体积应变与压力的关系曲线。材料在达到破坏后，黏聚力取为零，而内摩擦角保持不变，材料参数见表3。

首先对加固模拟岩体在药量为250 g 时的爆炸过程进行模拟，从而验证数值模型的可靠性。计算结果如图12～13 所示。由图12～13 可以看出：介质压缩区呈圆形，压缩半径约为250 mm；加固实验爆腔水平宽度290 mm、上下宽230 mm，均值260 mm；数值计算中距离爆心3 600 mm 处的介质应力为5.17 MPa，与抗爆实验测点5 测得的介质应力5.54 MPa 较为接近。基于上述分析可见数值模型对抗爆实验模拟较好。

图 11 数值模型网格划分Fig.11 Mesh partition of numerical model

表 3 数值模型参数Table 3 Parameters of numerical model

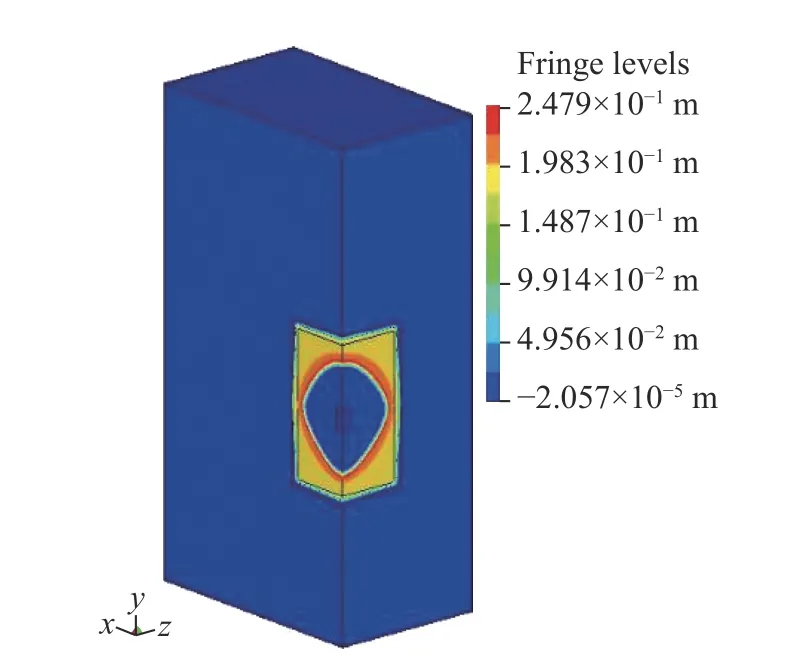
图 12 岩体内爆炸压缩区域图Fig.12 Explosion compression region in rock mass

图 13 岩体内应力云图Fig.13 Stress nephogram in rock mass

3.2 钢绞线角度变化对压缩半径的影响分析

在爆炸药量均为250 g 的情况下，分别计算交叉锚索角度Cm、锚索布置密度ρm对压缩半径Ry的影响，计算方案及结果如表4 所示。

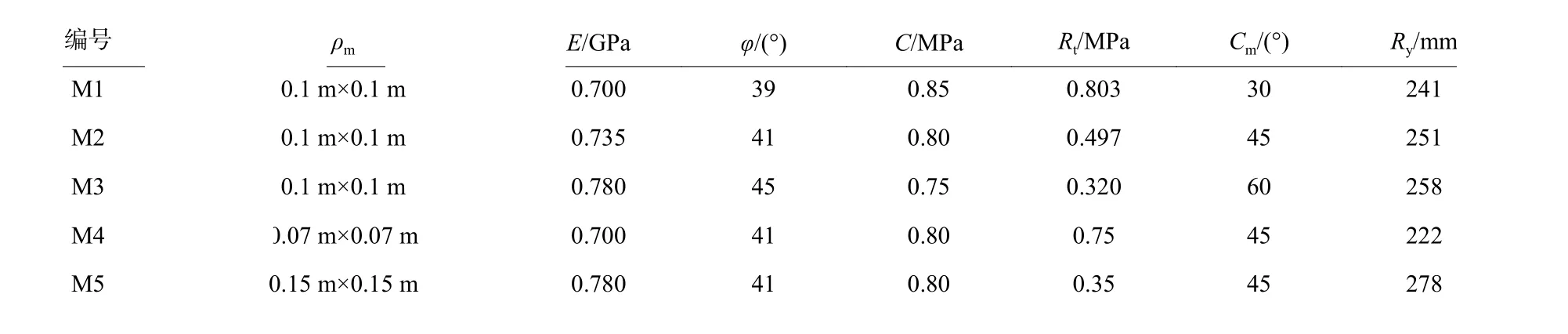
表 4 数值模拟计算方案Table 4 The proposal of the numerical simulations

在计算过程中，我们发现介质爆腔的形状及变形规律基本一致。通过对比前3 个数值结果可知，随着锚索角度的增大，压缩半径稍有增大。同时，加入锚索后测得介质的抗压强度变化不大，我们认为锚索角度变化对介质压缩半径影响不大。

通过比较M2 与M4、M6 的计算结果可知，随着交叉锚索密度的减小，压缩半径不断增大，M6 与M4 的差异可达25%。考虑到锚索密度较大时，使得材料变形消耗巨大能量，因此认为锚索密度变化对介质压缩半径有一定影响。交叉锚索密度对介质破坏范围影响显著，锚索加固介质的破坏半径比起未加固介质的破坏半径小很多，大约在30%左右。三种不同密度锚索加固介质中，测点5 的峰值应力分别为：3.22、4.26、5.93 MPa。可知锚索越密集加固介质中自由场压缩波峰值应力降低越快，主要是因为锚索的变形会消耗大量的爆炸能造成的。