基于反向撞击法的JB-9014 炸药Hugoniot 关系测量*

2019-06-21裴红波刘俊明舒俊翔黄文斌郑贤旭

爆炸与冲击 2019年5期

裴红波，刘俊明，张旭，舒俊翔，黄文斌，郑贤旭

（1.中国工程物理研究院流体物理研究所，四川绵阳 621999；2.中国工程物理研究院研究生部，四川绵阳 621999）

炸药的冲击Hugoniot 关系是指炸药从同一初始状态出发，经过不同的冲击压缩达到终态的集合[1]。它反映了冲击波后炸药热力学状态量之间的关系，其对标定未反应炸药的状态方程、研究炸药的冲击起爆、进行爆轰数值模拟以及理解爆轰反应区结构具有重要的意义，实际应用中使用最多的炸药Hugoniot 关系就是炸药中冲击波速度D 与波后粒子速度u 之间的关系。大量实验表明，在凝聚介质中冲击波的速度D 与其波后质点速度u 之间，在相当宽的速度范围（或压力范围）存在着线性关系[2]：

式中：a 和b 为待定系数，需要通过实验测量确定。

到目前为止，已经有多种测试炸药冲击Hugoniot 关系的方法，如楔形药实验法[3]、冲击波速度对比法[4]、压力对比法[5-6]、速度对比法[7]、组合式电磁速度计法等[8-9]。测试手段方面，采用的有电磁速度计[3,7-11]、扫描相机[3-4]、VISAR[10-11]、锰铜压力计[5-6,12-13]等。由于炸药为不导电材料，常被用来测量金属材料的电探针技术在测量炸药冲击Hugoniot 关系中应用较少。在加载技术方面，近年来采用的主要是气炮加载、透镜加载。相比于炸药透镜加载，火炮或者气炮加载平面性更好，而且更易控制和测试输入压力的大小。不同于金属等惰性材料，炸药在强冲击波作用下会发生反应，这就要求测试所用的传感器具有较短的响应时间，否则仪器记录到的就是一部分反应后炸药的冲击Hugoniot 状态，从而给测试数据引入较大的不确定度。锰铜压力计、电磁速度计响应时间一般大于20 ns，楔形药实验通过扫描相机测量冲击波在炸药中的传播轨迹，获得的是一段时间内冲击波的平均速度，其响应时间也较长。此外，受传感器标定、安装、电路干扰等因素的影响，上述测试方法的精度普遍不高，导致测试数据分散性较大，通常需要进行多发实验来获得较准确的冲击Hugoniot 关系。因此，有必要发展新的测试方法，提高炸药冲击Hugoniot 数据的测试精度。

PDV（photonic Doppler velocimetry）是近年来新发展的一种激光干涉测试技术，其具有使用方便、响应快、测试精度高等优点，被广泛应用于各种爆炸、冲击测试[14-15]。传统的冲击Hugoniot 测试中，样品都是固定不动的，一般通过炸药或者火炮驱动飞片撞击样品，使样品中产生冲击波，这种方式下难以通过激光干涉法测量撞击面的粒子速度。一个可行的办法就是将样品作为飞片去撞击透明光学窗口，然后根据冲击波阵面上的守恒条件计算炸药样品的冲击Hugoniot 关系。谭叶等[16]利用该方法成功获得了惰性材料Bi 的冲击Hugoniot 数据。

以三氨基三硝基苯（TATB）为基的塑性粘结炸药，由于其良好的安全性能，在军事上获得了广泛的应用。例如：JB-9014 炸药是以TATB 为基的塑性粘结炸药，其配方组分为质量分数95%的TATB 和5%粘结剂，典型装药密度为1.895 g/cm3，对应的爆速为7.66 km/s。已有JB-9014 炸药冲击Hugoniot 数据不确定度较大[6]，且与类似配方PBX-9502 的Hugoniot 数据存在较大差异，有待进一步研究。本文中，在火炮平台上，采用反向撞击法通过PDV 技术测量JB-9014 炸药的冲击Hugoniot 数据，拟合得到JB-9014 炸药的冲击Hugoniot 关系，并与已有的文献报道数据进行比较，以期为深入开展JB-9014 炸药的冲击起爆、反应区结构研究以及爆轰数值模拟奠定基础。

1 实验方法

1.1 实验原理

反向撞击法是将待测样品作为飞片安装在弹托上直接撞击镀膜LiF 窗口，其原理如图1 所示。在拉格朗日坐标系中，安装在弹托上的炸药样品经火炮加速后以终速W 撞击静止镀膜LiF 窗口，样品和窗口中将分别产生左行和右行冲击波，样品和窗口中的压力、粒子速度等状态也由p0s、u0s、D0s、p0w、u0w、D0w变为ps、us、Ds、pw、uw、Dw。

由冲击波的基本关系式可知，在一维平面情况下，冲击波阵面的质量和动量守恒，其方程分别为:

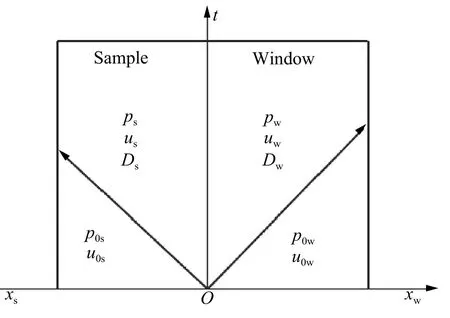
图 1 实验原理图Fig.1 Schematic diagram of experimental principle

联立式（2）和式（3）可得：

式中：ρ、D、u 和p 分别为冲击波阵面后的密度、冲击波速度、粒子速度和压力，下标0 表示初始状态。在欧拉坐标中，根据界面连续性条件可以得到：

根据式（4）和（5），炸药样品和LiF 窗口中冲击波后压力可分别表示为：

联立式（6）～（8），得到炸药样品内的冲击波速度：

式中：ρ0s和ρ0w分别为样品和窗口的初始密度。窗口材料的D-u 曲线一般满足线性关系：

式中：aw和bw为窗口材料的Hugoniot 参数。联立式（9）～（10）可得：

根据式（5）和（11），在已知窗口材料Hugoniot 参数的条件下，利用反向撞击法测量炸药样品的Hugoniot 参数时，只需要测量样品击靶的速度W 和波后粒子速度uw，即可获得炸药样品中波后粒子速度us和冲击波速度Ds。

1.2 实验装置

实验在口径为57 mm 的火炮上进行，JB-9014 炸药样品尺寸为 ∅30 mm×20 mm。装置示意图如图2所示，装置实物图如图3 所示，将圆柱状的JB-9014 炸药样品安装在弹托上，利用口径为57 mm 的火炮将弹托发射至终点弹道速度W，并且撞击LiF 光学窗口。LiF 窗口的尺寸为 ∅20 mm ×11 mm，其撞击面一端镀有约0.7 μm 厚的铝膜，一般冲击波在铝膜内反射2～3 次后压力可达到平衡，据此估算窗口的响应时间约为0.6 ns。LiF 窗口通过支架安装在炮管正前方，安装时利用工装确保炸药撞击面与炮管轴线垂直，在火炮直径57 mm 范围内，飞片加载的平面性优于10 ns。利用光子多普勒测速仪（PDV）同时测量样品击靶速度W 和窗口的界面粒子速度uw。PDV测速探头的直径为3.2 mm，探头输出激光的焦斑直径小于0.3 mm，探头距离窗口反射面的距离约为35 mm。实验前对爆炸罐抽真空，实验时爆炸罐内压强小于200 Pa，激光测速探头通过爆炸罐上的光纤法兰与罐外仪器设备相连。

图 2 实验装置示意图Fig.2 Schematic diagram of experimental device

图 3 实验装置实物图Fig.3 Physical diagrams of experimental devices

实验中使用光子多普勒测速仪CAEP-PDV-3，该测速仪为全光纤结构，结构较紧凑。PDV 使用的激光波长为1 550 nm，当被测物体的运动速度为1 km/s 时，对应的差频频率为1.29 GHz。该PDV 的光电探测器的带宽为12.5 GHz，与其配套的采集示波器带宽为13 GHz，示波器最高采样速率为40 GS/s，受PDV 探测器带宽的限制，该系统最高可以测量约9.7 km/s 的速度。PDV 装置的具体结构及测速原理可参考文献[14]。

2 结果与讨论

进行了4 发实验，测量了JB-9014 炸药样品在3.1～8.2 GPa 压力范围内的样品击靶速度W 和样品/窗口界面粒子速度uw，获得的界面粒子速度如图4 所示。从图4 可知，反向撞击法中，炸药样品直接与LiF 窗口撞击，界面粒子速度迅速上升，紧接着是一个很平坦的平台，平台速度即为窗口的冲击波后粒子速度uw，平台阶段粒子速度的变化幅值小于1%。在1 μs 内炸药界面粒子速度没有出现上升，表明冲击加载下JB-9014 炸药没有发生明显反应，实验中最大加载压力为8.2 GPa，要小于JB-9014 炸药的临界起爆压力（约10 GPa）。如果撞击过程中炸药发生了反应，则界面粒子速度会出现上升，因此，通过该方法可以对炸药的反应情况进行检测，便于判断实验是否测得真实未反应炸药的冲击Hugoniot 数据。实验测得的飞片速度W 如图5 所示，图5 中的时间零点为炸药撞击LiF 窗口界面的时刻。从图5 可知，炸药撞击窗口前速度较稳定，近似于一条直线，实验测得的撞靶时刻附近飞片速度变化小于0.1%。

图 4 样品/窗口界面粒子速度Fig.4 Particle velocity at interface between sample and window

图 5 飞片速度曲线Fig.5 Flyer velocity-time curves

根据实验测量的飞片速度W 和窗口界面粒子速度uw，利用式（8）和（11）计算得到JB-9014 炸药的冲击波后压力、冲击波速度等参数见表1。数据处理中涉及的LiF 单晶Hugoniot 参数为：ρw=2.641 g/cm3，aw=5.176 km/s，bw=1.353[17]。

表 1 实验测试结果Table 1 Experimental results

利用反向撞击法得到JB-9014 炸药样品的Ds-us关系如图6 所示。从图6 可知，在测试压力范围附近，本文的实验结果与Dick 等[3]的类似配方PBX-9502 的实验结果较一致，且本文测试结果分散性更小。与张旭等[6]给出的数据相比，本文测得的数据整体偏高。张旭等[6]给出的数据由锰铜压阻计获得，锰铜压阻计测量精度与压阻系数的标定精度、封装保护等因素有关，另外由于锰铜压阻计测量的是电信号，实验过程易受干扰，因此，该数据的分散性较大。

采用反向撞击法测量J B-9 0 1 4 炸药冲击Hugoniot 数据的实验中，不确定度主要源自窗口界面粒子速度、飞片速度和窗口材料的冲击Hugoniot参数。对于飞片速度，PDV 测速的相对标准不确定度约为0.1%；对于窗口界面粒子速度，PDV 测速的相对标准不确定度约为1%；如果窗口材料冲击Hugoniot 参数的相对不确定度按照0.5%计算，则根据不确定度的传递规律，采用反向撞击法获得的样品粒子速度相对合成标准不确定度约为1%，冲击波速度的相对合成标准不确定度约为1.8%。

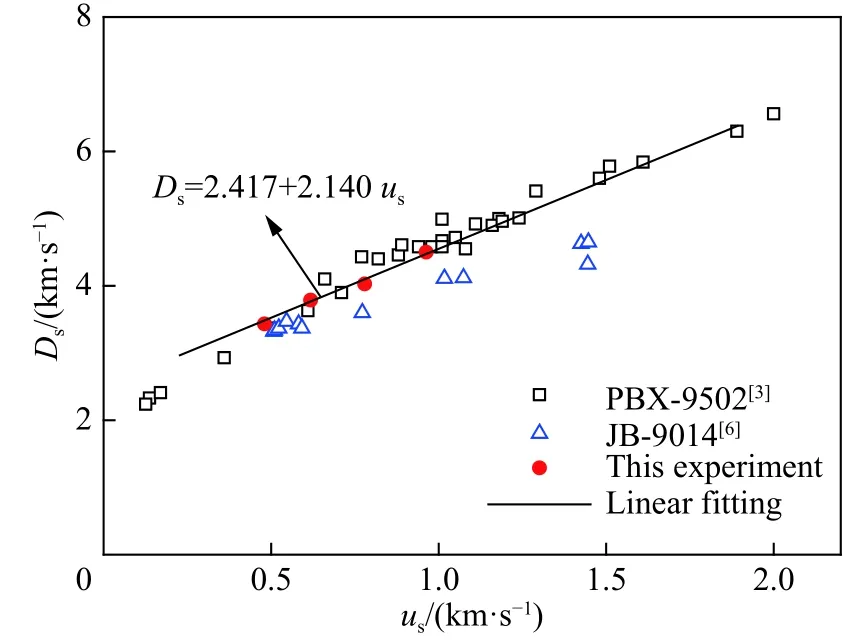
图 6 炸药样品的冲击波速度与粒子速度的关系Fig.6 Relation between shock velocity and particle velocity for the explosive samples

由上述结果可知，采用反向撞击法测量炸药冲击Hugoniot 参数是可行的，实验中主要参数均采用PDV 测量，数据不确定度要小于楔形药法、压力对比法、粒子速度对比法等方法的。受火炮加载能力的限制，本文中暂时没有开展更高加载压力的实验，根据已有的实验结果，反向撞击法测试的响应时间约为5 ns，该值要明显低于锰铜压阻计、电磁速度计的响应时间，通过提高弹托的发射速度，有望得到更高压力下未反应炸药冲击的Hugoniot 数据。