“游戏”人生——行为博弈论

☉董志勇

“博弈论”的英文是“game theory”，game的本意是游戏，博弈论直接翻译成中文最贴切的是“游戏理论”。更确切点说，是一种竞合的智力游戏。博弈论作为经济学的一个分支，自出现以来，在学术领域和社会生活的各个方面都得到了广泛的认可和应用。事实上，在传统经济学研究范式的框架下，标准博弈理论一直以“理性人”为理论基础，通过一个个精美的数学模型搭建起公理化的完美自洽的理论体系，却往往忽视了日常生活中人们的实际行为。

然而，心理学和行为经济学的研究结果表明，人类在做出决策时并不总是“理性”的。在标准博弈论的基础上，行为经济学家从人自身的心理特质、行为特征出发，去揭示博弈中影响选择行为的非理性情感因素。他们为了弥补传统博弈论理性人假定的不足，经过多年理论和实证研究，提出了“行为博弈论”。

在这一章中，我们就将接触到许多有趣的行为博弈实验，它们充满了逻辑与推理，需要仔细思考，才能体会到行为博弈的奇妙之处。

买扑克与打扑克的心理战——讨价还价博弈

独裁者游戏

实验一，博弈者A与博弈者B分配一定数额的金钱（假设是10元）。其中A出价，也就是在双方之间分配这一利益，要求B要么接受要么拒绝，如果B接受，那么双方就按照A提出的分配比例瓜分，如果B拒绝，那么双方之间不会有交易行为，双方都不会获得任何收益。按照传统博弈论的推导，博弈者都是理性自利的，有收益总是比没收益好，因此只要A对B的分配大于0，理性的B都会接受。

传统博弈论的分析结果显然是，A获得绝大部分利益，B只能分得蝇头小利。然而行为博弈论的实验表明，出价者的平均出价大致是4～5元左右。50%的B都拒绝了2元以下的出价，B认为过分低于1/2的出价太不公平，因此以拒绝的方式惩罚对方的行为，结果双方的收益都是0元。如果A出价过低，B的拒绝实质上是一种“报复性回报”。这就是说，回应者宁愿牺牲自身的利益去惩罚那些未公平对待他们的出价者。

实验二，两个实验参与者要从有4张“A”与4张“2”的扑克牌中随机各抽4张，这样保证参与者可以通过自己手中的牌推断出对方的牌。参与者被告知4张“A”共值10英镑，如果“A”少于4张，则一文不值。因此为了赢钱，参与者需要将“A”汇集起来，再对如何分配10英镑进行讨价还价。实验结果表明，当双方都有两个“A”时，他们达成了明确的均分协议，但是当一个人拿了1张“A”，另一个人拿了3张“A”时，就产生了不协调，一部分参与者要求对半分，而另一部分要求报酬与持有“A”的比例相似。

行为经济学原理：之所以出现这种不协调，是因为在讨价还价中存在自利性偏向，参与者认为对于自己有利的就是公平的。在现实生活中，正是这种自利性偏向阻碍了许多协议的达成。

一个真实的法律案件为解决讨价还价的问题提供了一种思路。原告因为在一场交通事故中受到伤害而向肇事者提起诉讼，要求赔偿损失，赔偿的数额由双方讨价还价决定，同时双方商定协议的时间越长，诉讼费就越多。开始双方一直争执不下，最后发现在罗列完双方各自在事故中所犯的错误后，协议达成的可能性就大大增加了，这就说明了在讨价还价过程中仲裁的重要性，因为他们可以无偏见地指出案件的各个方面，包括双方在案件中犯的错误，同时他们还可以提出一个妥协的解决办法。这也为解决日常生活中的争端提供了启发，比如在处理国际事务时，联合国与世界贸易组织就可以担当仲裁人的角色，当然，最后能否达成协议还要看协议双方达成一致的意愿。

扑克与博弈

有一个扑克牌游戏的规则是这样的：每个玩家依次发牌，每发一轮牌必须下注，不下注的玩家自动退出游戏。在最后摊牌之前，玩家都隐藏自己的牌，最后推牌后，牌最大的玩家获胜。在玩这种扑克牌游戏时，信息是不充分的，因为你不知道对方的底牌是什么，你需要分析对手的行动，对手小额下注究竟是牌小的表现还是故意引诱你抬高赌注？大额下注意味着大牌稳操胜券还是虚张声势？同时你还要防备别人对自己的试探。

在现实的讨价还价中，信息往往是不充分的，比如卖者通常比买者更了解所卖商品的信息，而买者比卖者更清楚该商品对于自己的价值。因此讨价还价就产生了两个目的，既要获得最大收益又要传递信息，而这两方面有时是不能同时达到的，因此就降低了效率。

经济学家发现交流可以增加交易的效率，但是大部分不是通过互相说出实情得到的，而是根据行为语言试探得到的。因为卖家的报价往往会高于商品的实际价值，而买家的报价往往会低于商品对于他的价值，实验表明参与者会明显地试探对方的保留价值，然后协调一种大家都能够接受的价格。这同时也说明了面对面交流会比书面交流更有效。

你猜我在想什么——行为博弈案例

或左或右的发球

我们考察了1974年到1997年中十个大满贯的网球决赛结果，选手都是最顶尖的网球选手。研究考察的是选手发球在左边和右边的得分概率。如果对发球的方向没有偏好，左边和右边的概率应该一致。研究结果证明了这一猜想。选手发球在左边和右边的得分概率十分相近。另外，结果也显示，尽管是顶尖选手，他们也倾向于在前后两次的发球中交替选择左边和右边，但这种偏差的程度略小于一般人的程度。

我们再考察在足球比赛中罚球踢向左边和右边的进球率，结果发现，运动员不管踢左边还是踢右边，进球率是一致的。并且他们也没有这次踢左边下次就踢右边的偏误，但这点并不令人惊讶，因为通常球员很少被连续罚球，他们记忆中的“序列相关性”的偏误就会降低。

行为经济学原理：心理学家和神经科学家认为，人的大脑中有一种随机结构。很多实验证明，无论是要求被试以某分布概率随机选择策略，还是直接给被试以某种随机任务，相对于理论上的随机概率分布而言，都会产生以下两个方面的偏离：人们总是过多地交替变换他们的反应，并容易忽视样本大小。

第一种偏离基于人们对“序列相关性”的误解，即在重复博弈中，人们总是认为前后两次博弈的策略是有相关性的，为了增加最后取胜的可能性，前后两次博弈采用的策略应该不同才好。比如，在“猜硬币”游戏中，猜硬币者上一次猜的是“正面”，下一次就很可能猜“反面”，因为他们觉得刚刚出现一次正面，下一次出现反面的概率更大些，而事实上，前后两次硬币的正反面没有任何关系。另外，在“剪刀-石头-布”的猜拳游戏中也有这种情況。如果参与者上一次出了“剪刀”，下一次就很可能不再出“剪刀”。再如，人们在买彩票时，如果某一数字序列刚刚中过奖，那么很少有人会再选择这个序列，但事实上，这一序列和其他序列中奖的概率是相同的。

第二种偏离是人们在预测结果时，常常会错误地应用一些只有在样本量很大时才会出现的性质。以最简单的掷硬币为例。在样本量很大（比如掷1000次）的时候，硬币正面出现的频率和反面出现的频率都应该是1/2。而当样本量很小（比如只掷10次）时就不一定了。但人们却仍会认为正反面出现的频率是相等的。

选美比赛博弈

选美比赛博弈是来源于凯恩斯的《就业、利息和货币通论》，凯恩斯把股票投资比作选美比赛，为了获胜，参与者不会选择自己认为最美的人，而会去猜测哪个是最能抓住别人眼球的美女。当所有人都持有同样的想法时，选美比赛便违背了它的初衷，演变成了预测大众看法的比赛。

行为经济学家在课堂上经常会做这样简单的实验：参与者被要求在0到10选择一个数字，胜者是选择的数字最接近所有参与者均值的2/3的那个人。同选美比赛类似，参与者必须预测别人所选的数字的均值，然后选择均值的2/3。

这个实验可以检测参与者在进行选择的过程中进行了多少轮的重复推理。如果每个参与者都随机选择，则均值是50，50的2/3是33，所以选择33的人进行了一步占优，如果有一个参与者预测所有人都进行了一步占优，他就会进行二步占优从而选择33×2/3＝22，同样道理，进行三步占优的人会选择22×2/3＝15……当进行了无穷多步的重复占优后，我们可以得到最终的重复占有纳什均衡是0。

行为经济学家对这个博弈进行了实验研究，实验对象是多组14～16周岁的德国学生，得到的实验结果是35左右。我们自己对北京大学总裁班的CEO、证券经纪人等也进行了相同的多次实验，得到了相似的实验结果。另一个有趣的实验对象群是财经杂志的读者，在对其进行实验时提供了大额的奖金，也得到了相似的结果，均值位于33与22之间，而且只有8%的实验对象选择了0。因此，在选美比赛博弈中，实验对象一般只能进行一到两步的重复推理。

行为经济学原理：对于这个结论有两种解释，一是参与者无法进行多次的重复推理；二是参与者不相信别人能够进行如此多重复推理。这就是西蒙所讲的有限理性；人的思维能力并非无穷无尽；人具有的是有限理性；因为人是有限理性的，所以人们在行为上并不总是追求效用极大化。实际上，人会根据对环境的认知和自己有限的思维，做出让自己满意即可的选择。这就是更接近血肉之躯的人的“有限理性”的观点。

爱情蜈蚣博弈

谈恋爱其实也可以看作一种博弈，男女双方从开始的简单了解，通过多次接触后达到信任，最后生活在一起，就是一种由浅入深的试探过程，双方在互相接触中看对方能否使得自己实现利益最大化。

博弈实验小王和小花是这个故事的男女主角，他们在谈恋爱的过程中都有两种选择：一种是“继续”，即让对方做出选择，而由于双方了解程度加深，两人的爱情总收益在不断增加；另一种是“甩”，即结束恋爱。这种博弈实际上是一种多阶段的信任博弈，每个参与者既希望通过信任对方获取更大的利益，又担心因信任产生的风险。

经济学家用实验模拟了“蜈蚣博弈”，结果如下：

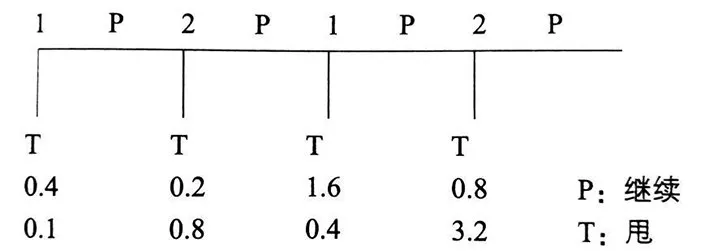
博弈从左到右进行，在第一轮交往中小王可以先做出选择，如果他选择“甩”，那么小王和小花分别得到0.4和0.1的爱情收益。如果小王选择“继续”，则轮到小花做出选择，她选择“甩”，那么小王和小花分别得到0.2和0.8的爱情收益。可以看到两人爱情收益的总和是第一轮的两倍，但是小王得到的比第一轮少，小花得到的比第一轮多。显然，被甩的人受的伤害比较大。如果小王和小花每次都选择“继续”，他们一起走到最后收获圆满爱情，将获得6.4和1.6的最高收益。但是当我们用倒推法就会发现这样圆满的结局很难达到，在第四轮时，小花的最优策略是选择“甩”，因为继续下去收益不会增长。因此对于小王来说，如果在预料到小花在第四轮一定会选择“甩”，那么他在第三轮时的最优策略也应该是“甩”。这个结果就如同囚徒困境，理性的选择并不能达到最优解。每次行动都选择“传递”虽然能够达到帕累托最优，但是却破坏了重复占优均衡，这说明完全自利的行为会导致合作的破裂。

以上是标准博弈理论所作的均衡分析。但是在现实生活中很少有人在恋爱的初期就选择分手，说明恋爱过程中双方并非完全理智，道德习惯、学识都可以影响这一过程。

我们可以用一个均衡模型来解释“继续”的高比例，模型中把“继续”的原因分为两类，一类是利他主义者从内心偏好“继续”，另一类是普通参与者通过在某步之前“继续”而把自己伪装成利他主义者，目的是获得更多收益，这部分人占了绝大多数。