SVD样本学习的嵌入式智能吹风系统设计

孙立书

摘  要： 针对传统吹风系统不能根据环境温度和光照强度实现智能化多档位调整的缺点，设计一款基于奇异值分解的样本学习的新型多档位自动调节智能吹风系统。该系统以STM32F407ZGT6最小系统为控制核心，采用温度传感器和光敏二极管实时采集环境温度和光照强度。利用奇异值分解的最小二乘算法，根据周围的温度与亮度参数，利用最小二乘方法做线性拟合，预测出当前所需要的电机转速。实验结果表明，该系统能够根据用户习惯，随着环境温度和光照强度，实现多档位智能调速，以满足不同用户的需求。

关键词： 智能吹风系统; 奇异值分解; 多档位调整; 最小二乘算法; 样本学习; 线性拟合

中图分类号： TN915?34                     文献标识码： A                           文章编号： 1004?373X（2019）10?0171?04

Design of intelligent embedded blowing system based on SVD sample learning

SUN Lishu

（Jiangsu University of Science and Technology， Zhangjiagang 215600， China）

Abstract： In allusion to the disadvantage that the traditional blowing system cannot realize intelligent multi?switching adjustment according to the environmental temperature and illumination intensity， a new multi?switching automatically?adjusted intelligent blowing system based on sample learning of singular value decomposition （SVD） is designed. In the system with the STM32F407ZGT6 minimum system as the control core， the ambient temperature and illumination intensity are collected in real time by using the temperature sensor and photosensitive diode. In accordance to the ambient temperature and luminance parameters， linear fitting is conducted by using the least squares algorithm based on SVD， so as to predict the currently?needed rotation speed of the motor. The experimental results show that the system can realize multi?switching intelligent speed adjustment with variation of ambient temperature and illumination intensity according to user habits， so as to meet the needs of different users.

Keywords： intelligent blowing system; singular value decomposition; multi?switching adjustment; least squares algorithm; sample learning; linear fitting

0  引  言

随着人工智能技术的发展，人们对家用电器设备的使用要求越来越高，不仅要功能强大，而且要更加智能化、节能。针对以往家用电吹风系统功能单一，不能根据环境温度和光照强度实现智能化多档位调整的缺点，设计一款基于SVD样本学习，能根据环境温度和光照强度实现多档位自动调节的电机转速系统，从而实现智能吹风系统的设计。基于温度和亮度控制的智能调速吹风系统，即电机的转速是由外界实时温度和太阳光亮度进行智能调节。将外界温度、太阳光的亮度与电机转速的对应关系表示成：V（电机转速）=F（T&BRI）。

在以往的设计中这种对应关系是设计者在软件设计时就设定好的，无法更改。比如设置温度 29～38 ℃之间平滑对应电机速度的1～10档，自动调速。但是这种智能调速方式不一定适用于所有人（有的人可能在 33 ℃就希望电机打到10档），如果采用手动方式调节电机转速，就显得不智能。因此设计开发一套能够根据用户习惯，随着环境温度和光照强度，实现多档位智能调速，以满足不同用户需求的吹风系统就显得非常的必要。为了能够让温度与电机速度的对应关系能够智能适应各种用户需求，就必须采用一种算法使得电机转速和温度的对应关系是根据用户习惯来确定的（机器学习）。

1  系统设计原理

本系统通过机器学习[1]，即概率的方式，运用随机样本建立起一个待求参数的数学映射模型，运用此模型来预测输出空间的值。机器学习包含回归分析、分类器等算法，本文采用机器学习中的回归分析。其采用基于SVD（奇异值分解）的最小二乘算法，根据周围的温度与光照强度参数，并利用最小二乘的方法做线性拟合，从而预测出当前所需要的电机转速。即外部温度与光照强度到电机 PWM 占空比的映射，则是通过奇异值分解（Singular Value Decomposition）实现的最小二乘方法（Ordinary Least Square）。建立针对符合样本特征的模型，通过建立的模型进行电机转速预测。此系统仅仅利用线性映射做高维的线性拟合，模型选择线性函数。对于不同温度以及不同时段（光照强度）下每个人喜欢的吹风系统速度不同，这个抽象的特征则可以通过调节人给定的样本大体反映，可以保证样本的有效性。该系统的温度通过温度传感器来采集，亮度通过光敏二极管来采集，电机的转速（V）通过PWM控制。设电机转速和温度以及亮度之间的表达式满足：

[PWM=θ0+θ1·Temp+θ2·Brig]  （1）

式中，[θ0，θ1，θ2]三个参数是由用户操作后通过 SVD 最小二乘算法确定的。此系统利用机器学习算法，达到了智能化控制的目的。预测的主要过程分为两个阶段：学习过程与执行过程。

1.1  学习过程

该系统模型是三维空间的一条超直线，由线性代数可知，当样本数量大于参数数量时，没有标准解，但存在最优解，也就是最优的系数[θi]，包含这几个系数的确定模型，在给定样本输入空间的参数后，能最近似地表示出样本输出空间。通过回归方法，以及从每个人的喜好中获得以下形式的样本，如下：

[Tempi，Brigi，PWM（i）]   （2）

式中，上标i表示第i个样本，i的个数一定要大于参数个数。学习出以下线性模型中[θ0，θ1，θ2]，如下：

[P=PWM=θ0+θ1·Temp+θ2·Brig]  （3）

不同的样本学习出的参数不同，学习出的常量参数记为[θ0，θ1，θ2]。全局最近似是m个样本根据模型预测的输出空间值和样本输出空间值之间误差的欧氏距离最小，[Dglobal=b-Aθ=i=1m（P（i）-f（xi））2]。其中[b=P（1）P（2）P（3）…P（m）T] ， [A=1Temp（1）Brig（1）???1Temp（m）Brig（m）] ， [θ=[θ0，θ1，θ2]T]，[x（i）=[Temp（i），Brig（i）]] 。要使[Dglobal]最小，根据向量求導法则，且根据凸函数的性质，所求极值点为最小值点，即[?Dglobal?θ=0]，可以导出：

[θ=（ATA）-1ATb] （4）

则可以求出最优值[θ]。

1.2  执行过程

该过程是利用[θ0，θ1，θ2]这3个参数以及当前的温度亮度状态，得出经过预测的 PWM 的占空比，进而调节电机的转速。

[PWMnow=θ0+θ1·Tempnow+θ2·Brignow]

式中：[PWMnow]指通过学习出参数的模型预测出的占空比;Tempnow指当前周围的温度;Brig now指当前周围的亮度， 此学习系统输入空间是二维，分别是温度与亮度，输出空间是一维，是 PWM 的占空比。在不同的样本下，会出现不同的[θi]的组合，进而在一个三维空间中，PWM 的占空比按着学习出的模型参数，以及外部的温度与亮度的参数变化而变化，从而达到了根据环境的变化（输入空间值）以及人为的样本学习（参数）来预测最终的电机速度，实现了简单的智能化。

1.3  最优值[θ]的求解

利用最小二乘法求[θ]的最优值。由于数学运算和数值计算之间的差别，导致算法精度降低，因此使用奇异值分解计算伪逆[2?4]。利用伪逆计算最小二乘法[3]，[θ=VΣ-1UTb]，其中，[U，Σ，V]是奇异值分解A得出来的3个矩阵，[Σ-1]是[Σ]的伪逆矩阵。根据此公式，利用矩阵乘法运算，即可计算出最优值。文献[2]中给出奇异值分解的多种算法，在此，选取两个过程来计算奇异值分解（“+”为非零元素）：

1） 首先将任意m×n矩阵A通过左右 Householder变换[5?6] ，变换成双对角矩阵J。其中[PprodAQqrod=J]，[Pprod]与[Qqrod]均为单位正交矩阵，因此：

[A=PTprodJQTprod] （5）

式中：[A=+++++++++];[J=++00++00+]。

2） 计算JTJ与JJT，这两个矩阵都是三对角矩阵，且是对称阵。

利用旋转变换[7?10]的算法，计算出JTJ与JJT的特征值与特征向量[11?14]，并从大到小进行排序，JTJ与JJT的特征值相同，JTJ的特征向量是J的右特征向量V1，JJT的特征向量是J的左特征向量U1。对奇异值矩阵的对角线进行排序，并且同时改变左右特征向量的顺序，与之前的 Householder 变换矩阵相乘，得到双对角矩阵的 SVD：

[J=U1ΣVT1] （6）

3） 将式（6）代入式（5）得到：[A=PTprodU1ΣVT1QTprod] ，令 [U=PTprodU1]，[V=QprodV1]，则：

[AI=VΣUT] （7）

根据奇异值分解的结果做伪逆，如下：

[θ=AIb=VΣUTb] （8）

详细证明在文献[2]。

2  系统硬件设计

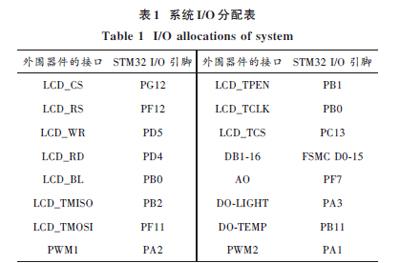
该系统主要包括电源部分、系统控制核心和显示部分、传感器部分、电机驱动与电机部分。电源部分包括7.2 V电池、LM1117?5 线性稳压芯片（将7.2 V电源转换成5 V电源）、LM1117?3.3 线性稳压芯片（将7.2 V电源转换成3.3 V电源）。系统采用2.8寸TFTLCD液晶屏作为GUI 界面显示，采用STM32F407ZGT6作为控制核心，选用F4系列主要为了打开FPU模块加快浮点运算[15]，采用温度传感器 DS18B20采集温度，采用光照传感器光敏二极管采集光照亮度信号，采用BTN7971驱动芯片，直接驱动大电流电机RS540?SH。系统硬件实物图如图1所示。系统I/O分配表如表1所示。

3  系统软件设计

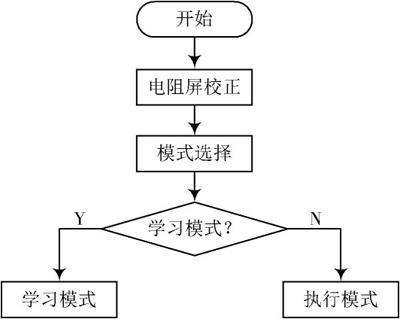
从机器学习原理来看，该系统的主函数包括学习过程与执行过程。学习过程即先进行学习，学习出[θ]，再利用学习出的模型进行结果预测，对应主程序流程图为图2的左侧分支;执行过程是直接使用系统中给出的样例[θ]求结果，对应主程序流程图为图2的右侧分支。

图2  程序主程序流程图

4  系统调试与实验结果

打开电源，校正电阻屏幕，出现模式选择界面，选择执行模式，利用样例预测 PWM。样例一模型的特征是当温度和光照强度变大的时候，电机转速变快;样例二模型的特征是当温度和光照强度变小时，电机转速变慢。按下 Pause暂停，自由选择 Sample1 或Sample2 来改变模型参数;然后按下 CONT 继续执行程序，使得电机转速跟着当前环境的温度与光照强度进行变化，如图3所示。返回模式选择界面，选择学习模式，如图4所示，上方Temp为实时温度，Brig是实时光照强度，PWM 通过下方的进度条进行调节。给定样本的输出空间参数，当参数合适，按下Record按钮记录下当前的数据，并且此时只有按下 CONT 按钮，才能继续进行记录与擦除。当记录数据不当时，可以按下Erase按钮消除最近一次的记录，同时也要按下CONT键才能继续记录与擦除。调节传感器状态，调节PWM进度条，给定4个样本，经过多次记录与擦除修改，给出有一定线性关系的样本，如图5所示。当4个样本输入结束后，进行最小二乘运算，结束后显示COMPLETE字样，自动进入执行模式，利用样本学习出的模型参数进行预测，Temp是当前的温度值，Brig是当前的亮度值，PWM是当前通过样本学习预测出的占空比，而中间的式子是初始模型。预测界面如图6所示。根据系统实验结果可知，系统最终给定的样本有四种大体特征，即：温度升高，光照强度增强，电机转速变快;温度升高，光照强度减弱，电机转速变;温度降低，光照强度增强，电机转速变快;温度降低，光照强度减弱，电机转速变慢。每种特征都对应无穷多种小特征，即温度或光照强度的变化率对应电机转速变化的趋势，即灵敏度。这是一般吹风系统做不到的，即该系统能根据用户习惯，随着环境温度和光照强度的变化，实现多档位智能调速。这也正是此吹风系统的优势所在。

5  結  论

本文主要利用奇异值分解的最小二乘算法做线性拟合，根据当前环境温度和光照强度，预测当前需要输出的PWM的占空比，进而控制电机的输出转速。实际测试表明，该系统能够根据用户习惯，随着环境温度和光照强度的变化，自动实现电机转速的调整，以满足不同用户的需求。

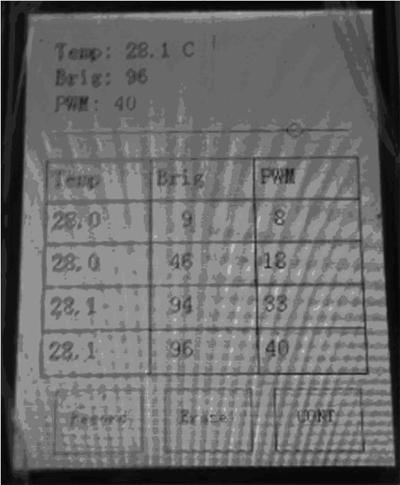
图5  给入样本的学习模式界面

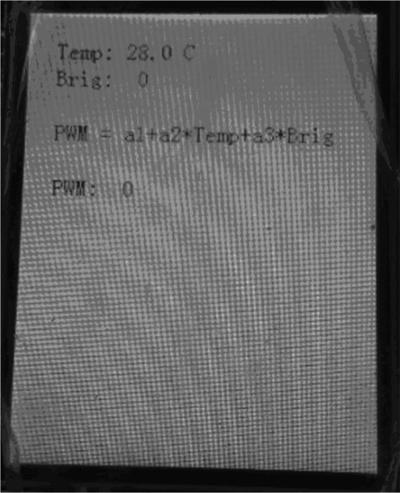
图6  预测界面

参考文献

[1] Anon. UFLDL tutorial. [2013?04?07]. http：//ufldl.stanford.edu/wiki/index.php/UFLDL_Tutorial.

[2] GOLUB G H， KAHAN W. Calculating the singular values and pseudo?inverse of a matrix [J]. SIAM journal on numerical analysis， 1965， 2（2）： 205?224.

[3] KALMAN D. A singularly valuable decomposition： the SVD of a matrix [J]. The college mathematics journal， 1996， 27（1）： 2?23.

[4] GOLUB G H， LOAN C F V. Matrix computations [M]. 3rd ed. Baltimore： John Hopkins University Press， 1996.

[5] PRESS W H， FLANNERY B P， TEUKOLSKY S A， et al. Numerical recipes in C [M]. Beijing： Publishing House of Electronic Industry， 1992.

[6] PRATA S. C primer plus [M]. 6th ed. London： Pearson， 2014.