一种基于属性邻接矩阵和博弈理论的风险控制模型
2019-06-20顾兆军李跃凯
顾兆军 李跃凯

摘 要: 为了网络安全管理员能够在有限的资源条件下及时加固关键节点,减少网络攻击带来的损失,设计一种基于属性邻接矩阵和博弈理论的风险控制模型。该模型利用BFS攻击图簡化算法删减攻击图中出现的环路和冗余节点,将简化后的攻击图转化为属性邻接矩阵,最后利用博弈理论得出可能的攻击路径和最优防御策略。实验结果表明,与传统风险控制方法相比,该模型解决了顶点和边数过多导致图结构过于复杂的问题,更具可视性地得出了攻击路径和原子攻击序列,可为信息系统管理员提供科学的理论参考。
关键词: 风险控制模型; 攻击图; BFS攻击图简化算法; 属性邻接矩阵; 博弈理论; 冗余节点
中图分类号: TN911?34; TP393.08 文献标识码: A 文章编号: 1004?373X(2019)10?0005?05
A risk control model based on attribute adjacency matrix and game theory
GU Zhaojun1,2, LI Yuekai1,2
(1. Information Security Evaluation Center, Civil Aviation University of China, Tianjin 300300, China;
2. College of Computer Science and Technology, Civil Aviation University of China, Tianjin 300300, China)
Abstract: A risk control model based on the attribute adjacency matrix and game theory is designed for the network security administrators to timely consolidate key nodes under the limited resource condition and reduce losses caused by network attacks. In the model, the BFS attack graph simplified algorithm is used to delete the loops and redundant nodes appearing in the attack graph. The simplified attack graph is transformed to the attribute adjacency matrix. The game theory is used to obtain possible attack paths and the optimal defense strategy. The experimental results show that, in comparison with traditional risk control methods, the model can solve the problem of too complex graph structure caused by excessive vertexes and edges, and obtain the attack paths and atomic attack sequence visually, which provides a scientific and theoretical reference for information system administrators.
Keywords: risk control model; attack graph; BFS attack graph simplified algorithm; attribute adjacency matrix; game theory; redundant node
0 引 言
网络安全事件频繁发生,信息系统的安全性变得越来越重要。由于脆弱点,或称为安全漏洞的客观存在,因攻击行为而导致的网络安全事件难以避免。传统防御诸如防火墙、防病毒软件以及入侵检测工具等技术手段难以提前准确地预测威胁。目前我国也未形成标准的防御体系。美国计算机安全协会发布的计算机犯罪和安全调查报告[1]显示,当前网络面临的攻击行为大多表现为多步骤的组合式攻击,其行为采取多个原子攻击的方式逐步完成。原子攻击是指攻击者通过攻击主机上或网络中的某个脆弱点而发起的攻击,一系列的原子攻击构成了一个攻击行为[2?3]。因此,对攻击图中原子攻击和攻击序列的研究尤为重要。
OU X M指出循环路径是攻击图复杂原因之一[4]。HOMER J等人使攻击图不含循环路径,一个节点在任何一条路径中不重复出现,但这样节点增多,攻击图更为复杂[5]。NOEL S等人使用邻接矩阵表示攻击图[6],利用0和1来表示各节点之间是否可达,不能显示出攻击的行为和路径。LYE K W等利用随机博弈形式分析和推理网络攻防双方的博弈关系,验证了博弈论同网络攻防相结合的有效性和适用性[7]。姜伟构造了一个网络防御模型,将博弈论和网络攻防结合,理性预测攻击者可能会采取的攻击行为,但其重点用于攻防双方状态的转换,不能反映攻击路径[8]。李庆朋等人利用脆弱点之间关联性减少大规模网络攻击图中冗余点,但须对原始生成的攻击图进行复杂的预处理,加之目前脆弱点的关联性强度也并不明确,实用性低[9]。
与以上所做工作不同,本文提出一种基于属性邻接矩阵和博弈理论的风险控制模型。
1 风险控制模型
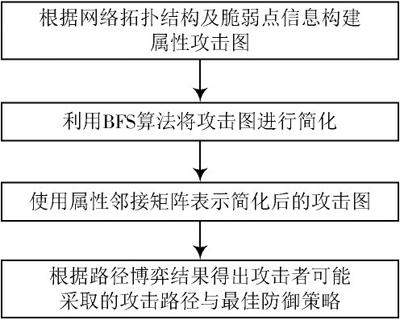
本文利用属性邻接矩阵和博弈理论对系統进行分析的流程如图1所示。

图1 风险控制模型流程图
1.1 简化攻击图
攻击图分为状态攻击图和属性攻击图两种。由于状态攻击图节点过多时存在状态爆炸问题[10?11],执行效率低下,本文采用属性攻击图进行分析。
攻击图G=(C,E)是一个有向图,其中C代表原子攻击节点集合,E代表渗透节点集合,或称为攻击节点获得的属性节点集合[12]。攻击图简化过程为:
1) 计算每个渗透节点父节点个数,预先将每个渗透节点置为FALSE,且将其number_Child值置0。
2) 设定队列q,将初始原子攻击节点依次插入。
3) 按序从q中取出原子攻击节点,将其子节点(渗透节点)number值加1。若number的值与已计算出的该渗透节点父节点的数目相等,说明该节点成功发生条件已满足,将Flag置TRUE,且把该节点的所有子节点(原子攻击节点)依次加入q中。
4) 去除Flag为FALSE节点和与其相连的边,得到简化后攻击图。算法如下:
输入:攻击图G=(C,E)
输出:简化后攻击图
1. Foreach ei [∈]E do
2. Count[ei]=number_Parent[ei];
3. Flag[ei]=FALSE;
4. number_Child =0;
5. Foreach Ci[∈]C do
6. Insert(q,Ci);
7. Foreach k=Delete(q);
8. Foreach ej[∈] Child(k) do
9. number_Child[ej]= number_Child[ej]+1;
10. If number_Child[ej]==Count[ej] Then
11. Flag[ej]=TRUE;
12. Foreach Ct[∈]Child[ej] do
13. Insert(q,Ct);
14. Return 去除Flag为FALSE节点的简化后攻击图
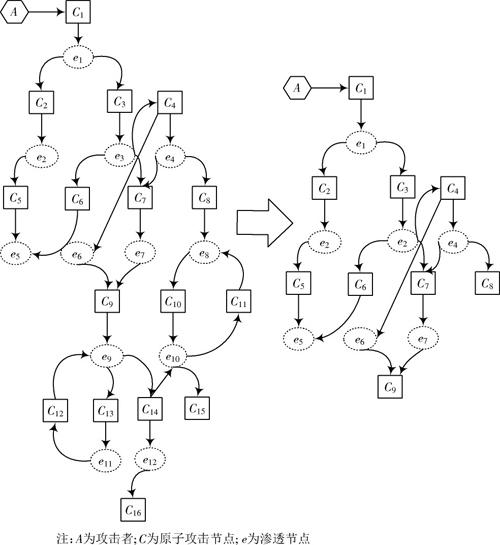
图2左图是某业务系统的原始攻击图。攻击者攻破脆弱点C1可以渗透至e1,接着攻破C2可以渗透至e2和e3,攻破C3可以渗透至e3,直至到达攻击者的目标节点。C1至e1的边称为e1的前提边,e1至C2,e1至C3的边均为e1的后果边。显然,图中e9→C13→e11→C12→e9为一条循环路径,现实场景中不会发生这样的攻击,应予以删减,降低攻击图冗余度和分析难度。同理e8→C10→e10→C11→e8 也应予以删减。简化后的攻击图如图2右图所示。

图2 原始攻击图的简化(一)
1.2 形成属性邻接矩阵
对于n个属性节点的网络,其属性邻接矩[M]是一个n×n的矩阵。mij表示从属性i到属性j的一个原子攻击。mij≠0,说明i到j之间存在攻击路径;mij=0,说明i到j之间不存在攻击路径[13]。
记单步的属性邻接矩阵记为[M],属性ei到属性ej单步的攻击路径记为ei(mij)ej,括号内容表示一个原子攻击行为。
定义1: [i=1nai=a1?a2?…?an(i=1,2,…,n)]。
定义2: [mikΔmkj]为属性[ei]和[ej]之间两个相邻的原子攻击行为,[k]为中间节点。
定义3: [m2ij]代表[ei]和[ej]之间所有的两步攻击路径,[m2ij=k=1n(mikΔmkj)]。
定义4: 设矩阵[A=(aij)m×k],[B=(bij)k×n],记[C=A?B],[C=(cij)m×n]。其中矩阵元素[cij=] [(ai1Δb1j)?(ai2Δb2j)?…?(ai3Δb3j)=s=1k(aikΔbkj)]。
对两步属性邻接矩阵[M2],其元素可表示为[k=1n(mikΔmkj)],那么对于[n]步的属性邻接矩阵,给出下列定理及其证明。
定理1: [n]步的属性邻接矩阵[Mn]中,[ei]~[ej]的所有[n]步攻击路径可表示为[mnij=k=1n(mn-1ikΔmkj)]。
证明:当[n=1]时,[mij]即为攻击行为;当[n=2]时,[m2ij=k=1n(mikΔmkj)]显然成立;假设[n=t]时,[mtij=k=1n(mn-1ikΔmkj)],则[n=t+1]时,[mt+1ij=k=1n(mtikΔmkj)],其中[mtik] 表示[ei]~[ek]的[t]步攻击行为,[mt+1ij] 表示在[t]步攻击行为之后拥有的属性[ek],再进行[ek]~[ej]的单步攻击,原式得证。
图2右图的单步属性邻接矩阵如下:

对此矩阵进行计算得到两步属性邻接矩阵[M2=M?M],其中[m216=(m12Δm26)?(m13Δm36)],表示属性[e1]可以通过[m12Δm26]和[m13Δm36]两种两步连续攻击行为获得属性[e5],路径表示为(e1(C2)e2(C5)e5)∪(e1(C3)e3(C6)e5)。
研究表明,20台主机对应的攻击图也相当庞大复杂[14]。采用属性邻接矩阵来表示攻击图,不仅保留了邻接矩阵的可视性优点,也可直观表示出任意两个节点之间的单步、多步原子攻击序列,降低了理解和分析的难度。相比顶点和有向边的表示方法,该方法不仅适用于小规模攻击图,在较大规模的攻击图中更能体现出优势。
多步属性邻接矩阵的时间复杂度不超过O(n3),n为目标网络中的节点数;而在攻击图中随着节点数的增加,时间复杂度呈指数型增长。
1.3 路径博弈
网络攻防双方的策略依存性正是博弈论的基本观点,从博弈的视角研究网络攻防行为具有较高的科学性和合理性。攻防双方博弈策略的形式可由一个三元组[G=S,T,U]来表示,其中S代表参与者的集合,T代表攻防双方的策略集(即攻防路径的集合),[U]代表攻防双方的效用函数。
定义5:[S={a,d}],[a]代表攻击者,[d]代表防御者。
定义6:[T={T1,T2,…,T3}],并且对于任意的[i],[Ti] 不为空集,[Ti=(ti1,ti2,…,tin)],那么攻击者的策略集[Ta=(ta1,ta2,…,tan),]防御者的策略集[Td=(td1,td2,…,tdm)]。
定义7:[U]为参与者的效用函数的集合,[U=(U1,U2,…,Un)],[Ui=Ri-Ei],其中[R(Revenue)]为收益,[E(Expenditure)]为支出。
为简化攻击路径和防御路径效用值的计算,不考虑脆弱点之间的关联性等其他因素,设[α]为一个原子攻击,假定攻击者的攻击路径为[Wa=(α1,α2,…,αn)],防御者的防御路径为[Wd=(α1,α2,…,αm)],攻击路径效用值公式[U(Wa)=i=1nU(αi)] ,防御路径效用值公式[U(Wd)=i=1mU(αi)]。
由纳什均衡存在性定理可知,任意给定一个策略形式的三元组[G={(a,d),(Ta,Td),(Ua,Ud)}],攻防双方的策略分别为[Ta=(ta1,ta2,…,tan)]和[Td=(td1,td2,…,tdm),]通过效用值计算并生成博弈矩阵进行博弈便可得到其各自策略的概率分布[P(a)=(Pa1,Pa2,…,Pan),][P(d)=(Pd1,Pd2,…,Pdm)][0≤Pdi≤1,][0≤Pai≤1]且[i=1nPai=1,i=1nPdi=1]。算法如下:
输入:攻防双方,网络攻防的策略集
输出:可能攻击路径与最优防御策略
1.初始化[G={S,T,U}];
2.通过属性邻接矩阵运算得出所有可能路径,建立攻防双方策略集合:
[Ta=(ta1,ta2,…,tan),Td=(td1,td2,…,tdm);]
3.计算攻防所有路径效用[U(Wa)],[U(Wd)];
4.生成效用值博弈矩阵;
5.调用纳什均衡混合策略求解子算法;
6.得出可能的攻击路径与防御路径的[P(a)]和[P(d)],并进行分析,确定最优的防御策略;
7.算法结束
纳什均衡混合策略求解子算法如下:
輸入:攻防博弈效用矩阵
输出:纳什均衡解
1.Maximize [x]
2.[Subject to ?tj∈Tj]
3.[i=1mpiU(ti,tj)≥x]
4.[i=1mpi=1,0≤pi≤1]
该博弈算法关键是博弈模型的建立与求解,包括策略集建立,策略效用值的量化和纳什均衡值的求解。其时间复杂度主要取决于纳什均衡子算法的求解,可用非线性规划来求解,该模型的时间复杂度具有多项式级别,计算速度快,可以满足防御系统快速响应的需求。
2 实 验
2.1 实验环境
图3为民航某业务系统的网络拓扑图,本文在该环境模拟以下实验,验证了所提方法的简洁性和有效性。模拟环境包含1台Windows XP系统的攻击主机,6台服务器:Windows Server Web服务器、Windows Server MS SQL服务器、Windows Server FTP服务器、Linux Mail 服务器、DNS服务器、打印服务器。

图3 网络拓扑图
2.2 实验过程及结果

根据各主机之间可利用的脆弱点及脆弱点之间的关系,绘制属性攻击图,并简化,如图4所示。

图4 原始攻击图的简化(二)
根据简化后的攻击图可得到的属性邻接矩阵为:
通过查阅脆弱点信息,得到原子攻击信息表见表1。

表1 原子攻击信息表
据以往研究成果,利用各脆弱点进行攻击或防御的攻防双方的效用值信息如表2所示。
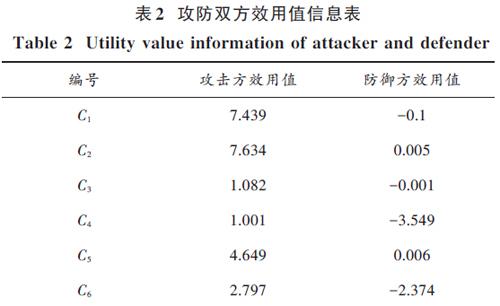
表2 攻防双方效用值信息表
研究人员通过对大量真实攻击数据的统计分析,现实的攻击中有效攻击路径长度一般不会超过3。因此本文不对较长的攻击路径进行研究。将属性邻接矩阵进行运算,并根据表2攻防双方的效用值信息表和第1.3节中求解攻防双方路径效用值的公式可以得到攻击路径的效用值信息表,如表3所示。

表3 攻防双方路径效用值信息表

表4为攻防双方的博弈矩阵。利用该模型求解表4的攻防效用矩阵,可以得到一个混合策略的纳什均衡[(0,1,0,0,0,0),(0,0.783 4,0,0,0.216 6,0)],即攻击者最可能选择C1→C2来进行攻击,防御者以0.783 4的概率选择C1→C2路径进行防御,以0.216 6的概率选择C1→C3→C5进行防御。因此,防御方最优防御策略应是以0.783 4的概率向Web服务器安装微软Bulletin MS13?004最新版本的安全更新,升级FTP服务器Serv?U至高版本;以0.216 6的概率向Web服务器安装微软Bulletin MS13?004最新版本的安全更新并安装微软IIS MS11?004安全更新。
3 结 论
本文提出一种新的网络风险控制的模型。用BFS算法简化攻击图,通过属性邻接矩阵的运算进一步降低对大规模攻击图分析的难度,增强了可视性,可快速得出任意两个节点之间的所有路径。最后通过博弈方法得出可能性较高的攻击路径和最佳防御策略,帮助网络管理员在有限的资源条件下有针对性地采取措施,加固关键节点。该模型具有多项式级别的时间复杂度,可快速响应防御系统的需求,极具实际意义。现实场景中攻防双方的动态博弈也是以后研究的重点。目前我国对风险控制的研究较少,该模型可以为以后网络风险管控体系的建立提供参考。
注:本文通讯作者为李跃凯。
参考文献
[1] Computer Security Institute. 15th annual 2010/2011 computer crime and security survey [J]. [2011?08?09]. https://www.docin.com/p?241701547.html.
[2] 陆余良,宋舜宏,程微微,等.网络攻击图生成方法分析[J].安徽大学学报(自然科学版),2010,34(4):23?30.
LU Yuliang, SONG Shunhong, CHENG Weiwei, et al. Analysis of the generation approaches to network attack graphs [J]. Journal of Anhui University (Natural sciences), 2010, 34(4): 23?30.
[3] 陈锋,张怡,苏金树,等.攻击图的两种形式化分析[J].软件学报,2010,21(4):838?848.
CHEN Feng, ZHANG Yi, SU Jinshu, et al. Two formal analysis of attack graphs [J]. Journal of software, 2010, 21(4): 838?848.
[4] OU X M, BOYER W F, MCQUEEN M A. A scalable approach to attack graph generation [C]// Proceedings of the 13th ACM Conference on Computer and Communications Security. Alexandria: ACM, 2006: 336?345.
[5] HOMER J, OU X M , SCHMIDT D. A sound and practical approach to quantifying security risk in enterprise networks [J/OL]. [2013?08?09]. http://people.cs.ksu.edu/~xou/publications/tr_homer_0809.pdf.
[6] NOEL S, JAJODIA S. Understanding complex network attack graphs through clustered adjacency matrices [C]// Proceedings of the 21st Annual Computer Security Applications Conference. Tucson: IEEE, 2006: 160?169.
[7] LYE K W, WING J M. Game strategies in network security [J]. International journal of information security, 2015, 4(1): 71?86.
[8] 姜伟.基于攻防博弈模型的主动防御关键技术研究[D].哈尔滨:哈尔滨工业大学,2010.
JIANG Wei. Research on the key technology of active defense based on offensive and defensive game model [D]. Harbin: Harbin Institute of Technology, 2010.
[9] 李庆朋,郑连清,张串绒,等.基于脆弱点利用关联的攻击图优化方法[J].计算机工程,2012,38(21):129?132.
LI Qingpeng, ZHENG Lianqing, ZHANG Chuanrong, et al. Optimization method for attack graph based on vulnerability exploit correlation [J]. Computer engineering, 2012, 38(21): 129?132.
[10] SHEYNER O M. Scenario graphs and attack graphs [D]. Pittsburgh: Carnegie Mellon University, 2004.
[11] WANG L, NOEL S, JAJODIA S. Minimum?cost network hardening using attack graphs [J]. Computer communications, 2006, 29(18): 3812?3824.
[12] 叶云,徐锡山,贾焰,等.基于攻击图的网络安全概率计算方法[J].计算机学报,2010,33(10):1987?1996.
YE Yun, XU Xishan, JIA Yan, et al. An attack graph?based probabilistic computing approach of network security [J]. Chinese journal of computers, 2010, 33(10): 1987?1996.
[13] 苏婷婷,潘晓中,肖海燕,等.基于属性邻接矩阵的攻击图表示方法研究[J].电子与信息学报,2012,34(7):1744?1747.
SU Tingting, PAN Xiaozhong, XIAO Haiyan, et al. Research on attack graph based on attribute adjacency matrix [J]. Journal of electronics & information technology, 2012, 34(7): 1744?1747.
[14] RITCHEY R, O′BERRY B, NOEL S. Representing TCP/IP connectivity for topological analysis of network security [C]// Proceedings of the 18th Annual Computer Security Applications Conference. Las Vegas: IEEE, 2012: 156?165.
