模块化多电平换流器等效模型的研究

高志鹏 袁旭峰 胡实 张朝学 刘隽恺 谈竹奎

摘  要： 模块化多电平换流器（MMC）在仿真过程中随着电平数量的增加导致仿真效率降低。针对这一问题，通过研究现阶段相对成熟的4种等效模型，即基于戴维南等效、基于受控电压源等效、基于平均值等效以及基于开关函数等效的详细等效模型，并进一步分析上述4种等效的数学建模、等效思想以及每个模型的特性功能，进而从功能以及应用范围的角度进一步对其进行分类讨论，并划定分类标准。最后针对4种模型不同的特性、优缺点分别进行对比，最终得到一个可广泛适用于多种情况的对比结果，为选取模型提供标准。

关键词： 模块化多电平换流器; 仿真效率; 数学建模; 等效模型; 分类讨论; 对比分析

中图分类号： TN624?34; TM46                  文献标识码： A                    文章编号： 1004?373X（2019）10?0060?07

Research on equivalent model of modular multilevel converter

GAO Zhipeng1， YUAN Xufeng1， HU Shi1， ZHANG Chaoxue1， LIU Junkai1， TAN Zhukui2

（1. School of Electrical Engineering， Guizhou University， Guiyang 550025， China; 2. Guizhou Electric Power Research Institute， Guiyang 550002， China）

Abstract： The simulation efficiency of the modular multilevel converter （MMC） will be reduced with the increase of the level quantity during its simulation process. Therefore， in the current stage， four relatively?mature equivalent models based on Thevenin equivalence， controlled voltage source equivalence， average value equivalence， and switch function detailed equivalence are studied. The mathematical modeling， equivalent thoughts， and feature functions of the above four equivalent models are further analyzed. Classification of the four models is further discussed in the aspects of function and application range， and the classification criteria are determined. The different characteristics， advantages and disadvantages of the four models are compared. The comparison result widely applicable to various situations is obtained， which can provide a criterion for model selection.

Keywords： modular multilevel converter; simulation efficiency; mathematical modeling; equivalent model; classification discussion; comparative analysis

0  引  言

随着电力电子领域的深入发展，柔性直流输电技术（VSC?HVDC）的应用日益推广[1]，尤其在远距离大容量输电以及交流电网异步互联等场合中应用广泛。目前，世界范围内在建的各大柔性直流输电工程大多采用模块化多电平换流器（Modular Multilevel Converter，MMC）[2?4]。MMC相较于传统的两电平结构具有得天独厚的优点，从工程实践来看，由于电压和容量扩展便捷、无需器件串联等优点，以MMC结构为基础的换流器方案更适合直流输电[5?6]。

随着HVDC向多端互联、高电压、大功率的方向应用，MMC拓扑中单个桥臂所需要串联的子模块（Sub?Module，SM）的数量与日俱增[7]。如我国舟山的无端柔性直流输电示范工程共包含超过8 000个子模块[8]，使得在研究过程中，传统的PSCAD/EMTDC等电磁暂态仿真系统很难高效仿真，因为如此大规模的模型，以20 [μs]步长仿真时长5 s的系统，需要数月的时间[9?11]，严重制约了MMC技术的研究与应用。

为实现MMC直流系统的高效仿真，国内外学者开展了大量的研究。从根本上来看，大规模MMC仿真时间太长是因为在实际拓扑中，开关器件的数量过于庞大，并且每时每刻都在发生着改变，这增加了软件求取系统矩阵的时间[12?13]。因此，研究MMC的等效模型，简化开关器件，成为了一个热门的研究方向。基于此，文献[9]最早建立MMC子模块的戴维南等效模型，文献[8]在此基础上做了进一步优化，文献[14]则开展了可行性验证并细化了元件等值计算模型;文献[15?16]提出多种平均值等效模型，分别从MMC解析模型，将桥臂等效受控电压源以及从数学上等效详细开关模型等多个角度建立平均值模型;文献[17]提出一种能仿真两电平VSC与MMC直流故障的通用平均值建模;文献[10?11]将MMC等效为受控式电压源进行等效。本文将对国内外现有的多种等效模型进行综合列举，详细分析，并进行分类，最后进行对比，得出不同等效模型的优缺点以及不同的应用范围，以期达到分类有致、对比鲜明。

1  MMC及其子模块拓扑

三相模块化多电平换流器的拓扑结构如图1所示，一个换流器由6个桥臂构成，每相的上下两个桥臂构成一个相单元，每个桥臂由一个电抗器和[N]个子模块串联而成。

图1  三相MMC拓扑结构

子模块采用半H桥结构，虽然这种拓扑结构不具备有效的直流故障穿越能力，但是相比于H桥和箝位子模块，半H桥SM所投入的电力电子器件更少，且经济性更好，是现阶段的主流选择[18?19]。

2  MMC暂态仿真等效模型分类及分析

本文将各类电磁暂态等效模型从仿真精细程度出发分为两种大类，分别是精确仿真模型以及简单仿真模型。其中，精确仿真模型可以精确仿真每个子模块的充放电过程;而简单仿真模型虽然无法仿真子模块的充放电过程，但具体计算复杂程度不随电平的变化而变化，具有一定的稳定性，仿真过程更加高效，适用于超大规模的MMC多端网络的仿真实现。MMC等效模型分类如图2所示。

图2  MMC等效模型分类

2.1  基于戴维南等效的MMC模型

基于戴维南等效的MMC模型，其基本思想是从每个子模块出发，对每个子模块进行数学分析以及元件离散化表达等一系列等效后，建立单个子模块的戴维南等效模型，进而在此基础上进行代数叠加从而得到整个桥臂的戴維南等效。

MMC子模块的拓扑图如图3所示，MMC子模块戴维南等效电路如图4所示。图3中，IGBT（TI）及反并联二极管（D1）可视为一个开关集合，等效为一个可变电阻[15]。当开关导通时可视作[RON]，即一个非常小的电阻;当开关关断时视为[ROFF]，即一个非常大的电阻。用[R1]，[R2]等效两个开关集合，其阻值取值根据相对应的开关状态，而开关状态由MMC控制器决定。

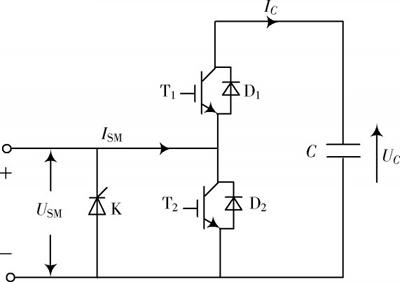
图3  MMC子模块拓扑图

图4  MMC子模块戴维南等效电路

电容的等效采用离散化的思想，文献[9]中采用应用广泛的梯形积分法（Trapezoidal Rule，TR）进行离散，等效为一个等效电阻[RC]和等效电压[UCEQ]，其取值都是时间的函数，根据梯形积分法得：[UCt=1C0tICtdT≈UCt-ΔT+                 1CICt-ΔT+ICt2ΔT] （1）

将式（1）进一步改写：

[UCt=RC·ICt+UCEQt-ΔT] （2）

式中：

[RC=ΔT2C] （3）

[UCEQt-ΔT=ΔT2CICt-ΔT+UCt-ΔT] （4）

由式（3）可知，电容的等效电阻仅与仿真步长和电容值有关。由式（4）可知，电容[C]的上一时刻电压源与[t-ΔT]时刻的电容电压以及此时流经电容的电流大小有关。电容电流[ICt]为：

[ICt=ISMtR2-UCEQt-ΔTR1+R2+R3] （5）

[RSMEQt]与[USMEQt-ΔT]为：

[RSMEQt=R21-R2R1+R2+R3] （6）

[USMEQt-Δt=R2R1+R2+R3UCEQt-Δt] （7）

式中，[R1]，[R2]为两个状态的变量。

将单个桥臂上N个子模块都进行上述戴维南等效，并进行叠加可以得到整个桥臂的戴维南等效电路如图5所示。

图5  MMC桥臂戴维南等效电路

图中：[Uarm]为桥臂输出电压;[Iarm]为桥臂电流;[UC]和[TSM]为桥臂输出的[N]个子模块电容电压以及控制模块输入桥臂的子模块触发信号。

[Uarmt=iNUSMi（t）=IarmtRarmeqt+Uarmeqt] （8）

式中：

[Uarmeq（t）=i=1NUSMEQi（t-Δt）Rarmeq（t）=i=1NRSMEQi（t）] （9）

式中，[USMEQi]，[RSMEQi]分别表示第[i]个子模块的戴维南等效电压和电阻。

2.2  基于电压源等效的MMC等效模型

基于电压源等效是通过数学建模将整个桥臂等效为n个数字计算的详细模块（Numerical Calculation Detailed Module，NCDM）以及受控电压源[20]，通过计算和测量来获得相应的数据并进行分析。其基本思想是将子模块等效为受控电压源，使桥臂与子模块实现电气隔离，部分保留了详细模型的开关器件的信息，易于实现。

在图3中，[K]的作用是当直流母线发生双极短路时，晶闸管导通保护[IGBT]和二极管不被损坏。

电容接入，子模块输出电容电压;电容退出，子模块输出为0。其关系表达式为：

[USM=SCUC+Ucon，SC=1，0] （10）

式中：[Ucon]为半导体开关器件导通压降;[SC]为子模块的接入状态，电容接入取值为1，电容退出取值为0。IGBT的特性可表示为：

[Ucon=R0Icon+U0] （11）

式中：[R0]为半导体器件正向导通电阻;[U0]为 IGBT的擎住电压或者反并联二极管的门槛电压;[Icon]为流过半导体开关器件的电流。这里[R0]取半导体材料导通电阻[Ron]，[U0]取正向压降[UFD]。

[Ucon=Ron，diode?IRM+UFD，diode，  IRM>0， SC=1 Ron，IGBT?IRM-UFD，IGBT，  IRM<0， SC=1 Ron，IGBT?IRM+UFD，IGBT，  IRM>0， SC=0Ron，diode?IRM-UFD，diode，  IRM<0， SC=0] （12）

式中，diode与IGBT分别表示diode型与IGBT型半导体器件。根据电容充放电原理得：

[UC（t+ΔT）=UC（t）+SCCtt+ΔtIRM（τ）dτ] （13）

式中，[ΔT]，[t]分别为仿真步长与仿真起始时间。

整个桥臂的输出电压[Uarm] 由串联的所有子模块叠加而得：

[Uarm=i=1NUSMi=i=1N（Uconi+UCiSCi）] （14）

式中，[UCi] 表示桥臂中第[i]个子模块的电容电压。

基于上述数学分析，建立数学计算模型（NCDM）。整个基于受控电压源的MMC等效模型的基本思路可归纳如下：控制模块即电压调制计算子模块个数[Non]，以及所测得的桥臂电流[Iarm]，通过均压控制计算得到的子模块开关指令集合[ST[N]]。将[ST[N]]与[Iarm]共同输入NCDM模块，计算得到桥臂输出电压[Uarm]。通过触发信号判断电容的接入状态，经式（13）得到[N]个子模块的电容电压集合[UCN]反馈回到均压控制。

开关与晶体管的作用是模拟MMC闭锁功能，当有直流双极短路故障时，等效子模块的受控电压源将被开关从电路中断开，同时触发晶闸管模拟子模块中[K]的闭锁功能[21]。整个详细模型图如图6所示。

图6  基于受控电压源MMC等效模型

2.3  MMC平均值等效模型

无论是戴维南等效，还是电压源等效，都是从MMC内部子模块的投切进行等效。随着子模块数量的增加，计算和仿真难度也逐步提升，其仿真速度就很难满足要求。文献[20]介绍的MMC平均值模型虽然无法模拟子模块充、放电特性，但是计算复杂度不随电平的变化而变化，在对大规模交、直混合系统的分析中具有独特的优势。平均值等效的基本思想是将整个SM子模块用受控电压或者电流源代替，具体为交流侧由6个受控电压源代替，直流侧由一个受控源和一个等效电容代替，其结构如图7所示[15]。

交流侧的模型如图7a）所示，上下桥臂受控源电压值为：

[Uarm_up=ModUdc2-econUjUCAVUCAV] （15）

[Uarm_dn=ModUdc2+econUjUCAVUCAV] （16）

式中：[UCAV]为子模块电容电压平均值，在平均值模型中为[UdcN];[econUj]为[j]相交流调制波;[Mod[]] 为取整函数，代表MMC调制策略[22]。

图7  平均值模型

直流侧的模型如图7b）所示，其推导由功率平衡理论得到，[I′dc]表示从交流侧流入MMC的直流等效电流。

[I′dc=j=a，b，ceconUjijUdc] （17）

电流[Iloss]表示MMC换流器的损耗：

[Iloss=RlossI′dc2Udc] （18）

[I′dc]减去[Iloss]得到最终流入外部直流网络的电流[Idc]：

[Idc=I′dc-Iloss] （19）

式中，[Rloss]是MMC等效损耗电阻，既有开关也有电阻性损耗。

由能量平衡理论可知，MMC平均值模型中惟一的直流侧等效电容[CAVM]计算公式为：

[CAVM=6CN] （20）

式中，C为子模块中电容值

以上为MMC平均值模型的基本介绍，其实质是利用受控源实现交、直流的电气解耦，思路上同基于受控源的等效模型是一致的，但是平均值模型不考慮子模块的等效，无法模拟单个子模块的充、放电过程。

2.4  MMC桥臂开关函数模型

开关函数模型中每条MMC桥臂均采用开关函数的思想来进行替代。文献[12，23?24]介绍了半桥以及混合子模块桥臂开关函数模型的数学建模，本文仅介绍半桥MMC的不同工况，用开关函数进行数学代替。首先设定开关函数[Si]，当SM子模块退出时，取值为0，当SM子模块投入时，取值为1。对于每个SM子模块：

[USMi=SiUCi] （21）

[iCi=Siiarm] （22）

假定每个桥臂的电容电压是平衡的，电容电压的平均值相同。在这种情况下，忽视电容之间的电压差，则可以得到：

[UC1=UC2=…=UCi=UCtotN] （23）

式中，[UCtot]代表单个桥臂所有电容的和。当单个桥臂的子模块SM个数增加，或者当电容电压的波动幅度减少时，式（23）的假设就更接近准确值，仿真也就更加精确。所以，这种等效在大规模的MMC仿真中更加适用。此外，每个桥臂的等效电容[Carm=CN] 。

定义单个桥臂的开关函数如下：

[1Ni=1NSi=sn] （24）

考虑每个SM的损耗（[RON]），每个桥臂在不同的工作状态时的开关函数为：

[Uarm=snUCtot+（NRON）iarm] （25）

[iCtot=sniarm] （26）

此外，因为半桥子模块电压不可逆，为了避免出现负电压，在等效电容器旁并联一个二极管D，如图8所示。当所有的子模块处于闭锁状态时，每个MMC桥臂可以简单地等效为半桥二极管与等效电容相连。

通过将整个桥臂等效为开关函数模型，不再需要任何其他电力电子器件，这意味着每个臂上的电容电压的平衡控制和冗余[25]SM的影响不能用这种方法来研究。但是环流和线性阻抗损耗可以在这个模型中体现出来。此外，MMC每个桥臂上交、直流间的能量传递也得以体现，这对于基于内部MMC能量平衡的控制系统策略是很有用的[26]。

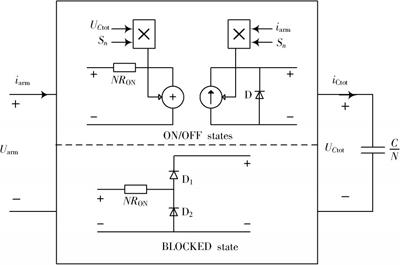
图8  MMC桥臂开关函数模型

3  不同类型MMC等效模型的对比

在现阶段的研究中，针对仿真对象的不同类型和不同需求，选取正确并最具有效率的等效模型是减少研究和仿真成本的首要步骤。基于此，本文将4种类型的适用范围及优缺点进行总结整理，得到一个相对清晰明了的对比结果见表1。若仿真规模相对较小，并需要对子模块内部充、放电等有详细仿真，则选取精确仿真模型。基于受控源MMC等效仿真是相对最为容易实现的办法，但是仍需采用与详细模型相同的调制以及均压算法。相比而言，基于戴维南等效的仿真方法，可以进一步优化相关调制及均压算法，使仿真效率进一步提高。

若仿真对象为超大规模MMC系统，就可选用简单仿真模型。但是，平均值模型因为结构过于简单，其仿真暂态稳态的适用性是需要进一步研究的，很大程度上，这种仿真类型的准确性都是建立在子模块数量足够大的基础上。除此以外，基于开关函数的等效模型因为完全舍弃了电力电子器件，因此控制侧面的均压以及冗余控制等相关研究就无法进行。基于上述分析，通过表1可以进行对比和选取。

4  结  语

本文在现阶段对MMC等效模型研究基础上，对多而杂乱的不同模型进行选择并分类，选取4种相对研究成熟的MMC等效模型将其分为两大类：精确等效模型以及简单等效模型。并相对应的每种分类下介绍两种等效，就其具体的原理、基本思想以及数学建模进行了详细的介绍，并给出了不同的适用范围。

在分析了不同模型的优缺点后，基于这4种模型，本文将其归于一处以表格的形式罗列出优缺点以及相对应的适用范围，力求做到清晰明了、对比有致。根据仿真对象、研究深度、研究内容进行不同的筛选，选取最适合的等效对象进行建模仿真，省去很多盲目的工作，为研究提供一个前置的便利条件。在此基础上，分别研究各类模型的特性，就有了相对清晰的方向，大大减少了工作量。

参考文献

[1] 杨燕，林勇，徐蔚，等.乌东德多端直流输电对广东电网安全稳定的影响[J].广东电力，2017，30（11）：44?50.

YANG Yan， LIN Yong， XU Wei， et al. Influence of Wudongde multi?terminal HVDC on security and stability of Guangdong power grid [J]. Guangdong electric power， 2017， 30（11）： 44?50.

[2] 杨晓峰，林智钦，郑琼林，等.模块组合多电平变换器的研究综述[J].中国电机工程学报，2013，33（6）：1?15.

YANG Xiaofeng， LIN Zhiqin， ZHENG Qionglin， et al. A review of modular multilevel converters [J]. Proceedings of the CSEE， 2013， 33（6）： 1?15.

[3] 孔明，汤广福，贺之渊.子模块混合型 MMC?HVDC直流故障穿越控制策略[J].中國电机工程学报，2014，34（30）：5343?5351.

KONG Ming， TANG Guangfu， HE Zhiyuan. A DC fault ride?through strategy for cell?hybrid modular multilevel converter based HVDC transmission systems [J]. Proceedings of the CSEE， 2014， 34（30）： 5343?5351.

[4] XUE Yinglin， XU Zheng， TANG Geng. Self?start control with grouping sequentially precharge for the C?MMC?based HVDC system [J]. IEEE transactions on power delivery， 2014， 29（1）： 187?198.

[5] LESNICAR A， MARQUARDT R. An innovative modular multilevel converter topology suitable for a wide power range [C]// Proceedings of IEEE Power Tech Conference. Bologna： IEEE， 2003： 1?6.

[6] ZHANG L， ZOU Y， YU J， et al. Modeling， control， and protection of modular multilevel converter?based multi?terminal HVDC systems： a review [J]. CSEE journal of power and energy systems， 2017， 3（4）： 340?352.

[7] TU Qingrui， XU Zheng. Impact of sampling frequency on harmonic distortion for modular multilevel converter [J]. IEEE transactions on power delivery， 2011， 26（1）： 298?306.

[8] 许建中，赵成勇，Aniruddha M.Gole.模块化多电平换流器戴维南等效整体建模方法[J].中国电机工程学报，2015，35（8）：1919?1929.

XU Jianzhong， ZHAO Chengyong， GOLE A M. Research on the Thévenin′s equivalent based integral modelling method of the modular multilevel converter （MMC） [J]. Proceedings of the CSEE， 2015， 35（8）： 1919?1929.

[9] GNANARATHNA U N， GOLE A M， JAYASINGHE R P. Efficient modeling of modular multilevel HVDC converters （MMC） on electromagnetic transient simulation programs [J]. IEEE transactions on power delivery， 2011， 26（1）： 316?324.

[10] 许建中，赵成勇，刘文静.超大规模 MMC 电磁暂态仿真提速模型[J].中国电机工程学报，2013，33（10）：114?120.

XU Jianzhong， ZHAO Chengyong， LIU Wenjing. Accelerated model of ultra?large scale MMC in Electromagnetic transient simulations [J]. Proceedings of the CSEE， 2013， 33（10）： 114?120.

[11] XU Jianzhong， ZHAO Chengyong， LIU Wenjing， et al. Accelerated model of modular multilevel converters in PSCAD/EMTDC [J]. IEEE transactions on power delivery， 2013， 28（1）： 129?136.

[12] 徐政.柔性直流输电系统[M].北京：机械工业出版社，2013.

XU Zheng. Flexible DC power transmission system [M]. Beijing： China Machine Press， 2013.

[13] Manitoba HVDC Research Center. PSCAD： power systems computer aided design [EB/OL]. [2013?12?17]. http：//www.doc88.com/p?7028074238845.html.

[14] 周阳，常非.MMC电磁暂态快速仿真模型[J].电力系统保护与控制，2016，44（1）：1?8.

ZHOU Yang， CHANG Fei. Quick model of MMC in electromagnetic transient simulations [J]. Power system protection and control， 2016， 44（1）： 1?8.

[15] PERALTA J， SAAD H， DENNETIERE S， et al. Detailed and averaged models for a 401?level MMC–HVDC system [J]. IEEE transactions on power delivery， 2012， 27（3）： 1501?1508.

[16] GNANARATHNA U N， GOLE A M，  JAYASINGHE R P. Efficient modeling of modular multilevel HVDC converters （MMC） on electromagnetic transient simulation programs [J]. IEEE transactions on power delivery， 2011， 26（1）： 316?324.

[17] 周诗嘉，林卫星，姚良忠，等.两电平VSC与MMC通用型平均值仿真模型[J].电力系统自动化，2015，39（12）：138?145.

ZHOU Shijia， LIN Weixing， YAO Liangzhong， et al. Generic averaged value models for two?level VSC and MMC [J]. Automation of electric power systems， 2015， 39（12）： 138?145.

[18] 管敏渊，徐政.模块化多电平换流器的快速电磁暂态仿真方法[J].电力自动化设备，2012，32（6）：36?40.

GUAN Minyuan， XU Zheng. Fast electro?magnetic transient simulation method for modular multilevel converter [J]. Electric power automation equipment， 2012， 32（6）： 36?40.

[19] 韦延方，卫志农，孙国强，等.适用于电压源换流器型高压直流输电的模块化多电平换流器最新研究进展[J].高电压技术，2012，38（5）：1243?1252.

WEI Yanfang， WEI Zhinong， SUN Guoqiang， et al. New prospects of modular multilevel converter applied to voltage source converter high voltage direct current transmission [J]. High voltage engineering， 2012， 38（5）： 1243?1252.

[20] 喻锋，王西田，林卫星，等.模块化多电平换流器快速电磁暂态仿真模型[J].电网技术，2015，39（1）：257?263.

YU Feng， WANG Xitian， LIN Weixing， et al. Fast electromagnetic transient simulation models of modular multilevel converter [J]. Power system technology， 2015， 39（1）： 257?263.

[21] SAAD H， PERALTA J， DENNETI?RE S， et al. Dynamic averaged and simplified models for MMC?based HVDC transmission systems [J]. IEEE transactions on power delivery， 2013， 28（3）： 1723?1730.

[22] 许建中.模块化多电平换流器电磁暂态高效建模方法研究[D].保定：华北电力大学，2014.

XU Jianzhong. Research on the electromagnetic transient efficient modelling method of modular multilevel converter [D]. Baoding： North China Electric Power University， 2014.

[23] SAAD H， DENNETI?RE S， MAHSEREDJIAN J， et al. Modular multilevel converter models for electromagnetic transients [J]. IEEE transactions on power delivery， 2014， 29（3）： 1481?1489.

[24] LI R， XU L， GUO D. Accelerated switching function model of hybrid MMCs for HVDC system simulation [J]. IET power electronics， 2017， 10（15）： 2199?2207.

[25] GEMMELL B， DORN J， RETZMANN D， et al. Prospects of multilevel VSC technologies for power transmission [C]// Proceedings of IEEE/PES Transmission and Distribution Conference and Exposition. Chicago： IEEE， 2008： 1?16.

[26] M?NCH P， G?RGES D， IZ?K M， et al. Integrated current control， energy control and energy balancing of modular multilevel converters [C]// Proceedings of 36th Annual Conference on IEEE Industrial Electronics Society. Glendale： IEEE， 2010： 150?155.