长江经济带包容性绿色增长的测度与区域差异分析
2019-06-20王宇昕余兴厚黄玲
王宇昕 余兴厚 黄玲

摘 要:通过理论分析,构建长江经济带包容性绿色增长评价体系,选用熵权TOPSIS法评价长江经济带110个城市的包容性绿色增长水平。运用基尼系数、泰尔指数和对数离差均值等差异性指标测度了长江经济带各区域内包容性绿色增长的均等化程度,并引入σ收敛模型、绝对β收敛模型和条件β收敛模型检验其收敛性特征。结果显示:长江经济带整体包容性绿色增长水平以2013年为转折点,呈现先递减后上升的趋势;经济发展和生态环境保护扮演着长江经济带整体包容性绿色增长中最重要的两个角色,绿色生产与资源消费的重要性日益增强;区域差异以2013年为拐点,呈现先上升后下降的“倒U”型变化趋势;各区域包容性绿色增长存在着显著的收敛性,上、中游地区β收敛系数的绝对值明显大于下游地区,存在着上、中游地区对下游地区的“追赶效应”;技术创新和人力资本水平提升对各区域包容性绿色增长的收敛具有显著正向影响。
关键词:包容性绿色增长;综合评价;区域差异;收敛性分析;长江经济带
文章编号:2095-5960(2019)03-0089-10;中图分类号:F0622;文献标识码:A
一、引言和文献综述
继2012年联合国可持续发展大会提出“可持续发展和消除贫困背景下的绿色经济”之后,包容性绿色增长的发展理念引起了全世界的广泛关注。长江经济带作为我国最具潜力的新兴增长极之一,如何进一步提升长江经济带包容性绿色增长水平成为推动长江经济带高质量发展的关键。本文通过构建长江经济带包容性绿色增长评价体系,运用熵权TOPSIS法客观评价长江经济带110个城市包容性绿色增长水平,运用基尼系数、泰尔指数和对数离差均值等差异性指标测度了长江经济带各区域内包容性绿色增长的均等化程度,并引入σ收敛模型、绝对β收敛模型和条件β收敛模型检验其收敛性特征,最后根据实证研究结论提出对策建议。
目前学术界关于包容性绿色增长的文献研究主要围绕着包容性绿色增长理论的内涵和包容性绿色增长的测度两个方面。在理论内涵的方面,World Bank(2012)认为只有同时具备社会包容性和绿色性,才能实现经济长期的可持续增长[1];OECD(2012)认为包容性绿色增长为可持续发展提供了一种更易操作的方法[2];张晓颖(2014)认为包容性绿色增长更加注重人在经济、社会发展和自然环境中的作用与地位,特别是对穷人等弱势群体的包容[3];张苟嘉(2015)认为包容性绿色增长是建立在生态环境保护基础上的一种共享式增长模式[4];在测度方面,杨雪星(2014)分别从包容性经济、绿色经济和绿色经济对社会发展的驱动力三个维度,对G20国家2010年包容性绿色增长指数进行评价,测算结果显示我国位于综合排名第四位[5];徐宝亮和钟海燕(2015)从经济增长、机会公平、成果共享和资源环境等4个一级指标,8个二级指标和19个三级指标,运用因子分析法对我国2001—2011年绿色包容性增长进行动态分析[6];吴武林和周小亮(2018)基于经济增长的收入效应、社会效应和环境效应三个维度,运用熵权法对我国30个省份1999—2015年包容性绿色增长指数进行了测算,发现省际不平衡、不协调和不充分的现象严重,其中东部地区的整体水平高于中西部地区[7];胡书芳和马宪法(2017)基于浙江省绿色发展的现状,从经济、环境和社会三个方面构建城市绿色发展指标,运用灰色关联分析法测量出浙江省内各城市在2015年的绿色发展指数[8]。也有一些学者研究了长江经济带如何实现协调发展和绿色增长的问题[9][10][11]。
综合来看,虽然国内外学者围绕包容性绿色增长做了大量的理论分析和实证研究,取得较为丰硕的成果,但笔者认为还存在着以下几方面的不足:(1)在评价指标体系中,指标的内涵与外延缺乏清晰的认识,指标的选取较为主观,指标的构建结构较为单薄;(2)研究对象主要还停留在省级层面,忽略了各省内部包容性绿色增长水平的差異性问题;(3)截面数据的静态分析较多,而面板数据的动态比较较少。鉴于此,本文基于包容性绿色增长的理论研究,借鉴现有学者构建的绿色发展指标体系,从长江经济带的发展现状出发,设计出长江经济带包容性绿色增长的评价指标体系,运用熵权TOPSIS法对2011—2016年长江经济带110个城市包容性绿色增长水平进行测度,依据测度结果,采用基尼系数、泰尔指数和对数离差均值等差异性指标测度了各区域内与区域间的包容性绿色增长均等化程度,并引入σ收敛模型、绝对β收敛模型和条件β收敛模型检验其收敛性特征。
二、长江经济带包容性绿色增长的评价指标体系构建
(一)构建思路
当前学术界对包容性绿色增长的内涵界定尚未形成统一认识。从发展经济学范畴,可将包容性绿色增长归纳为一种强调增强社会包容性和提升人与自然和谐共生性的可持续发展方式;从福利经济学范畴,可将其理解为以增进当代人和后代人福祉为根本目标的经济增长模式。然而,到目前为止,现有文献还设有对包容性绿色增长的外延形成清晰的界定,这不得不说是一大遗憾。梳理现有研究,笔者将包容性绿色增长界定为以增进民生福祉为根本目的,以生态资源环境为硬约束的,经济、社会与自然三大系统协调耦合的高质量经济发展方式。本文借鉴周小亮和吴武林(2018)[7]的研究成果,参照2016年国家发改委印发的《绿色发展指标体系》,分别从经济发展、社会公平、绿色生产与消费、生态环境保护四个维度对长江经济带包容性绿色增长的内涵进行概括。
(二)指标选取
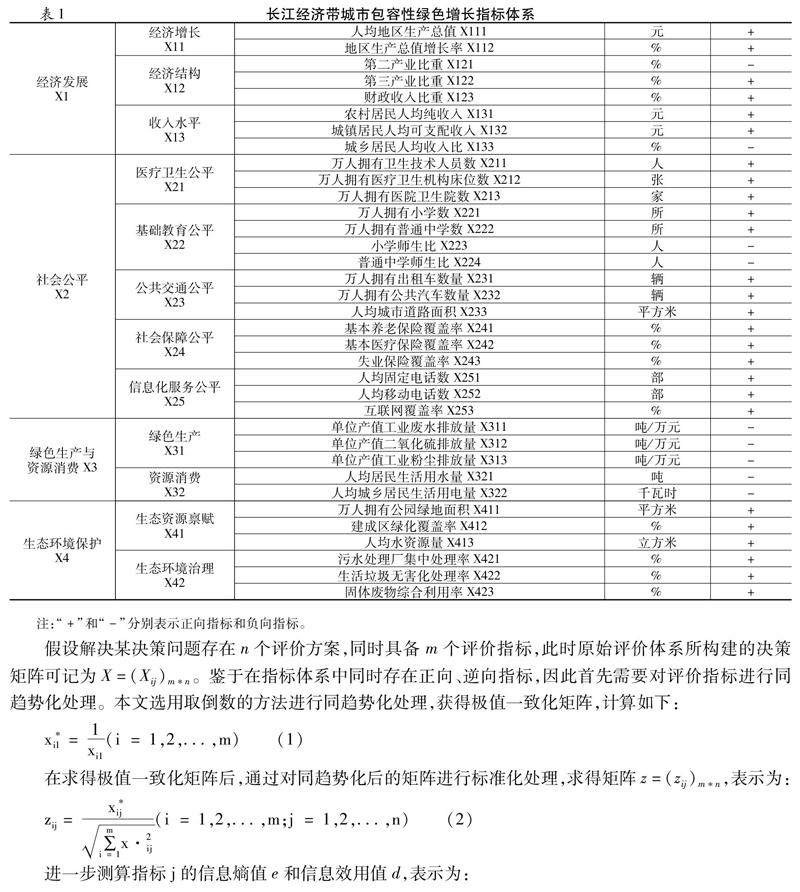
依据长江经济带包容性绿色增长的内涵、外延和关键内容,依次构建4个一级指标、12个二级指标和35个三级指标,具体详见表1。其中一级指标主要沿用周小亮和吴武林(2018)[7]的研究成果,分别是经济发展、社会公平、绿色生产与消费以及生态环境保护四部分;本文设计的二级指标与周小亮和吴武林的不同之处在于从经济增长、经济结构和收入水平三个方面来测度经济发展,此外还在社会公平中引入了信息化服务公平和公共交通公平等内容;本文与周小亮和吴武林(2018)[7]所构建的指标差异最大的在三级指标部分,这也是本文的创新所在。鉴于本文是测量长江经济带市域的包容性绿色增长水平,因此在指标的选取上应该充分考虑数据的可及性。如在社会公平的基本公共服务方面,借鉴余兴厚和熊兴(2018)[12]的资源禀赋和主体认知的思路,分别从机会、过程和结果的视角将社会公平的三级指标进一步丰富和完善。在基础教育公平方面包含万人拥有小学数、万人拥有普通中学数、小学师生比、普通中学师生比4个指标;在公共交通公平领域包含万人拥有出租车数量、万人拥有公共汽车数量、人均城市道路面积3个指标;在信息化服务公平领域包含人均固定电话数、人均移动电话数和互联网覆盖率3个指标。
三、研究方法及模型假设
本文选用熵权TOPSIS对长江经济带110个城市①的包容性绿色增长水平进行测算,并在测算结果的基础上运用差异性指标分别对长江经济带整体和各区域内、区域间包容性绿色增长均等化水平进行测度,最后构建收敛模型探究其收敛特征。本文研究时期为2011—2016年,相关数据来源于历年《中国城市统计年鉴》、《中国区域统计年鉴》和《各省市统计年鉴》。①①鉴于阿坝藏族羌族自治州、凉山彝族自治州等16个少数民族自治州的部分统计数据不完整,本文的测算分析不考虑少数民族自治州。
(一)熵权TOPSIS法
TOPSIS法作为一种常用的评价方法,其主要思想是根据评价对象和其理想化目标的距离进行比较排序(Olson,2004)[13]。但由于评价的环境或自身条件的变化通常会导致最优解与最劣解发生变化,使得评价结果发生偏差,因此我们引入熵值法参照指标的变异程度明确各评价指标的客观权重,可以有效减少变动因素的影响,使得所计算出的评价结果更具有精确性。
假设解决某决策问题存在n个评价方案,同时具备m个评价指标,此时原始评价体系所构建的决策矩阵可记为X=(Xij)m*n。鉴于在指标体系中同时存在正向、逆向指标,因此首先需要对评价指标进行同趋势化处理。本文选用取倒数的方法进行同趋势化处理,获得极值一致化矩阵,计算如下:
若Ci值越接近于1,则表示该评价对象越接近于最优评价水平;反之,越偏离最优评价水平。
(二)基尼系数、泰尔指数与对数离差均值
泰尔指数、基尼系数和对数离差均值作为常用的测量差异性的统计指标,其间具有一定的互补性。其中,泰尔指数和对数离差均值分别对上层部分和底层部分的差异变化比较敏感,而基尼系数则对中间部分的差异变化比较敏感。基尼系数(GINI)、泰尔指数(GE1)和对数离差均值(GE0)的计算公式分别表示如下:
式(12)、(13)和(14)中,n代表样本个数;ei表示将包容性绿色增长水平按照由小至大的顺序依次排列后第i个城市的包容性绿色增长水平;ue表示样本总体包容性绿色增长水平的均值。另外,通过对泰尔指数与对数离差均值分解,可进一步计算出组间和组内的差异程度。
(三)收敛模型
1σ收敛模型。本文的σ收敛是指长江经济带不同地区包容性绿色增长水平的差异性或变异性随着时间所表现出的降低趋势。借鉴周小亮和吴武林(2018)[11]、刘明和王思文(2018)[14]等文献的做法,构造包容性绿色增长的σ收敛模型为:
2绝对β收敛模型。绝对β收敛的概念最早来源于Baumol于1986年所提出的经济趋同理论。本文的β收敛是指长江经济带中包容性绿色增长水平相对较低的城市比包容性绿色增长水平相对较高的城市具有更快的增长速度,即在不考虑外在因素下,包容性绿色增长的期初水平与增长速度具有负相关性。借鉴王许亮和王恕立(2018)[15]文献的思路,本文构造的包容性绿色增长绝对β收敛模型①①本文的绝对β收敛检验采用截面模型检验。
②本文的条件β收敛检验采用固定效应面板模型检验。 为:
3条件β收敛模型。本文的条件β收敛是指在考虑到各城市的外在影响因素的存在差异性下,各城市的包容性绿色增长最后都会收敛到各自稳定的状态水平。借鉴滕泽伟等(2017)[16]文献的做法,本文的构造包容性绿色增长条件β收敛模型②为:
式(17)中的X代表外在影响因素变量的矩阵,λ代表相关系数矩阵,其余变量的含义与式(16)相同。若其值显著为负,则表明这n个城市存在条件β收敛;反之,则不存在条件β收敛。
四、实证结果与分析
(一)包容性綠色增长综合评价
根据上述熵权TOPSIS法测算2011—2016年长江经济带110个市域包容性绿色增长水平的综合评价得分,使用逐级累计求权处理方法确定各指标的权重,即首先通过对三级指标进行赋权,求出二级指标的得分;再对二级指标赋权进而求出一级指标得分,在此基础上通过熵权法对一级指标进行赋值,得到一级指标的权重矩阵,最后使用TOPSIS法计算出各市包容性绿色增长水平的综合得分。各年的一级指标权重与长江经济带110个市域包容性绿色增长水平的描述性统计结果分别见表2、表3。
从表2各年的一级指标权重值和变化趋势来看,经济发展的平均权重在包容性绿色增长中的比重最大,且整体上呈平稳递增趋势,从2011年的03122上升至2016年的03437;其次是生态环境保护,虽然在2012—2013年期间出现大幅波动,尤其是从2012年开始,生态环境保护权重开始超过经济发展的权重,但整体上变化幅度不大,从期初的03196上升至期末的03255;绿色生产与资源消费和社会公平在2011年的数值差距不大,分别为01855和01827,但在接下来年份里,绿色生产与资源消费整体上呈现递增趋势,上升至2016年的01934,而社会公平整体上则呈现递减趋势,下降至2016年的01374。上述结果表明,在长江经济带经济社会建设过程中,各地方政府在提高经济发展质量的同时,愈发注重以减少资源消耗和改善生态环境为硬约束条件,将绿色发展理念融入长江经济带发展建设中。
表3报告了2011—2016年长江经济带整体和各大区域包容性绿色增长水平的测量结果的描述性统计。从整体层面看,长江经济带110个城市包容性绿色增长的均值和标准差总体上分别以2013年和2014年为拐点,呈现先下降后上升的“U型”变化趋势,造成均值在2013年骤降的主要原因可能是在2012后,我国GDP增速由过去9%以上的高速增长变为6%—7%的中高速增长,经济开始从数量型增长转变为质量型增长;此外,各年的极大值和极小值的数量差距也呈现明显减小趋势。从各大区域的均值来看,下游>中游>上游,其中,上游、中游地区的期末均值与期初均值无明显差异,但下游地区的均值较期初发生了明显的增加,从2011年的04068上升至2016年的04423;从各大区域的标准差来看,上游、中游地区总体上无明显变化,而下游地区则有显著波动,说明整体的标准差可能主要是下游地区所造成的;从各大区域的极值来看,上游、中游地区期末的最大、最小值较期初均有明显提升,特别是最大值的变化最为显著,但下游地区期末的最大、最小值较期初则出现明显下降,说明各区域间包容性绿色增长的极值差正在逐渐减小。
(二)包容性绿色增长的均等化水平测算
基于2011—2016年长江经济带110个城市包容性绿色增长的综合得分,根据式(12)、(13)和(14)分别计算长江经济带整体和区域间包容性绿色增长的基尼系数、泰尔指数和对数离差均值,结果见表4。
从表4报告的长江经济带整体差异来看,长江经济带包容性绿色增长存在着较为明显的市际差异。其中基尼系数、泰尔指数和对数离差均值均在2013年达到最大值,表明2013年长江经济带各城市之间的包容性绿色增长水平的差异最大;从各指数的整体变化趋势来看,均以2013年为拐点,呈现先上升后下降的“倒U”型变化趋势,表明长江经济带各城市的包容性绿色发展水平的整体差异在2013年后在不断缩小。为深入探究各区域间和区域内的差异水平,本文借鉴刘亦文等(2016)[17]文献的做法,将整体泰尔指数和对数离差均值进一步分解①,结果见表5和表6。①①本文的上游地区界定为云南、贵州、四川和重庆的33个城市;中游地区界定为湖北、湖南、江西和安徽的52个城市;下游地区界定为江苏、浙江和上海的25个城市;共计110个城市。
表5和表6报告了差异的分解结构。泰尔指数和对数离差均值所描述的各大区域差异特征大致相同,其中下游城市群之间的整体差异程度最小,均值分别为00902和00947;中游城市群之间的整体差异程度最大,均值分别为01339和01276;上游城市群之间各年的差异水平总体上波动幅度最小,极大极小值差为00265和00299;各大区域的上述两个指标均具有明显的阶段特征,在2011—2012年呈现逐年递增趋势,在2013年后表现为明显的回落趋势;通过比较泰尔指数和对数离差均值的区域内差异与区域间差异的数值来看,区域内差异均显著的大于区域间差异,说明长江经济带包容性绿色增长水平的主要差异是由各区域城市群内的差异所造成的;此外,区域间差异占总差异的比重整体上呈逐年递增趋势,表明各大区域之间的差异日益凸显。
(三)区域包容性绿色增长差异的收敛性分析
为探究长江经济带包容性绿色增长的区域差异是否具有收敛特征,本文分别从σ收敛模型、绝对β收敛模型和条件β收敛模型对区域差异的收敛性进行实证分析。
表7报告了2011—2016年长江经济带整体和三大区域包容性绿色增长的σ收敛系数值。从表7可看出,无论是从长江经济带整体层面,还是上、中、下游城市群,σ收敛系数以2013年为转折点,呈现出先上升后下降的趋势。其中,下游城市群的上升和下降幅度最大,中游城市群次之,上游城市群最小。这表明长江经济带整体和三大区域的包容性绿色增长存在着明显的先发散后σ收敛的特征,且下游城市群的发散和收敛速度最快,上游城市群的发散和收敛速度最慢,即在2013年前后下游城市群差异扩大和缩小的速度最快。
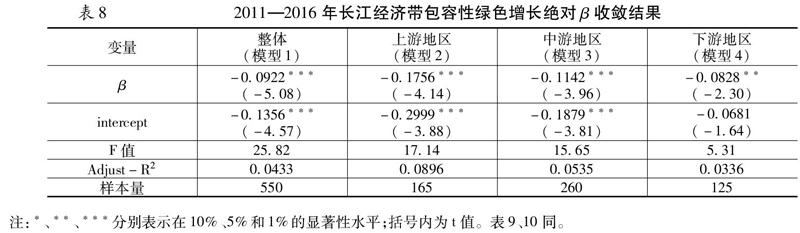
表7仅从存量视角分析了长江经济带各大区域包容性绿色增长的收敛性,为进一步各市域及各大区域在长期的变化趋势中是否具有收敛特征,需要引入β收敛模型进行检验。2011-2016年长江经济带包容性绿色增长水平的绝对β收敛结果如表8所示。从长江经济带整体层面来看,β收敛系数显著为负,表明长江经济带包容性绿色增长水平与初始水平成负相关,各城市包容性绿色增长水平具有明显的绝对β收敛特征,即存在着包容性绿色增长期初水平相对较低的城市加快赶超包容性绿色增长水平相对较高的城市。从各大区域的检验结果来看,上、中、下游城市群的β收敛系数均为负值,且至少通过5%显著性水平检验,说明各区域都具有显著的β收敛特征,各区域内部的各城市之间具有共同的稳态,市域间的包容性绿色发展水平的差异呈现不断缩小的态势。此外,通过比较各区域β收敛系数的绝对值可以看出,上、中游城市群的绝对β收敛速度明显的快于长江经济带整体平均水平和下游城市群水平,这反映出各区域具有不同的收敛速度,即在不考虑外在因素的条件下,存在着经济发展水平相对欠发达的落后者(上、中游城市群)对领先者(下游城市群)的“追赶效应”。
综合现有文献研究,本文分别引入技术创新、人力资本水平以及制度變迁等控制变量检验长江经济带包容性绿色增长的条件β收敛特征①。其中,技术创新选用各城市的政府财政支出中用于科学技术支出的部分来表示,通过取对数处理方式避免异方差等问题。通常,如果城市财政在研发资金上的投入越多,其生产技术水平提升得越快,可以加快促进传统“三高”产业向高新技术产业的演进,提高产业的增加值和地区生产总值;人力资本水平选用各城市普通高等学校在校学生数量占所在地区年末人口数量的比例来衡量,通常,城市的人力资本水平直接决定了当地产业结构的高度,对人力资本水平较低的地区往往适合发展劳动密集型产业或资本密集型等低附加值产业,而人力资本水平较高的地区往往适合发展技术密集型等高附加值产业;制度变迁选用各城市实际利用外商投资额来测量,具体测算方法为将各城市每年的实际利用外资额通过当年美元兑人民币的实际汇率进行转化,同样,通过取对数处理避免异方差问题,通常,外资的流入可以带动、盘活我国廉价、充裕的劳动力以及其他丰富的初级生产要素,此外还可以将较为先进的生产技术带入到我国,优化我国生产要素的资源配置。2011—2016年长江经济带整体和三大区域包容性绿色增长水平的条件β收敛结果如表9和表10所示。①①彭国华(2005)认为引入控制变量会造成条件β收敛检验结果出现偏差,因此本文采用逐步加入控制变量分析。实验结果显示加入技术创新、人力资本水平以及制度变迁等控制变量不会影响到各区域β收敛检验结果。
表9和表10分别报告了长江经济带整体和上、中、下游城市群包容性绿色增长水平的条件β收敛检验结果。可以看出,无论是从长江经济带整体层面,还是三大城市群层面,β收敛系数均为负值,且均通过1%显著性水平检验,表明长江经济带各区域包容性绿色增长的差异存在显著的条件β收敛特征,即整体和各区域内部的各城市之间具有共同的稳态水平,市域间的包容性绿色发展水平的差异呈现不断缩小的态势。通过比较各区域β收敛系数的绝对值可以看出,上、中游城市群的条件β收敛速度明显的快于下游城市群,具体而言,上游城市群的条件β收敛速度最快,正处于追赶包容性绿色增长水平较高的中、下游城市群的过程中,但从未来短期来看,各区域间的包容性绿色增长水平差距仍将明显存在。此外,各控制变量在整体和各大区域的实证结果不完全相同。其中,技术创新的系数无论是在整体层面,还是三大城市群层面都为正值,且均通过10%显著性水平检验,表明技术创新有助于长江经济带市域和各大区域的差异收敛。此外,下游城市群的技术创新系数值远高于上、中游城市群,说明技术创新的提升对促进下游地区包容性绿色增长的收敛作用更大;人力资本水平系数除在下游城市群显著为负以外,在整体和上、中游城市群层面都显著为正数,表明人力资本水平的提升有利于整体和上、中游地区内市域包容性绿色增长的收敛,而对下游地区内市域包容性绿色增长的收敛则表现出抑制作用;制度变迁的系数对整体和上、中游地区为正数,对下游地区为负数,但均未能通过统计显著性检验。
五、主要结论与启示
本文根据包容性绿色增长的概念和内涵,借鉴现有学者的研究成果,针对长江经济带包容性绿色增长设计出指标评价体系,选用熵权TOPSIS法测度了2011—2016年长江经济带110个城市的包容性绿色增长水平,并基于测度结果,运用基尼系数、泰尔指数、对数离差均值等差异性评价指标以及σ收敛模型、绝对β收敛模型、条件β收敛模型分别研究各大区域差异性和收敛特征。主要研究结论如下:
第一,测度结果显示:经济发展和生态环境保护在包容性绿色增长中所占比重最大。绿色生产与消费和社会公平的权重在期初基本相同,但随后,绿色生产与消费的权重值整体上呈现递增趋势,而社会公平的权重值整体上则呈现递减趋势。长江经济带110个城市包容性绿色增长的均值和标准差整体上分别以2013年和2014年为拐点,呈现先下降后上升的“U型”变化趋势。各年的极大值和极小值的数量差距也呈现明显减小趋势。各区域间包容性绿色增长水平差异显著,整体表现为“下游>中游>上游”分布。从各大区域内城市包容性绿色增长水平的前十排名来看,上、下游城市群相对比较稳定,而中游地区的动态变化较大。
第二,各差异性统计指标的测算结果表明,观察期内长江经济包容性绿色增长存在显著的区域差异,从各指数的整体变化趋势来看,均以2013年为拐点,呈现先上升后下降的“倒U”型变化趋势;通过对泰尔指数和对数离差均值进一步分解可发现,各大区域内城市差异程度表現为“中游>上游>下游”,各年的区域差异主要是由区域内差异所造成的。
第三,长江经济带各区域包容性绿色增长存在显著的收敛性。其中,长江经济带整体和各大区域在2013年后表现出明显的σ收敛特征;绝对β收敛检验结果显示,上、中游城市群β收敛系数的绝对值明显大于下游城市群β收敛系数的绝对值,存在着经济发展水平相对欠发达的落后者(上、中游城市群)对领先者(下游城市群)的“追赶效应”;条件β收敛检验结果显示,加强技术创新和提升人力资本水平对促进整体和三大区域包容性绿色增长的收敛具有积极作用,制度变迁对影响包容性绿色增长的收敛作用不显著。
基于此,本文提出以下建议:首先,加快转变长江经济带的发展理念,坚持走生态优先,绿色发展之路,转变“唯GDP论英雄”的发展思路,将包容性绿色增长纳入各级政府考核中,更加关注社会民生领域的建设和生态文明建设。其次,对于上游城市群而言,应积极寻找新的经济增长点,比如依托现代旅游业和现代服务业,促进产业结构转型升级,同时兼顾公平与效率的收入分配制度,重点提高城乡居民收入,加快户籍制度改革,积极探索在人才流动、资本投资、技术研发等方面的引导机制,促进资源要素在城乡之间、地区之间的合理配置。再者,对于中游城市群而言,应积极探索基本公共服务的供给模式创新,有效增加和提高基本公共服务供给的数量与质量,特别是针对老少边贫等落后地区,更应该发挥政府基本公共服务的兜底作用,加大力度补齐民生领域的短板,消除贫困代际转移的发生。最后,对于下游城市群而言,应努力摸索在财政、金融、投资、市场化等领域的政策工具创新,鼓励、扶持有条件的企业绿色循环生产,倡导居民绿色消费的方式,树立以资源环境为红线的发展意识;在生态环境保护方面,加快构建政府生态环境保护的绩效考核、保护督察和责任问责机制,完善长江经济带各省、市际政府间的横向生态补偿机制。
参考文献:
[1]Org Z. Inclusive Green Growth: The Pathway to Sustainable Development[M]. World Bank, 2012.
[2]OECD. Inclusive Green Growth: For the Future We Want[R]. OECD Working Paper, 2012.
[3]张晓颖. 经济、环境、社会发展与人:从可持续发展观到包容性绿色增长[J]. 江淮论坛,2014(06):93-98.
[4]张芮嘉. 浅谈川甘青结合部藏区生态补偿及绿色包容性增长[J]. 现代经济信息,2015(23):465+484.
[5]杨雪星. 包容性绿色经济增长指数构建与实证研究——基于G20国家数据[J]. 福建论坛(人文社会科学版),2014(06):42-48.
[6]徐宝亮,钟海燕. 中国经济增长的绿色包容性:基于FA的动态测度[J]. 科技管理研究,2015,35(12):214-219.
[7]吴武林,周小亮. 中国包容性绿色增长测算评价与影响因素研究[J]. 社会科学研究,2018(01):27-37.
[8]胡书芳,马宪法. 浙江省城市绿色发展水平评价及区域差异分析[J]. 科技管理研究,2017,37(07):110-114.
[9]赵吉.城市支点、协调发展与长江经济带城市群走向[J].重庆社会科学, 2017(2):42-49.
[10]张泽义.环境污染、长江经济带绿色城镇化效率及其影响因素——基于综合城镇化视角[J].财经论丛,2018(2):3-10.
[11]周正柱.长江经济带城镇化质量时空格局演变及未来趋势[J].深圳大学学报(人文社会科学版),2018(4):62-71.
[12]余兴厚,熊兴. 居民资源禀赋、主体认知与基本公共服务满意度——基于三峡库区829份调查问卷的实证分析[J]. 西部论坛,2018,28(05):99-108.
[13]Olson D L . Comparison of weights in TOPSIS models[M]. Elsevier Science Publishers B. V. 2004.
[14]刘明,王思文. β收敛、空间依赖与中国制造业发展[J]. 数量经济技术经济研究,2018,35(02):3-23.
[15]王许亮,王恕立. 服务业能源生产率变迁及收敛性分析——基于全球40个经济体细分行业数据的经验研究[J]. 数量经济技术经济研究,2018,35(01):42-59.
[16]滕泽伟,胡宗彪,蒋西艳. 中国服务业碳生产率变动的差异及收敛性研究[J]. 数量经济技术经济研究,2017,34(03):78-94.
[17]刘亦文,文晓茜,胡宗义. 中国污染物排放的地区差异及收敛性研究[J]. 数量经济技术经济研究,2016,33(04):78-94.
责任编辑:张士斌
