基于PCA与核PCA的微阵列数据分析

黄紫成，林增坦

(仰恩大学工程技术学院，福建泉州 362014)

微阵列技术是近年来生物信息领域出现的新兴技术，已被广泛应用于药物研究、疾病诊断、基因测试等多个领域[1]。微阵列技术所呈现的数据以矩阵形式表示，也称为基因表达数据，当前对微阵列的数据分析主要有差异表达分析、聚类分析、样本分类、调控网络、荟萃分析等。本文根据研究需要，重点进行样本分类分析，该分析是为了建立有效的疾病诊断，使用机器学习算法对微阵列数据进行学习，得出预测模型，进而再对未知分类的表达数据进行分类判别，为疾病的诊断及治疗提供可靠的分类效果。由于微阵列数据存在着维数多而样本少的问题，如何有效地对基因数据进行分析，选出具有特殊贡献的特征基因，提高分类效率，是当前基因数据样本分类分析的研究热点之一[2]。

目前，有越来越多的特征选择算法应用于微阵列数据的降维分析，并能得到好的分类效果，典型的算法有主成分分析(PCA)[3]、非负矩阵分解、独立分量分析等，常用的分类算法有支持向量机(SVM)、贝叶斯分类等，把微阵列数据降维之后再采用支持向量机等分类器计算识别率，能得到较高准确率。本文使用PCA与核PCA对微阵列数据进行降维处理，再计算经过这两种算法处理过的识别率，对比分析运用两种算法处理微阵列数据效果的优劣。

1 算法理论介绍

1.1 主成分分析(PCA)

主成分分析是一种统计学方法，也是数据挖掘中常用的一种降维算法，它能在损失很少信息的前提下，把多个指标转化为几个综合指标，通常把转化生成的综合指标称之为主成分。

算法有如下几个步骤[4]：

(3)求系数矩阵R的特征根与特征向量λ1≥λ2≥…≥λp>0，相应正交特征向量为ai=[a1i,a2i,…,api]T,i=1,2,…,p.

(5)确定主成分个数，目标是用较少的主成分提取更多的原始信息，取决于k和α(k)之间的权衡。一方面，应该使k尽可能小；另一方面，使累积贡献率α(k)尽可能大。在实际使用中，通常取αk≥85%[4]。

1.2 核主成分分析(KPCA)

核主成分分析是目前比较流行的一种新的特征提取方法，它是对PCA的非线性推广，核函数的形式为k(xi,xj)=<φ(xi),φ(xj)>，其中，k函数为核函数，<,>为内积。算法简要步骤如下[5]。

(1)计算矩阵k(xi,xj)；

(2)计算矩阵k(xi,xj)的m个特征值和特征向量；

(3)对m个特征向量进行归一化处理；

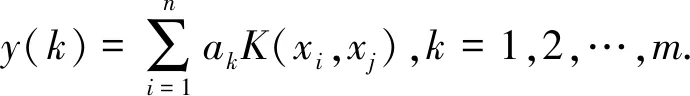
1.3 支持向量机(SVM)

支持向量机(SVM)是以统计学理论为基础，根据结构风险最小化原则提出来的。支持向量机的分类实际是通过非线性的变换将输入空间变换到一个高维的空间，接着在此新空间求最优线性分类面，通过定义适当内积函数来实现这种非线性变换[6]。支持向量机主要有三种内积函数。

(1)多项式形式的内积函数K(x,xi)=[(x·xi)+1]q，经计算得到的是一个以q阶多项式为分离器的支持向量机。

(3)S形函数内积K(x,xi)=tanh(v(x·xi)+c)。

2 实验结果与分析

本实验使用经典的基因数据集Leukemia[7-8]，该数据集包含了7129个基因，其中，训练集有38个样本(27个ALL，11个AML)，测试集有34个样本(20个ALL，14个AML)。

2.1 数据预处理

在基因变量中，由于受条件限制，存在很多噪声基因，这些基因会对分类结果产生干扰，在进行特征选择之前，需要先预处理，即基因筛选。本文选用的基因筛选方法是基因排序方法。计算各个基因的t值[9-11]，具体公式如下：

2.2 实验结果

实验环境为Win7 64bit 操作系统，8GB内存，Intel®Core i7，Matlab R2017a，SVM工具箱使用台湾林智仁教授开发的Libsvm[12]。支持向量机以径向基BRF作为核函数，利用数据集中训练集进行训练，选取出一个最优交叉验证准确率，得到σ与惩罚参数C，构造分类器模型。利用此模型对测试集进行测试，计算识别率。在实验中利用PCA与核PCA将数据降维到低维，在进行SVM分类识别，两种特征选择算法识别率如表1所示。经过PCA降维之后，最优识别率可以达到97.0588%，34个样本中有33个被正确识别。

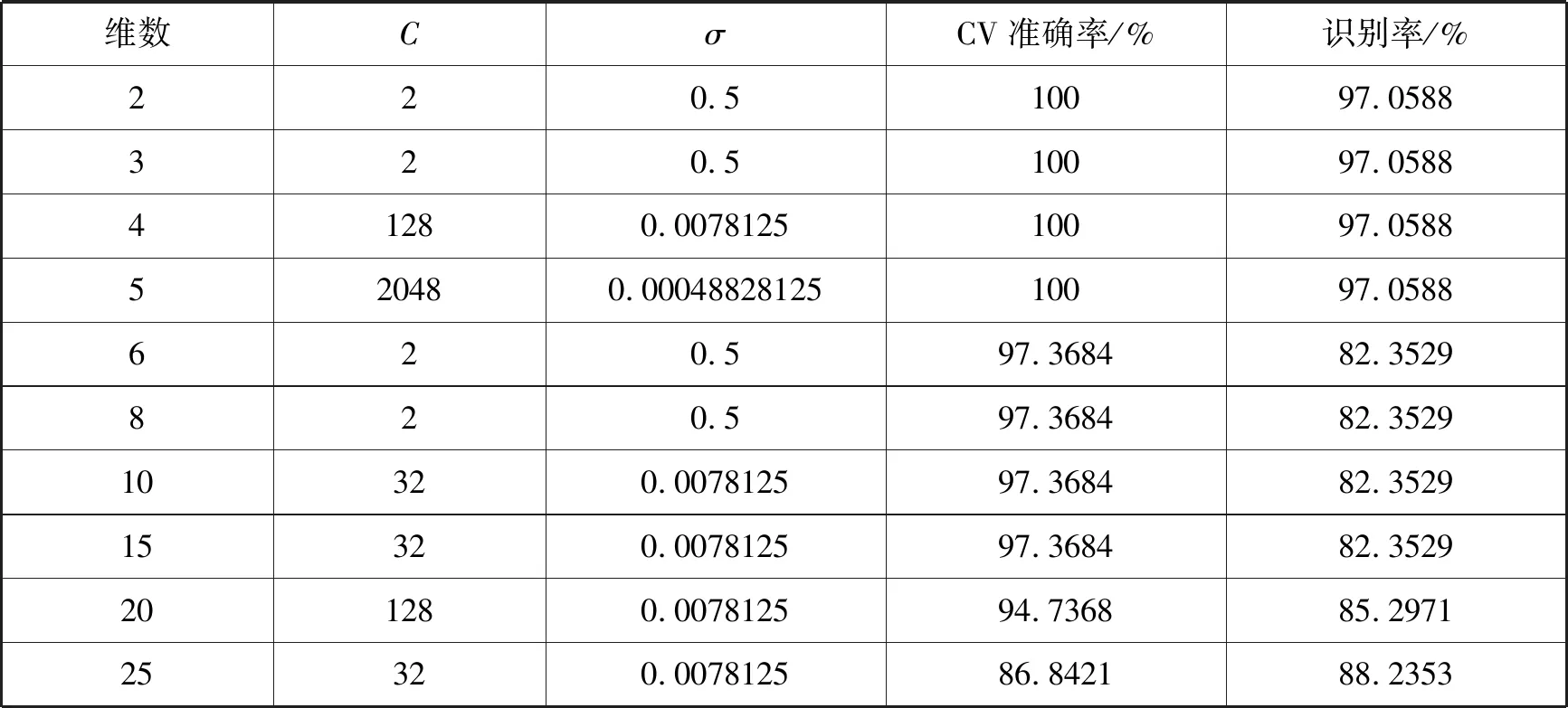
表1 PCA特征提取后识别率

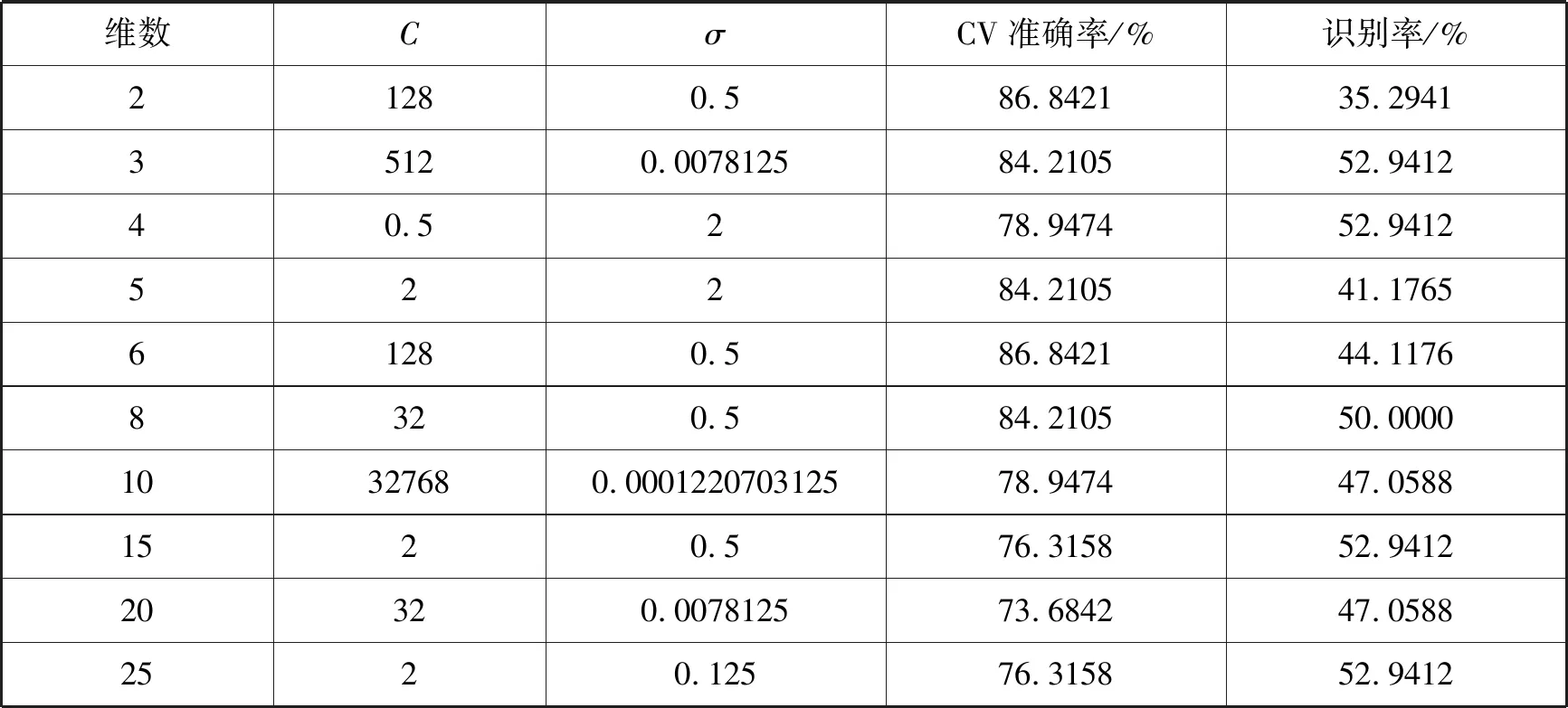
表2 核PCA特征提取后识别率

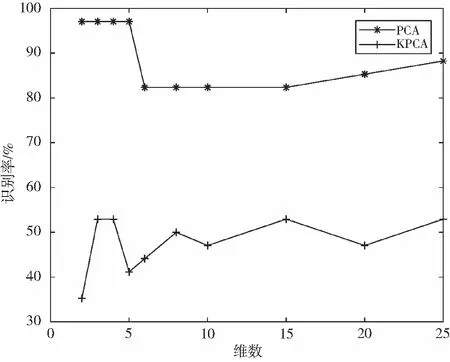
图1 PCA与KPCA在不同维数识别率比较

从表2可以看出，核PCA降维之后，效果不是很好，最优的识别率只有52.9412%，34个测试样本只有18个被正确识别。为了更直观地对比两种算法特征提取之后的识别率，画出图形如图1所示。经过PCA特征提取之后的识别率高于KPCA，这说明PCA作为经典降维算法应用的广泛性，对微阵列数据来说亦是如此。微阵列数据经过降维分析之后，提高了分类识别率，有利于医学上对一些疾病的识别。

3 结语

综上所述，根据微阵列数据的特征，计算t值进行筛选预处理，使用PCA与核PCA对数据进行特征提取，利用基于径向基BRF作为核函数的支持向量机进行分类，计算分类识别率。实验结果表明，基于PCA降维处理之后其最优识别率达到97.0588%，34个测试样本有33个被正确识别，而核PCA效果不理想，最优识别率只达到52.9412%。因此，针对微阵列数据高维小样本的特点，采用降维处理方法进行分析可以提高分类的准确性。