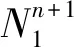Lorentz空间中具有平行Ricci曲率的2-调和类空超曲面研究
2019-06-20杨云飞
杨云飞
(内蒙古师范大学,内蒙古呼和浩特 010022)
1 研究背景
现代微分流形理论的微分几何在近代数学和物理学中具有重要作用,成为近代物理学、数学及力学不可缺少的数学工具.微分流形在现实生活中的运用十分广泛,包括在地震波传播中计算波传播振幅的焦散问题,飞机控制系统的应用,在人造卫星控制系统的应用,也包括物理、气象等方面的运用.根据J Eells的思想,姜国英研究了黎曼流形空间2-调和的等距浸入.近代由于对高维空间的微分几何和曲线、曲面整体性质的研究,使微分几何学与黎曼几何、拓扑学、变分学、李群代数等有了密切关系,互相渗透,成为现代数学的中心问题之一.刘育江[1]推出了在黎曼空间中具有Ricci曲率平行空间中的2-调和超曲面,并给出这类超曲面关于其第二基本形式模长平方S的积分不等式及刚性定理;2000年,欧阳崇珍[2]研究了伪黎曼空间型的2-调和类空子流形,得到了常曲率的伪黎曼流形的类空子流形为2-调和的充要条件.
2 文献综述
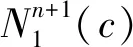
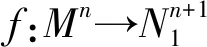
定理设Mn是Lorentz中具有平行Ricci曲率的2-调和紧致无边类空超曲面,H为Mn的平均曲率,S为其第二基本形式的模长的平方,0 本文约定指标范围:1≤A,B,C,…≤n+1,1≤i,j,k,…≤n. (1) (2) KABCD=cεAεB(δACδBD-δADδBC). (3) 限制在M上,则有: (4) (5) (6) Rijkl=c(δikδjl-δjlδjk)-(hikhjl-hilhjk)=Kijkl-(hikhjl-hilhjk). (7) (8) 由式(6)有: (9) 则有: hijk=hikj+Kn+1ijk. (10) (11) (12) 以KABCD,E表示KABCD的共变微分,Kn+1ijkl=Kn+1ijkl+Kn+1in+1khjl+Kn+1ijn+1hkl+Kmijkhml. (13) (14) 由Mn的2-调和超曲面,由文献[2]的定理1可知: (15) 由于Ricci曲率平行,则: (16) (17) (18) 等式成立当且仅当至少n-1个ui=λi-H,则: (19) 下面计算第二基本形式模长平方的Laplacian,由式(17)可得: (20) 由式(10)和(16)可得: (21) 由于Mn是2-调和类空超曲面,可由Riemann流形间2-调和等距浸入得: (22) 选取Mn的主方向为标准正交架场,使得: hij=λiδij. (23) (24) (25) 令f2=S-nH2, (26) (27) 所以由式(7)(24)(26)得到: (28) 通过梯度算子可得: (29) (30) 由于Mn是紧致无边可定向的超曲面,两边积分,利用Green散度定理,得积分不等式: (31) 即定理得证. 由式(2)(31)可以知道等号成立,从而式(20)(28)(29)等号成立.可以设1-δ=b-a=0,从而Nn+1是具有截面曲率为1的常曲率空间Sn+1(1). 综上可以得到: (32) 另外(28)等号成立,可知λ1,λ2,…,λn中至多有两个不同. 当λ1=λ2=…=λn时,则λ1=λ2=…=λn=λ,故Mn是常曲率Sn+1(1)全脐类空超曲面. 当λ1=λ2=…=λn-1=λ,λn=μ时,其中λ,μ为函数,即Mn是Sn+1(1)中具有两个不同主曲率的全脐类空超曲面的标准乘积.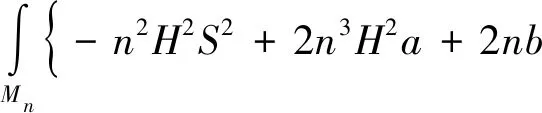
3 理论知识
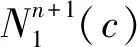
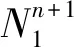

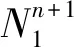
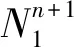
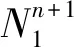
4 相关定理及证明
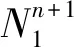


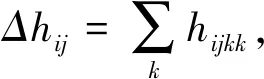
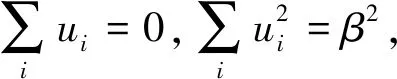
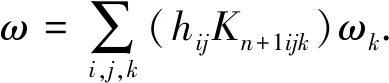


5 结论