考虑区域平衡的最优负荷控制两阶段算法

2019-06-20姚国强姚剑峰刘文峰焦振军魏杰邵永青

广东电力 2019年6期

关键词：平衡性负荷量整数

姚国强, 姚剑峰, 刘文峰，焦振军，魏杰，邵永青

(国网浙江省电力有限公司嘉兴供电公司，浙江嘉兴 314000)

最优负荷控制是电网在突发状况下可靠运行的核心技术之一。当系统发生严重故障(如特高压输电线路故障)或突然失去大量电源后，快速切除部分负荷可以解决线路潮流超限额、发供电不平衡、电网频率下降等问题，从而保证系统稳定运行[1]。

实际电网调度工作中需要考虑的最优负荷控制手段主要有以下特点：

a)实时性。要求负荷控制在一定时间内完成，实际中一般为分钟级。

b)离散性。切负荷量不是连续可控的，一条线路只有切除或不切除两种情况，即整数规划问题。

c)选择性。鉴于实际电力用户的重要性差别很大，负荷控制有预先制定的拉限电名单，切除线路一般在拉限电名单中选取。

d)区域平衡性。当一个地区发供电极度不平衡或受限于某一供电瓶颈时，需要对整个地区实施负荷控制措施，此时地区中各县域一般按分配指标进行负荷控制，从而达到地区内部负荷分布的相对均衡。

由于最优负荷控制是电网在突发状况下可靠运行的重要基础，学术界和电力企业对于其模型和算法进行了大量研究。在最优负荷控制模型方面，文献[2]提出一种基于空间静态电压稳定域的最优负荷控制模型，文献[3]提出一种考虑故障电压恢复的最优负荷控制模型，文献[4]提出一种基于静态电压稳定裕度的最优负荷控制模型，文献[5]提出一种考虑暂态稳定微分代数方程组约束的最优负荷控制模型，文献[6]提出一种计及主变压器上层油温约束的最优负荷控制模型。以上研究主要集中于考虑暂态稳定和电压稳定，所采用的模型能及时稳定暂态波动或电压波动对电网的冲击，但对考虑区域平衡的最优负荷控制模型鲜有讨论，同时在模型求解的快速性上也存在一定缺陷。文献[7]提出了一种协调经济性及事故评级的最优负荷控制模型，可相对均衡事故评级；文献[8]提出一种考虑温控负荷的最优负荷控制模型，消除了温控负荷群体聚合功率的大幅波动；文献[9]提出一种基于风险量化管理方法的最优过载切负荷模型，兼顾了电网安全性和经济性的要求；文献[10]提出一种考虑负荷控制顺序、重要等级、分区及裕度的多目标批量最优负荷控制模型，并研制了一套批量负荷快速控制系统，实用化程度较高；文献[11]提出一种基于二阶锥规划的最优负荷控制模型，所提的凸模型可稳定高效地进行求解；文献[12]提出一种计及发电机出力及负荷不确定性的模糊最优切负荷模型，验证了计及不确定性的必要性；文献[13]提出一种基于灵敏度分析和潮流熵的最优切负荷模型，通过模糊多属性决策法，兼顾局部过负荷和全局线路过负荷的问题。以上研究也没有考虑多区域最优负荷控制中各个区域负荷控制的平衡性。

在最优负荷控制优化算法方面，文献[14]提出一种基于改进粒子群算法的交直流系统低压最优负荷控制策略，文献[15]提出一种基于遗传算法和神经网络的最优负荷控制混合算法，文献[16]提出一种基于改进遗传算法的交直流系统最优切负荷算法，文献[17]提出一种基于综合贡献度指标的最优切负荷多目标优化方法，但采用智能优化算法难以保证算法求解的快速性和最优性。文献[18]提出一种基于数据驱动的最优负荷控制优化算法，结果具有较高的精度，但算法求解的速度较慢；文献[19]提出一种最优负荷控制问题的并行模式搜索算法，提高了算法的求解速度，但算法难以实现模型的稳定和最优求解；文献[20]提出一种恢复潮流可行解的最优负荷控制模型，通过二次约束二次优化问题的描述将海森矩阵表述成定常矩阵，大大缩短了预测-校正原对偶内点法的求解时间；文献[21]提出一种基于灵敏度分析的最优负荷控制优化算法，采用原对偶内点法求解最优负荷控制模型，提高了负荷控制模型的计算效率。

在最优负荷控制功能应用方面，文献[22]研究了基于D5000平台的负荷控制技术，提出了负荷批量顺序控制功能实现过程中的关键问题和处理措施；文献[23]研究了基于IEC104规约的负荷控制技术，实现了省地负荷批量控制功能。

本文提出一种考虑区域平衡的最优负荷控制两阶段优化算法，该算法分2个阶段：第1阶段，构建最优负荷控制的混合整数线性规划模型，对相互独立的单区域最优负荷控制问题进行并行计算，得到每个区域的足量切负荷量和缺量切负荷量，模型的高效分解和算法的并行计算保证了算法求解的实时性；第2阶段，利用第一阶段的结果初始化所有区域负荷控制平衡优化的混合整数线性规划模型，对多区域最优负荷控制进行统筹优化，保证每个地区内部负荷分布的相对均衡。

1 考虑区域平衡的最优负荷控制模型

1.1 目标函数

最优负荷控制问题主要研究通过切除电网的负荷，消除线路潮流超限额、发供电不平衡、电网频率下降等问题。当一个地区发供电极度不平衡或受限于某一供电瓶颈时，需要对整个地区实施负荷控制措施，此时地区中的各县域一般按分配指标进行负荷控制，每个区域切除一部分负荷，从而达到地区内部负荷分布的相对均衡。因此，需要研究考虑区域平衡的最优负荷控制问题，选取关键切负荷点，制定各负荷点的切负荷量策略。

考虑区域平衡的最优负荷控制模型，其目标函数取各区域总加权的切除负荷最小，即

(1)

1.2 约束条件

最优负荷控制问题需要考虑切负荷总量约束和区域平衡性约束。

1.2.1 切负荷总量约束

整个地区的切负荷总量应大于切负荷目标值T，以保证切负荷措施后系统保持稳定、联络线不超限额及系统发供电平衡等，即

(2)

1.2.2 区域平衡性约束

(3)

(4)

利用方差描述各个区域切除比例的偏差如式(5)所示：

(5)

(6)

本文所提算法采用如式(4)所示的偏差值约束，通过将问题划分为足量切负荷问题和缺量切负荷问题，使式(4)中含绝对值的约束线性化。

2 考虑区域平衡的最优负荷控制算法

2.1 算法结构

当各区域分别按分配指标进行负荷控制时，具体思路如图1(a)所示，每个区域切除负荷将大于其分配指标，从而使总切除负荷比目标值T更大。本文提出的考虑区域平衡最优切负荷算法采用“盈亏互补”的思想，统筹考虑各区域的切负荷量，寻求总切除负荷最小的策略，具体思路如图1(b)所示。在某些区域切除负荷略大于其分配指标而其他某些区域切除负荷略小于其分配指标，且足量负荷(指标线以上的阴影部分)大于缺量负荷(指标线以下的阴影部分)的特定情况下，通过两阶段最优负荷控制，使总切除负荷大于目标值T而小于图1(a)得到的总切除负荷，且使每个区域切除的负荷在分配指标附近。

图1 多区域切负荷思路比较Fig.1 Contrast of ideas of multi-area load shedding

式(1)—(4)的负荷控制模型是一个混合整数非线性规划问题。其中，在区域平衡约束式(4)中采用各区域偏差总和小于ε的方式，ε是一个极小量。实际中ε不能取任意小的值，若ε取值太小，因为不一定存在绝对平衡的解，式(4)会使负荷控制问题无解，而ε取太大又使得解趋向于切除量最小而平衡性不够。因此，常规的智能算法求解式(1)—(4)的负荷控制模型不稳定，对于不同的ε取值，求解结果差别较大。实际中负荷控制基于不确定性的负荷进行，需要稳定且较优的解作为保证。考虑到式(4)中含绝对值的非线性约束，通过将最优负荷控制问题划分为足量切负荷问题和缺量切负荷问题来使式(4)中含绝对值的约束线性化，将考虑区域平衡的最优负荷控制模型转变为第一阶段单区域计算的混合整数线性规划模型。因此，所提算法是上述模型的严格求解方法。

算法将求解过程分为单区域计算和统筹优化两个阶段。在单区域计算阶段，每个区域独立计算各自的足量切负荷问题和缺量切负荷问题，共计算2m个含少量0-1整数变量的混合整数线性规划问题，且可以并行计算。在统筹优化阶段，利用单区域计算结果，进行区域平衡优化问题的求解，得到最终的最优负荷控制策略。算法流程主框架如图2所示。

图2 算法流程主框架Fig.2 Main framework of algorithm process

2.2 单区域足量(缺量)切负荷问题

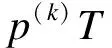
(7)

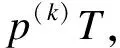
(8)

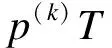
(9)

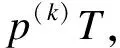
(10)

将缺量切负荷问题转化成标准的最小化问题，即

(11)

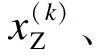
(12)

(13)

2.3 区域平衡优化问题

区域平衡优化问题的目标函数为

(14)

约束条件为

(15)

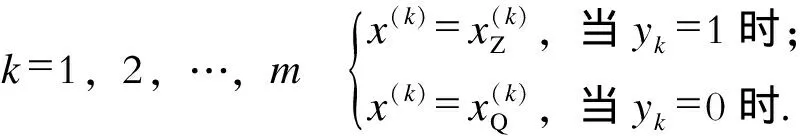
(16)

通过以上变换，区域平衡优化问题成功表述为一个混合整数线性规划问题。通过算法分解，将求解过程分为单区域计算和统筹优化两个阶段，而单区域计算阶段的足量(缺量)切负荷问题和统筹优化阶段的区域平衡优化问题都表述为标准的混合整数线性规划问题，从而可以灵活选取统一的求解方法，保证了算法本身结构和求解方法的独立性，利于合理搭配，实现了求解算法和模型的相互独立。

3 算例分析

3.1 对比算法

为了验证算法的效果，将实际中常用的地区负荷控制方法与本文算法进行比较，以下算法模型均为混合整数线性规划问题，采用基于分支定界算法的混合整数线性规划求解器CPLEX。基于各个算法，在MATLAB R2016a上进行编程，利用YALMIP工具包及CPLEX解算器进行建模及求解，硬件环境为IntelCore(TM)i5-3340SCPU @2.8 GHz处理器，8 GB内存。

算法1：地区中各区域按分配指标独立进行负荷控制。按地区中各区域的负荷比例预先分配各区域的负荷控制指标，各区域按指标独立进行负荷控制，要求所切除负荷均比分配指标大，实际上是分别计算各区域的足量切负荷问题。

算法2：由地区中心机构统一进行负荷控制。将各区域按预定比例上报的可切负荷整合成一个可切负荷表，地区按负荷控制目标和一定的优化算法计算得到切负荷策略，进而完成负荷控制，实际上是直接计算不含区域平衡性约束的最优负荷控制问题。

算法3：本文考虑区域平衡的最优负荷控制算法。

3.2 效果比较

本文算例采用某地区实际负荷控制的相关数据，具体参数见表1。该地区共有6个区域(按县域和城区划分)，可切负荷均为10 kV和35 kV线路。

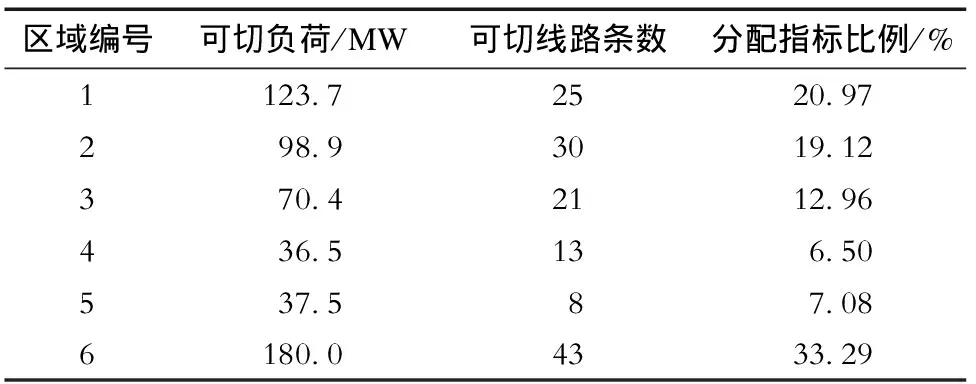
表1 算例参数Tab.1 Example parameters

选取不同的切负荷目标值T，用上述3种算法分别对本算例进行计算，得到相应的切负荷策略。表2比较了不同算法、不同目标值情况下得到的实际切负荷量，表3比较了各区域实际切负荷量与分配指标之间的最大偏差、标准差。

从结果可以看出：算法1要求各区域在不小于其分配指标的情况下独立完成负荷控制，因此偏重于区域平衡性，经济性次之；算法2在地区层面统一完成了负荷控制，力求切负荷量的经济性，而不考虑区域平衡性。算法1与算法2的特点在表2、表3中体现得很明显，即算法1较好地实现了区域平衡性(最大偏差和标准差一般在2%以内)，算法2较好地实现了经济性(平均多切负荷0.71 MW)。同时，算法1多切负荷达到了5 MW以上，算法2最大偏差和标准差平均达到了2.80%及4.04%。

表2 实际切负荷量对比Tab.2 Contrast of actual load shedding MW

注：平均多切负荷是将不同目标值T对应的多切负荷取平均值。

表3 各区域最大偏差与标准差Tab.3 Maximum deviation and standard deviation in each region %

注：括号内为标准差。

与算法1、算法2相比，本文算法(算法3)得到的切负荷策略在切负荷量和区域平衡方面都具有优势，其平均多切负荷约0.3 MW，平均最大偏差和标准差为1.53%和1.84%。具体到某一个目标值，本文算法在切负荷量方面与算法2持平或略优、比算法1可少切约5 MW负荷，在区域平衡方面与算法1持平或略优、比算法2偏差要小得多，因此本文算法同时实现了负荷控制的经济性和区域平衡性。