考虑抑制DFIG负序电流策略的配电网故障定位

2019-06-20翟学曲名新齐清

广东电力 2019年6期

翟学，曲名新，齐清

(1.湖北省电力勘测设计院有限公司，湖北武汉 430040；2.国网北京市电力公司，北京 100031)

清洁能源是当前以及未来的发展趋势，而风电在清洁能源中占有重要的地位。随着风电的发展，风电在产生清洁电能的同时也给电网带来了一定的影响。在“十三五”之前，风电场大多以单体大容量接入电网，其接入电压通常为110 kV或220 kV。近年来,由于国家政策和风电行业发展方向的调整，越来越多的小型风电，如分散式风电接入配电网[1-2]，使单电源辐射型配电网变为多电源网络[3]，增加了配电网的复杂性。双馈异步风力发电机(doubly fed induction generator，DFIG)的运行需要变流器，而变流器的控制方式对DFIG的短路电流特性有着直接的影响[4-6]，因此含风电场的配电网故障计算及其定位方案变得较为复杂。

对于DFIG短路电流特性的研究文献较多，部分研究考虑故障时的变流器闭锁，从而将DFIG等效为异步电动机，借助异步电动机的计算模型进行分析，并得出了发生三相短路时DFIG的短路电流计算公式[7]。但是目前风电场均要求具备一定的低电压穿越能力，在电网故障时还需要风电场提供一定的无功功率来支撑电网电压，因此变流器可能不再闭锁。文献[8]研究了在电网故障不严重且变流器未闭锁时DFIG的短路电流计算方法，文献[9]在研究中将DFIG等效为电势源和阻抗的串联等值电路，但是上述都是假设故障前后转子电流保持不变，且没有考虑DFIG的低电压穿越控制策略，导致计算值和仿真值存在较大误差；另一方面，当电网发生不对称故障时，会导致DFIG产生不均衡发热，转矩产生脉动[10]。为了解决该问题，文献[11]提出了消除交流侧的负序电流的策略，这样使得DFIG的短路电流特性更加复杂。

目前，国内外对于含分布式电源的配电网故障定位研究已取得一些成果。文献[12-15]对已有的算法进行了一定的改进，使得改进的配电网故障定位算法能够适应分布式电源的接入，但是以上研究都是以同步发电机为分布式电源模型，且没有考虑分布式电源的控制策略带来的影响。文献[16]在研究中考虑了光伏电站的短路电流特性，没有对其他类型分布式电源进行分析，且其定位精度不高。

为了DFIG的稳定并网，其控制策略更加完善，抑制负序电流的控制策略成为其中不可缺少的关键控制技术[11]，而对考虑该控制策略计算DFIG的短路电流的研究较少。同时，根据电力系统故障的分析与计算原理，电网中节点的故障电压是关于短路电流的数学函数，在含风电的配电网故障定位的现有研究中未充分考虑其影响。

本文在考虑抑制DFIG负序电流策略的基础上，对DFIG的短路电流特性进行分析。假定配电网中某节点故障，对含风电接入的配电网进行故障计算分析，通过比较节点的电压计算值和监测值，搜索使得相关节点误差值最小的假定故障节点，再将故障定位于一定范围内。

1 考虑抑制负序电流策略的DFIG短路电流特性分析

如图1所示，DFIG的定子绕组和转子绕组分别与电网相连，电网通过变流器向DFIG提供励磁电流，实现风电机组的变速恒频运行。

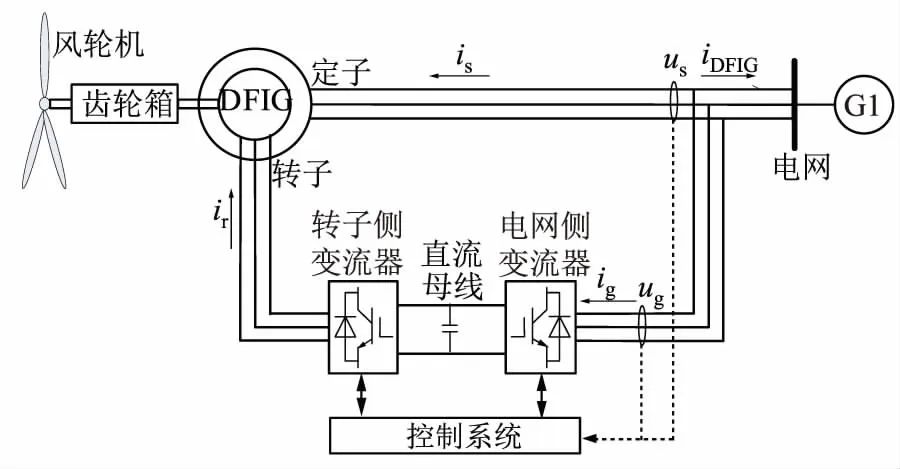
ir—转子电流；is、ig—分别为风电机组定子和电网侧变流器提供的短路电流；us、ug—分别为定子侧电压和电网侧变流器电压；uDFIG—机端电压。

图1 DFIG的结构
Fig.1 DFIG structure

当变流器正常运行时，由其结构可知DFIG输出的短路电流

if=-is-ig.

(1)

1.1 抑制定子负序电流控制

当电网发生不对称故障时，DFIG定子中会产生负序电流，导致DFIG定子的三相绕组发热不均，进而转矩可能发生脉动。为了应对上述影响，转子侧变流器采用抑制定子负序电流的控制措施，即令

(2)

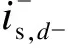
根据现有风电并网规范[17]的要求，风电场在电网故障期间要求具备一定的低电压穿越控制能力，向电网提供无功功率以支撑电网电压，具体方法是调整转子励磁电流。风电机组注入电网的无功电流

IC≥1.5(0.9-UC)IN, (0.2≤UC≤0.9).

(3)

式中：UC为风电场并网点电压标幺值；IN为风电机组的额定电流。

根据低电压穿越控制策略，得到正转坐标系下转子电流q轴分量参考值

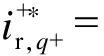
(4)

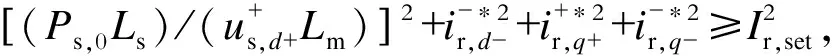
(5)

因此，可以得到DFIG定子电流的等值模型如式(6)所示，即

(6)

1.2 抑制网侧变流器负序电流

网侧变流器也采用抑制负序电流的控制策略，即

(7)

电网不对称故障条件下，电网侧交流电流的等值模型为

(8)

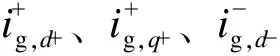
(9)

式(9)为不对称短路故障的计算公式，同样适用于三相对称故障的计算。

因此，在含DFIG的配电网短路电流计算中，要根据低电压穿越控制策略以及抑制负序电流控制策略来进行处理，为下文的含DFIG配电网故障定位奠定基础。

2 基于DFIG短路电流计算的故障定位

本文对含DFIG的配电网故障定位进行分析。当配电网中发生短路故障，可以假定是配电网中的任一节点发生故障，计算出相关节点的电压相量，与系统监测到的电压相量进行比较；通过多次假定计算能够得到某一假定点的计算结果与系统监测到的电压量最为吻合，即认为该点是离故障点最近的节点，通过同样的方法可以进一步得到故障点的准确定位。

在实际的配电网故障计算中，假定故障节点后，还需要知道故障的类型。有两种做法，第一是假定所有的故障类型，即找出使得各节点电压计算值与监测值误差最小的故障类型即为真实故障类型，该方法计算时间过长。因此，可以采用第二种方案，即先根据故障特征分析出故障的类型，本文采取基于小波神经网络故障识别方法来判断故障类型[19]，然后再通过假定计算的方法来定位故障点。

根据上述定位策略，将装有质量监测仪的节点处的监测电压与计算电压差的平方和作为误差计算函数。

(10)

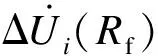
然后将所有节点都作为假定的故障点，对每一节点都进行故障计算得到一个误差函数ΔU，最后得到故障定位函数

min(ΔUi)=min(min(ΔU(Rf))i),
i=1,2,…,m.

(11)

式中：i为当前假定的节点；m为节点总数。

经过上述计算，可以得到故障的类型、离故障点最近的节点以及故障的过渡电阻，此时根据2个节点间的距离以及定位的精度要求，可将地点锁定在更小的范围内。

若已经将故障地点定位于相距L的两节点之间，要求进一步将故障地点定位在长度为l内，此时搜索故障地点的方法同上文中搜索最邻近节点相同，只是此时的节点数为(L/l)+1，相邻节点之间的距离为l。

3 仿真验证

为了验证上文所述含DFIG的配电网故障定位方法的正确性，在软件平台EMTDC中建立了IEEE 34节点系统，并对该系统进行适当变化。如图2所示，在节点814上接入DFIG机组，机组容量为1.5 MW，出口额定电压为0.69 kV，定子电阻标幺值Rs=0.01，转子电阻标幺值Rr=0.01 ，定子电感标幺值Lls=0.1 ，转子电感标幺值Llr=0.1，定转子互感标幺值Lm=3.5。DFIG采用抑制DFIG负序电流策略。

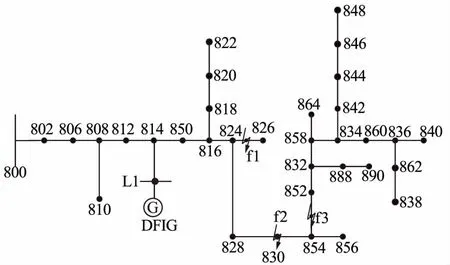
图2 算例配电网结构Fig.2 Structure of distribution network of test example

图2中的节点808、816、834、836和854装设电能质量检测仪，用以监测相应节点的电压信息。在具体的验证过程中，将仿真与本文方法以及文献[5](不考虑低电压穿越和抑制负序电流策略)中的方法结果进行对比。

3.1 短路电流计算验证

分别在图2的节点824和826线路中点f1处设置三相短路故障、在节点830(f2)处设置单相接地故障。在软件平台EMTDC仿真模型可以得到节点816处的短路电流，同时分别结合本文DFIG短路电流计算方法和文献[5]的方法在MATLAB中进行编程计算816处的短路电流，结果见表1。

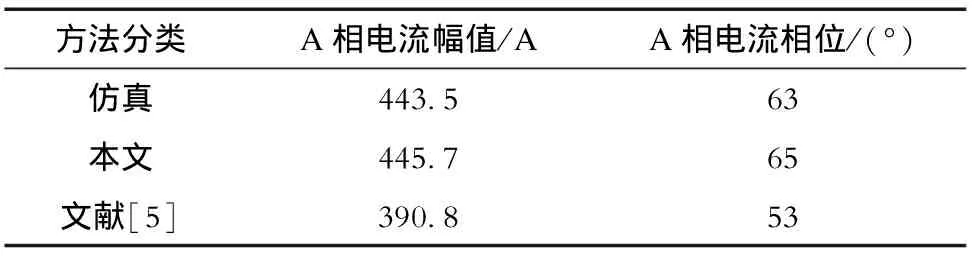
表1 f1故障时的短路电流比较结果Tab.1 Comparative results of short circuit current in fault f1

表2 f2故障时的短路电流比较结果Tab.2 Comparative results of short circuit current in fault f2

从表1和表2可以看出，通过仿真得到的节点816处的电流和本文方法计算电流幅值和相位十分接近，而文献方法与前两者方法结果相差很大。说明在考虑含DFIG的配电网故障特性时，必须考虑DFIG的控制策略，同时也说明了本文短路电流计算方法的可行性。

3.2 接入DFIG的配电网故障定位分析

分别对2种故障情况进行仿真与计算, 在EMTDC中进行如下设置：

方案A，在节点830处f2设置三相短路故障，Rf=2，要求将故障定位于2个节点之间。

方案B，在节点852和节点854之间，距离854节点4.5 km的f3点设置BC两相短路故障，Rf=5，要求将故障定位于1 km以内。利用本文方法分别搜索离故障点最邻近的节点，在MATLAB中进行编程，得到表3的结果。

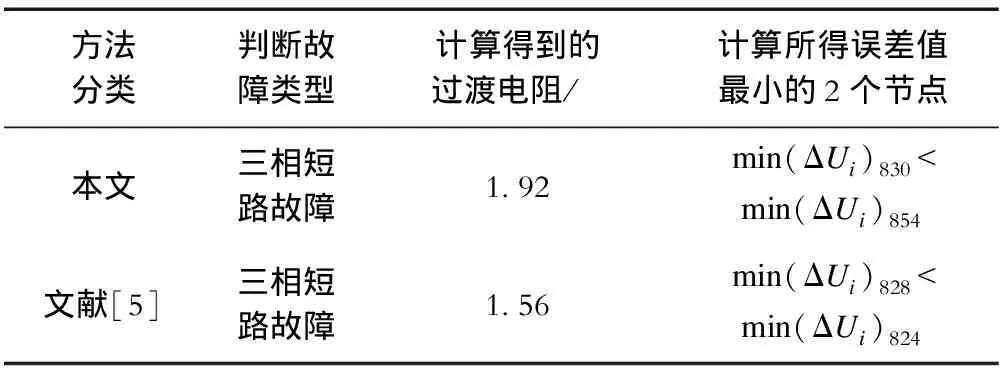
表3 方案A的故障定位结果Tab.3 Fault location results of scheme A

表 4 方案B的故障定位结果Tab.4 Fault location results of scheme B

从表3和表4中看出，当f2点发生故障时，通过本文定位算法得到离故障点最近的节点是830，第二近的节点是854，说明故障点位于节点830和854之间且靠近节点830的地方；当f3点发生故障时，通过本文定位算法得到离故障点最近的节点是854，第二近的节点是852，说明故障点位于节点854和852之间靠近节点854的地方，上述计算结果与仿真设置基本吻合；另一方面，采用基于文献[5]中的DFIG短路电流计算方法的故障定位结果与仿真设置相差较远，说明DFIG短路电流计算的误差使得最终定位的误差也较大。

根据方案B的要求，要求将故障定位于1 km以内。上文中已经将故障锁定为节点854和852之间靠近节点854的地方，进行进一步的定位。

根据前文所述，节点854和852之间的距离L为11.2 km，此时新的节点数应为12个，节点间距l=1 km。在上文中得到的结果显示，故障地点更靠近于节点854，因此，为了简化计算，确定有效节点数为7个，分别是节点854和线路854-852上与节点854相距1 km、2 km、3 km、4 km、5 km、6 km的节点。

与第3节基于搜索使计算结果和仿真结果最接近的节点的方法一样，对新的7个节点进行进一步的搜索，得到的使得min(ΔUi)最小的2个节点为线路854-852上与节点854相距4 km和相距5 km的节点，即确定故障位于线路854-852上与节点854相距4 km和5 km 两点之间，至此，故障被定位于1 km的范围内。显然，若需要将故障定位于更小范围内，在理论上只需进一步选择新的节点，可以将故障锁定于所需的范围。