基于实时最大功率估计的光伏系统参与电网调频的控制策略

徐放，钟诚，王昱博

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2. 国网吉林省电力有限公司检修公司，吉林 长春 130041)

随着化石能源的枯竭以及环境的恶化，可再生能源的需求量不断增大，新能源发电在电力系统中占据着越来越大的比重[1-6]。光伏电源通常采用电力电子逆变器并入电网，存在非线性特性明显、缺少惯性等不足，当系统由于负荷变化造成频率不稳定时，不具备对电网的频率支撑能力[7]。2015年7月，国家发改委、能源局颁布的《关于促进智能电网发展的指导意见》[10]明确指出：“将推广具有即插即用、友好并网特点的并网设备，满足新能源、分布式电源广泛接入要求。”在上述背景下，如何保证高比例光伏电源接入电网成为了重要的问题。

目前使光伏系统参与电网调频的方法主要有光-储联合发电系统和光伏减载运行[11-14]，本文关注后一类方法。

文献[15]推导了不同光伏渗透率下的功率波动概率模型，优化了同步发电机参数，实现了发电机功率控制与频率调节，但是并未使光伏系统参与一次调频。文献[16]提出对光伏电站采用功率差值的控制方式，设定光伏电站的减载水平和功频静态特性，使光伏参与一次调频，但是并未给出光伏最大可用功率的具体估算方法。文献[17]通过仿真，验证了大型光伏电站通过减载参与电网调频可以改善系统的频率响应，但是未涉及具体光伏逆变器减载控制策略。文献[18]提出基于减载控制的光伏调频策略，通过离线拟合与在线功率跟踪相结合，提高减载控制的容错性，但是只对单峰值功率曲线进行了设计。文献[19]提出了一种分层控制方法，通过限制有功功率输出来参与频率调节，但并未涉及二次调频。

本文提出一种基于实时最大功率估计的光伏系统参与电网调频的控制策略，应用一种新型控制功率输出方案，并与拟合估计的最大功率相结合，依据电网频率的变化来调整减载率，使光伏系统参与电网的一次调频和二次调频。最后，通过算例仿真对所提控制策略的有效性进行验证。

1 整体控制策略

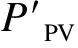
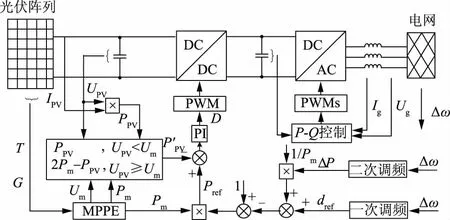
MPPE—最大功率点估计，maximum power point estimation的缩写；PWM—脉冲宽度调制，pulse width modulation的缩写。

图1 整体控制策略
Fig.1 Overall control strategy

本文的控制策略主要分为功率控制和频率控制2个部分。

功率控制主要是利用MPPE方法，根据变化的温度和辐照度实时得到光伏输出的最大功率，并与在线功率跟踪相结合来调整光伏发电机组的输出功率，经PI调节得到占空比D，从而调节直流电压。DC-DC转换器调整输出电压，同时逆变器执行电压控制并使用P-Q(有功功率-无功功率)控制算法将功率传输到电网。

频率控制分为一次调频与二次调频控制。一次调频控制主要是根据频率的变化调节减载率，达到调节有功功率输出的目的，从而使光伏发电机组拥有与传统同步发电机组类似的调频响应。二次调频是由自动发电控制(automatic generation control，AGC)模块来调度控制的，主要根据同步发电机转子速度偏差经由PI调节来控制输出功率，从而达到调频的效果。

本文所提控制策略的核心为不同状况下系统的调频能力。因此，在仿真验证中考虑多种情形，如不同光伏渗透率、不同下垂与惯性系数及负载突变等。

2 功率控制策略

2.1 基于温度和辐照度的实时MPPE

光伏模块由许多串联和并联连接的光伏电池组成，每个串联串长度相等。同样，光伏阵列由许多串联和并联连接的光伏模块组成，每个串联串长度相等。因此，假设光伏阵列没有阴影，其I-U(电流-电压)曲线也可以采用相同的方式估算，其中电压和电流分别根据串联和并联的单元总数来缩放。

参考文献[20]，本文选用二次多项式来估计最大功率，即Pmp=f(G,T)。根据G和T的数值，通过计算线性回归方程(1)来得到最大功率。

Pmp=d+a1T+a2T2+b1G+b2G2+cTG.

(1)

式中d、a1、a2、b1、b2、c均为拟合参数。

2.2 光伏阵列离线模型

本文光伏阵列模型采用5参数的单二极管模型(如图2所示)，该模型具有较高的拟合精度[21]。输出电流的计算见式(2)。

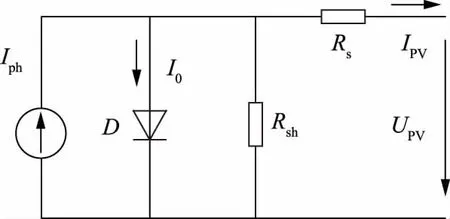
图2 光伏电池等效电路Fig.2 Equivalent circuit of photovoltaic cell

(2)

式中：Iph为光生电流；I0为二极管反向饱和电流；Rs为串联电阻；Rsh为并联电阻。

在光伏电池板方面，本文选择SunPower公司的SPR-305E-WHT-D型光伏电池进行离线数据分析，其参数见表1。光伏电池P-U(有功功率-电压)曲线如图3所示。

表1 单个光伏电池板关键参数Tab.1 Key parameters of a single photovoltaic panel

图3 光伏电池P-U曲线Fig.3 P-U curves of photovoltaic cell

2.3 拟合参数的确定

离线拟合的过程如图4所示，其中下标“i、j”表示每一组测量值，下标“k”表示运算次数。

图4 离线计算MPPE参数的流程Fig.4 Flowchart for offline calculation of MPPE parameters

流程中的第2步生成变量(Gi，Tj)对应的矩阵X，该矩阵X包含预期在实际情况下整体温度和辐照度的范围值，即

(3)

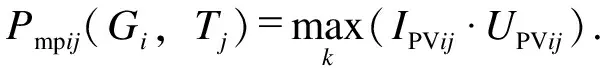
(4)

令

(5)

式(3)—(5)中：Tmax、Tmin分别为测量温度的最大值和最小值；Gmax、Gmin分别为辐照度的最大值和最小值。

在离线过程的最后一步中，根据式(4)和(5)，通过求解线性回归问题Pmp=X1β中的β来找到式(1)的拟合参数。其中βT=[da1a2b1b2c]。拟合参数见表2。

将表2的拟合参数值代入式(1)，选取几个特定的温度和光照条件，与SPR-305E-WHT-D型光伏电池实际的最大功率进行对比，结果见表3。

表2 式(1)的拟合参数值Tab.2 Fitting parameter values of equation (1)

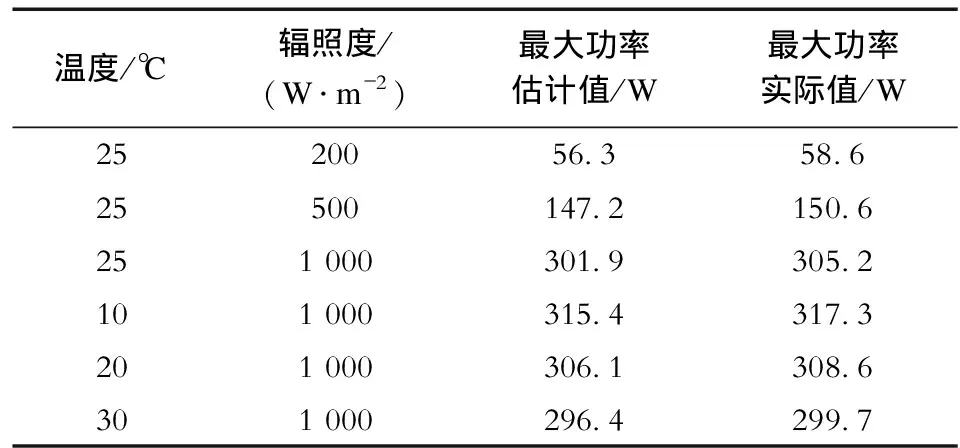
表3 最大功率估算值与实际值Tab.3 Maximum Power Estimate and Actual Value

从表3可以看出，本文计算出的最大功率估计值与实际值差异很小，说明本文方法在最大功率估计方面准确度较高。

2.4 在线功率跟踪

由图3可知，光伏电池的P-U曲线不是单调曲线，因而常规PI控制无法调节输出功率。功率控制算法原理如图5所示，当功率一定时，会对应2个电压值(工作点1和工作点2)。选择工作点2更有利于功率调节。这是因为在最大功率点(maximum power point，MPP)的右侧斜率较大，使得动态响应较快。更为重要的是，在MPP的右侧可以更容易实现功率从零到最大功率的调节。因此，本文选择将MPP左侧曲线以MPP的值为轴，通过镜像的方式形成对称曲线，从而将P-U曲线改变为单调曲线。

图5中，PI控制器不是调节实际的P-U曲线(实线)，而是调节修改后的P-U曲线(虚线)。修正后的光伏发电功率

(6)

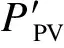
3 频率控制策略

3.1 光伏一次调频控制方式

第2节已经讨论了最大功率估计算法，通过将主动减载与下垂和虚拟惯性控制结合的方式，可实现光伏系统参与电网一次调频。参考文献[22]，本文设计的频率响应控制策略如图6所示，f0为额定频率，kd为下垂系数，ki为惯性系数，d0为初始减载率，减载率参考值dref作为下一层控制的参考输入。

图6 频率响应控制策略Fig.6 Frequency response control strategy

图6中，ki通常取2倍的虚拟惯性时间常数Hvir，而常规发电机组的惯性时间常数为2～6 s，本文选取Hvir=2 s。

与常规发电机组类比，下垂系数kd的倒数为调差系数R，即R=/kd。R取值范围通常为2%～5%，本文选取R=2%，即kd=50。需要指出的是，kd取值大小与光伏初始减载率d0相关。初始减载率与频率偏差Δf的静态关系曲线如图7所示，Pmpp为最大功率估计值，Δfmax为电网运行允许的最大频率偏差。

根据图7，当电网处于频率下限时，光伏发电系统应输出最大功率，即

(7)

通常电力系统允许的频率偏差为±0.2 Hz。取kd=50，则由式(7)易知d0=20%。即，电网频率为额定值时，光伏系统输出功率为最大跟踪功率的80%。

3.2 光伏二次调频控制方式

本文构建的模型为小型电网，因此采用AGC方式来进行二次调频。二次调频控制的简化模型如图8所示。由图8可知，AGC指令由一个延时模块控制，根据系统实际运行情况发送指令。经由PI调节过后得到的功率差值ΔP反馈输入到各发电机组中来进行频率控制。由于AGC控制为整体调度控制，因此功率差值ΔP如何分配到每个机组是关键问题。参考文献[23]，功率差值ΔP可以按照每个发电机额定输出功率占总发电功率的比例来进行分配，在图8中表示为ΔP1和ΔP2。

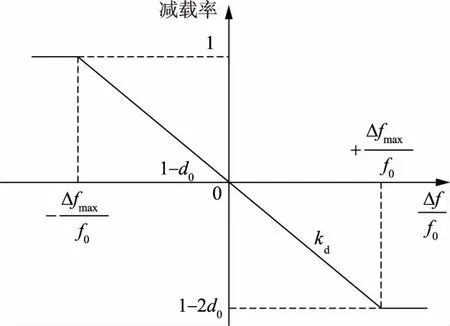
图7 初始减载率与频率偏差的静态关系曲线Fig.7 Static relation curve between d0-Δf

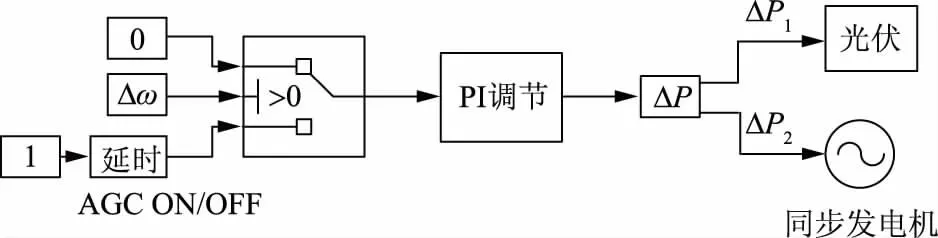
图8 二次调频控制的简化模型Fig.8 Simplified model of secondary frequency modulation

4 仿真算例分析

4.1 光伏减载算法验证

本文所采用的单个光伏电池板的关键参数见表1。暂时不考虑图1中的频率控制，减载控制层的减载率参考值dref通过外部直接给定。

本文设计场景中，外部环境温度T以1 ℃/s的速率变化，实际辐照度G以30 W/(m2·s)速率变化。减载模型算法验证结果如图9所示。

对比给定减载率曲线、实际辐照度曲线和实际光伏输出功率曲线可知，当模型精确时，本文方法可以较为准确地跟踪给定减载率，实现光伏变减载率运行。

4.2 不同光伏渗透率下光伏系统参与电网调频响应

为分析所提控制策略参与电网调频的效果，本文采用图10所示的小型独立电网进行仿真验证。该电网包含1台光伏发电系统和2台同步发电机，同时向负载供电。根据图1的控制策略，初始负载是一个有功功率为800 MW的三相RLC(电阻-电感-电容)负载(感性无功功率为200 Mvar，容性无功功率为187 Mvar)和一个-200 Mvar的容性负载。

图9 减载模型算法验证结果Fig.9 Verification result of load shedding model algorithm

图10 小型独立电网结构Fig.10 Small independent grid structure

参考文献[24]，同步发电机的简化模型如图11所示，其中s为拉普拉斯算子，ud,abc为同步发电机输出电压，TSM为调速器调节积分时间常数，TD为原动机调节积分时间常数，Uf为励磁电压。同步发电机利用自身的调速系统进行一次调频，并由统一的AGC调度参与电网二次调频，其重要参数见表4。

图11 同步发电机简化模型Fig.11 Simplified synchronous generator model

/MW900/kV20/Hz608

本节对不同渗透率的光伏系统参与电网调频的效果进行评估，假定光伏发电的额定输出功率分别为100 MW、200 MW和500 MW。为验证图1控制策略的有效性，在负荷端增加一个经三相断路器连接的160 MW感性负载，并让断路器在t=50 s时断路，来模拟负载突变时系统的调频能力。不同光伏渗透率下的系统响应曲线如图12所示。

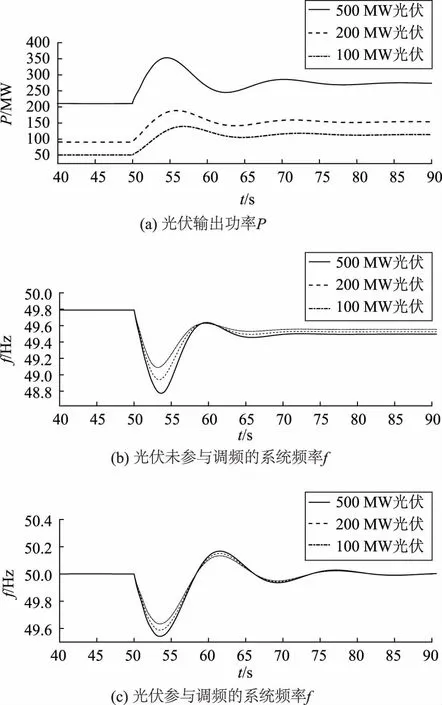
图12 不同光伏渗透率下的系统响应曲线Fig.12 System response curves under different photovoltaic permeability

从图12可看出，在负载突变的情况下，随着光伏渗透率的增大，在光伏不参与调频时，系统频率会有一定的偏移。应用本文所提的调频控制策略，频率偏移得到明显改善。另外，不论在光伏渗透率高或是低的状况下，调频效果并无明显的变化。

4.3 下垂系数和惯性系数的影响

为了讨论下垂系数和惯性系数对调频效果的影响，需要针对不同的系数值进行分析。取不同下垂系数kd的值，仿真结果如图13所示；取不同惯性系数ki的值，仿真结果如图14所示。

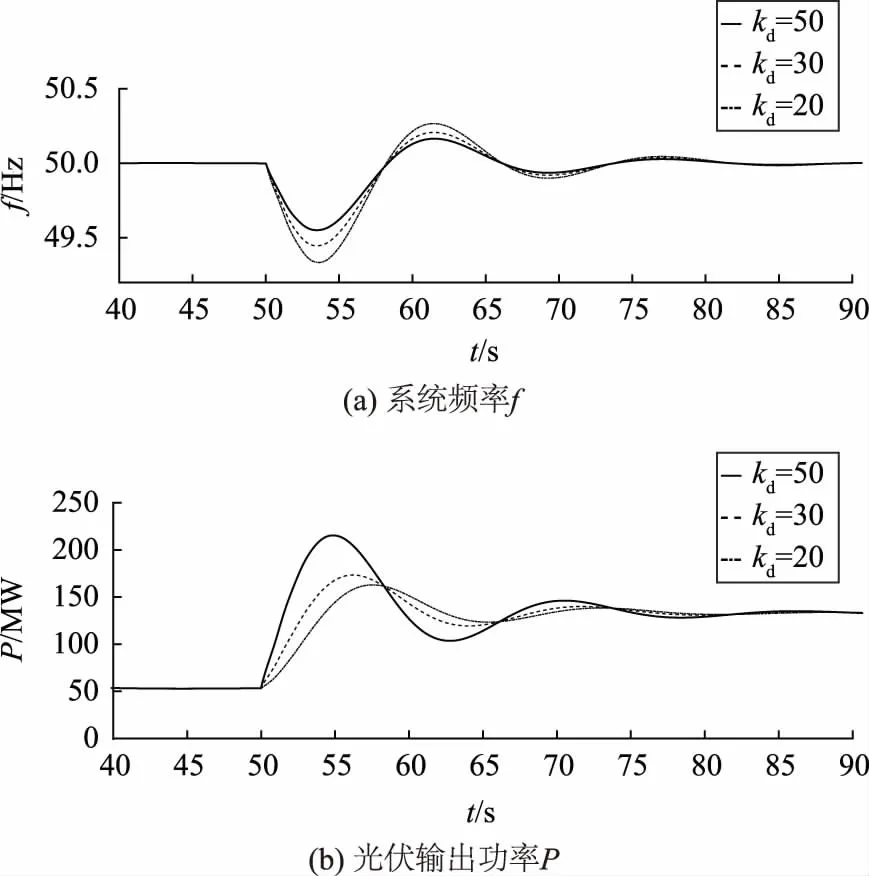
图13 不同下垂系数下的系统响应曲线Fig.13 System response curves under different droop coefficients

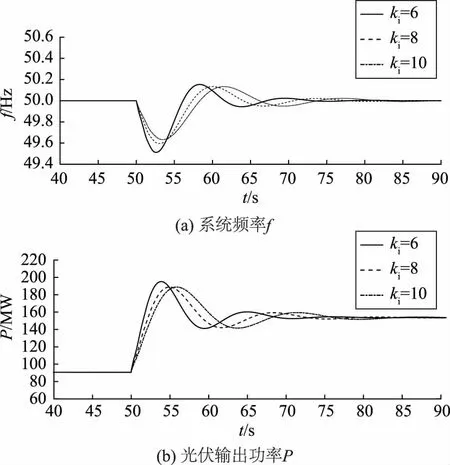
图14 不同惯性系数下的系统响应曲线Fig.14 System response curves under different inertia coefficients

由图13可知，增大下垂系数，可使光伏发电对系统频率控制的贡献增大，从而减小频率的波动；由图14可知，增大惯性系数，可以有效地减少系统频率的偏移，同时减小光伏输出的波动。

5 结束语

本文提出一种基于实时最大功率估计的光伏系统参与电网频率调节的控制方法，该控制方法通过离线拟合，能够在温度和辐照度变化的情况下准确地估计光伏最大功率，并能根据电网频率的变化调整减载率，使光伏发电系统能够自适应地调节输出功率，从而使光伏系统能参与电网一次调频和二次调频。仿真结果验证了在不同光伏渗透率及不同调频参数情况下该控制策略的有效性。