低信噪比下短波授时信号的去噪方法研究∗

谢亮

(中国科学院国家授时中心西安710600)

1 引言

时间频率保障体系是一个国家重要战略资源的基础设施.全方位、全空间的立体授时网络,是保证国家时频体系安全、可靠的重要手段.20世纪60年代,国家从战略需求考虑,在陕西省蒲城县建成我国第1个专用无线电授时台,呼号为BPM,自1981年正式承担我国标准时间、标准频率的短波授时服务.短波授时主要依靠天波反射,不受网络枢纽和有源中继体制约,信号传播距离远并且其传播信道具有其他授时手段无法比拟的战时抗毁性.特别是在卫星信号微弱的地区,短波授时能够发挥其独特优势.

短波授时信号采用常规双边带调幅的方式,自身抗干扰能力差.另外,电离层的复杂性、恒变性导致短波信道是一个复杂的、典型的频率选择性衰落信道.多径干扰、各种形式的电台以及突发形式的大气噪声等因素都会对BPM短波时号产生极大的干扰.因此,针对短波信号的特点,研究适合于短波信号的滤波方法,对于提高短波授时的可靠性和提高短波授时精度具有极其重要的作用.

对于短波授时信号的检测,常用的方法为谱减法、短时能量检测法、谱熵法等,这些信号处理方法通常假设背景噪声是平稳的,对于平稳噪声往往效果很明显,但并不适用于非平稳的噪声情况.由于短波通信中产生的噪声分布特性不同于高斯白噪声,因此,采用这些方法来处理短波噪声往往效果很差,特别是在信噪比小于0 dB时往往没有效果,这样就严重影响了短波授时信号的定时精度.针对短波授时信号背景噪声的特点,文章采用希尔伯特-黄变换(HHT)算法从带噪信号本身构造基函数进行分解,通过筛选固有模态分量从而滤除部分不包含短波时号的噪声,再通过合成便得到预处理之后的短波授时信号,谱减法是传统处理语音信号背景噪声方法中最常用的方法,两者相结合可以更好地抑制短波通信噪声,提高信号输出信噪比.

2 BPM短波授时信号编码方式

国家授时中心BPM短波授时信号采用双边带幅度调制的方式.协调世界时(UTC)信号采用1 kHz正弦信号的10个周波去调制载频信号,产生长度为10 ms的音频信号,世界时(UT1)以同样的方式产生100 ms的音频信号.整分信号、UTC和UT1均采用1 kHz正弦信号的300个周波去调制载频信号,产生长度为300 ms的音频信号,秒信号和分信号的起始点分别为音频信号第1个周波的起始点,信号格式如图1所示.

图1 BPM秒信号及整分信号格式Fig.1 The format of BPM second signal and minute signal

为适应时频技术的快速发展以及提高短波授时服务水平,国家授时中心在现有5 MHz载频增发短波时码,内容为年、月、日、时、分、秒、UT1改正值和闰秒警告.发播程序是在UTC时号中插入以125 Hz副载波调制的时间信息码,时码脉冲起始沿滞后于UTC秒起始沿20 ms[1].

BPM发播程序如图2所示,以30 min为一个周期,每个周期共播发20 min UTC (分两个时段)、4 min UT1、5 min载波(标准频率)、1 min电台呼号,以2.5 MHz、5 MHz、10 MHz、15 MHz交替发播,以保证低载频的照明区覆盖高载频的寂静区,相互补充,确保短波授时信号的国土全覆盖.

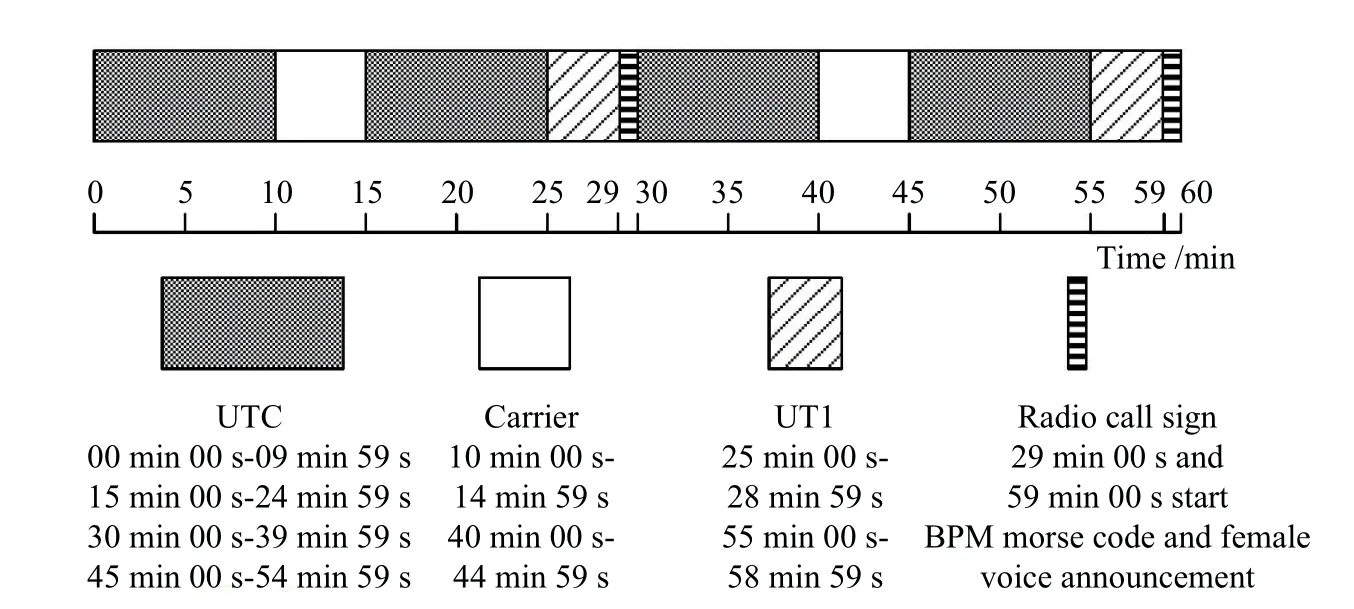
图2 BPM时号发播程序Fig.2 The broadcasting program of BPM time signal

3 希尔伯特-黄变换(HHT)及改进型谱减算法分析

希尔伯特-黄变换(HHT)是一种将经验模式分解(EMD)和希尔伯特谱分析(HSA)结合起来的算法,是一种专门用于分析非线性和非平稳过程数据的自适应方法[2].HHT的关键是EMD,任何复杂的数据都可以被分解成有限的固有模态函数(IMF).该分解过程是对非平稳信号的一个平稳化处理过程,通过迭代过程将信号中不同尺度的信号按照频率从高频到低频分解出来[3].这种方法具有自适应性,从信号处理的角度看,EMD分解类似于一个自适应带通滤波器,IMF则表示不同带宽的滤波器对信号进行自适应滤波以后的结果.

3.1 经验模态分解(EMD)算法

经验模态分解过程属于连续筛选过程,该过程主要目的是消除叠加波以使数据波形更加对称,通过EMD分解出来的IMF必须满足以下两个条件[4]:

(1)对于分量信号,极值点和过零点数目必须相等或至多相差一个;

(2)对于信号中的任意采样点,上下包络由极大值和极小值确定,且均值为零.对于条件(1),类似于传统平稳高斯过程对于窄带信号的定义,条件(2)将传统的全局限定变成了局部限定,主要是为了减少瞬时频率的波动.分解过程如下.首先,求出带分解信号x(t)的所有极值点,采用3次样条拟合函数得到信号的上下包络线,对上下包络线做均值处理得到x(t)的均值m1(t),将原始数据序列x(t)与m1(t)相减得到新的序列h1(t).其次,判断h1(t)是否满足IMF的两个条件,如果满足则为分解出的第1个固有模态分量IMF; 如果不满足,则将h1(t)作为新的起始信号,重复之前的分解方法直到满足IMF条件为止.最后,将满足条件的hk(t)作为第1个IMF分量c1(t),该分量是x(t)中频率最高的成分.将x(t)与c1(t)做差得到余量信号,重复之前的分解过程将会得到不同IMF,如(1)式所示:

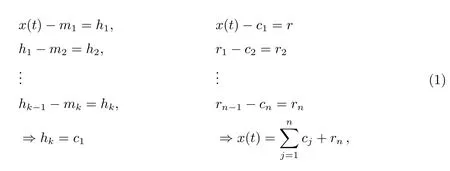
其中,x(t)表示需要处理的信号,cj表示分解得到的IMF分量,rn表示余量.

EMD算法将非平稳信号分解为不同频率及趋势项之和,通过迭代过程,将信号的局部特征进行筛选得到信号中频率最高的分量,再以同样的方式,层层筛选,最后得到信号周期大于信号持续时间的频率成分,也是最小频率,这个成分被称为趋势项,也是停止筛选的标志.

由于EMD分解算法是按照信号的特征时间尺度进行分解,随着固有模态分量阶数的不断增加,相应分解分量的特征尺度也会增大,表现在频谱上就是信号按照高频到低频顺序滤波.但是当信号时间尺度有阶跃变化时,该算法就会出现模态混叠的问题,表现在固有模态中就是多个IMF中包含相同的频率成分.

图3所示为通过全波段收音机录制的带噪短波BPM时号经过EMD分解得到的固有模态分量IMF (取前8个IMF分量).可以看出,经过EMD分解,带噪短波时号被分解后的固有模态分量IMF,其波动性从上到下逐步减小,即频率从高频到低频不断变化,虽然存在模态混叠,但是频率变化的趋势没有改变.

图3 带噪短波时号EMD分解Fig.3 The decomposition of EMD for the short-wave time signal with noise

3.2 改进型谱减算法

谱减法是语音信号处理的一种常用方法,主要表现在频域降噪.其基本思想是假定噪声和语音信号相互独立,从带噪信号的功率谱中去除噪声的功率谱,从而得到较为纯净的语音信号频谱.该方法物理意义明确、约束条件少、运算量小,因此应用较为广泛.

假设带噪语音信号的时域表达式为:

其中,y(t)表示带噪语音信号,d(t)表示纯净语音信号,n(t)为加性噪声,则相应的频域表达式可以表示为:

其中,Y(ω)、D(ω)、N(ω)分别为y(t)、d(t)、n(t)的傅里叶变化,由于d(t)、n(t)互不相关,故有:

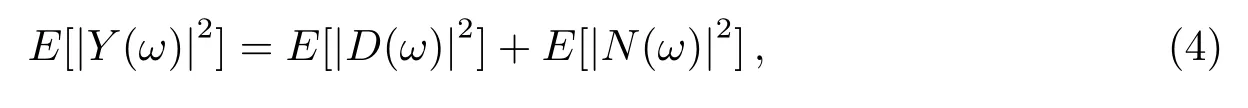
其中E[∗]表示统计平均值,E[|N(ω)|2]可以通过对语音信号进行端点检测,通过语音信号“静寂时段”的统计平均值得出,因而原始信号的语音幅度谱估计值可表示为:

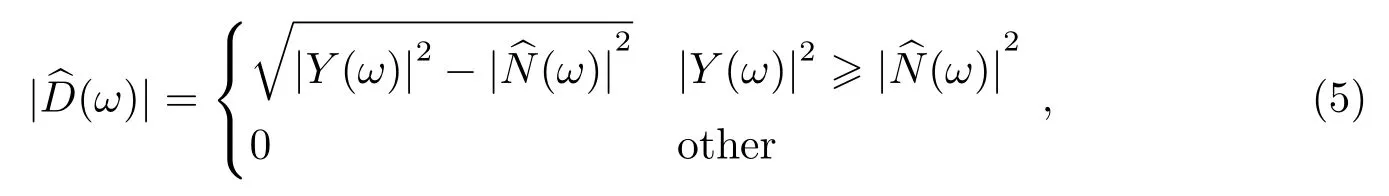
这种传统的谱减法有一个缺点就是估计噪音的时候简单采用统计平均的方法得到噪音估计值.对于带噪信号,噪音的强度相对于噪音平均值有大有小,这就造成谱减后会有

残留的噪音存在,这种残存噪声称之为音乐噪声.

为解决音乐噪声的问题,对传统的谱减法进行了改进,增加过减因子α和频谱下限阈值参数β(0<β <1).令α>1,则相较于传统谱减法有更强的滤波效果,通过调整β的值使得谱减后幅值小于β|(ω)|的值统一为该固定值,从而减小音乐噪声的影响,该固定值也是宽带噪声,通过调整β来调整宽带的噪声强度,通常α的值根据音频帧的信噪比来确定,表达式为:

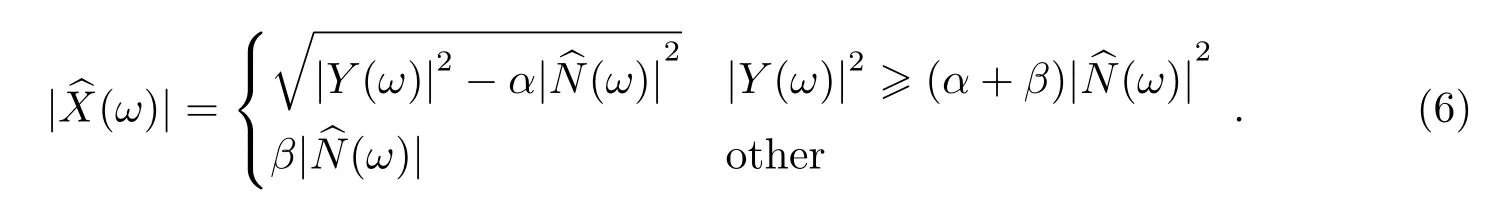
4 基于经验模态分解及谱减法的短波时号去噪算法

对于平稳的正弦信号,其频谱可以通过傅里叶变换得到,对于平稳的非正弦信号,其频率可以表示为若干正弦信号的合成,通过对合成信号进行傅里叶变换,从而得到信号的频谱.

短波时号是由1 kHz正弦波的不同时长表示标准时间的秒信号和分信号,时码信号同样采用125 Hz正弦波作为副载波,通过不同的时长表示不同的时间信息.纯净的短波时号和时码是平稳的正弦信号,但是由于短波的传播特性,电离层的影响会使短波时号出现色散、吸收、衰落、多普勒频移、干扰等各种不确定因素而呈现随机变化,这些随机变化导致无法使用示波器定时法确定时号秒起点[5].因此,这种随机变化的带噪短波时号具有非平稳特性.

HHT分析方法中,EMD分解算法从带噪语音信号本身构造基函数,可避免事先选择基函数带来的麻烦以及固定基函数和信号不匹配所产生的新噪声.通过自适应分解,将带噪信号分解为固有模态分量之和,每个固有模态分量与具有纯净短波时号频率信息的正弦波进行相关性检测,选择具有短波时号频率信息的IMF并求和,得到含有近似高斯白噪声的含噪短波时号,最后利用改进后的谱减法进行语音增强,达到对短波时号的滤波,原理如图4所示.

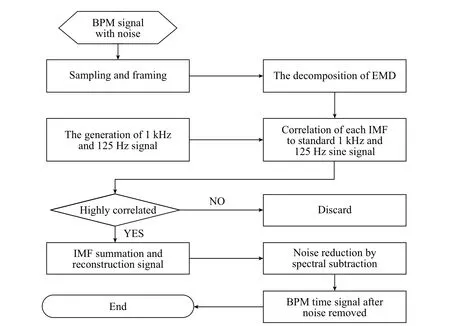
图4 基于EMD和谱减法的短波时号滤波原理图Fig.4 The schematic diagram for the short-wave time signal noise reduction based on the EMD and spectrum subtraction

5 实验结果

由于短波通信噪音的频谱分布特性不同于高斯白噪声,为更加真实地表现滤波效果,本论文带噪短波时号采用全波段德生收音机采集,原始带噪短波时号信噪比约为−8 dB,为证明本文方法的优越性,实验中引入其他滤波去噪检测算法进行实验结果比较.

图5从上到下依次为原始带噪短波信号、谱减法去噪后的短波信号、短时谱熵法短波时号端点检测结果、短时能零法短波时号端点检测结果和EMD+谱减法去噪后的短波信号.由于短波时号长度为10 ms,而实验结果长度为3 s,因而无法完整显示短波时号波形,为更好地说明实验效果,图5中最后一幅图对EMD+谱减法语音增强之后的一个短波时号进行了放大,以直观地显示滤波后的短波时号调制波形.可以看出短波时号的幅度时大时小,这是由于电离层的双折射和随机起伏特性以及电离层的不均匀结构导致短波时号的幅度出现衰落现象而产生.

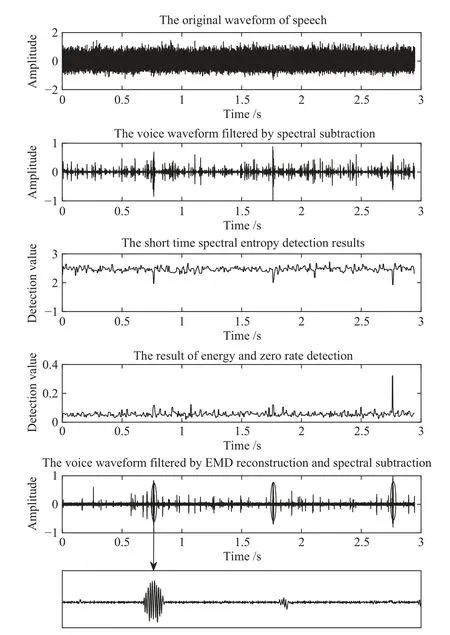
图5 多种滤波算法滤波效果比较图Fig.5 The comparison of filtering effects for multiple filtering algorithms

从图5可以看出,采用谱减法和短时能零法进行短波时号的端点检测在输入信号信噪比为−8 dB的情况下几乎失效.谱熵法有一定的效果,滤波之后的信噪比约为0 dB,采用本文所采用的算法,滤波之后的信噪比为2.3297 dB.实验结果表明,基于EMD分解及谱减法的短波时号去噪算法在滤波效果方面相较于常用的谱减法、谱熵法、短时能零法等信号处理方法在从短波通信噪声中提取短波时号时具有一定优势.

6 结论

文章根据短波时号的特点,采用非平稳信号处理方法与平稳信号处理方法相结合的语音处理算法,对带噪短波时号首先采用EMD经验模态分解算法进行自适应分解,再根据最大相似性选择需要处理的固有模态分量IMF进行语音信号重构,最后通过改进型的谱减算法进行滤波得到增强后的短波时号.该算法的输入信号采用普通短波收音机采集,这样仿真效果更加接近实际情况.通过实验结果可以看出,该算法能够大幅提高输入带噪短波时号的信噪比,提高使用短波时号定时的精度.