一种GCRS下Λ型双向频率传输的高精度相对论模型∗
2019-06-20程然韩文标何克亮
程然 韩文标 何克亮
(1 中国科学院上海天文台上海200030)
(2 中国科学院大学北京100049)
(3 中国空间技术研究院西安分院西安710100)
1 引言
现今高精度时频信号主要来源于原子钟,人们利用将原子钟放置在卫星上的方法来获得原子与微波或光信号间更长的作用时间,以进一步实现原子钟频率稳定度的提高[1].上世纪末,欧洲航天局(ESA)就提出了空间原子钟组(ACES)任务,计划将一台激光冷原子铯钟(PHARAO)和一台空间主动型氢钟(SHM)搭载于国际空间站(ISS)上,利用分布于全球的地面高精度原子钟网络,建立空间钟与地面钟间的超高精度时间频率传递链路,实现高精度时频信号的产生以及传递[2].在该任务里,利用产生高精度时频信号的原子钟组,在进行时频传递实验中,频率不确定度预计达到10−16量级,频率稳定度预计达到10−16量级(天稳),并通过激光比对链路使地面钟时间比对精确度达到50 ps水平.在其后续计划空间光钟(SOC)任务当中,由于空间钟将采用光晶格钟,时钟的频率不确定度预计达到10−17[1].这样的高精度时间频率比对链路,一方面可以用于基础物理实验,如检验引力红移、研究基本常数的时变特性以及验证局域不变原理等; 另一方面,则可以开展如地面原子钟间高精度时间频率传递、相对论重力测量、地球遥感和大气时延等科学应用[3].近年来我国也在筹备基于载人空间站的空间原子钟项目,并考虑在外太空建立时间频率实验室,采用锶光钟、铷喷泉钟、主动型氢钟共同组建空间原子钟钟组:高精密时频基准通过高精度的微波和激光链路向地面和空间传递时间和频率,对传递链路时间稳定度的要求高达ps量级,原子钟组增加光钟之后,日稳定度和不确定度有望达到10−18量级,相比较ACES任务,时间频率信号的频率稳定度和准确度将提高1个量级以上[1],而如何令其服务于已开展的相关研究项目已成为我国实现自主研发所面临的重要任务之一.
然而受到引力红移的影响,地球附近信号收发位置1 m高程的变化都会在时间频率传递过程中产生10−16大小的频移; 信号在传播过程中收发点的相对运动所导致的多普勒频移又会受到时间膨胀效应以及引力时延的影响,在地面站与ISS间的时频传递过程中,仅地球扁率的引力时延效应所引起的多普勒频移就已经达到10−17.显然在进行超高精度时间频率传递实验中以牛顿力学为基础的理论模型已无法满足人们对于频率不确定度和稳定度等的要求,这就要求我们必须在广义相对论框架下实现时频传递链路的数据处理; 进一步,应用地心天球参考系(GCRS)的坐标时给出空间原子钟原时与地面原子钟原时之差的计算(等同于给出频移的计算).
国际上最早关于相对论框架下时钟频率比对的理论分析由Jaffe和Vessot给出,该理论分析涉及对二阶引力红移的相关计算(尽管计算到c−3精度,但是没有考虑由于引力时延引起光线切矢的变化对于多普勒频移的影响,同时关于收发台站运动也没有按照c−3精度进行处理,因此不是严格的c−3精度),其结果已应用到引力探测器A(GP-A)实验以及GPS系统当中并得到验证[4]; 随着时钟稳定性的提升与双向时间传递方案和定常轨道激光同步方案的提出,包含更高阶项的更精确的理论处理由Petit、Klioner等人在其相应的工作中完成[5−6]; 目前国际上对高精度时频传递相对论模型的研究,主要是针对ACES进行的建模,因为研究对象为地球引力场作用范围内的人造天体,因此模型采用的参考系为GCRS,其中Blanchet等人在2001年给出了c−3精度下的时频传递理论模型,该模型在频率传递中考虑了球对称引力场下一阶和二阶多普勒效应、爱因斯坦引力红移、夏皮罗时延以及光线切矢受引力场的影响,根据ACES的科学需求,模型忽略了地球的自转、质量四极矩和日月的潮汐势等,时间传递模型精度为1 ps,频率比对模型的精度为10−17[7]; 后来他们基于孤立、轴对称旋转体引力场又将该模型推广至c−4精度,进一步考虑了引力红移中地球自转、质量四极矩对时间频率传递的影响,应用时间传递函数(TTF)方法考察引力时延对频移的影响从而极大简化了计算,并在c−4精度下包含了Nordvedt-Will后牛顿参数,不过该模型仅局限于单向时频传递[8].
国内目前已公开的与空间原子钟时频传递相关的相对论效应研究中,早期较有代表性的工作有陕西天文台(现国家授时中心)有关研究人员在地固系下针对在准确度和稳定度达10−13量级的时频测量中需要考虑的相对论效应所进行的相关介绍[9]; 到了近10 yr,紫金山天文台有关研究人员针对质心天球参考系(BCRS)提出了修正的标量-张量-矢量引力理论(MSTVG),并根据该理论在参数化二阶后牛顿(2pN)精度下给出了含四极场和引力磁效应的光行时公式、光传播频移公式及相关量级估计[10]; 华中科技大学有关研究人员针对GCRS在具有潮汐、轴对称和旋转的引力场下系统地给出了关于时频传递的相对论模型[11]; 此外,上海天文台、南京大学、国防科技大学等单位针对太阳系内的高精度天文、测距、时间同步等技术的相对论模型都开展了系统、深入的研究[1,12–17].目前,我国的时频传递项目急需的理论模型,还在研究过程中.由于我国时频项目的设计精度要求高于ACES,相对论模型精度要求也高于国外同类模型.
本文考虑到目前国际、国内的研究基础和现状,将影响量级在10−18的效应也考虑进来,给出高精度的时频传递链路理论模型,并针对地球附近轨道高度400 km左右的近地轨道卫星(LEO)与地面之间的时频传递以及中地球轨道(MEO)卫星与地球静止轨道(GEO)卫星之间的信号时频传递给出了相应的处理模型.内容安排如下: 在2.1节中,本文将对第24届国际天文学联合会(IAU)提出的IAU2000决议当中有关一阶后牛顿天文参考系的内容作简单介绍; 在2.2节中先对后牛顿极限下的单向频率传递的现有理论模型进行论述,再在IAU2000决议确定的参考系下给出指定精度下单向频率传递的另一种理论模型; 2.3节在此基础上进一步给出Λ频率传递链路的频差计算模型并且根据地面-LEO和MEO-GEO两个例子对定轨精度、卫星转发间隔等技术指标给出约束条件;最后在第3节中将对本文的内容进行总结,并对所建模型进行探讨.本文中如无特殊声明,c均代表真空中光的传播速度,G代表引力常量,并且约定指标中罗马字母指代1、2、3,希腊字母指代0、1、2、3.
2 时频传递中的相对论效应分析
2.1 IAU2000有关相对论参考系的决议简介
基于本文所涉及到的时间频率传递实验是在地球附近的引力场时空背景下进行,因此我们选择地心天球坐标系(GCRS),根据IAU2000关于天文参考系的决议,GCRS中的度规张量具有如下一阶后牛顿(1pN)形式[18]:
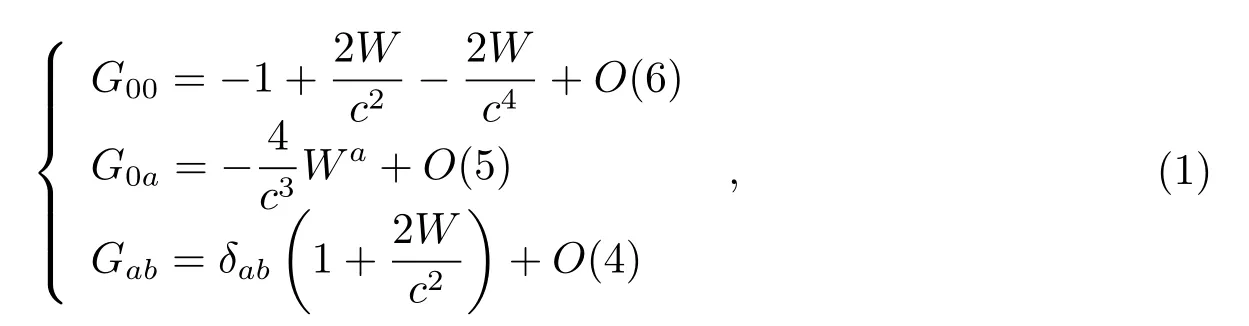
其中G00、G0a和Gab是度规张量的各个分量,O(n)表示O(c−n),δab是克罗内克符号,并且a,b= 1、2、3.这里W和Wa分别是引力的标量势和矢量势,是空间坐标X和坐标时间T的函数,它们可以分为自势和外势两部分,具体说明详见IAU2000决议的相关介绍[18],为便于后面的相关讨论,下面仅对由地球质量分布引起的自引力势作相关说明.在IAU2000决议B1.4中关于该标量位势采用了类似于牛顿力学下的多极展开,即
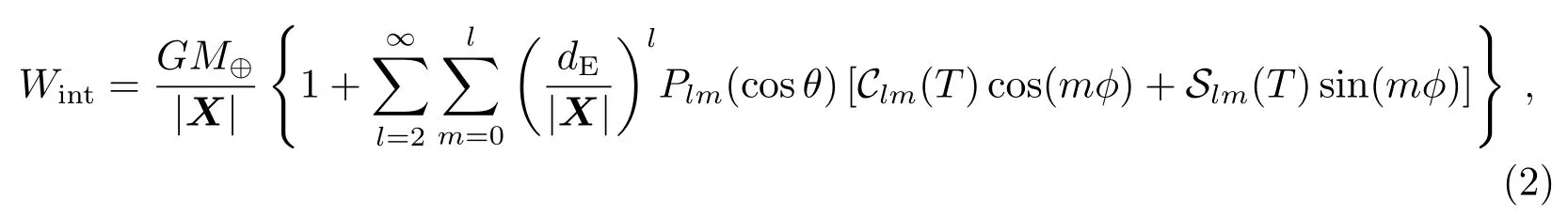
其中Plm是缔和勒让德多项式,Slm和Clm在一定精度下等价于Damour等人引入的后牛顿多极矩[19],可通过对基于国际地球参考架(ITRF)的EGM08重力场模型进行坐标变换得到[20],M⊕是地球质量,dE是地球半径,θ和ϕ为对应于GCRS中空间坐标Xa的角坐标.有一点需指出,由于上式为GCRS下的展开式,因此即使忽略章动、极移和岁差等因素对地球自转的长期影响以及潮汐形变效应,Slm和Clm依旧为随时间变化的量,且公共周期约为1 d.
基于IAU2000决议中关于相对论参考系的描述,我们可以对地球附近的信号时频传递实验进行相应的理论建模.
2.2 时频传递模型
在频率传递过程中的观测量是信号接收和发射时的频率比νR/νE(在光线传递过程中,我们将发射事件记为E,接收事件记为R,下同),该量便于应用于时钟频率比对等科研任务,体现在: 一方面,通过本地频率转换,可以间接获得时钟频率比对,即另一方面,可以与依赖坐标的量建立较为简洁的关系.下面我们首先介绍光线传输过程中频率偏移的一般形式[8],即

其中lµ是对应事件中光线的切矢分量,uµ和vi分别是发射事件中发射源(或者接收事件中接收源)的四速度分量和坐标速度分量,表达式中采用爱因斯坦求和约定: 重复指标代表求和.这样,通过建立坐标量lµ、uµ和观测量νR/νE之间的联系,并把坐标依赖的实际记录数据和观测量建立关系,从而建立完整自洽的数据处理模型.(3)式中,和即描述了坐标时与固有时之间的关系,比式u0R/u0E主要包含了引力红移以及部分二阶多普勒频移,而比式则主要反映了在选定参考系中引力延迟影响下的一阶多普勒频移,下面将分别对这两个比式进行相应分析与估计.
表1 /中各影响因素对于频移的影响量级(以LEO-地面站、GEO-MEO间频率传递为例,选取的LEO轨道高度为400 km,MEO轨道高度为21528 km,GEO轨道高度为36000 km)Table 1 The magnitude of the influence from each factor related to u0R/u0E on the frequency shift (in the cases of time transfer for LEO-ground and GEO-MEO,the altitude for LEO,MEO,and GEO is 400 km,21528 km,and 36000 km,respectively)
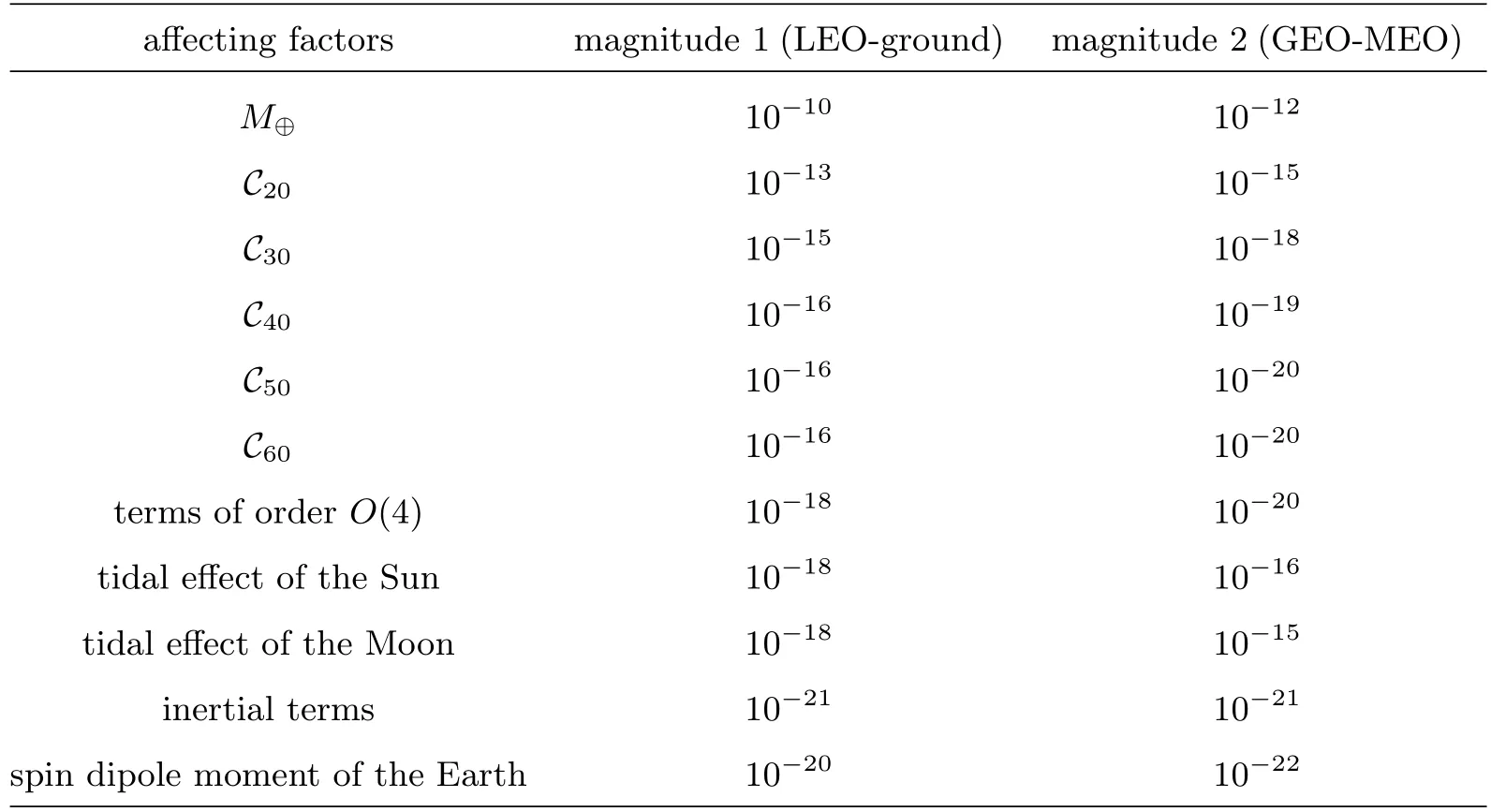
表1 /中各影响因素对于频移的影响量级(以LEO-地面站、GEO-MEO间频率传递为例,选取的LEO轨道高度为400 km,MEO轨道高度为21528 km,GEO轨道高度为36000 km)Table 1 The magnitude of the influence from each factor related to u0R/u0E on the frequency shift (in the cases of time transfer for LEO-ground and GEO-MEO,the altitude for LEO,MEO,and GEO is 400 km,21528 km,and 36000 km,respectively)
affecting factorsmagnitude 1(LEO-ground)magnitude 2(GEO-MEO)10−1010−12 C2010−1310−15 C3010−1510−18 C4010−1610−19 C5010−1610−20 C6010−1610−20 terms of order O(4)10−1810−20 tidal effect of the Sun10−1810−16 tidal effect of the Moon10−1810−15 inertial terms10−2110−21 spin dipole moment of the Earth10−2010−22 M⊕
通过对时间传递函数(TTF)[8,21]求梯度与光线切矢建立数学联系,可以为计算背景参考系下的相对论性多普勒频移提供理论依据[8].关于比式(c+livi)R/(c+livi)E中地球质量、地球质量四极矩、自旋、潮汐项和惯性项引力时延(分别记作TM,l=0,TM,l=2,TS,l=1,TT,l=2和TI)对应的切矢分量,经计算可以得到[17](见附录),各部分所引起多普勒频移的影响量级如表2所示,对于表中未列出的四极矩部分(C22和S22等)的频移影响在10−19量级.
对于10−18的频移精度要求,不需要考虑更高阶质量多极矩的影响[8],这里不再一一列出.因此,时延部分只需考虑质量以及质量四极矩部分.
需要说明的是,这里所给出关于时延部分影响的结论仅在单次测量且引力场为稳态场时有效.单次测量时间约为0.1 s,信号传播过程中,引力场其实产生了微小变化.分析发现这种假设仍然保证了频率传递精度为10−18.首先是对自转进行考察,对(2)式展开到l=2可以发现,在GCRS中Slm和Clm不因坐标起算点ϕ0发生变化的只有C20,考虑到质量四极矩Mij非主对角线分量(主要对应于S22和C22)相对于主对角线元素(主要对应于C20)要低2−3个量级[17],而地球自转时所产生的引力场时变效应则主要源于这些田谐项和扇谐项,于是当考虑引力势的时变性后,通过在计算TT,l=2中应用积分中值定理,并在此基础上重复附录(1.17)式的推导过程,可估计对于单次时频传递中由于自转所产生的引力场时变效应对频移的影响量级∼10−24,因此在应用TTF中可以忽略不计.
接下来,我们对岁差、极移、章动等因素所引起地轴偏移进行分析.由于单次频率传递的坐标时间间隔∆t ∼0.1 s,考虑岁差等因素后经估算可知Mij的变化不会超过C20的10−12,而根据附录中(1.17)式可知只要Mij的变化不超过C20的10−2即可满足精度要求,因此引起光线偏折的地轴偏移部分对频率的影响完全可以忽略.至于潮汐效应,根据对附录中的(1.21)式的计算可知潮汐势时延对频率的影响远小于10−18,由此单次测量中潮汐引入的时变性也可忽略不计.此处,由于(3)式本身是基于稳态场假设给出的,对比文献[11]中基于非稳态场假设给出的(14)式并依上文中的类似分析可估计出(3)式其模型误差量级在10−20水平.以上论证即说明了即使在10−18频率不确定度水平上,单次测量情况下,利用TTF计算频率传递中引力场的光线偏折效应时,不需要考虑引力场的变化.不同的测量时,引力场的变化自然包含进了引力势的计算中,我们无需稳态引力场假设.
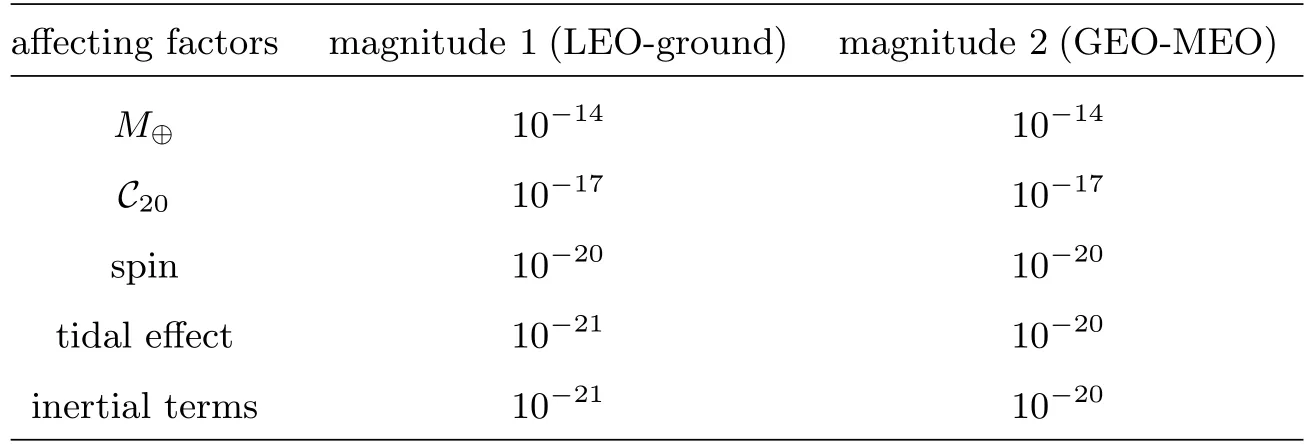
表2 引力作用下各因素引起的光线偏折对于频移的影响量级(以LEO-地面站、GEO-MEO间频率传递为例,选取的LEO轨道高度为400 km,MEO轨道高度为21528 km,GEO轨道高度为36000 km)Table 2 The magnitude of the effects from the gravity-induced deflection of light on the frequency shift for each factor (in the cases of time transfer for LEO-ground and GEO-MEO,the altitude for LEO,MEO,and GEO is 400 km,21528 km,and 36000 km,respectively)
根据以上估计,可直接引用文献[8]中的相应结论给出频率精度为10−18的单向频率传递方程的形式.设在坐标时TE时刻,光线由位于XE、坐标速度为vE的源发出,在TR到达位于XR、坐标速度为vR的观测者,则光线接收与发出时的频率比满足
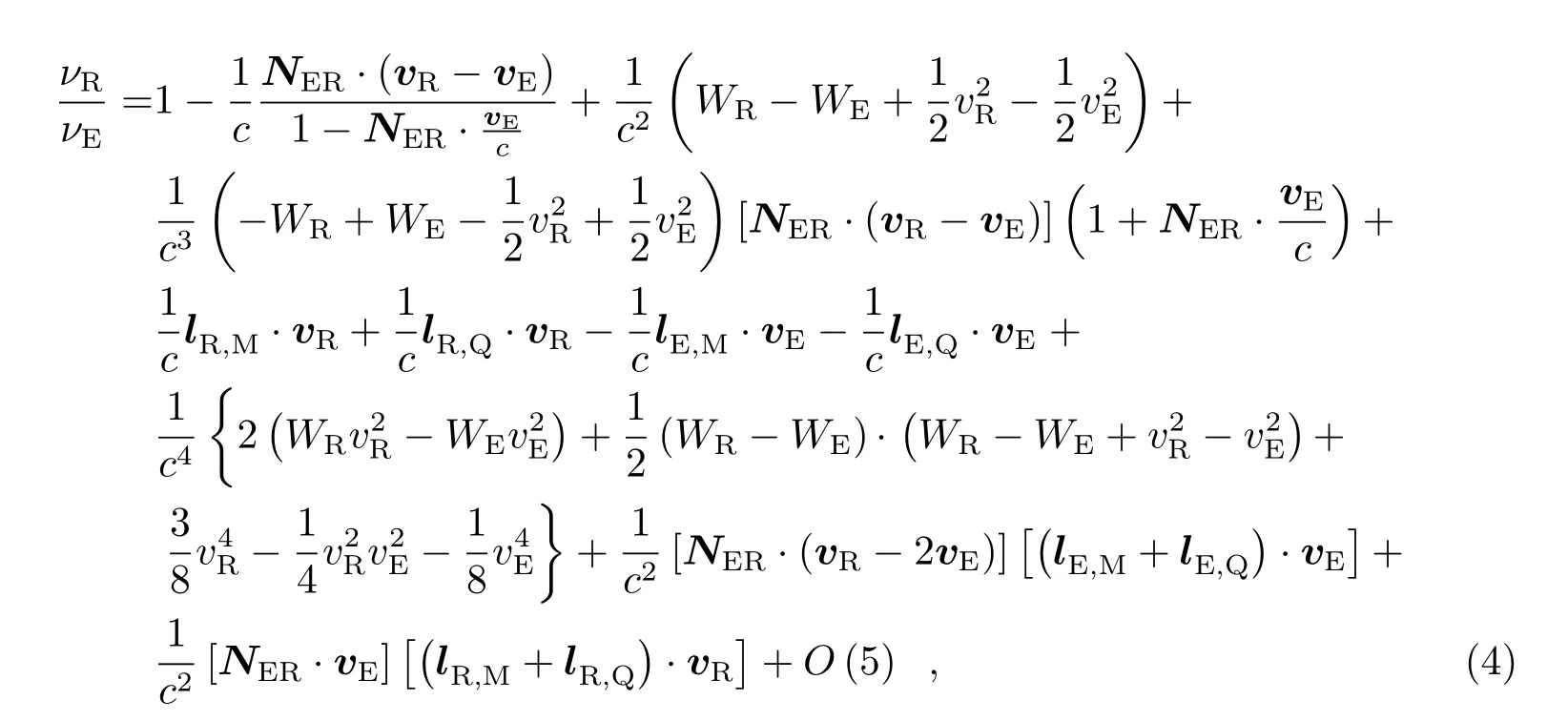
其中NER= (XR−XE)/|XR−XE|,WR和WE分别是关于(TR,XR)和(TE,XE)的势函数.而切矢中由于地球质量引起的部分lE,M、lR,M以及由于地球质量四极矩引起的部分lE,Q、lE,Q,其具体形式详见附录中(1.15)–(1.18)式.
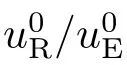
以上就是我们针对观测量νR/νE所作的分析,为了便于计算,我们分别考虑了构成νR/νE的两个比式(c+livi)R/(c+livi)E和的所有影响因素,从而实现了不确定度达10−18的观测量理论处理模型.相比较Linet等[8]基于孤立、轴对称旋转体系给出的处理模型,我们的模型采用了IAU2000决议确立的天文参考系,因此在地球附近有着更好的适用性,而且频率精度设计在10−18,要高于ACES任务的频率精度要求(10−16).但是也需要注意,由于海平面高度的变化以及质量分布不规则等因素所造成的模型误差依旧会高于设计精度.
需要强调,在每次频率传递过程中(∆t ∼0.1 s),地球引力势、外部天体方位、台站位置、卫星位置等参量在GCRS下都会发生变化,而在频率设计精度为10−18的情况下这种变化引起的频移将刚好影响到我们对于的计算结果,因此(4)式在计算中需调用对应历元下的相关参数,对于下面将涉及到的Λ型双向时频传输亦应如此分析.
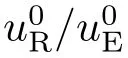
2.3 Λ链路高精度相对论模型
根据(4)式可以发现,式中包含的O(1)项是多普勒频移,这一项对频率传递实验的影响最大,于是人们通过设计Λ构型的双向时频传递链路来抵消一阶多普勒效应,提高时频传递的精度[4,7].在Λ链路中通常包含时钟一致性较好的一个信号发射源和一个信号转发源,发射源经本地时钟生成高频信号传递给转发源(该传递通道即上行链路); 转发源在接收信号的瞬间会同时向发射源处传递具有不同载波频率的信号(该传递通道即下行链路),其中有通过对接收到的发射源信号进行变频后得到的高频信号(包含不同波段)以及经转发源本地时钟生成的高频信号.信号在上行链路以及下行链路中的传递都包含着一阶多普勒频移和一些相对论频移项,综合两条链路的频移效应可构造不含一阶多普勒频移的观测量,便于对星、站进行频率比对以及对广义相对论进行验证.下面结合Λ型时频传递链路给出频移精度在10−18水平的相应计算,并对Λ链路中所允许的信号转发时间间隔进行考察.设在tB′时刻信号源发射信号,在tA′时刻信号到达中继卫星并在tA时刻由转发器再次发射信号,tB时刻信号传递到信号源位置处.在GCRS下,用XA、vA、aA(XA′、vA′、aA′)等表示tA(tA′)时刻中继卫星的矢径、速度、加速度等运动量,用XB、vB、aB(XB′、vB′、aB′)等表示tB(tB′)时刻信号发射源的矢径、速度、加速度等运动量.假设下行链路中信号接收时刻发射源的运动量以及信号转发时刻中继卫星的运动量为已知(通过信号接收时刻转发源的运动量可以得到信号转发时刻转发源的运动量,后面会说明),记R=XB−XA,R=|R|以及N=R/R,那么对于R′=XA′−XB′,利用泰勒展开到三阶项同时对时间进行迭代可得到
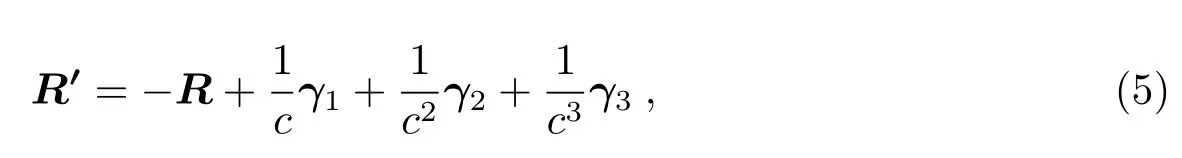
其中
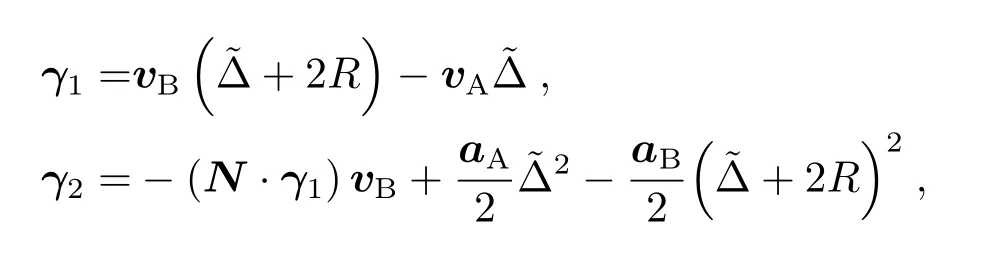

对于上行链路中发射(接收)时刻中继卫星(发射源)对应的运动速度,按照与上式相类似的处理有
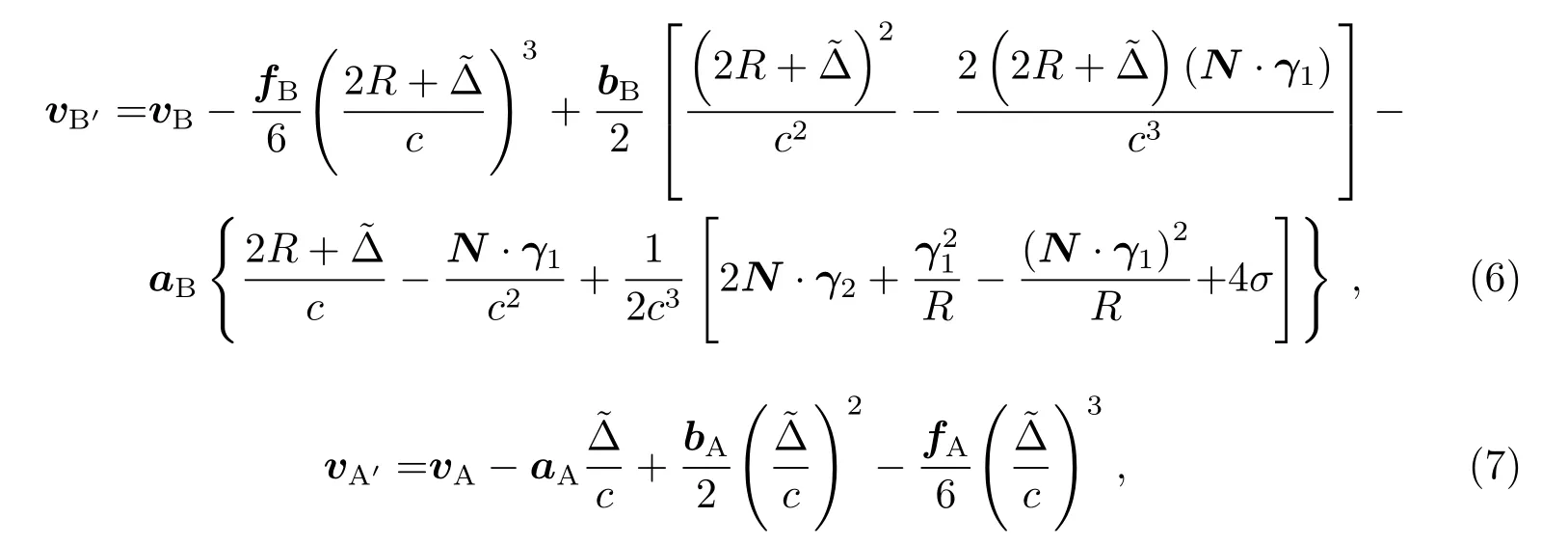
其中
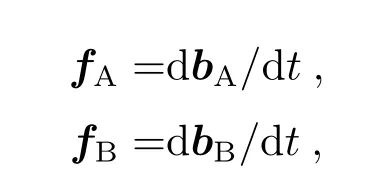
而对于N′=R′/|R′|,有

由于存在转发间隔,因此转发过程需在考虑转发卫星运动的前提下对信号的“收”和“发”两个点事件进行描述.此外,我们还考察了引力时延对于传播路径产生的影响.以上各个量都是计算到O(3)精度,代入到频移方程中则可以对上行链路的频移计算到O(4)精度.对于Λ链路,为了计算频移,通常构造如下观测量[7]
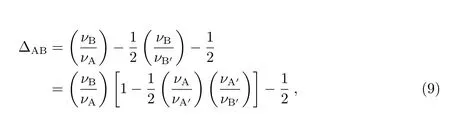
式中νB/νA和νA′/νB′分别代表下行链路和上行链路信号收发的频率比.通过在发射源处对νB/νB′进行测量来间接得到νB/νA,而∆AB则由理论计算给出.∆AB在计算中一阶多普勒项会得到抵消,有助于分离出相对论频移项,提高频移测量精度,早期在GP-A实验中用于验证引力红移.式中νA/νA′是由转发过程中产生的收发信号频移(仪器自身产生),于是可知,当λ=νA/νA′ −1∼O(n),n>1,上式才可能用于消除链路中的一阶多普勒效应而又不引入新的一阶项(即要求λ至少满足10−10左右的量级).在下文的讨论中,我们假定νA/νA′=1.
将(4)–(8)式代入(9)式,可以在10−18频率精度下计算∆AB.考虑到实际过程中tA−tA′很小(∼ns),对于含˜∆的项仅计算到O(3)项且保留到˜∆的一次项,另外根据精度需求,O(4)项中不再考虑星、站加速度以及引力势变化等部分,有
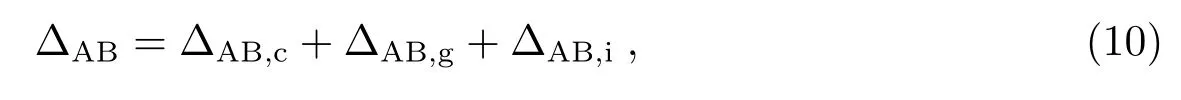
其中∆AB,c是仅与狭义相对论多普勒效应相关的部分,对于地面-LEO,∆AB,c3.3×10−10,对于地面-LEO,∆AB,c9.3×10−11; ∆AB,g是不考虑转发间隔的情况下含有引力场贡献的部分及其混合项,对于地面-LEO,∆AB,g= 4.6×10−11,对于MEO-GEO,∆AB,g= 5.4×10−11; ∆AB,i是含有转发间隔贡献的部分.对于上式的各部分所包含的Sagnac效应部分,我们不另作单独说明,记r ≡|X|,于是有rA=|XA|以及rB=|XB|,此处给出各部分具体形式:
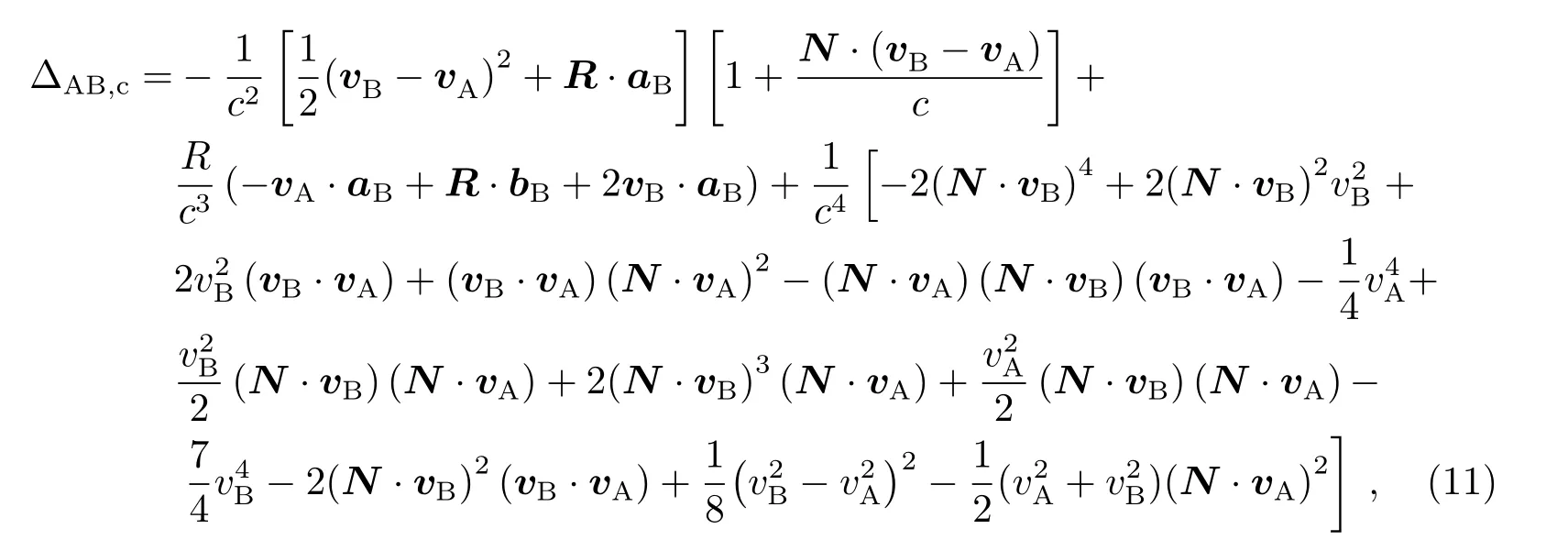
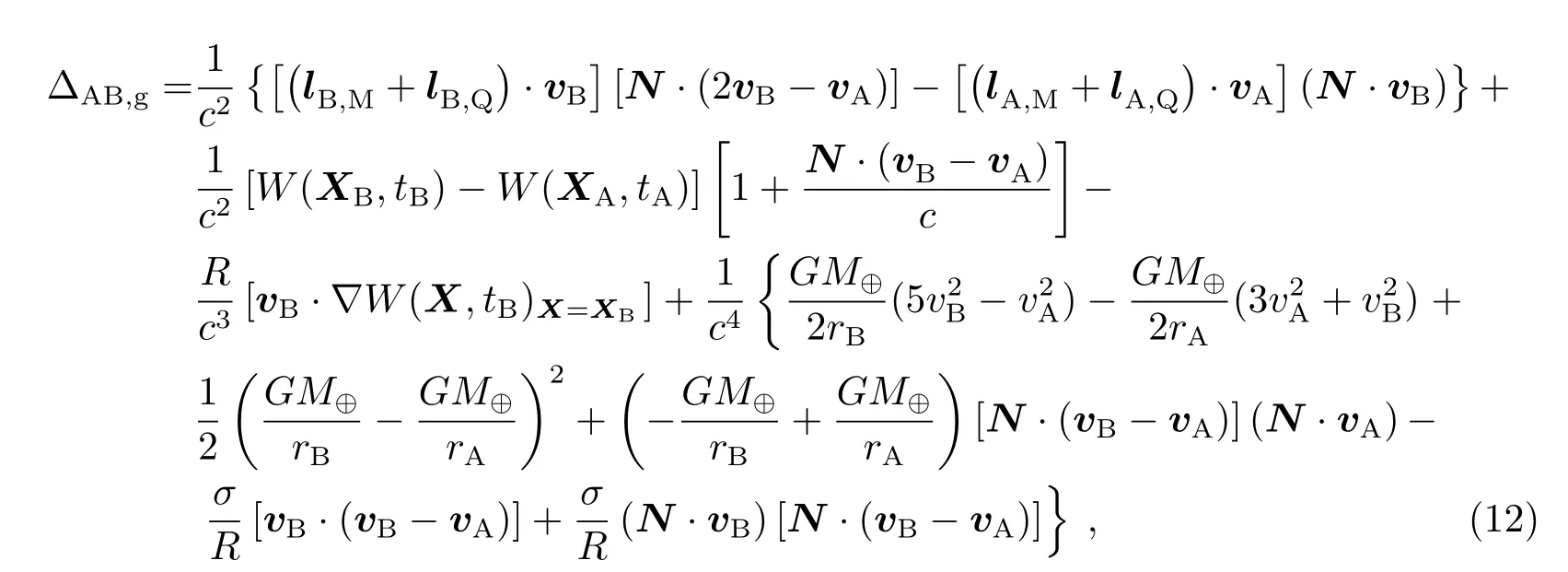
其中lB,M、lB,Q、lA,M和lA,Q分别对应于(4)式中的lR,M、lR,Q、lE,M和lE,Q,
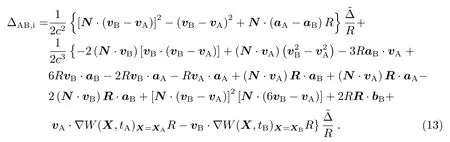
(12)式和(13)式中,在满足给定精度条件下易得
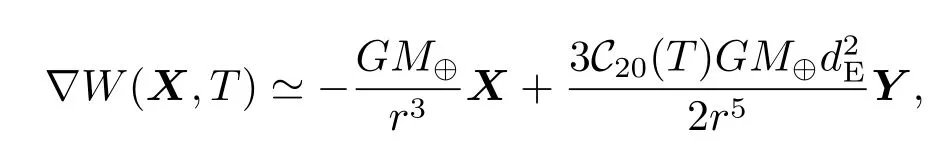
其中
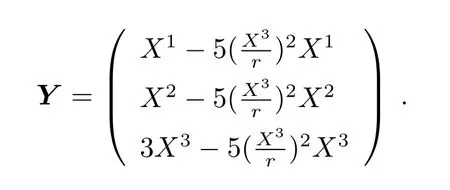
对于(11)−(13)式中tA时刻所对应的中继卫星运动状态,即式中的XA,vA,aA,下面在O(4)精度下给出相应部分计算(这里主要考虑了Sagnac效应),
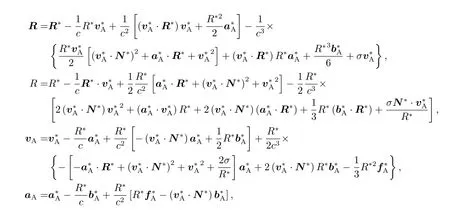
其中, 有“ * ”标记的量表示tB时刻(信号接收时刻)对应中继卫星的运动相关量,R∗=XB, 这些量是已知的,σ可以根据这些量直接进行估计[17]. 当考虑大气时延等因素后, 就可以更精确地确定以上各量以及tA(不考虑卫星运动, 则因地球自转带来的引力场时变性要求δtA<0.1 s, 因潮汐作用带来的引力场时变性要求δtA<1 s), 这里不做进一步讨论. 利用(9)式, 通过对发射源收发的频率比νB/νB′进行测量, 就可以在指定精度下得到频移的值. 由于星-站钟相对频差(这里指)的不确定度主要来源于∆AB, 我们可以从∆AB(频率)精确度的角度出发, 对定轨精度以及转发时间间隔等量进行约束, 使之满足频率不确定度在10−18的要求. 我们将速度和加速度按与方位向量垂直和平行的方向分解, 为便于给出约束, 这里只考虑到O(2)阶, 且引力势保留主要的部分, 于是有

其中
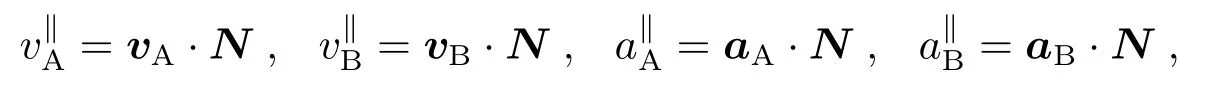
带有上标“⊥1”和“⊥2”的量和是当我们指定两个单位方向矢量P1、P2, 使得P1、P2与N两两正交时, 矢量vA分别沿P1、P2的分量, 即按照同样的方法我们给出式中和的定义. 其中关于卫星速度的这两个法向分量和, 从(14)式可以判断其偏差与径向分量偏差在同一量级, 为便于计算我们总可以指定一种指向的选择使得. 通过和可以对中继卫星径向运动、法向运动、星站距离、转发间隔偏差根据频率精度要求δν <10−18做出约束, 详见表3.
表3 在δν/ν <10−18条件下对于卫星运动偏差、台站运动偏差和转发间隔偏差的约束(以LEO-地面站、GEO-MEO间时频传递为例).表中给出的估计均假定所有事件发生在赤道面上,且中继卫星位于相对于发射源45◦高度角的情况.在取得对的保守约束时,假定了==0Table 3 Constraints on satellite movement deviation,station movement deviation,and transponding interval deviation in the condition of δν/ν <10−18 (in the cases of frequency transfer for LEO-ground and GEO-MEO).The estimations listed are given provided that all events are considered on the equatorial plane,and the relay satellite is assumed at an altitude of 45 degrees relative to the emission source.To conservatively estimate the constraint for ,we have supposed that ==0
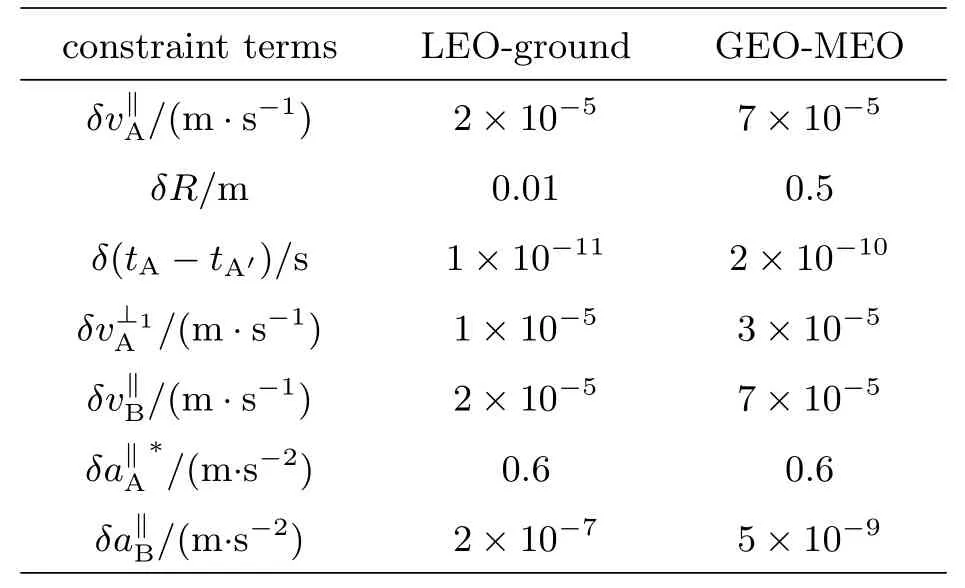
表3 在δν/ν <10−18条件下对于卫星运动偏差、台站运动偏差和转发间隔偏差的约束(以LEO-地面站、GEO-MEO间时频传递为例).表中给出的估计均假定所有事件发生在赤道面上,且中继卫星位于相对于发射源45◦高度角的情况.在取得对的保守约束时,假定了==0Table 3 Constraints on satellite movement deviation,station movement deviation,and transponding interval deviation in the condition of δν/ν <10−18 (in the cases of frequency transfer for LEO-ground and GEO-MEO).The estimations listed are given provided that all events are considered on the equatorial plane,and the relay satellite is assumed at an altitude of 45 degrees relative to the emission source.To conservatively estimate the constraint for ,we have supposed that ==0
* The estimation is given by assuming tA −tA′ =1 ns
constraint termsLEO-groundGEO-MEO δv∥A/(m·s−1)2×10−57×10−5 δR/m0.010.5 δ(tA −tA′)/s1×10−112×10−10 δv⊥1A /(m·s−1)1×10−53×10−5 δv∥B/(m·s−1)2×10−57×10−5 δa∥A∗/(m·s−2)0.60.6 δa∥B/(m·s−2)2×10−75×10−9
为了给出对转发延迟的约束,这里假设了一种理想的情况,即在转发过程中将卫星看做一个质点,受到的作用主要来自地球引力,仪器稳定性以及测量误差等忽略不计.在这样的假设下,仅提取出与转发间隔相关的项(将计算中与˜∆无关的项略去),认为转发间隔引起的频移主要是转发间隔内速度、加速度的变化引起的频移,并将轨道运动近似为圆周运动,根据(14)式有以下估计
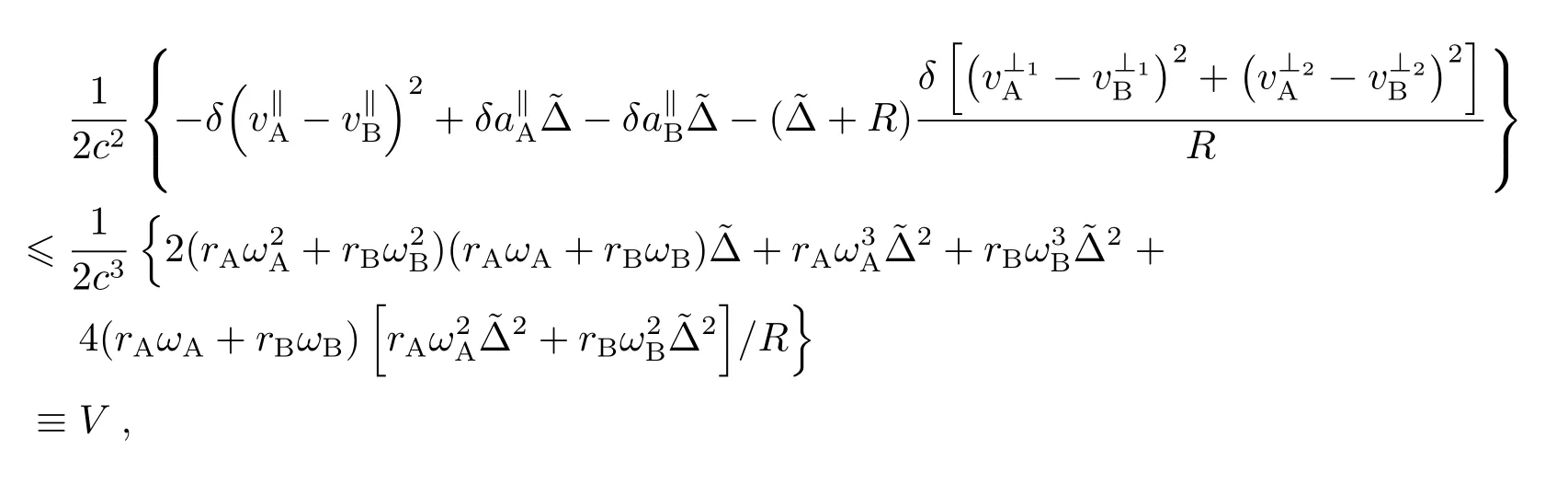
其中,ωA、ωB分别是中继卫星和发射源在坐标系中的角速度大小,令V <10−18可以得到关于转发间隔的约束(这里按照表3中的计算条件): 对于地面-LEO,有tA−tA′1.3×10−6s; 对于GEO-MEO,有tA−tA′1.7×10−5s.需要说明的是,由于以上约束是在特定条件下给出的,而且是考虑每一部分单独对频移的影响满足给定精度,所以要得到一般情况下对约束条件的保守估计,各个指标还要低1个量级左右.另一方面,Duchayne等[22]针对ACES项目中Λ构型时间传递链路的需求对卫星定轨精度和转发时延及抖动等技术指标确定了约束条件,该约束依据指定钟差精度(<0.3 ps)和频率精度(<10−16)给出,通过计算对卫星位置不确定度提出的约束在米量级,对卫星转发时延及偏差提出的约束分别在10−6s和10−7s量级,与本文完全由10−18频率精度确定的约束条件相比较可以发现,本文关于转发间隔偏差的约束远远严格于依据钟差精度<0.3 ps给出的约束.
表3中对于发射源以及转发源加速度偏差的约束其实告诉了我们引力场模型以及加速度计应该达到什么样的精度要求,从数据上可以发现在指定频率不确定度下对于发射源加速度偏差会有较强的限制,不过目前已用于地球重力场和海洋环流探测(GOCE)卫星的静电悬浮加速度计其测量频带内的分辨率为2×10−12m·s−2·Hz−1/2[23],而美国国家航天局(NASA)和欧洲航天局提出的等效原理检测卫星(STEP)计划中加速度计的设计精度为10−18g[24],其中,g为重力加速度,这将满足本文中关于加速度测量的要求.需指出,关于(11)式涉及到的转发源其加速度的一阶、二阶导数,经计算发现其偏差值的约束较为宽松,因此bA和fA相关的项可忽略不计; 关于发射源,对于地面-LEO的情况,需满足δbB1×10−6m/s3,对于MEO-GEO的情况,要求δbB1×10−9m/s3.
3 总结与讨论
由于将新一代原子钟应用于空间-地面时频传递实验中,时钟信号频率不确定度预计达到10−17乃至更高,因此我们需要在这个精度之上构建相应的时频传递模型,而这将有利于进行超高精度时间频率比对、地球遥感、大气时延研究、基本常数时变特性研究以及广义相对论验证等重要科学研究任务,对于我国开展相关研究也具有一定参考价值.而要构建这样的高精度理论模型势必要在广义相对论框架下进行考虑,基于这样的原因,本文依据IAU于2000年制定的有关相对论天文参考系的决议,在GCRS下考察了地球质量多极矩、自旋、日月潮汐势、惯性势、引力时延等因素在信号传递过程中对频移的影响量级,以频率不确定度达到10−18为目标对单向和Λ构型链路的频率涉及的相对论效应进行了分析,并且在地面-LEO和MEO-GEO两个例子中依据指定频率精度针对卫星定轨精度、转发时间间隔等技术指标给出了约束条件.
与Linet和Teyssandier在2002年提出的关于ACES任务的处理模型相比较[8],本文提出的模型要求的频移计算精度要高于ACES任务的要求,并且不是在轴对称旋转孤立体系下进行的分析,而是依据IAU2000给出的相关决议考虑了更多的影响(如潮汐效应、惯性项、非轴对称体系下引力势计算等),虽然该模型涉及到引力场的时变特性,但由于这部分对于引力延迟的影响足够小,使得我们在应用时间传递函数时可以近似视为稳态场进行处理; 此外,在考虑转发间隔的条件下对于Λ链路也依据指定精度给出了相应的处理方案.在应用该理论模型的过程中也应当注意以下两个方面: 一方面,在地面台站与卫星间时频传递过程的处理中,由于该模型不涉及地球潮汐形变的相关考虑,因此不适用于地面台站处引力势的处理; 另一方面,对于信号转发时间的约束本文采用了比较简单的处理,对于实际问题应根据具体情况进行分析.
附录
设T0时刻信号由X0处发出传播到位于X的观测者(接收信号的时刻为T),记r=为积分路径,为由原点到光线路径的垂径矢量,则对于质量多极矩、自转、潮汐势等因素构成的切矢部分如下:
(1)地球质量部分
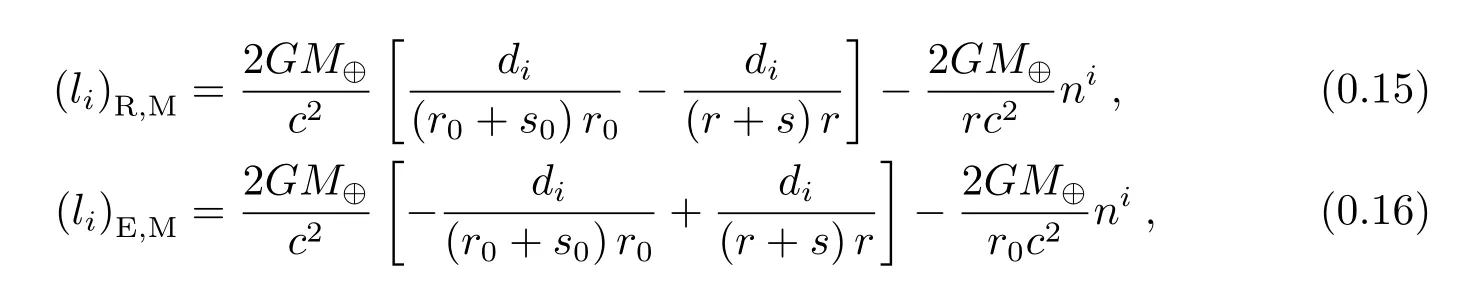
(2)地球质量四极矩部分
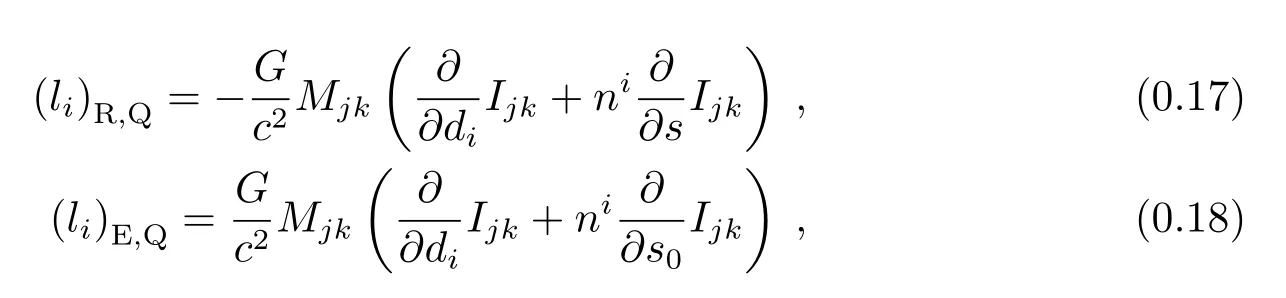
其中
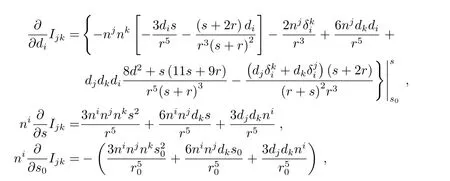
而式中的Ijk为仅与传播路径相关的量(详见文献[17]),Mjk代表地球的质量四极矩分量.
(3)地球自旋部分
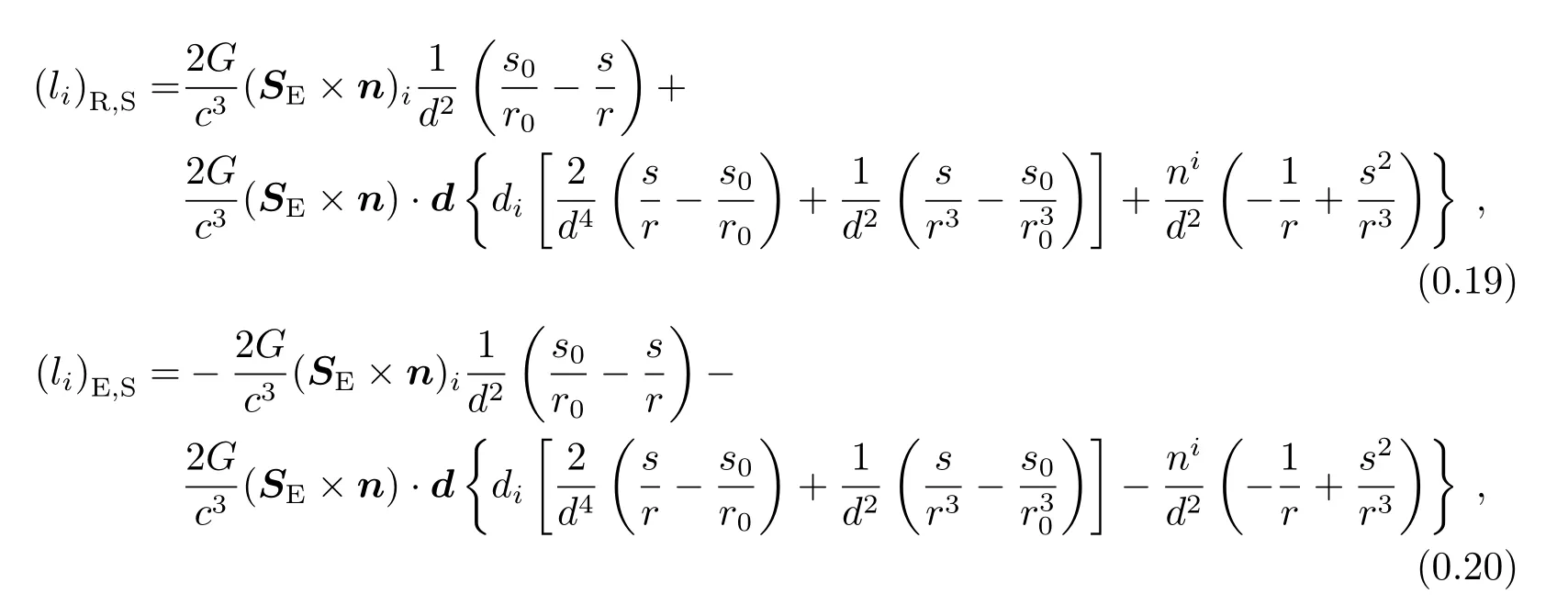
其中SE是地球的角动量矢量.
(4)潮汐项
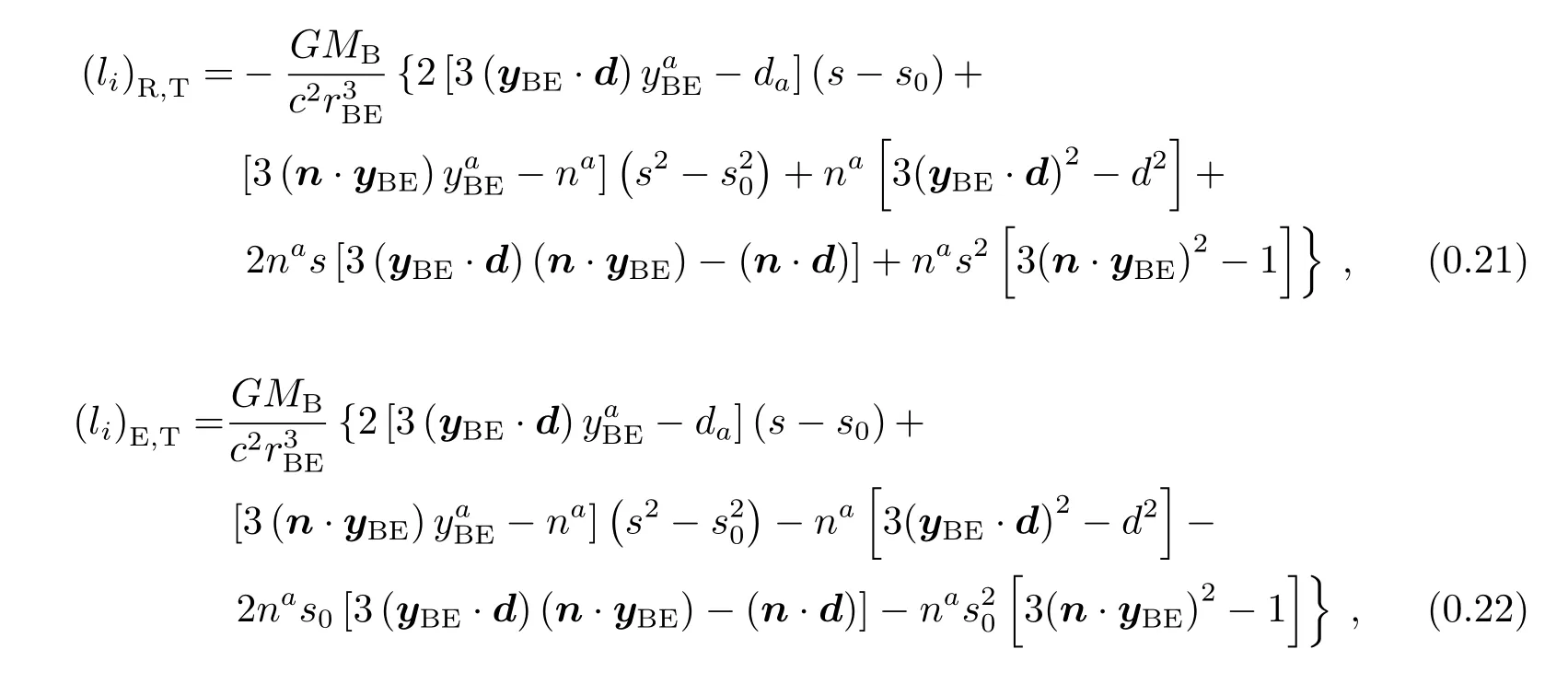
这里仅考察的最低阶的潮汐项,其中MB和rBE分别是是外部天体B的质量和它到地心的距离,yBE是由外部天体B的质心指向地心的单位方向矢量.
(5)惯性项
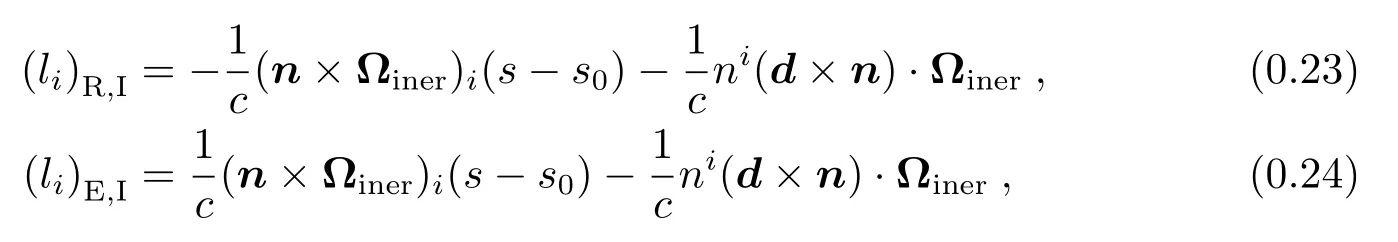
其中,Ωiner描述了由相对论科氏力引起的GCRS相对于动力学非旋转的地心参考系的旋转.
