针对不同视场辅助信标的无人机目标定位方法
2019-06-19朱惠民贾正荣王航宇孙世岩
朱惠民,贾正荣,王航宇,孙世岩
(1. 海军工程大学 兵器工程学院, 湖北 武汉 430033; 2. 中国人民解放军92941部队, 辽宁 葫芦岛 125000;3. 海军工程大学, 湖北 武汉 430033)
无人机对陆目标进行测角测距时定位精度受无人机的姿态角误差影响十分明显,且距离越远,定位精度越低。而无人机姿态估计一直都是行业内研究的热点和难点,无人机涉及六个自由度的位置估计,目前对无人机的位姿估计主要是以多传感器相结合的方式进行,如全球定位系统(Global Positioning System, GPS)、高度计、气压计、惯性测量单元(Inertial Measurement Unit,IMU)等,其中IMU是最基本的姿态测量传感器,通常用于水面舰艇、潜艇、飞机等,测量精度高,但是体积大、价格昂贵。而体积较小、重量较轻的惯性传感器,随着使用时间的推移,惯性测量误差累积将越来越大。
随着微机电系统(Micro-Electro-Mechanical System,MEMS)的发展,以陀螺仪、加速度计等惯性测量单元相结合的微机电系统惯性测量单元(Micro-Electro-Mechanical System-Inertial Measurement Unit,MEMS-IMU)目前已极其广泛地应用在诸多的小型、微型无人平台上,用以进行平台相对位姿估计。然而,MEMS-IMU对姿态的测量误差从1°/h到0.06°/min,当目标距无人机10 km时,1°的姿态角误差引起的目标定位精度误差约为(378 m×420 m×35 m)[1]。
许多学者针对基于惯性测量设备的无人平台定位问题展开了研究。Li等[2]针对GPS拒止环境中的陆地车辆精确定位问题,提出了一种结合低成本多传感器的方法,采用联合卡尔曼滤波(Federated Kalman Filter,FKF)进行信息融合,对姿态误差进行估计。Fourati等[3]为刚性运动的姿态估计提出了一种可行的四元互补观测器,在没有GPS数据的条件下进行姿态估计,可以有效地克服无迹卡尔曼滤波(Unscented Kalman Filter,UKF)的局限性。Cho等[4]针对室内传感器观测不足的问题,对IMU方向的初始预测投影进行改进,用于补偿姿态误差,并提出了一种可以检测补偿退化情况的算法。Allotta等[5]采用MEMS、IMU、磁强计以及光纤陀螺组成的多传感器单元对水下航行器(Autonomous Underwater Vehicle,AUV)的姿态进行估计,并对滤波器提出了改进方案。Barba等[6]提出了一种基于进化计算的MEMS最佳形状设计方法,针对MEMS运动在车辆、信息设备以及医疗设备上测量时产生的冲突程度提出了最小化的解决方案。此外,Guggenheim等[7]为降低制造MEMS传感器的成本,提出了一种六自由度力矩传感器设计方法,使微惯性测量单元能够被更加广泛地使用。
不仅如此,融合多传感器的姿态量测技术也逐渐在众多领域中被使用:von Marcard[8-11]等结合视觉信息,对惯性测量单元进行补偿,进行了室内环境人体结构捕捉、机器人姿态修正等;闵华松等[13]为基于RGBD-Slam的定位失败问题,在定位算法的基础上提出了结合IMU和Kinect的机器人运动状态比较与融合的姿态估计方法,利用多传感器得到的姿态估计结果构建预测模型和观测模型,提高了机器人的定位精度;马可锌等[13]提出了一种基于视觉的相对位姿估计算法,用于解决近距离的编队飞行位姿估计问题。符小卫[14-15]等对无人机用于目标定位和跟踪有了一定的研究基础,证明了无人机目标定位的可行性。
基于上述硬件发展水平和滤波算法的研究成果,本文提出一种基于光电传感器与MEMS-IMU相结合的无人机位姿求解模型,并对姿态偏差进行估计和校正,对地面目标进行精确定位。
1 问题描述
无人机空中进行搜索时,对地面场景选定一个标志性坐标点,作为辅助信标,该辅助信标的坐标精度是非常高的,既可以是战前侦察对该区域进行测量选择的制高点,也可以是通过无人机进行投放的位置信号发射器或者是地面侦查人员发射的定位信息,如图1所示。
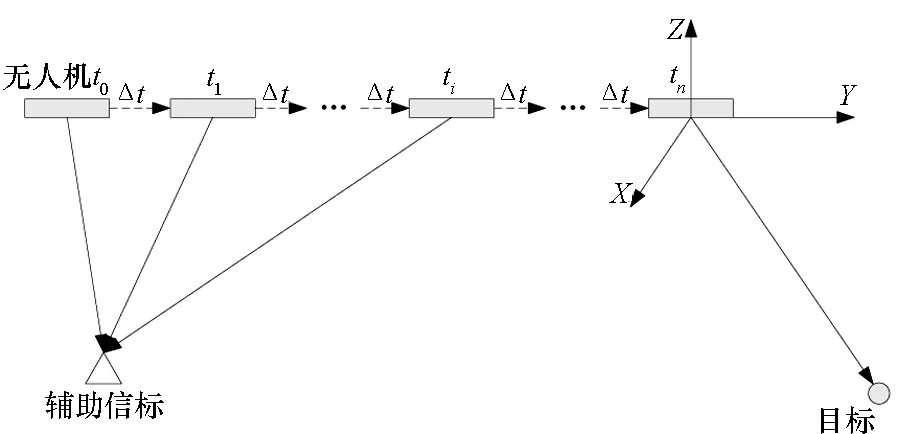
图1 基于不同视场辅助信标的目标定位作战样式Fig.1 Target location combat style based on auxiliary beacons in different field of view
采用光电传感器进行目标探测和跟踪,同时通过惯性传感器和激光传感器进行姿态的估计与更新,经过n个Δt后,无人机捕获到目标。由于前期在不停地对无人机进行姿态的校正,能够得到较为准确的目标位置。
2 无人机姿态估计方法
2.1 基于IMU的无人机姿态估计
陀螺仪输出三轴角速率,可以通过对角速率积分得到平台的姿态角信息,其特点是动态性能良好,但是精度较低,且存在常值漂移,其测量误差会随着时间漂移,不适合长时间载体姿态确定。
2.1.1 状态方程
欧拉角法具有简便直观、物理含义明确的优点,且不存在冗余参数,虽然在俯仰角为90°时存在奇异,但对无人机而言,俯仰角基本不会到达90°,因此本文采用欧拉角法对姿态运动学进行描述。取状态向量为X=(ψ,θ,φ)T,其中,ψ为偏航角、θ为俯仰角、φ为滚动角。
设陀螺仪输出的角速度为(ωb,x,ωb,y,ωb,z)T,则有:
(1)
考虑常值误差和测量噪声,式(1)变为:
(2)
式中,(v1,v2,v3)T为陀螺输出数据中的测量噪声。无人机的状态变化可以表示为:
(3)
将式(3)代入式(2),有:
(4)
式中,I为单位矩阵。
2.1.2 容积卡尔曼滤波
假设一个非线性系统:
(5)
其中,xk∈Rn为k时刻系统的状态向量,f为n维向量函数,zk∈Rm为k时刻系统的观测向量,h为m维向量函数,wk为均值为零、协方差为Qk的n维随机过程噪声,vk为均值为零、协方差为Rk的m维随机量测噪声,且wk、vk互不相关。容积卡尔曼滤波(Cubature Kalman Filter,CKF)的核心思想是通过三阶容积积分原理,计算函数的标准加权高斯积分。标准的CKF步骤如下:
步骤1:初始化。
(6)
步骤2:时间更新。
1)设k-1时刻协方差矩阵Pk-1|k-1正定,对其进行因式分解得到Sk-1|k-1,即:
(7)
2)容积点估计:
(8)
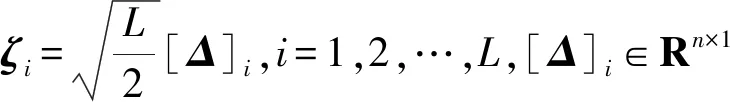
3)容积点传播:
(9)
4)求解状态一步预测值:
(10)
5)计算预测误差协方差矩阵:
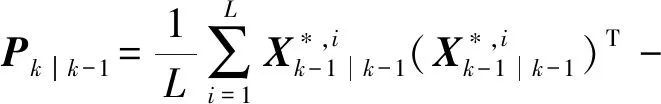
(11)
式中,Qk-1表示系统噪声协方差矩阵,Γk-1表示系统测量的估计值。
步骤3:量测更新。
1)预测误差协方差矩阵分解:
(12)
2)容积点估计:
(13)
3)容积点传播:
(14)
4)计算量测预测值:
(15)
(16)
(17)
其中,Rk表示量测噪声协方差矩阵。
步骤4:状态更新。
1)求解Kalman增益:
(18)
(19)
2.2 基于辅助信标的无人机姿态求解方法
IMU输出存在漂移,若单纯使用IMU输出进行无人机姿态估计,其精度会随时间不断恶化,因此需要借助外界信息对无人机姿态进行修正。其中,辅助信标可以通过预先信息准备选定,提供精确的绝对位置,能够用于求解无人机姿态。
当辅助信标位于无人机视场内时,无人机可以根据测得的辅助信标的相对位置,结合已知的精确辅助信标位置,对自身姿态进行求解。
在求解过程中,需要涉及三个参考坐标系,分别为载体坐标系、观测坐标系、稳定地理坐标系。其中,载体坐标系固连于无人机上,随无人机姿态改变而变化,其坐标原点即无人机质心;观测坐标系中心为无人机激光传感器的观测中心,坐标轴与载体坐标系平行,其坐标原点为传感器光学镜头焦点;稳定地理坐标系中心固连于大地上一点,以下均认为稳定地理坐标系为惯性系。
设激光传感器观测中心相对于无人机中心的位置在无人机载体坐标系内为Xoffset,p;已知辅助信标精确位置在稳定地理坐标系内的坐标为Xflag,g;无人机位置在稳定地理坐标系内为Xuav,g。
当无人机激光传感器照射辅助信标时,可以得到辅助信标相对激光传感器中心位置在观测坐标系内、以球坐标表示为(ρ,β,ε),其中ρ为辅助信标相对观测坐标系中心的距离,β为激光传感器水平角,ε为激光传感器高低角。从而可以得到辅助信标在观测坐标系内的坐标Xflag,ob=(xflag,ob,yflag,ob,zflag,ob)T,即:
(20)
对于偏航角ψ、俯仰角θ与滚动角φ的无人机,可以得到从稳定地理坐标系到无人机载体坐标系的变换矩阵Mgp(ψ,θ,φ),进而有:
Mgp(Xflag,g-Xuav,g)=Xflag,ob-Xoffset,p
(21)
在式(21)中,仅有变换矩阵Mgp未知,因此可以求解得到变换矩阵,即求解得到无人机姿态(ψ,θ,φ)。具体求解方法如下。
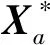
(22)
从而有:
(23)
设:
(24)
有:
MXa=Xb
(25)
其中,M由参数(ψ,θ,φ)决定,且形式为:
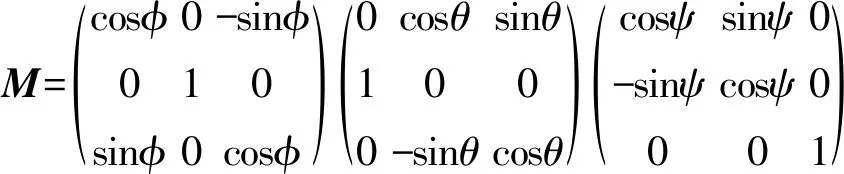
(26)
构建二次指标:
I(ψ,θ,φ)=(MXa-Xb)T(MXa-Xb)
(27)
有I(ψ,θ,φ)=0与MXa=Xb同解。然而,解析法求解I(ψ,θ,φ)=0较为困难,因而通过梯度下降法求解,有梯度:
(28)
(29)
(30)
从而构建迭代序列ξk=(ψk,θk,φk)T,有:
(31)
其中,η∈[0,1]为速率系数。给定δ>0,当
(32)
时,迭代终止,以ξk+1作为结果。
3 基于辅助信标的无人机目标定位
无人机在执行目标跟踪任务时,由于战场环境复杂、无人机视场受限、激光传感器距离受限等因素,无法保持所有时间内目标与辅助信标均位于无人机视场内,因此,无人机通过辅助信标对自身的姿态求解与对目标的跟踪一般是异步进行的,一般先观测辅助信标,后跟踪目标。当无人机跟踪目标时,只能综合当前通过IMU输出、滤波得到的姿态(以下简称滤波姿态)与之前通过辅助信标求解得到的姿态(以下简称辅助姿态)进行目标位置的求解与目标跟踪。
在滤波姿态与辅助姿态中,滤波姿态在每一时刻均能获得,但是存在一定的量测漂移,体现为无法滤波消除的系统误差;而辅助姿态虽然精度较高,但是无法在跟踪目标时同步获得。辅助姿态可以帮助估计滤波姿态的偏差,因此,拟采用基于之前得到的辅助姿态与对应滤波姿态进而估计未来滤波姿态偏差的方法,进行姿态校正。在这一过程中,涉及两个问题:一是通过辅助姿态与滤波姿态进行姿态偏差估计;二是通过姿态偏差的估计,对跟踪目标时的无人机姿态进行校正。
3.1 姿态偏差估计
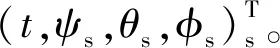
(33)
为了在无法得到辅助姿态时给出姿态差值,进而进行滤波姿态校正,需要根据Δξ的量测得到姿态偏差的规律,进而得到Tb时间之外的姿态偏差。
这里采用多项式函数对姿态差值Δξ进行拟合,得到姿态偏差估计函数。
设n阶系数向量H(t)为:
(34)
对于时间序列Tb={t1,…,tm},有系数矩阵H:
(35)
设多项式函数系数向量为Ks,Ks应满足:
HKs=Δξ
(36)

Ks=(HTH)-1HTΔξ
(37)
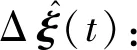
(38)
3.2 姿态校正
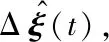
(39)
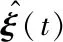
3.3 不同视场条件下的目标位置求解
通过无人机携带的图像传感器与激光传感器,无人机可以在视场中辨识目标,并对目标相对位置进行量测。通过目标位置量测值、无人机位置与无人机姿态,可以求解得到目标的绝对位置。以下分析涉及载体坐标系、观测坐标系与稳定地理坐标系。
设激光传感器观测中心相对于无人机中心的位置在无人机载体坐标系内为Xoffset,p;无人机位置在稳定地理坐标系内为Xuav,g;目标位置量测值在观测坐标系内、以球坐标表示为(ρt,βt,εt),进而得到直角坐标描述的目标位置在观测坐标系内为Xtarget,ob;ξ=(ψ,θ,φ)T为无人机姿态,进而得到从稳定地理坐标系到无人机载体坐标系的变换矩阵为Mgp(ψ,θ,φ);目标位置在稳定地理坐标系内的坐标为Xtarget,g。从而有关系:
Mgp(Xtarget,g-Xuav,g)=Xtarget,ob-Xoffset,p
(40)
进而可以解得目标位置在稳定地理坐标系内坐标为:
(41)
其中,影响目标位置精度的因素有无人机位置Xuav,g以及无人机姿态ξ。显然,采用辅助姿态、滤波姿态、校正姿态进行目标位置求解,误差水平存在差异。
4 仿真验证
为验证方法有效性,进行仿真分析,分别在目标静止与目标运动两种条件下进行目标位置求解。
仿真流程如图2所示。其中,无人机与目标根据预定的航路与路径规划方案运动,在每个时间步长内,无人机根据IMU输出信息解算滤波姿态;判断无人机与目标、辅助信标的距离是否小于激光传感器的最大作用距离;首先进行无人机姿态解算,当可以观测辅助信标时,解算辅助姿态,得到辅助序列,并基于辅助姿态序列构建姿态偏差估计函数;当建立姿态偏差估计函数后,若能够观测目标,则根据目标位置观测值、无人机位置、校正姿态求解目标位置,对于运动目标,则进行跟踪,对于静止目标,则进行位置回归。为验证方法性能,分别通过校正姿态与滤波姿态求解目标位置,对比两种结果相对目标真实位置的距离偏差。
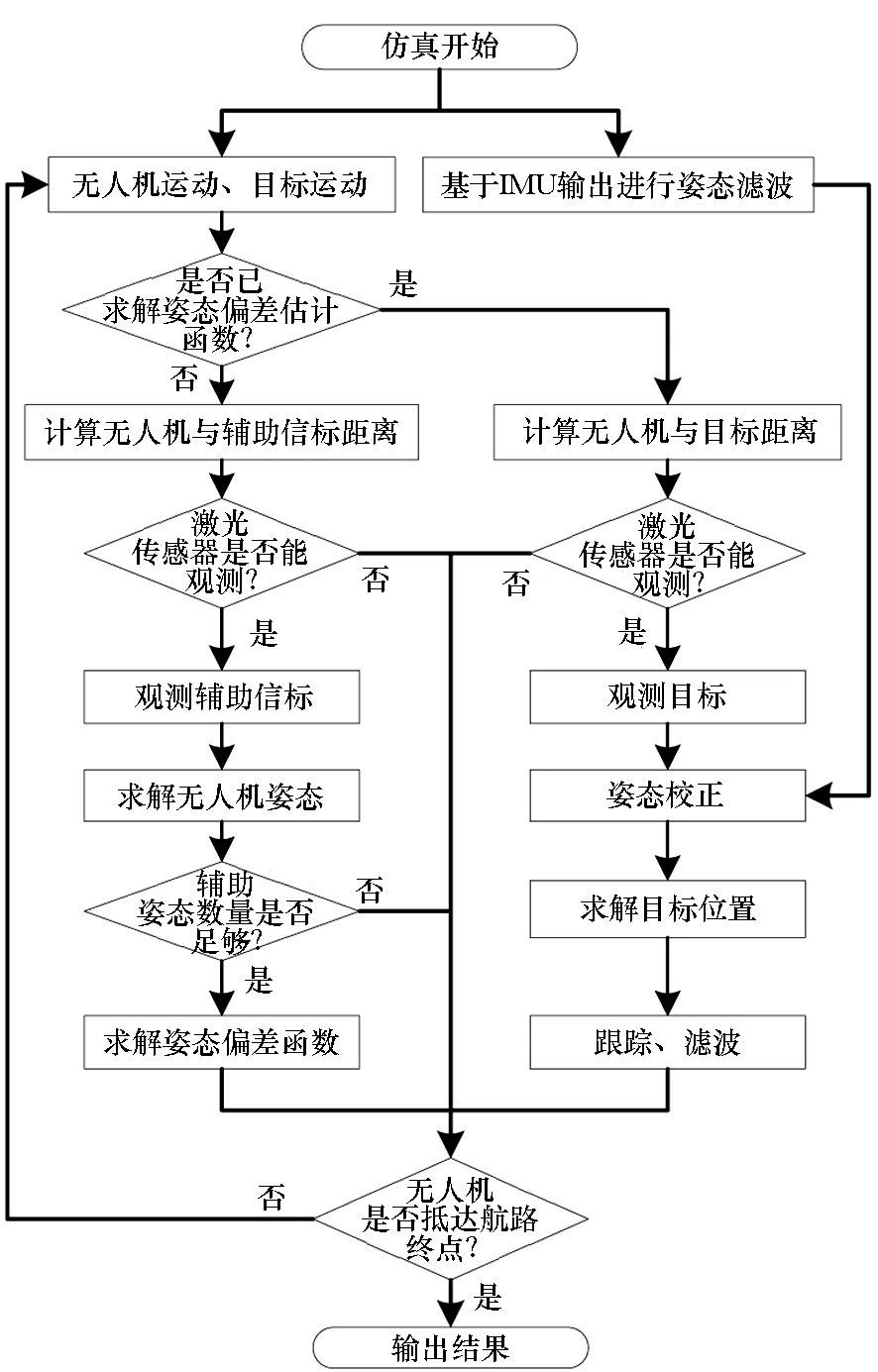
图2 仿真流程Fig.2 Simulation process
在仿真开始前,需要设定的初始条件包括:地形信息、航路信息、辅助信标位置、IMU漂移误差、IMU随机误差、激光传感器观测距离、激光传感器观测误差、无人机位置量测误差。
4.1 目标静止条件下的仿真分析
4.1.1 场景想定
仿真初值设定如下:航路起点坐标为(23 200 m,11 100 m,500 m);航路终点坐标为(1067 m,8100 m,500 m);辅助信标坐标为(10 130 m,5100 m,54.49 m);目标坐标为(4533 m,4300 m,8.75 m);无人机速度为40 m/s;无人机最小转弯半径为100 m;IMU输出漂移为(12°/h,8°/h,8°/h);IMU输出误差为(0.4°/s,0.3°/s,0.3°/s);激光传感器观测距离为10 000 m;激光传感器距离误差为80 m,水平角误差为0.057 3°,高低角误差为0.057 3°;无人机位置误差为(12 m,12 m,3 m)。
在目标静止的条件下进行仿真分析,场景想定如图3所示。其中,地形为沿海山地,选取地形中最高山峰作为辅助信标;无人机从航路起点飞行至航路终点,飞行过程中,首先通过观测辅助信标进行姿态偏差估计,之后根据校正姿态进行目标位置观测与求解。
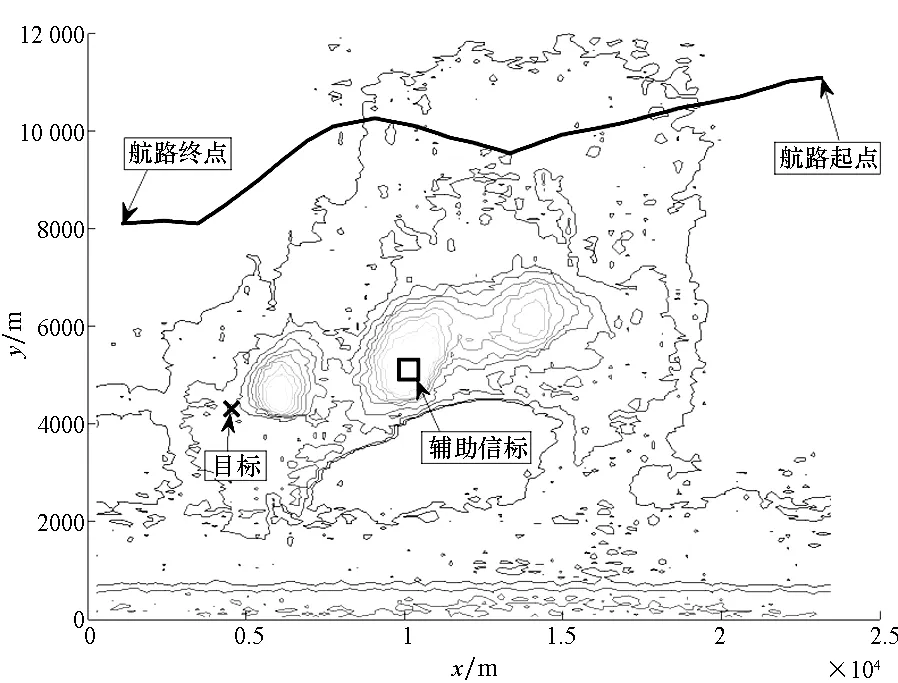
图3 场景想定一(静止目标)Fig.3 Scenario assumption No.1 (Stationary target)
4.1.2 仿真结果
分别采用一阶多项式与二阶多项式进行姿态偏差估计函数的构建。一阶多项式仿真计算结果如图4所示,二阶多项式仿真计算结果如图5所示。
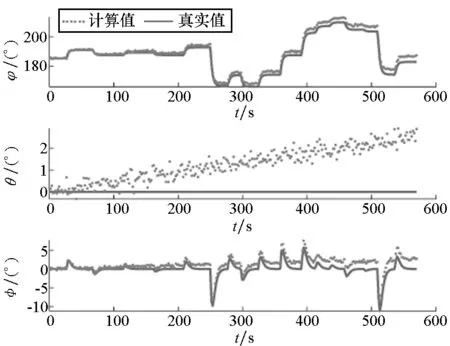
(a) IMU输出值与真实姿态(a) IMU output value and the true attitudes
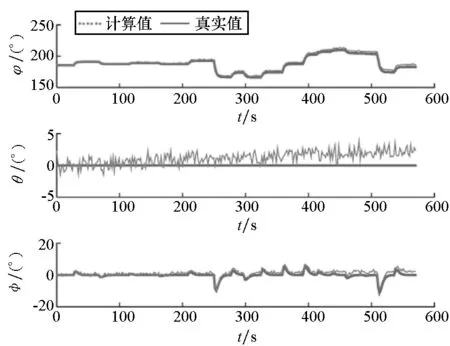
(b) 滤波姿态与真实姿态(b) Filter attitudes and true attitudes
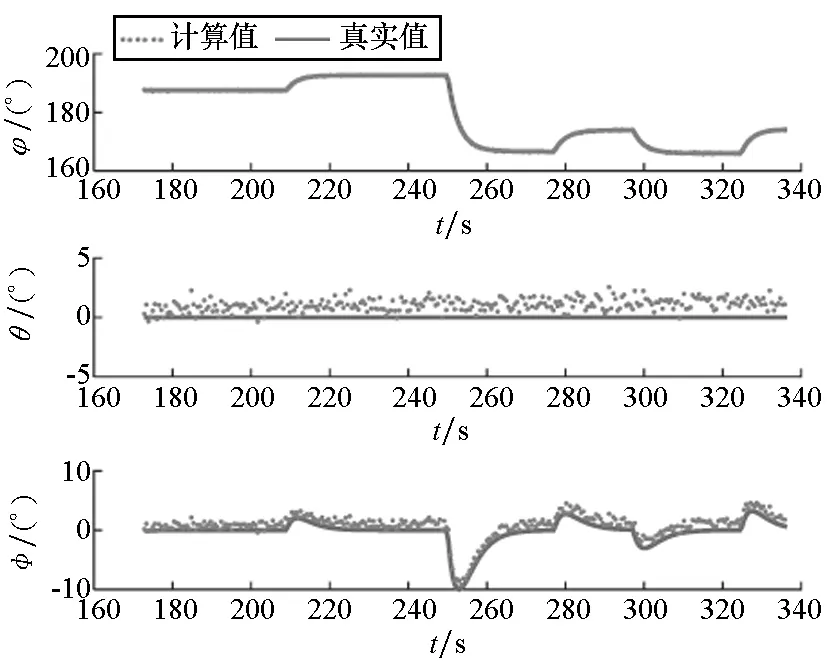
(c) 辅助姿态与真实姿态(c) Auxiliary attitudes and true attitudes
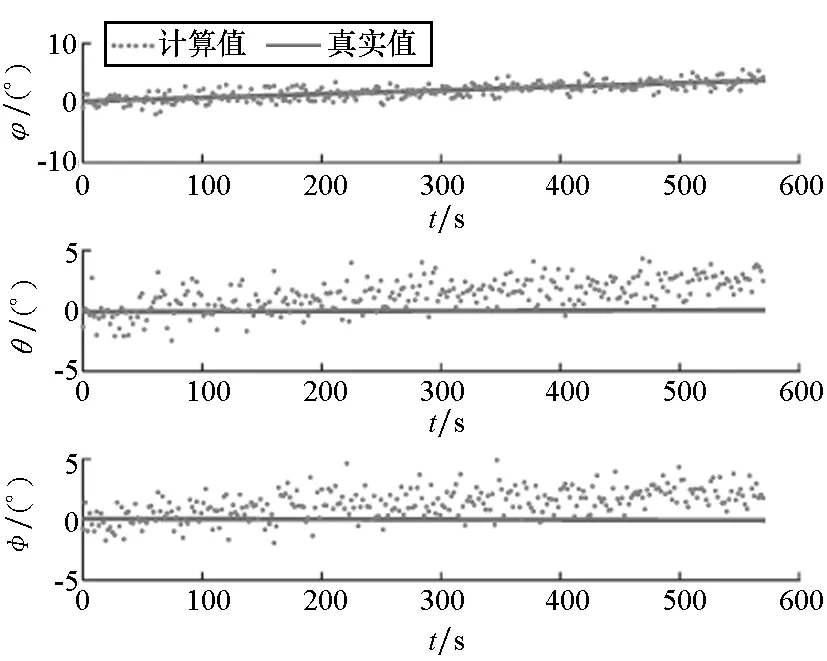
(d) 姿态偏差估计值与真实姿态偏差(d) Estimated value of attitude error and the true attitude error
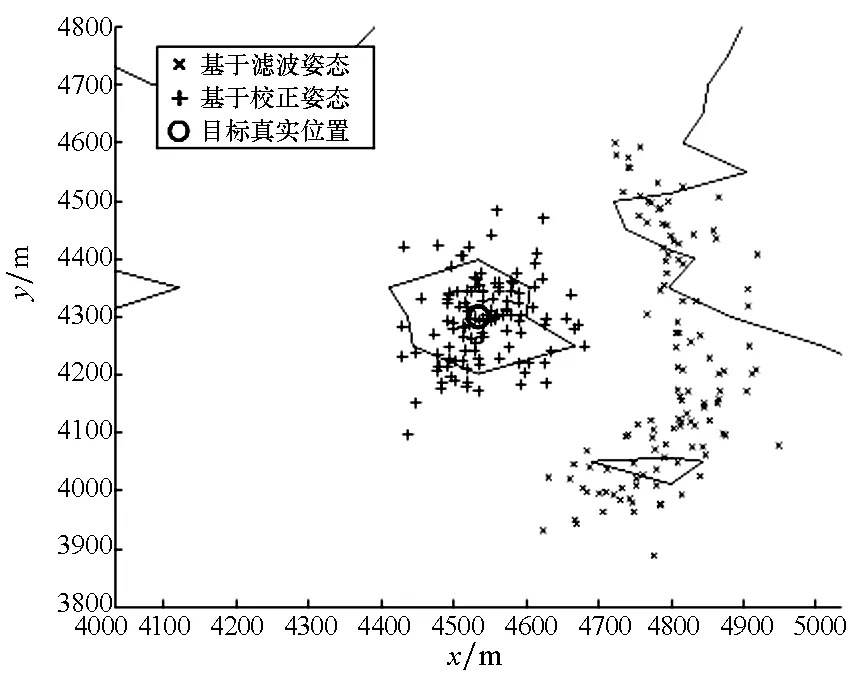
(e) 目标求解位置与真实位置(e) The solved targets′ position and the real position
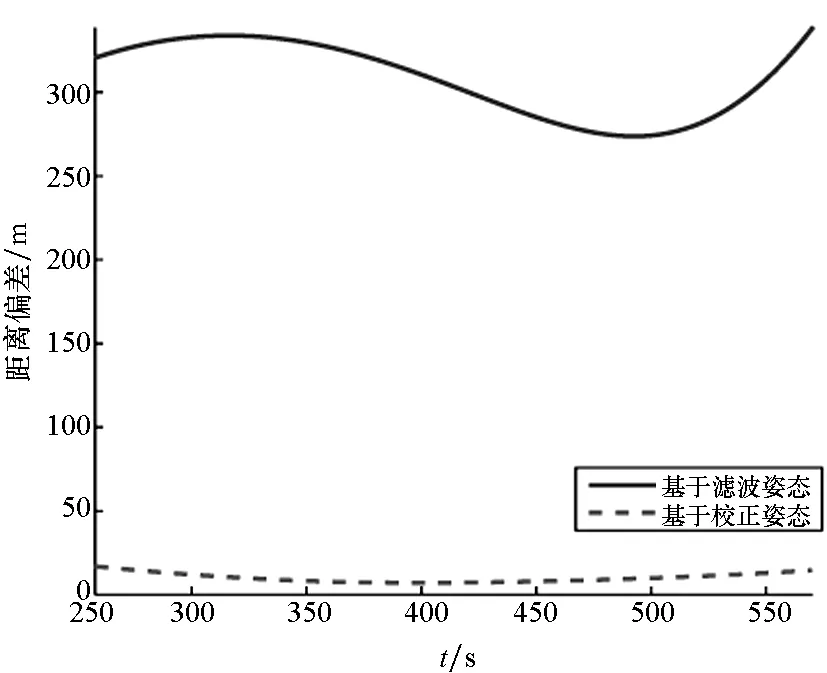
(f) 目标求解位置与真实位置的距离偏差(f) Distance deviation between solved targets′ position and the real position
图4 一阶多项式仿真计算结果
Fig.4 Simulation results of the first order polynomial
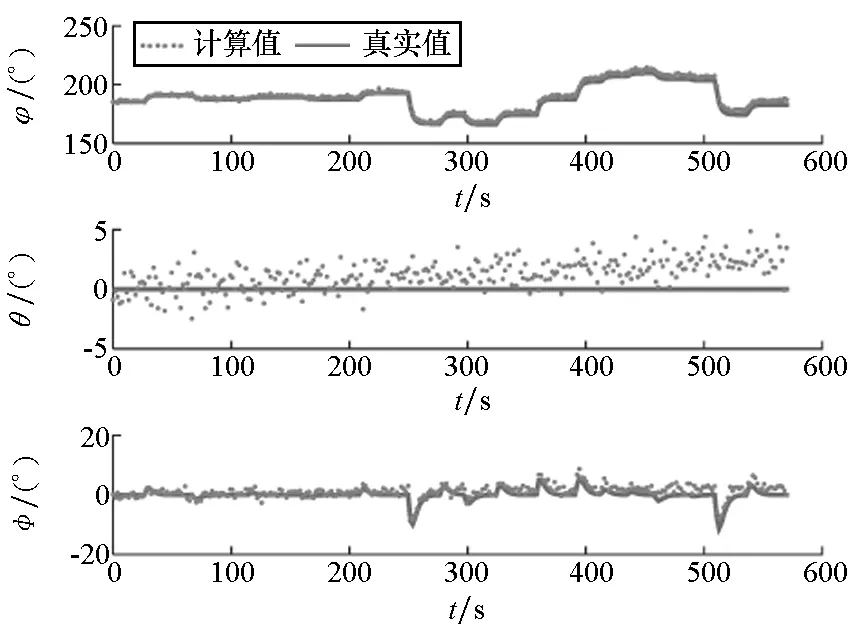
(a) IMU输出值与真实姿态(a) IMU output value and the true attitudes
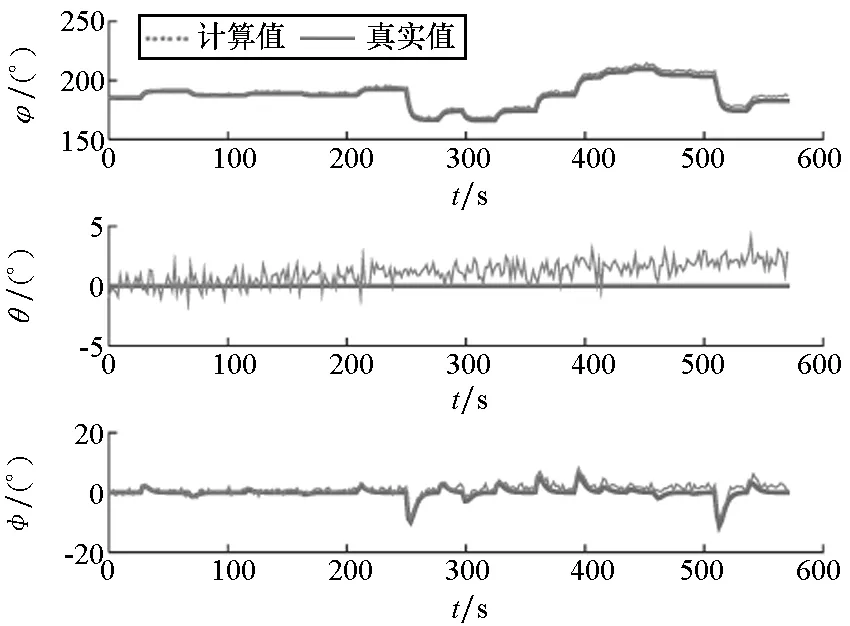
(b) 滤波姿态与真实姿态(b) Filter attitudes and true attitudes
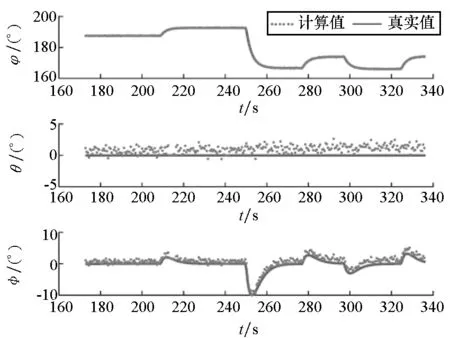
(c) 辅助姿态与真实姿态(c) Auxiliary attitudes and true attitudes
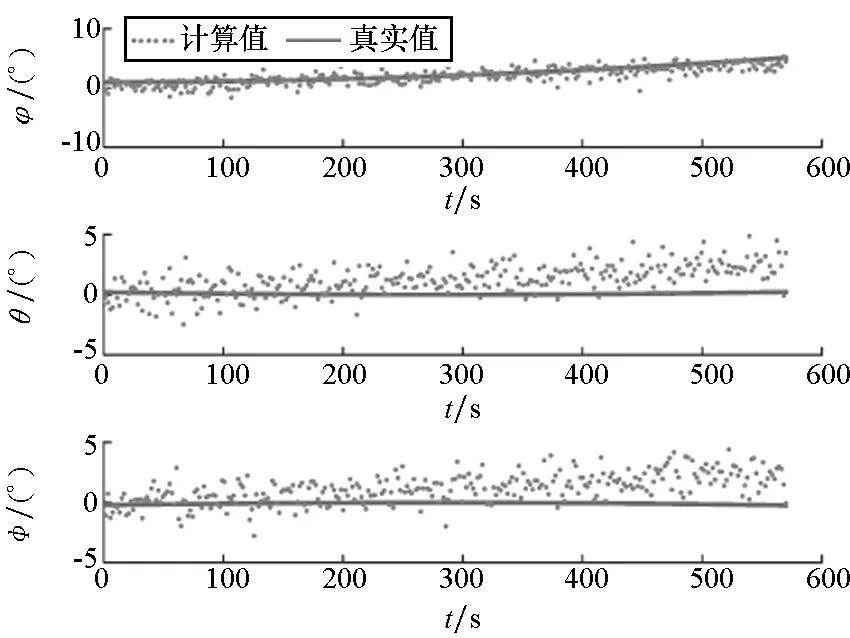
(d) 姿态偏差估计值与真实姿态偏差(d) Estimated value of attitude error and the true attitude error
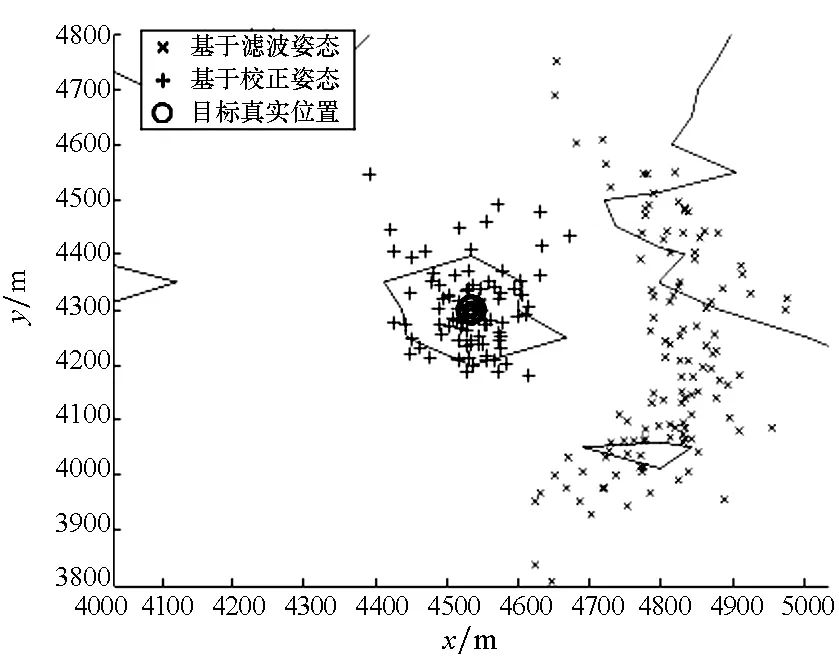
(e) 目标求解位置与真实位置(e) The solved targets′ position and the real position
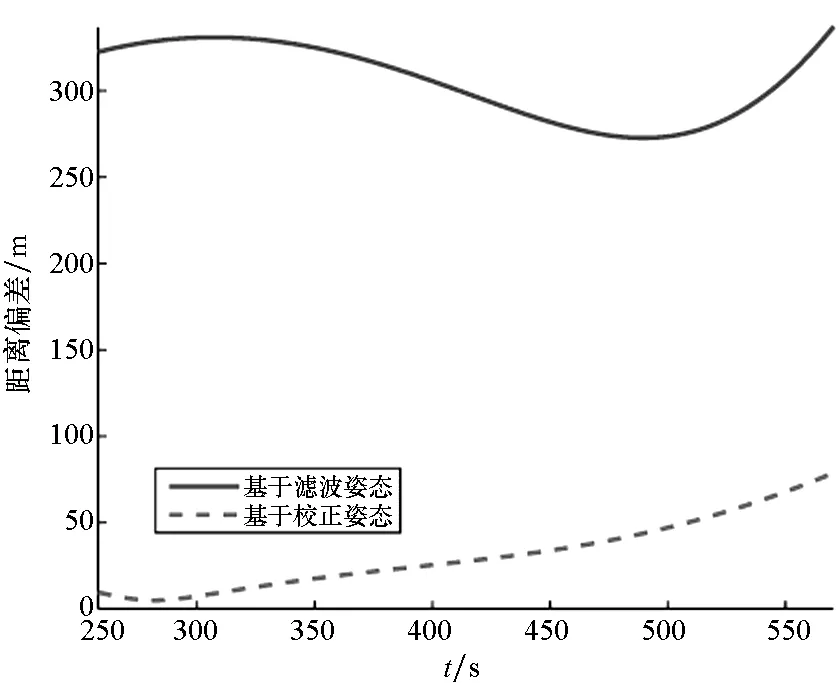
(f) 目标求解位置与真实位置的距离偏差(f) Distance deviation between solved targets′ position and the real position
图5 二阶多项式仿真计算结果
Fig.5 Simulation results of the second-order polynomial
4.2 目标运动条件下的仿真分析
4.2.1 场景想定
在目标运动的条件下进行仿真分析,场景想定如图6所示。其中,地形为沿海山地,选取地形中最高山峰作为辅助信标;目标从目标起点运动至目标终点;无人机从航路起点飞行至航路终点,飞行过程中,首先通过观测辅助信标进行姿态偏差估计,之后根据校正姿态进行目标位置观测与求解。
仿真初值设定如下:航路起点坐标为(23 200 m,11 100 m,500 m);航路终点坐标为(1067 m,8100 m,500 m);辅助信标坐标为(10 130 m,5100 m,54.49 m);目标坐标为(4533 m,4300 m,8.75 m);无人机速度为40 m/s;无人机最小转弯半径为100 m;IMU输出漂移为(12°/h,8°/h,8°/h);IMU输出误差为(1°/s,1.2°/s,1.2°/s);激光传感器观测距离为10 000 m;激光传感器距离误差为80 m,水平角误差为0.057 3°,高低角误差为0.057 3°;无人机位置误差为(12 m,12 m,3 m)。
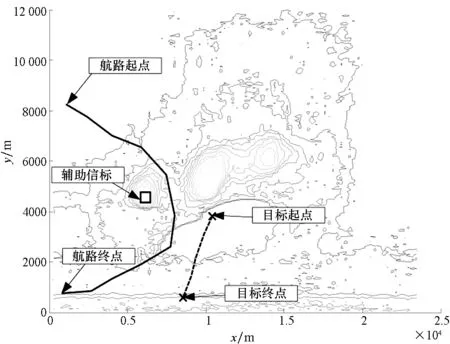
图6 场景想定二(运动目标)Fig.6 Scenario assumption No.2 (moving target)
4.2.2 仿真结果
分别采用一阶多项式与二阶多项式进行姿态偏差估计函数的构建。一阶多项式仿真计算结果如图7所示,二阶多项式仿真计算结果如图8所示。
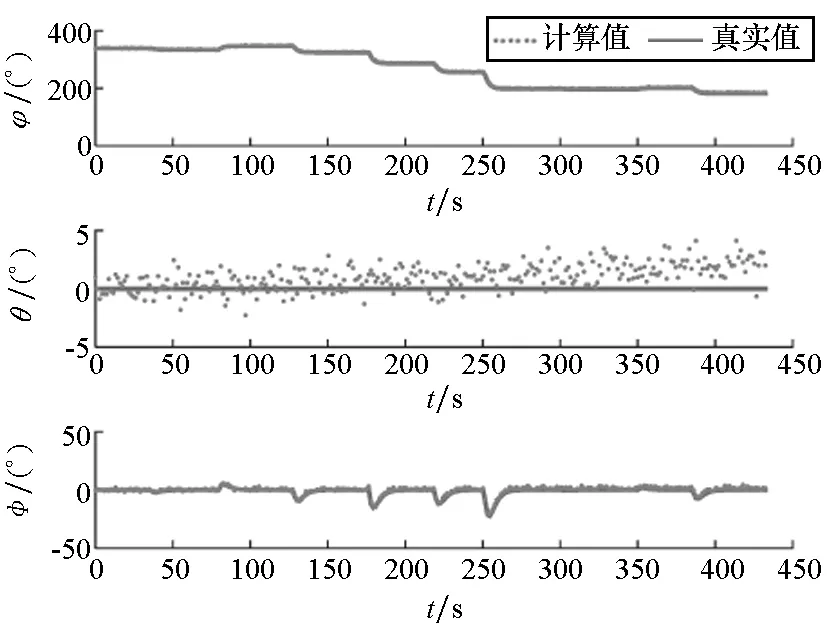
(a) IMU输出值与真实姿态(a) IMU output value and the true attitudes
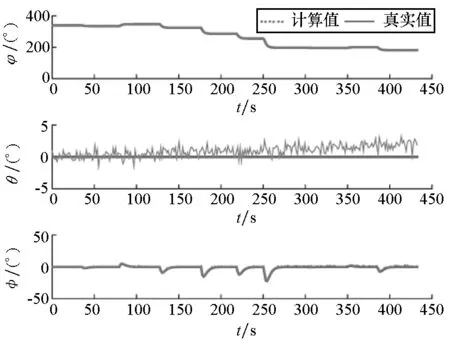
(b) 滤波姿态与真实姿态(b) Filter attitudes and true attitudes
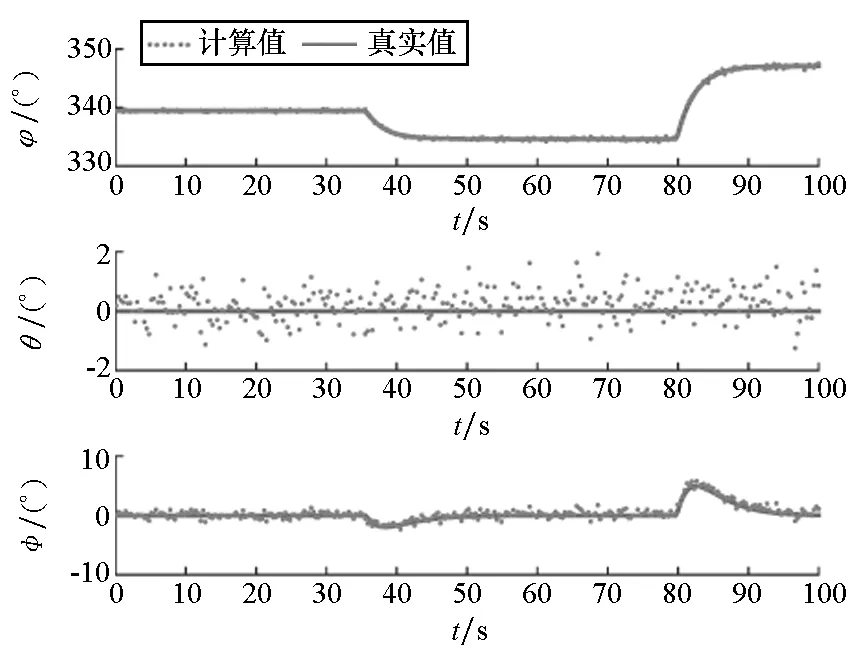
(c) 辅助姿态与真实姿态(c) Auxiliary attitudes and true attitudes
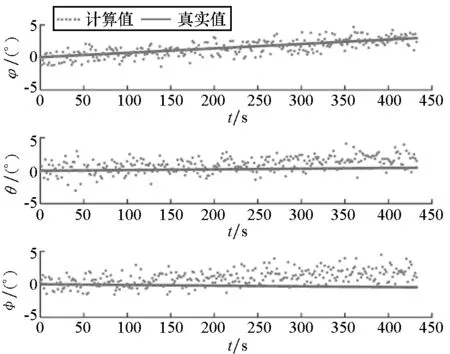
(d) 姿态偏差估计值与真实姿态偏差(d) Estimated value of attitude error and the true attitude error
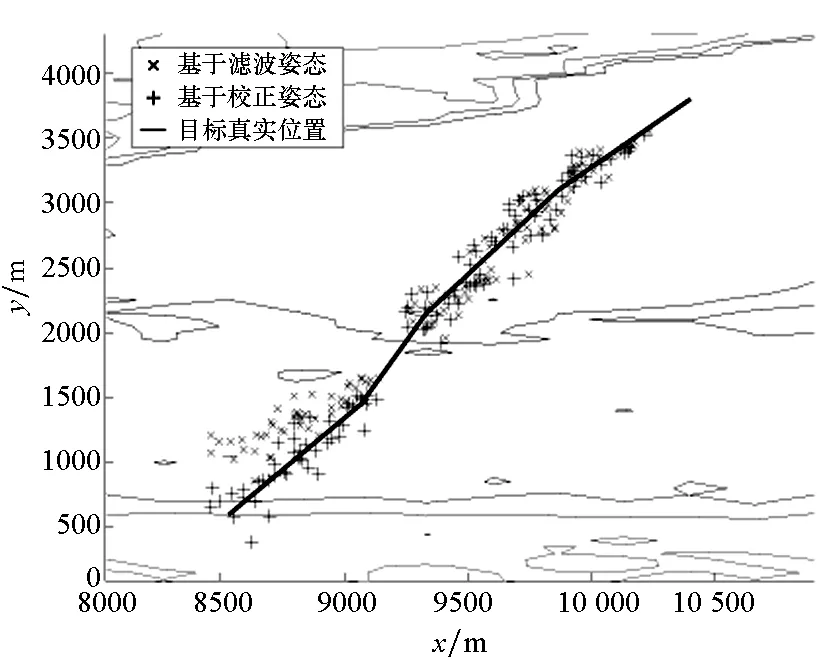
(e) 目标求解路径与真实路径(e) The solved targets′ path and the real path
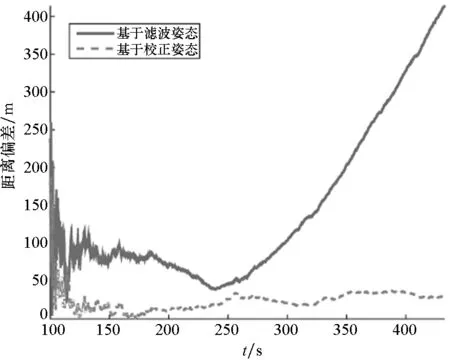
(f) 目标求解路径与真实路径的距离偏差(f) Distance deviation between the solved targets′ path and the real path
图7 一阶多项式仿真计算结果
Fig7 Simulation results of the first order polynomial
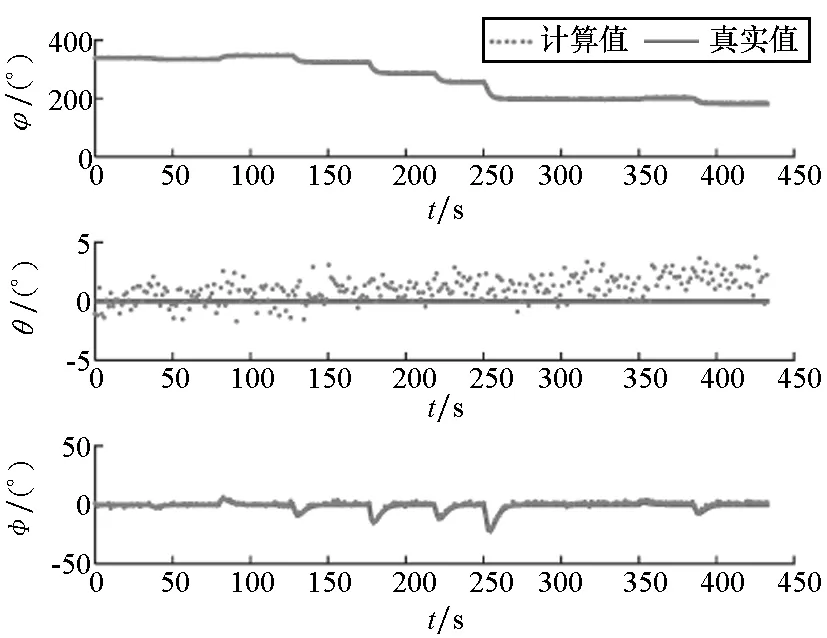
(a) IMU输出值与真实姿态(a) IMU output value and the true attitudes
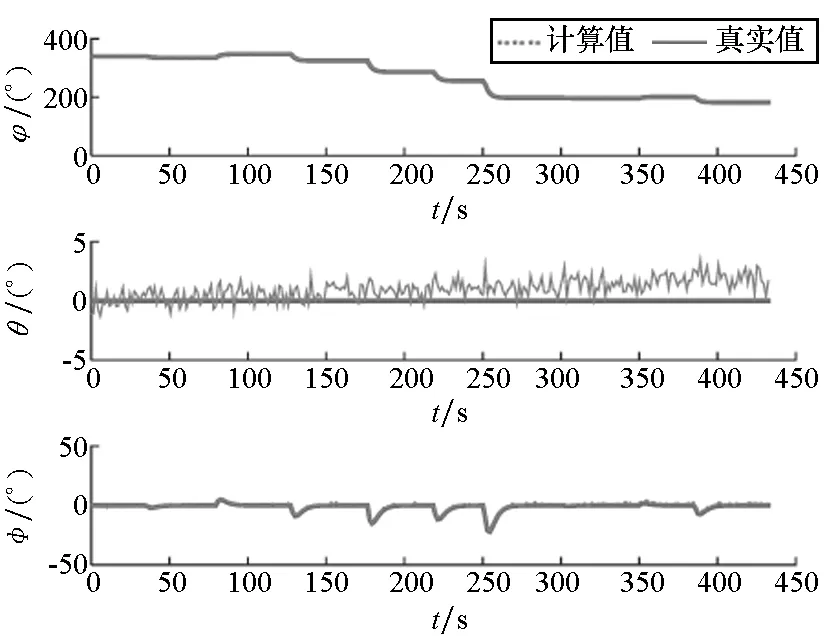
(b) 滤波姿态与真实姿态(b) Filter attitudes and true attitudes
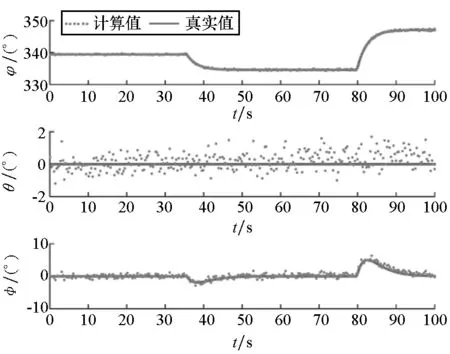
(c) 辅助姿态与真实姿态(c) Auxiliary attitudes and true attitudes
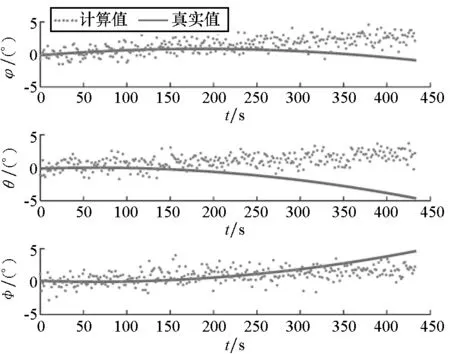
(d) 姿态偏差估计值与真实姿态偏差(d) Estimated value of attitude error and the true attitude error
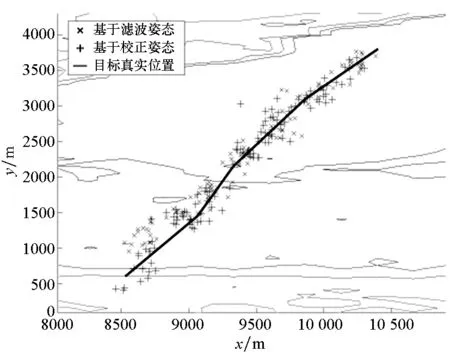
(e) 目标求解路径与真实路径(e) The solved targets′ path and the real path
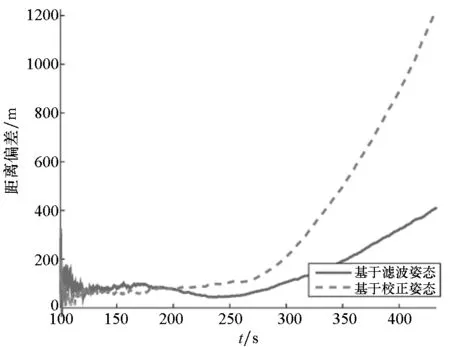
(f) 目标求解路径与真实路径的距离偏差(f) Distance deviation between the solved targets′ path and the real path
图8 二阶多项式仿真计算结果
Fig.8 Simulation results of the second-order polynomial
4.3 多辅助信标分段校正条件下的仿真分析
采用二阶多项式进行姿态偏差估计函数的构建,分别通过多辅助信标分段校正与单辅助信标一次校正的方法求解目标位置。
4.3.1 场景想定
在目标运动的条件下进行仿真分析,场景想定如图9所示。
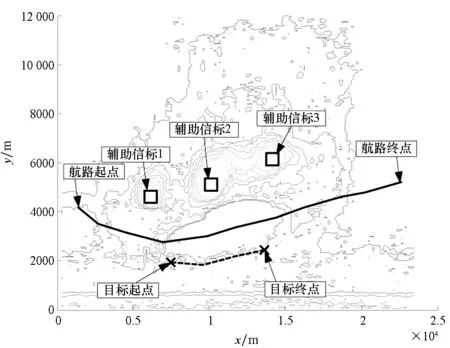
图9 场景想定三(多辅助信标分段校正)Fig.9 Scenario assumption No.3 (sectional correction based on multi-auxiliary beacons)
4.3.2 仿真结果
单辅助信标目标定位仿真计算结果如图10所示。
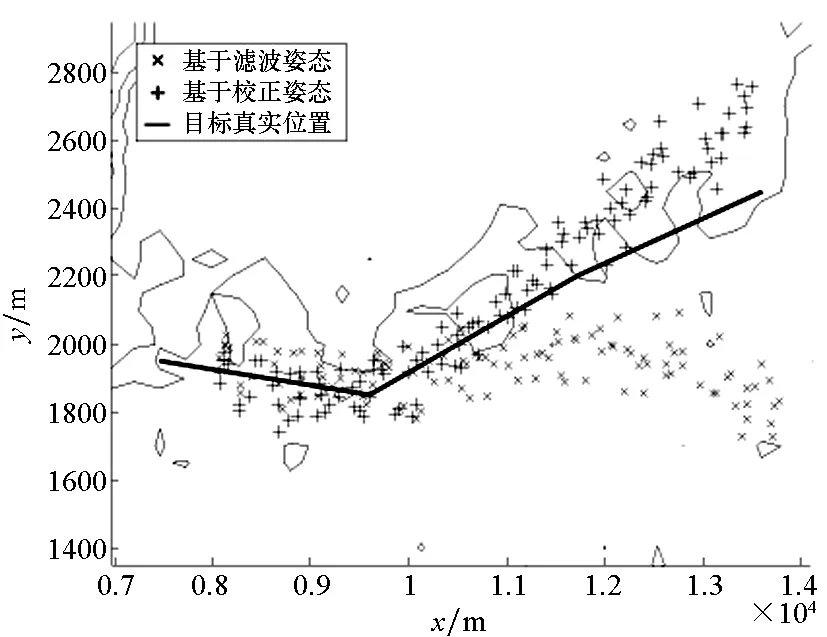
(a) 目标求解路径与真实路径(a) The solved targets′ path and the real path
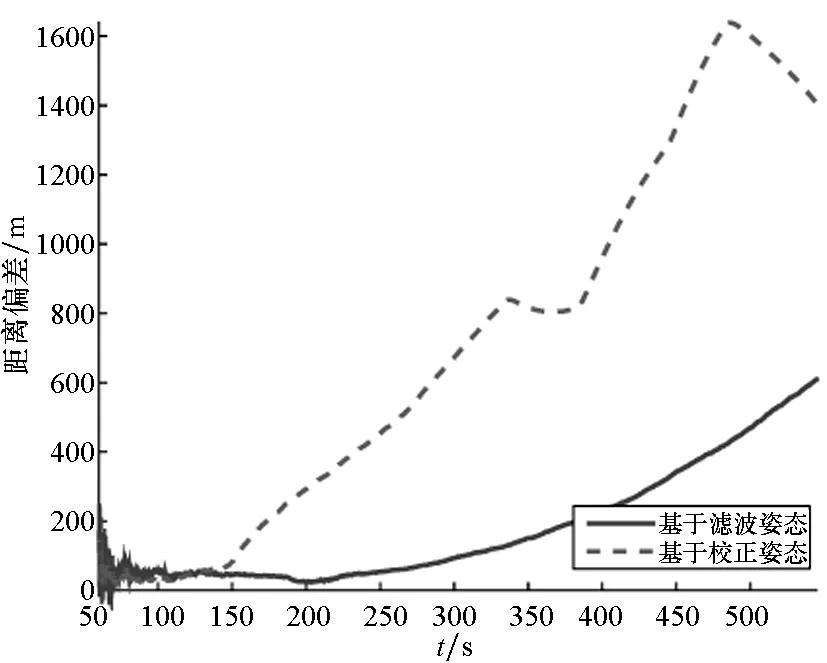
(b) 目标求解路径与真实路径的距离偏差(b) Distance deviation between the solved targets′ path and the real path图10 单辅助信标目标定位仿真Fig.10 Simulation of target location based on single auxiliary beacon
多辅助信标目标定位仿真计算结果如图11所示。
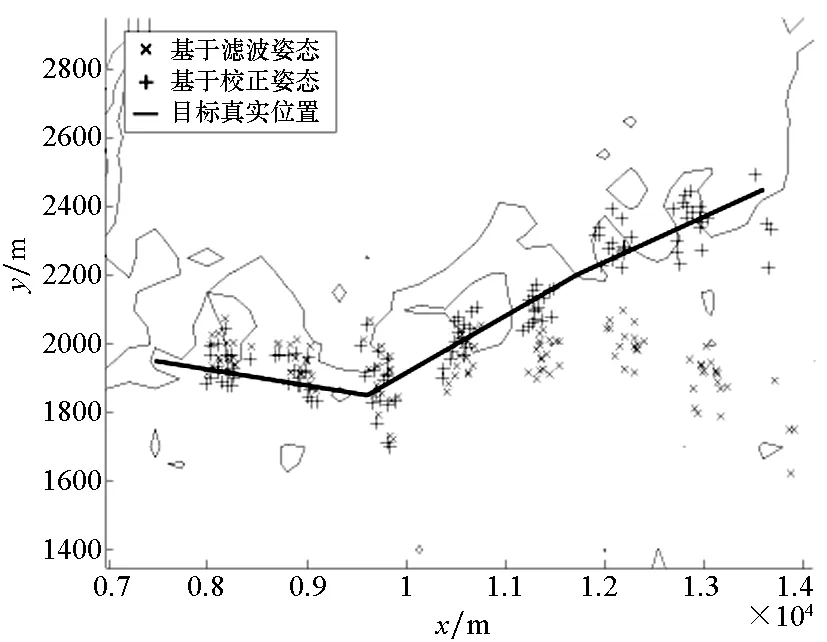
(a) 目标求解路径与真实路径(a) The solved targets′ path and the real path
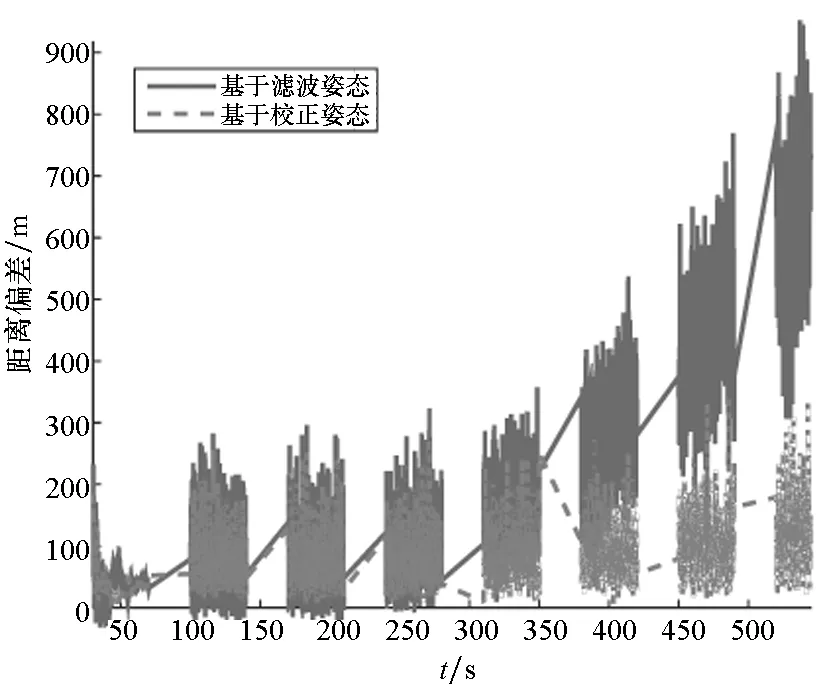
(b) 目标求解路径与真实路径的距离偏差(b) Distance deviation between the solved targets′ path and the real path图11 多辅助信标目标定位仿真Fig.11 Simulation of target location based on multi-auxiliary beacon
针对静止目标与运动目标,多次仿真并计算目标位置与真实位置距离偏差的平均值,作为衡量方法性能的指标。分别采用4.1.1与4.2.1中的仿真初始条件进行500次仿真计算,得到结果如表1所示。
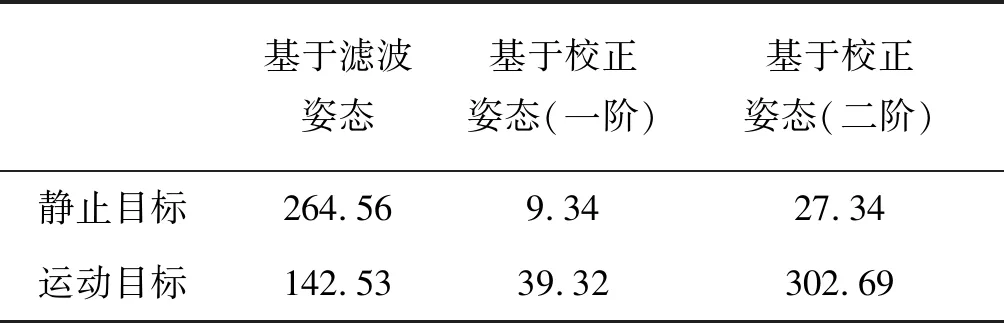
表1 目标位置求解误差
同时,分别采用多辅助信标多次校正与单辅助信标单次校正的方法求解目标位置,并与目标真实位置对比,求解距离差值的均值,500次仿真计算结果如表2所示。

表2 多辅助信标分段校正与单辅助信标求解误差对比Tab.2 The solved error comparison between multi-auxiliary beacon piecewise correction and single auxiliary beacon m
5 结论
根据仿真结果,可以得到如下结论:
1)基于辅助信标求解无人机姿态,进而构建姿态偏差估计函数,对跟踪目标过程中的滤波姿态进行修正,能够明显提高目标位置求解精度;
2)姿态偏差估计的精度与姿态偏差估计函数的选取有关,符合实际IMU漂移的函数对于偏差估计的精度至关重要,如果姿态偏差估计函数选取失当,反而会加大跟踪误差;
3)采用姿态偏差估计函数进行滤波姿态的校正时,若单次连续跟踪目标时间过长,可能导致姿态偏差估计函数的误差增加,进而影响跟踪精度。
综上,为进一步提高方法的适用性与准确性,还需要针对无人机实际搭载的IMU进行多次实验,总结IMU漂移规律,选取合适的姿态偏差估计函数;同时,在可能的情况下设立多个信标或多次观测辅助信标校正姿态,避免一次连续跟踪目标时间过长以致姿态偏差误差较大。
