北斗RDSS系统新体制信号子载波间干扰产生机理与消除方法

王 雷，陈华明，唐小妹，李井源，王飞雪

(国防科技大学 电子科学学院， 湖南 长沙 410073)

在新体制无线电测定卫星服务(Radio Determination Satellite Service， RDSS)信号中，采用了多个子载波信号调制的方式。在通常的导航信号接收中，当接收信号与本地信号存在频偏时，频偏会导致相干积分产生严重损耗，当频偏频率与相干积分时间的乘积接近甚至超过1时[1-2]，相关峰将产生严重损耗，信号将无法被检测到，因此对于信号频偏较大的情况，通常认为不会产生干扰。但在RDSS信号中，在所有子载波采用相同的同步头序列的情况下，其他子载波上的信号对在观测子载波上形成较大相关峰，对信号接收产生较大干扰。

1 RDSS新体制信号模型

RDSS信号为短突发信号，主要提供测距以及短消息服务[3]，RDSS新体制信号设计为提高有限带宽内信息服务能力，采用了多个子载波信号调制的方式，单个子载波采用二进制相移键控(Binary Phase Shift Keying, BPSK)调制方式，基带信号具体表达式为：

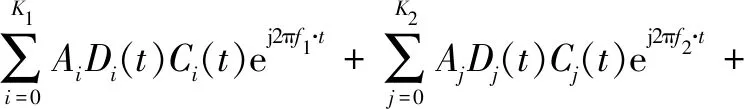
(1)

其中：f1、f2、f3分别为-4.08 MHz、0 MHz、4.08 MHz，即三个子载波的频率，后续三个子载波用子载波1、子载波2、子载波3指代，分别对应频率f1、f2、f3；A为信号幅度；D为信号电文；C为伪码，码率为4.08 MHz；K1、K2、K3为子载波上信号数量，由于RDSS具有短突发信号特性，因此K1、K2、K3并非固定值。

信号的功率谱如图1所示。

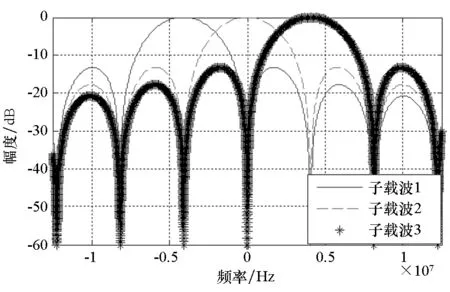
图1 RDSS信号功率谱Fig.1 Power spectral density of RDSS signal

如图1所示，三路子载波之间的中心频率间隔为4.08 MHz。

由于RDSS信号均为短突发信号，为便于信号检测，所有信号开始均有一段相同的同步头，通过检测同步头检测信号是否存在并确定信号的起始位置。其时域图如图2所示。

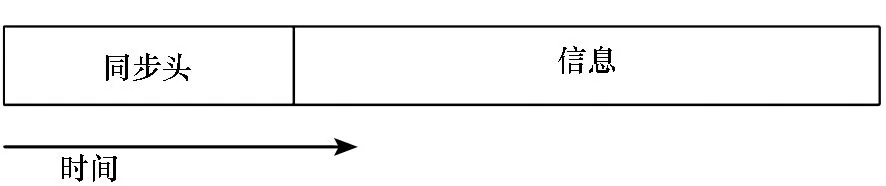
图2 RDSS信号时域Fig.2 Time domain of RDSS signal

在初始设计中，子载波1和子载波2为民用信号频谱，采用相同的同步头设计。

2 信号干扰分析

针对RDSS单个信号的检测是利用本地信号与接收信号进行相关累积运算，将累积结果与门限进行比较，超过门限则认为信号存在并可确定信号的起始位置。

传统的分析过程中针对多用户信号仅作为多址干扰进行分析，而在相关域则将频率偏移损耗和相关损耗分别加以分析。

2.1 多址干扰分析

在以往的分析中，通常认为除观测信号以外的其他信号所产生的影响为多址干扰，并将多址干扰对当前观测信号的主要影响归因于等效载噪比的损耗[4]。多址干扰下系统载噪比为[5]：

(2)

其中：

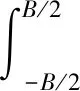
(3)

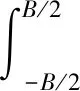
(4)

其中，B为接收机前端滤波器双边带宽，η为经过带限滤波器的信号功率百分比，Gs(f)、Gi(f)分别为信号和多址干扰信号的归一化功率谱，Cs为信号功率，CI为多址干扰功率，N0为噪声功率谱密度。

2.2 相关域分析

接收信号首先根据观测子载波频率将信号下变频到基带，下变频后表达式为：

s(t)=Ac(t)ej(2πfbias·t+θe)

(5)

其中：A为幅度；c(t)代表伪码；fbias表示接收信号下变频后的频率残余，接收信号子载波频率与观测子载波非同一个子载波时，fbias包含了两个子载波频率之差以及信号多普勒；θe为信号的初始载波相位。

利用本地基带信号与接收信号进行相关累积，在以往的分析中，通常将伪码相位未对齐造成的损耗和载波频偏造成的损耗分别予以处理，文献[1]推导了在存在载波频偏的情况下相关累积与载波频偏的关系：

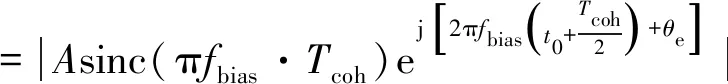
=A|sinc(πfbias·Tcoh)|

(6)

其中，d代表相关累积值，‖代表取模，t0表示相关累积初始时刻，Tcoh为相关累积时长。

在上述分析的结果中，相关累积值随频偏与相干积分时间的乘积成sinc函数衰减。根据sinc函数特性，当fbias·Tcoh>1时，相关累积值将产生较大的衰减，无法正常捕获跟踪信号。

根据上述分析结果，在RDSS系统中，设定相关累积时长Tcoh为1 ms，子载波之间的频偏fbias取值为±4.08 MHz、±8.16 MHz，载波频偏与相关累积时长的乘积fbias·Tcoh≫1，频率偏移造成的损耗足够大，相关结果将很小。多址干扰在信号路数较少时影响也很小。但是RDSS在信号接收中并非如此，例如-4.08 MHz子载波上的信号，在0 MHz子载波上进行捕获会产生相关峰，如图3所示。在频率间隔8.16 MHz的子载波上同样会产生相关峰。

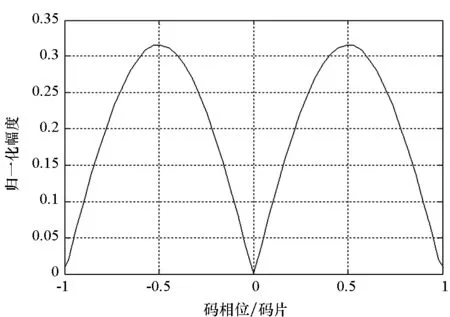
图3 跨子载波相关峰Fig.3 Correlation peak across subcarriers

上述问题在以往的分析中均没有针对多址干扰和相关域载波频偏的分析，本文将据此展开研究。

3 相关峰理论分析

针对频率偏移为整数倍子载波频率偏差的情况，对单个信号相关峰进行理论分析。

首先设定频率偏移满足如下关系：

(7)

其中，Tchip为码片时间宽度，fsub为子载波之间的频率间隔，由于正频率和负频率具有对称性，因此l取值仅考虑正值。

在上述条件下推导相关值的理论表达式，在相关累积过程中，伪码码片对齐的部分，能量将会得到积累，伪码码片没有对齐的部分，对应着伪码互相关，相比于自相关的能量小很多，本文将该部分忽略，产生的影响很小[6-8]。

以N表示相关累积时间内的码片数量，推导过程中应用了如下关系：

Tcoh=NTchip

(8)

可得相关累积结果如下所示：

(9)

根据上述推导可知，相关峰的顶点对应的码相位满足如下关系：

fbias·τ=2s+1s=0,1,…

(10)

与式(6)结合可知，在无多普勒的情况下，相关峰损耗满足如下关系：

(11)

由式(10)、式(11)可得到相关峰值与载波频偏的关系，如表1所示。

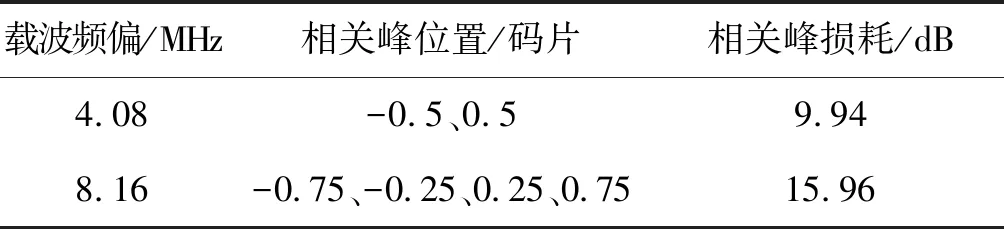
表1 相关峰值与载波频偏关系

将理论推导结果与仿真结果进行对比，仿真数据的采样率为100 MHz，两者对比结果如图4～5所示。

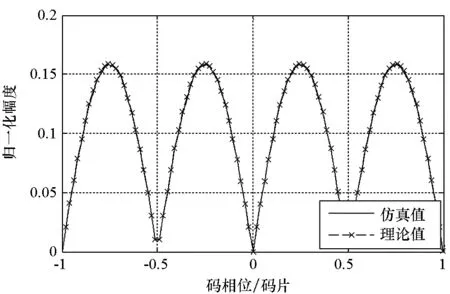
图5 8.16 MHz频偏理论相关值与仿真结果对比Fig.5 Comparison of the theoretical correlation result withthe simulation result under 8.16 MHz frequency bias

由图4～5可知，理论分析结果与仿真结果基本吻合，证明了理论推导的正确性。由此可以得到下述结论：

1)从理论推导的过程可知，在上述条件下产生相关峰是由于伪码码率与载波频偏频率呈倍数关系，积分过程中伪码相关和载波能量积累无法隔离，导致单载波功率得到了累积。

2)在上述条件下，相关峰形状并非伪码相关的三角形，由于单载波的周期性，会存在多个相关峰。相比于伪码相关的三角形相关峰，上述条件下的相关函数具有以下几个特点：一是具有多个相关峰；二是相关峰顶点存在偏差，并非码相位为零的位置，而是满足式(10)的位置，畸变的相关函数导致最终测量得到的伪距值产生偏差[9-10]；三是相关峰峰值存在损耗，损耗大小满足式(11)，具体数值见表1。

因此，上述相关峰会对信号接收产生较大干扰，容易造成信号的错误锁定，错误锁定信号具有较大衰减，容易造成较大的误码率，而且相关峰具有较大的码相位偏差，从而产生测距偏差。在实际应用中，应消除相关干扰的影响。

4 相关干扰消除方法

通过上述分析可知，相关干扰问题产生的必要因素有两个：一是两个子载波上的伪码序列相同；二是载波频偏为伪码速率的整数倍。因此，针对上述问题主要考虑相关干扰的消除方法，即采用不同的伪码序列和增加频率隔离。

1)不同的子载波采用不同的伪码序列，子载波之间互相关性将会降低，式(9)中能量不能得到累积，可以解决该问题，但是信号发送和接收需要切换伪码序列，在一定程度上增加了设计复杂度。

2)增加频率隔离，使得子载波频率偏移码率为整数倍，该方案对应的发射频率和接收频率需要进行修改，但是发送和接收过程增加的复杂度较小。

进一步针对载波偏移对相关累积的影响进行分析。假设接收信号频率偏移在伪码码率整数倍基础上进一步叠加频率偏移，用fb表示，则此时相关累积值表达式如下所示：

d′=d|sinc(fb·Tcoh)|

(12)

其中，d对应式(9)中的结果。将理论分析结果与仿真结果进行对比，图6所示为相干积分长度为1 ms的情况下相关峰峰值与多普勒频率的关系。

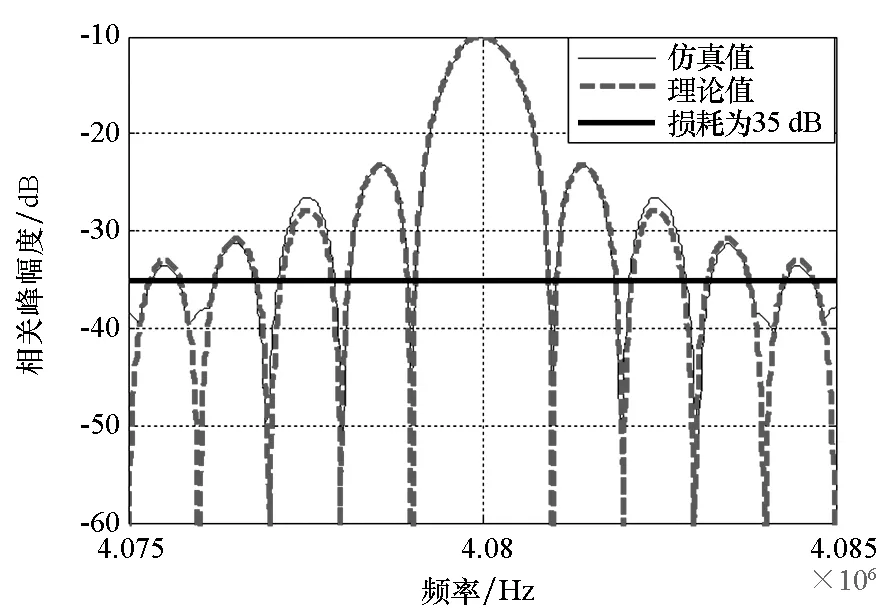
图6 载波频偏相关损耗理论值与仿真值对比Fig.6 Comparison of correlation loss versus frequency bias between theoretical result and simulation

由图6可知，相关峰峰值随多普勒理论分析结果与仿真结果基本一致，在多普勒变大的时候吻合度降低，但是差距较小，上述表达式基本可以反映叠加频率隔离的情况。

图6中相关干扰影响可以忽略，在相干积分时间为1 ms的情况下，频偏约为4.8 kHz以上可以保证满足该要求。

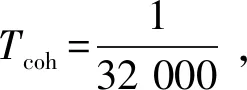
进一步对RDSS信号主要带宽范围内的相关峰进行分析，以1 kHz为间隔，图7反映了本地信号与接收信号相关峰峰值与载波频率偏移的关系。

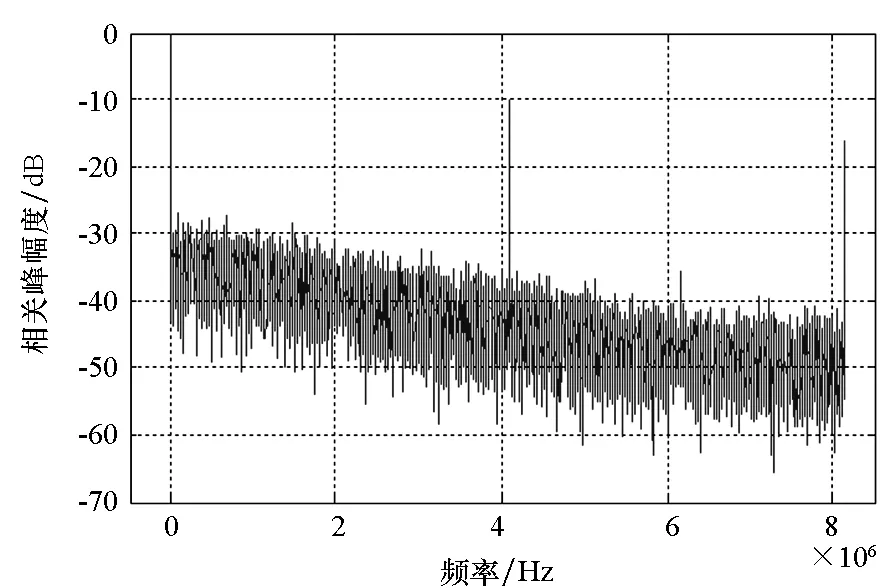
图7 频谱范围内相关峰与频率的关系Fig.7 Correlation peak versus frequency in receiving bandwidth

由图7可知，在RDSS信号主要带宽范围内，随着接收信号与本地信号频偏增大，相关峰峰值呈下降趋势；在4.08 MHz和8.16 MHz的位置上存在较大的相关峰峰值，在其他频率点基本没有较大的相关峰存在。

因此，理论分析增加子载波频偏200 kHz以上解决子载波间相关干扰的方法，完全可以满足要求。

5 结论

本文分析了RDSS新体制信号中其他子载波信号在观测子载波上形成相关干扰的问题，给出了该相关峰的具体理论表达式。这一现象会造成信号错误锁定，信号接收会存在较大伪距偏移以及载噪比损耗。根据理论分析以及仿真验证，本文提出了两种相关干扰消除方法，即不同子载波采用不同伪码序列和增加频率偏移两种方式，这两种方式均可有效解决相关干扰的问题，具备实际的工程应用价值。