黄土高原油松人工林土壤水分变动的人工神经网络模型研究

尹准生 唐孝甲 卢佶 洪奕丰 陈伟 左松源



黄土高原油松人工林土壤水分变动的人工神经网络模型研究

尹准生 唐孝甲 卢佶 洪奕丰 陈伟 左松源

（国家林业和草原局华东调查规划设计院 浙江杭州 310019）

依据黄土高原油松人工林试验样地林分情况，确定神经网络的输入变量和输出变量，利用2012—2015年的567组数据对网络模型进行训练和检验，构建了5∶q∶1的土壤水分变动的BP神经网络模型。结果表明：最适宜的网络结构为5∶6∶1，均方误差mse=0.002 645，总体拟合精度为96.78%，模拟检验拟合精度为94.44%。

土壤水分变动模型；人工神经网络；油松；黄土高原

作为陆地植被生态系统的主体，森林与其所生存的环境之间存在着巨大的相互作用[4,11]。黄土高原森林由于降雨量小但蒸发量大的干旱气候特点，森林与其生存环境间相互作用方式与此特点有着一定的相关性，具有特殊的水文效应[10, 15, 16, 18]。在目前大量的土壤蒸发模型中，虽然国内外学者进行了大量的研究工作，但在野外林地所做的研究则比较少，这是因为实际的土壤蒸发涉及到诸多的因素。林地土壤水分的变动不仅受到气象要素（如大气温度、湿度、风速、太阳总辐射等）、地形条件、土壤水分状况的影响，同时还受到林地小环境（林分郁闭度、枯落物、林下植被等）的影响。特别是，在野外的实际研究中还受到降雨等因子的影响，这些复杂的因素都限制了土壤蒸发模型的研究。

人工神经网络（artificial neural network）是一种应用类似于大脑神经突触联接的结构进行信息处理的数学模型。人工神经网络具有全局并行、局部处理和非线性三大特点，信息处理能力很强。由于神经网络对于非线性系统建模具有很强的拟合性，利用神经网络的非线性特质，可用于解决许多比较复杂的非线性问题[1-3, 5-8]。本文以黄土高原油松（）人工林为研究对象，根据测试区的实际情况选取相关变量建立神经网络模型，并以实测数据对网络模型进行训练、模拟和评价，探索林地土壤水分变动量与相关因子之间的关系，从而为森林水文的研究和生态环境建设提供理论参考。

1 数据来源

研究地点位于山西省偏关县陈家营乡，地处晋西北的晋蒙交界处，东经111°22′～11°01′、北纬39°12′～39°40′，为大陆性气候，年平均气温4.3 ℃，年平均降雨量为425.3 mm，7-9月份的降雨占全年的60%以上，植被以人工乔木林和灌木为主，造林树种主要为油松、落叶松、樟子松，土壤为沙质黄绵土。供观测的人工油松纯林为28年生，平均树高4.3～5.2 m，平均胸径9.4～11.9 cm，郁闭度0.67～0.85。

本研究采用设置长期固定标准地的方式对林地内外气象因子进行定位观测，共设置了3个固定样地，各样地具体特征见表1。试验数据于2012年起进行观测。

表1 油松试验林基本情况

每个林内样地和气象站内各设置2个土壤蒸发器。土壤蒸发器由两部分组成，内筒所使用的材料为PVC管，内径25cm，高25cm；外筒采用镀锌板制作而成，其内径略大于内筒外径。在无降雨情况下，蒸发器的测量周期为3~5天，每次的测量时间为当日18时。考虑到降雨后土壤的水分变化较大，为了保证网络模型训练的质量，所以每次降雨后对其进行加测。林外气象站在每天的8：00、14：00和20：00进行水面蒸发、降雨量、温度、湿度、风速及光照的测定。表2为2012—2015年的调查数据汇总。

表2 2012—2015年调查数据汇总

2 研究方法

2.1 问题分析

在本研究中，针对土壤水分的研究主要是通过土壤蒸发器来进行，并且蒸发器土壤表面均覆盖接近于自然状态的枯枝落叶，以便能更好地反应林地的现实状况，通过一段时期两次土壤蒸发器重量之差来度量一定时间段内的土壤水分变动量。由赵鸿雁等给出的枯落物覆盖下土壤蒸发数学表达式可知，一段时间内的土壤蒸发量与原始土壤含水量和时间长短有关，同时也与枯落物厚度有关。但本研究中，根据实际情况和便于模型的建立，枯落物层的厚度被看作是恒定不变的。

土壤蒸发力的大小与气象因子的蒸发力及林分结构密切相关，气象因子涉及到如空气温度、空气相对湿度、风速、光照等，而这些因子所引起的土壤蒸发潜力可通过水面蒸发量得到衡量。而且水面蒸发量越大，其土壤蒸发潜力就越大。由于该地区的林分经人工抚育后林相整齐，林分的结构主要与郁闭度有关。基于此，并为了减少构造模型的复杂性，研究在气象因子方面只考虑一段时间内的水面蒸发量，而林分结构则只考虑郁闭度。

在实际的野外林地中，除了土壤蒸发损失水分之外，土壤本身还接受降雨的水分补给，因此降雨也会影响到土壤水分的变动。但在林地中，由于林冠、林下植被及枯落物的截留等作用，会影响到达土壤层的水分，所以在考虑土壤水分变动时也应将其考虑在内。

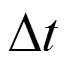
2.2 模型建立

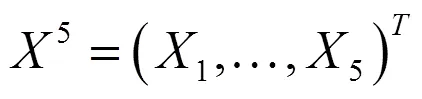
根据以上分析，先利用公式（1）进行网络隐含层神经元个数的初步训练，然后采用试错法确定其隐含层数，使其在满足一定的精度要求下取其最小值以提高网络的泛化能力[19]。

（1）

式中：为一整数，常在1到10之间取值。

网络的结构可表示为图1。

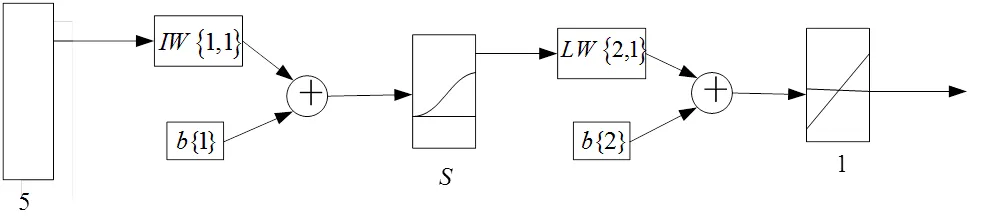
图1 BP神经网络结构

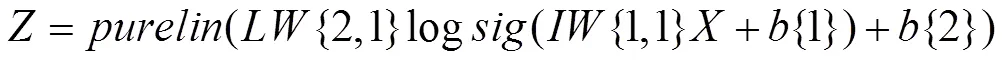
3 模型的训练与检验

3.1 模型的训练

（3）

式中：为原始数据；为转化后的数据；min和max分别为中的最小值和最大值。

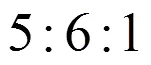
3.2 模型的模拟检验

选取2015年的144组数据用MATLAB的仿真函数sim进行仿真检验，并对其仿真的结果进行拟合精度分析，最后得出的拟合精度计算公式为：

（4）

式中：c表示拟合精度；表示理论值即网络的模拟值；表示真实值即实际调查值。

经计算可得拟合精度为94.44%，如图2所示，其结果表明BP神经网络模型的仿真理论值能够较好地跟踪实测值，结果令人满意。

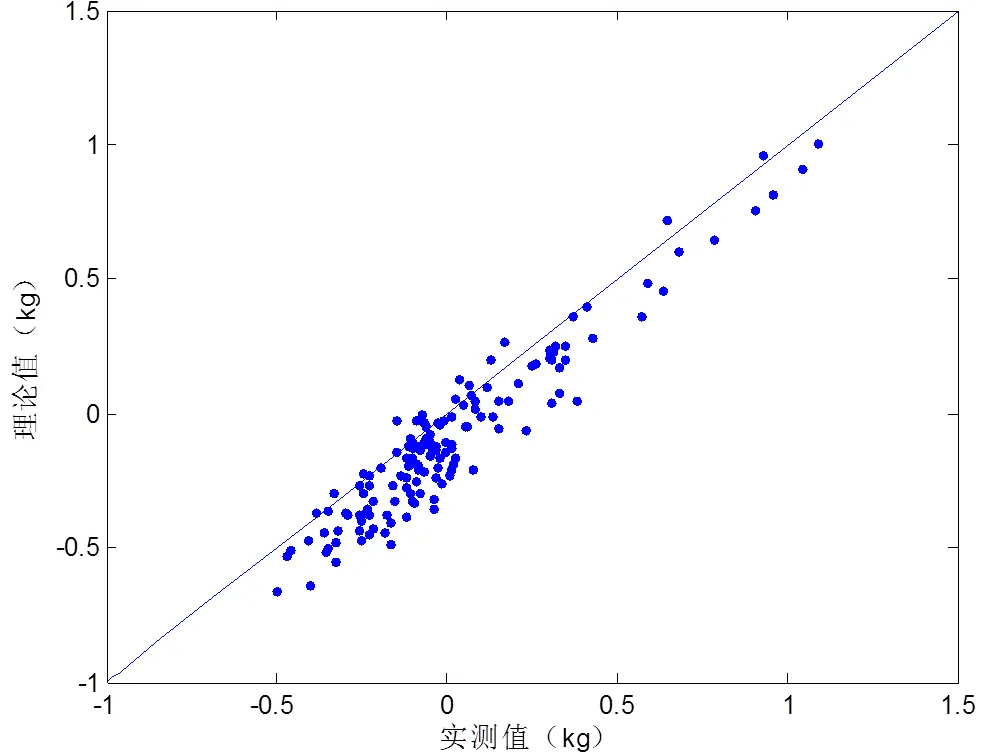
图2 网络模拟结果

4 结论与讨论

根据影响林地土壤水分的主要因素，建立土壤水分变动的BP神经网络模型。得出最适宜的网络结构为5:6:1，均方误差mse=0.002 645，总体拟合精度为96.78%，模拟检验拟合精度为94.44%，结果显示效果良好，表明将BP网络用于黄土高原林地土壤水分变动模型研究是可行的。但由于网络的训练过程是利用网络结构和参数来反映所研究的关系，网络中的参数没有具体的物理意义，不能反映出真实的物理过程，这是神经网络模型的主要局限。另外，由于试验地的区域性以及区域内的特殊性，模型有一定的适用范围，对于其他条件下如不同地区、不同树种、结构林分是否适用还有待今后进一步研究。

[1] Minns A,Hall M. Artificial neural networks as rainfall-runoff models. Hydrological Sciences Journal,1996, 41（3）: 399-417.

[2] Flood I,Kartam N. Neural networks in civil engineering,I:Principles and understanding. Comp Civ Eng,1994, 8（2）: 132-148.

[3] Freeman J, Skapura D. Neural Networks:Algorithms, Applications,and Programming Techniuques. USA, Andison-Wesley Publ. Comp, 1991.

[4] McCulloch J, Robinson M. History of forest hydrology. Journal of Hydrology,1993, 150（2）: 189-216.

[5] Smith J,Eli R. Neural-network models of rainfall-runoff process. Journal of water resources planning and management,1995, 121（6）: 499-508.

[6] Nachimuthu Karunanithi, William J Grenney, Darrell Whitley, et al. Neural networks for river flow prediction. Journal of Computing in Civil Engineering,1994, 8（2）: 201-220.

[7] Lorrai M,Sechi G. Neural nets for modelling rainfall-runoff transformations. Water resources management,1995, 9（4）: 299-313.

[8] Martin T. Neural Network Design[M].北京：机械工业出版社, 2002.

[9] 高隽. 人工神经网络原理及仿真实例[M]. 北京：机械工业出版社, 2002.

[10]尹准生,孙长忠,赵明扬.黄土高原半干旱区油松人工林枯落物截留雨量模拟研究[J].林业科学研究, 2015,28（3）: 417-420.

[11]黄洪峰. 土壤-植物-大气相互作用原理及模拟研究[M]. 北京：气象出版社, 1997.

[12]蒋宗礼. 人工神经网络导论[M]. 北京：高等教育出版社, 2001.

[13]李祚泳,彭荔红. BP网络学习能力与泛化能力满足的不确定关系式[J]. 中国科学,2003, 33（10）: 887-895.

[14]盛仲飙,同晓荣. BP神经网络在曲线拟合中的应用[J].科学技术与工程,2011,11（28）:1671- 1815.

[15]孙长忠,陈海滨. 黄土高原林业资源开发与发展问题的探讨[J]. 西北林学院学报,1995, 10（增）: 174-179.

[16]孙长忠, 黄宝龙, 陈海滨, 等. 黄土高原人工植被与其水分环境相互作用关系研究[J]. 北京林业大学大学学报,1998, 20（3）: 7-14.

[17]田景文,高美娟. 人工神经网络算法研究及其应用[M]. 北京：北京理工大学出版社, 2006.

[18]尹准生,孙长忠,赵明扬.黄土高原半干旱区油松人工林林冠截留模型及其参数特征研究[J].林业科学研究,2015,28（2）: 261-264.

[19]阎平凡. 人工神经网络的容量、学习与计算复杂性[J]. 电子学报,1995, （5）: 63-67.

[20]张立明. 人工神经网络的模型及其应用[M]. 上海：复旦大学出版社, 1993.

Artificial Neural Network model of soil moisture fluctuation ofplantations in Loess Plateau

Yin Zhunsheng,Tang Xiaojia,Lu Ji,Hong Yifeng,Chen Wei,Zuo Songyuan

Based on the actual local conditions ofin Loess Plateau, the input variables and output variables were selected and five hundred seventy-six groups of observed data ranging from 2012 to 2015 were applied to train and examine the neural network model. The results showed that the optimum network structure was 5:6:1,mean square error was 0.002 645,the general fitting accuracy was 96.78%,and the examined fitting accuracy was 94.44%.

The model of soil moisture changing; artificial neural network;; Loess Plateau

O157.5

A

1004-7743（2019）02-0067-04

2018-12-25