基于优势关系的程度粗糙直觉模糊集模型研究*

薛占熬，吕敏杰，韩丹杰，张 敏

1.河南师范大学 计算机与信息工程学院，河南 新乡 453007

2.“智慧商务与物联网技术”河南省工程实验室，河南 新乡 453007

1 引言

粗糙集由Pawlak[1]提出，主要用于处理不完备、不确定、不精确性信息。近年来，粗糙集发展非常迅速，被广泛应用到其他领域，且得到很多粗糙集扩展模型。比如，程度粗糙集[2]、粗糙直觉模糊集[3-5]和双论域粗糙集[6-7]等。Xue等[4]将覆盖、多粒度理论引入到粗糙直觉模糊集模型中，提出了多粒度覆盖粗糙直觉模糊集模型。薛占熬等[5]进一步研究和讨论了粗糙直觉模糊集截集理论，将其应用于评估小麦生长趋势。另外，刘慧等[7]用矩阵研究了双论域粗糙集，并通过实验验证该方法可简化下、上近似的表达方式。Lu等[8]讨论了二型模糊粗糙集的粒度结构，构造了双论域二型模糊粗糙集模型。Luo等[9]提出了双论域粗糙直觉模糊集模型，研究了相关的不确定性度量。双论域粗糙集[10]理论被应用于处理实际问题。Sun等[10]结合了多粒度模糊粗糙集与双论域理论，构造了基于双论域的多粒度模糊粗糙集模型，应用其处理衣服排序多标准群体决策问题。

Yao等[2]于1996年提出了粗糙集的扩展模型——程度粗糙集。很多学者对程度粗糙集[11-15]进行了研究，取得了丰硕的成果。张贤勇等[11]从广义程度粗糙集出发，定义了程度粗糙集，且对程度粗糙集的内部构造、算子进行了研究，同时讨论了知识约简的内容。Huang等[12]将直觉模糊β邻域理论与直觉模糊β覆盖粗糙集结合，提出了直觉模糊程度覆盖粗糙集理论。沈家兰等[13]和汪小燕等[14]分别构造了可变程度多粒度粗糙集和不完备加权程度多粒度粗糙集。另外，以程度粗糙集和双论域为基础，阎瑞霞等[15]研究了双论域粗糙集的不确定性度量。Huang等[16]以直觉模糊信息系统为基础，研究了优势关系，分别提出了优势直觉模糊信息系统的概念和优势直觉模糊信息系统的广义优势粗糙集模型。

在直觉模糊序信息系统上，本文将程度粗糙集与粗糙直觉模糊集结合，引入优势关系，构造出基于优势关系的I型、II型程度粗糙直觉模糊集模型。在此基础上，结合双论域理论，构造了基于优势关系的I型、II型双论域程度粗糙直觉模糊集模型。并进一步研究了基于优势关系的双论域程度粗糙直觉模糊集的模糊熵。最后，通过实例分析验证了所提模型的有效性。

2 基础知识

为更好地处理不确定性问题，Yao等[2]提出了程度粗糙集模型。Rizvi等[17]于2002年提出了粗糙直觉模糊集模型及直觉模糊信息系统。具体定义如下：

定义1[2](U,R)为近似空间，设k是非负整数，R是论域U上的等价关系，X⊆U，在论域U上定义X关于k的下近似和上近似分别为：

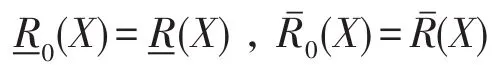
定义2[17]设(U,R)为一个近似空间，R是U上的一个等价关系，设B是一个直觉模糊集，则B关于(U,R)的一对下近似和上近似分别为：

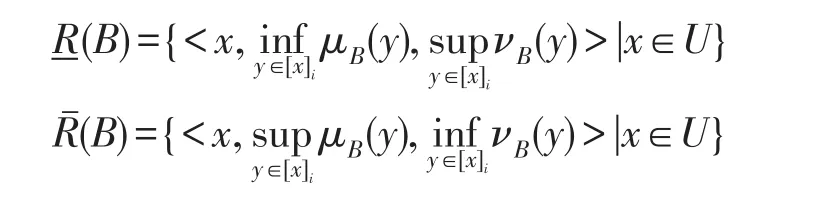
定义3[17]直觉模糊信息系统是一个四元组(U,A,V,f)，其中U是一个非空有限论域，A是一个非空有限属性集，V是所有直觉模糊值组成的集合，信息函数f是一个从U×A到V的映射，使得对任意的x∈U和a∈A，有fa(x)=(μa(x),νa(x))∈V，其中，ua(x):U→[0,1],νa(x):U→[0,1]分别称为论域U中元素x关于属性a的隶属度和非隶属度。显然A(x)= {＜x,μa(x),νa(x)＞|x∈U}，是论域U上的一个直觉模糊集。

定义4[18]设(U,A,V,f)是一个直觉模糊信息系统，若在某个属性值域上建立偏序关系，则称这个属性为一个准则。当直觉模糊信息系统中所有的属性都为准则时，则称该系统为直觉模糊序信息系统，记作I≥=(U,A,V,f)。

3 基于优势关系的程度粗糙直觉模糊集模型

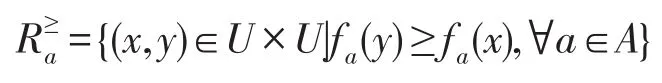
若记

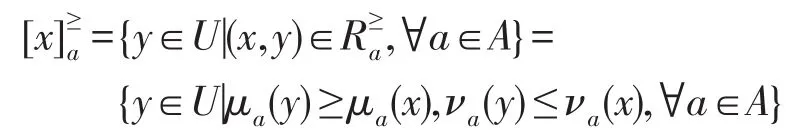
3.1 基于优势关系的I型程度粗糙直觉模糊集

定义6设(U,A,V,f)是一个直觉模糊序信息系统，设X⊆U，a∈A，R是论域U上的等价关系，集合X关于知识R形成程度粗糙集。设μB(x)、νB(x)为论域U上元素x关于属性a形成的一个直觉模糊集B的隶属度和非隶属度，则关于k（k为非负整数）的基于优势关系的I型程度粗糙直觉模糊集的下、上近似定义为：

当k≥1时：

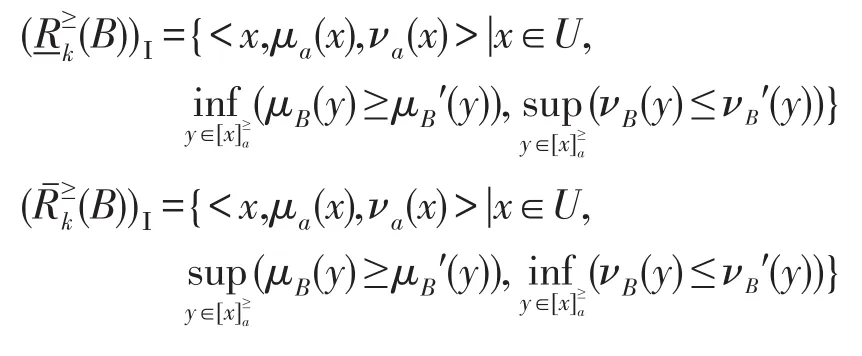
其中：

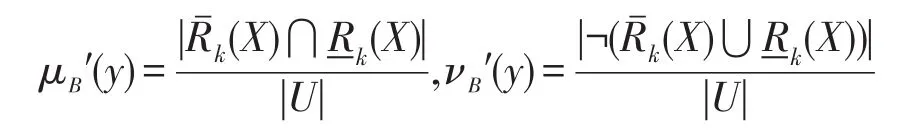
当k=0时，程度粗糙集退化为经典粗糙集，则μB′(y)和νB′(y)退化成由经典粗糙集计算的阈值，此时模型仍具有有效性。

3.2 基于优势关系的II型程度粗糙直觉模糊集

定义7设(U,A,V,f)是一个直觉模糊序信息系统，其中X⊆U，a∈A，R是论域U上的等价关系，集合X关于知识R形成程度粗糙集。B为论域U上元素x关于属性a形成的直觉模糊集，则关于k（k为非负整数）的基于优势关系的II型程度粗糙直觉模糊集定义为：

当k≥1时：

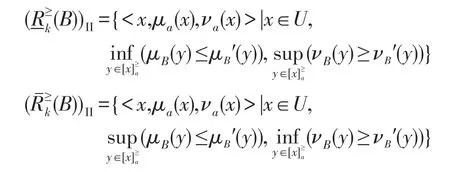
其中：

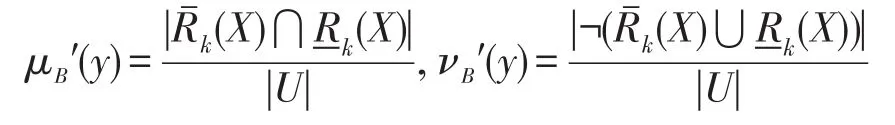
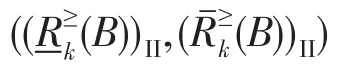
当k=0时，程度粗糙集退化为经典粗糙集，则μB′(y)和νB′(y)就退化成由经典粗糙集构造的阈值，此时模型仍具有有效性。

例1设(U,A,V,f)是一个直觉模糊序信息系统，其中a∈A,∀B∈IF(U),X⊆U，其中论域U上的划分C={{x1,x2,x5},{x3,x4},{x8,x9},{x6,x7,x10}},X={x3,x6,x8,x10}。设论域U上的直觉模糊集B为：

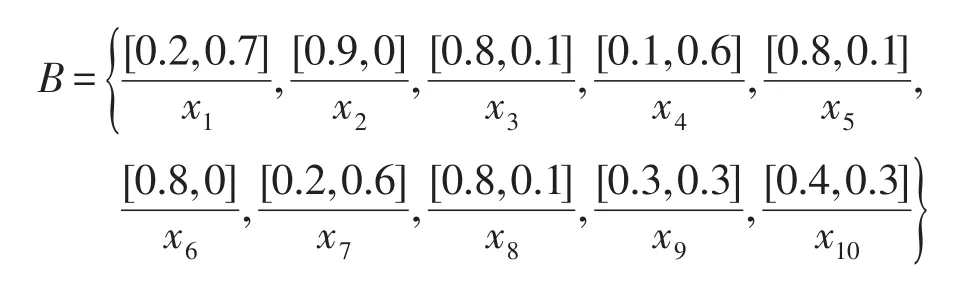
计算B的基于优势关系的I型、II型程度粗糙直觉模糊集。

步骤1设k=1，则可以计算出μB′(y)和νB′(y)为：

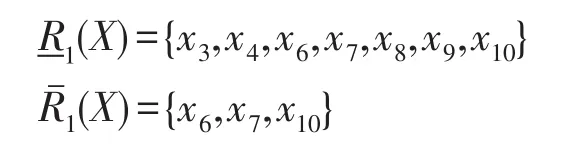
根据

得μB′(y)=0.3 ，νB′(y)=0.3 。

步骤2根据定义6，计算基于优势关系的I型程度粗糙直觉模糊集模型的隶属度如下：

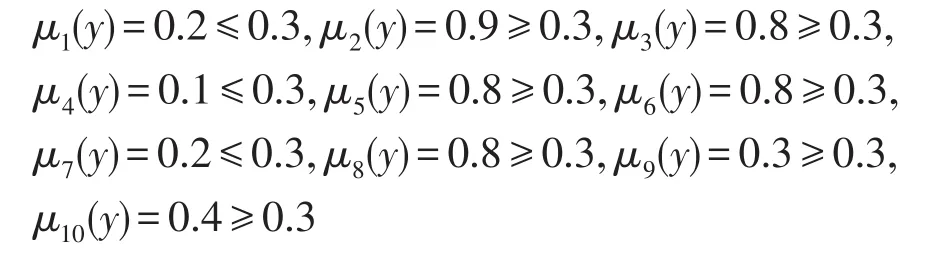
根据以上计算可以选出满足条件的隶属度：

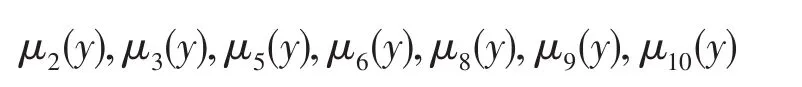
同理，可以计算出非隶属度，过程略。

步骤3对基于优势关系的I型程度粗糙直觉模糊集模型，根据定义5，可以得其优势类，如下所示：

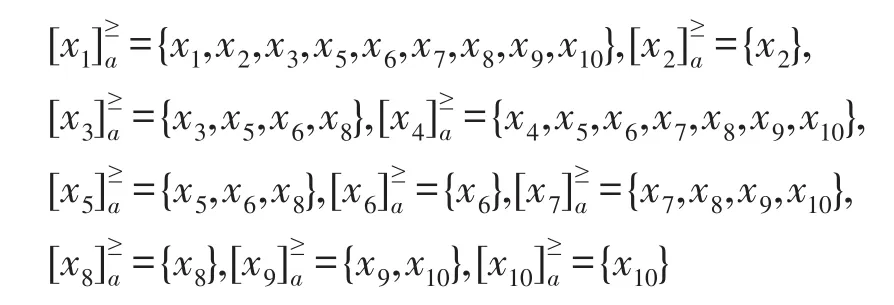
步骤4根据定义6，则可得基于优势关系的I型程度粗糙直觉模糊集中满足μB(y)≥μB′(y),νB(y)≤νB′(y)的优势类如下：

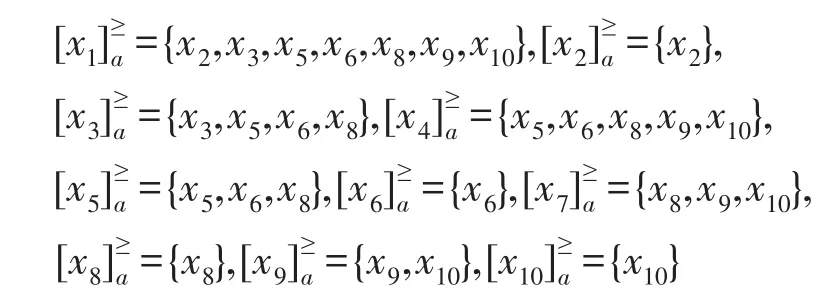
步骤5计算B的基于优势关系的I型程度粗糙直觉模糊集模型：

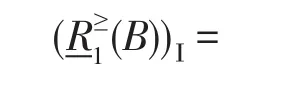
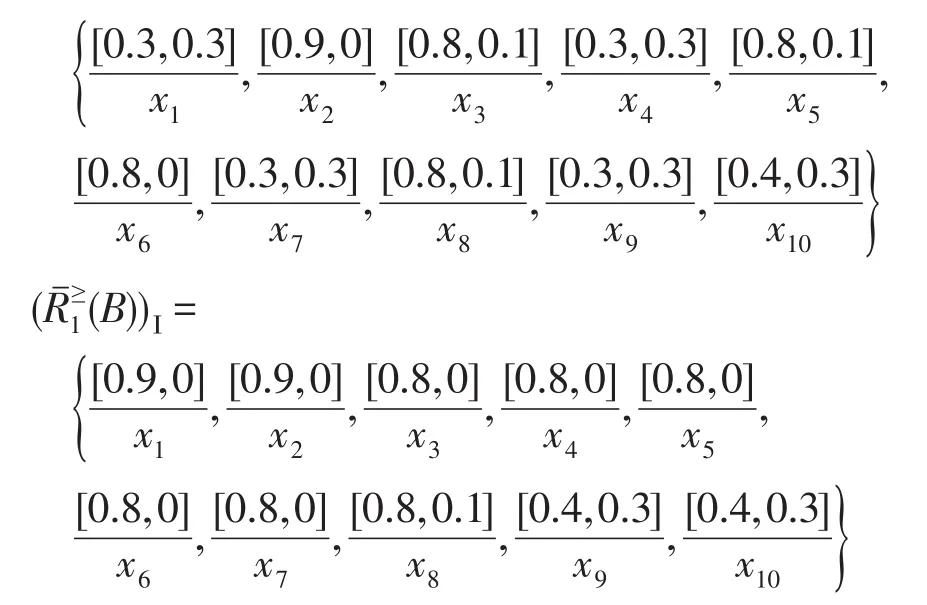
步骤6重复步骤2～4，根据定义7，可以计算出B的基于优势关系的II型程度粗糙直觉模糊集。

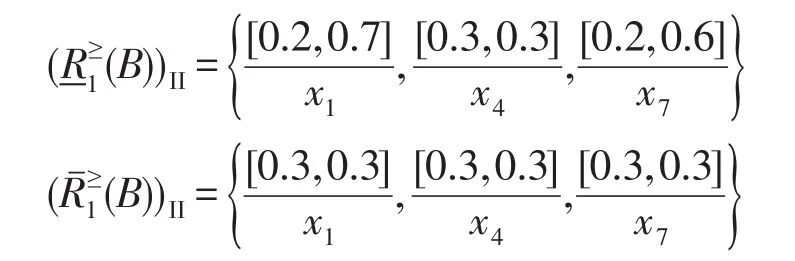
定理1设(U,A,V,f)是一个直觉模糊序信息系统，设a,b∈A，A,B∈IF(U)，则基于优势关系的I型、II型程度粗糙直觉模糊集的下、上近似具有以下性质：

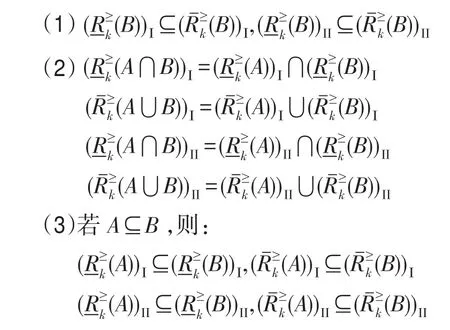
证明

（1）根据定义6、定义7易证，过程略。

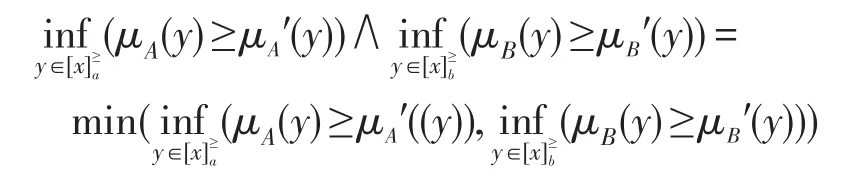
因μA⋂B′(y)、μA′(y)、μB′(y)的值是根据R-程度粗糙集得出，故μA⋂B′(y)=μA′(y)=μB′(y)，于是

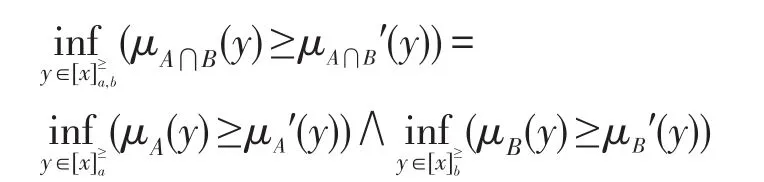
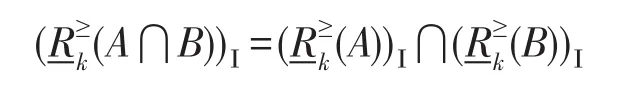
这里仅证明第一个性质，同理可证余下的性质，过程略。

4 基于优势关系的双论域程度粗糙直觉模糊集模型

在第3章中，提出了基于优势关系的I型、II型程度粗糙直觉模糊集模型。在本章中，将基于优势关系的I型、II型程度粗糙直觉模糊集模型与双论域粗糙直觉模糊集模型融合，构造出基于优势关系的I型、II型双论域程度粗糙直觉模糊集模型。

定义8[20]设(U,V,R)为一般近似空间，分别定义映射Rs:U→P(V)和Rp:V→P(U)如下：

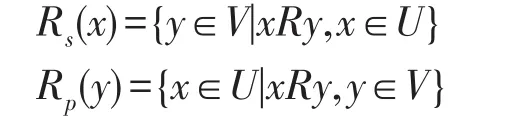
其中，Rs(x)、Rp(y)分别表示论域U中的元素x关于R的后继邻域，论域V中的元素y关于R的前继邻域。

定义9[21]设(U,V,R)为一般近似空间，对于任意的X⊆U和Y⊆V，则X和Y的下、上近似分别为：

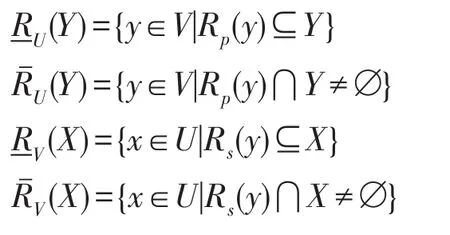
定义10[22-23]设R是U到V上的一般二元关系，则有：

（1）对于任意的x∈U，存在一个y∈V，R(x,y)=1，则R是串行的。

（2）对于任意的y∈V，存在一个x∈U，满足R(x,y)=1，则R是逆串行的。

定义11[10]设(U,V,R)是双论域一般近似空间，对任意的A∈IF(U)，B∈IF(V)，则直觉模糊集A、B的下、上近似为：

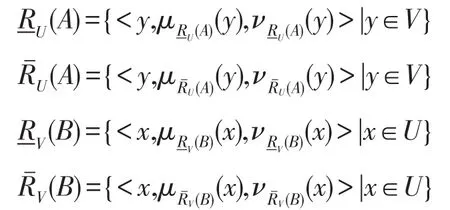
其中：

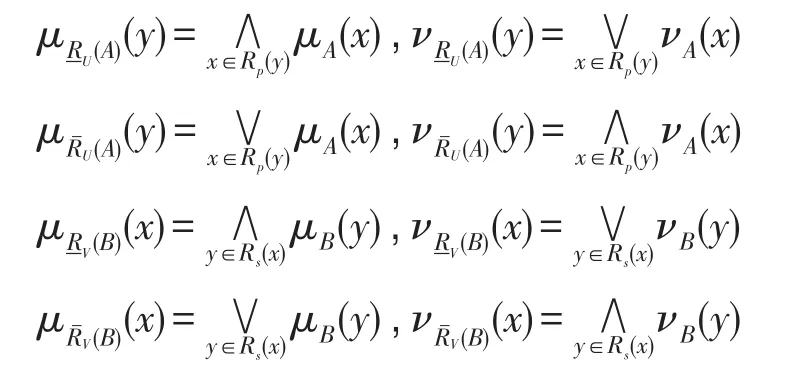
4.1 基于优势关系的I型双论域程度粗糙直觉模糊集

定义12设(U,V,AU,AV,VAU,VAV,fU,fV)是基于双论域的直觉模糊序信息系统，其中U、V为两个论域，其中AU、AV为U、V上的非空属性集。信息函数fU、fV分别为U×AU和V×AV到VAU和VAV的映射，对a∈AU,x∈U和b∈AV,y∈V，有fa(x)=(μa(x),νa(x))∈VAU和fb(y)=(μb(y),νb(y))∈VAV。A、B关 于 属 性a、b在U、V上是直觉模糊集。基于双论域的直觉模糊序信息系统的优势关系可以定义如下：

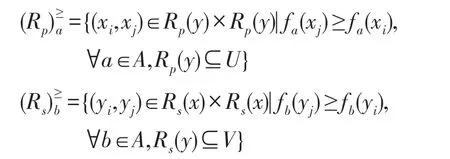
若记：

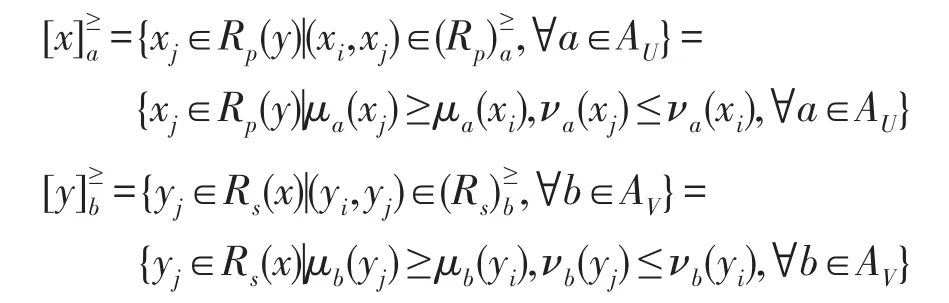
定义13设(U,V,AU,AV,VAU,VAV,fU,fV)是基于双论域的直觉模糊序信息系统，且X⊆U,Y⊆V。RU、RV分别是论域U、V上的等价关系，集合X、Y关于知识RU、RV构成程度粗糙集。对于任意的A∈IF(U),B∈IF(V)，则基于优势关系的I型双论域程度粗糙直觉模糊集的下、上近似分别为：

当k≥1时：

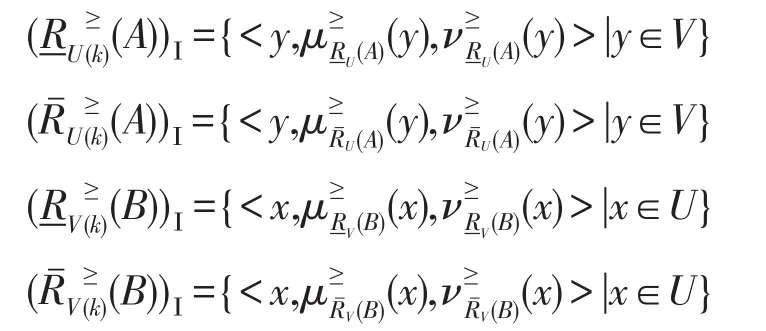
其中：

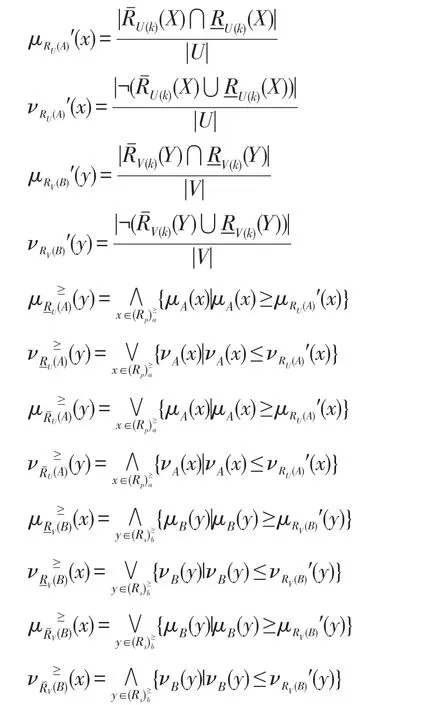
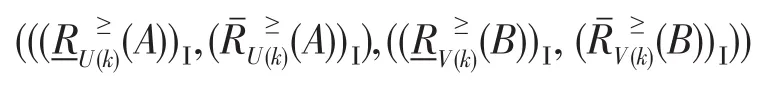
当k=0时，程度粗糙集退化为经典粗糙集，则μRU(A)′(x)、νRU(A)′(x)和μRV(B)′(y)、νRV(B)′(y)就退化为由经典粗糙集构造的阈值，此时模型仍具有有效性。

4.2 基于优势关系的II型双论域程度粗糙直觉模糊集

定义14设(U,V,AU,AV,VAU,VAV,fU,fV)是基于双论域的直觉模糊序信息系统，且X⊆U,Y⊆V。RU、RV分别是论域U、V上的等价关系，集合X、Y关于知识RU、RV构成程度粗糙集。对于任意的A∈IF(U),B∈IF(V)，则基于优势关系的II型双论域程度粗糙直觉模糊集的下、上近似定义为：

当k≥1时：

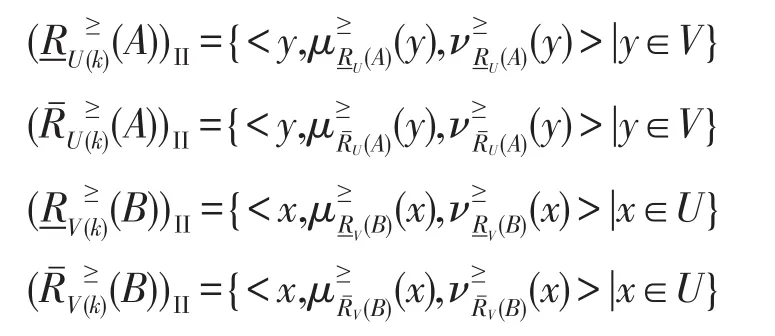
其中：

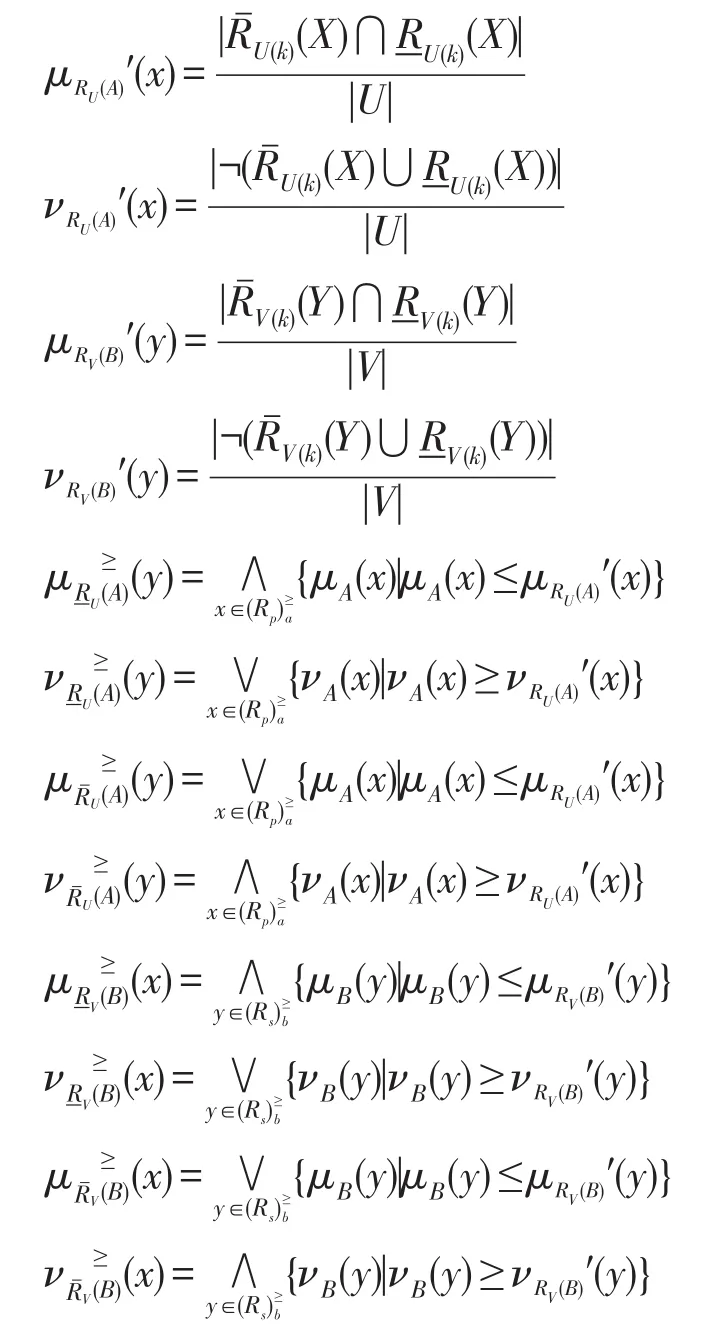
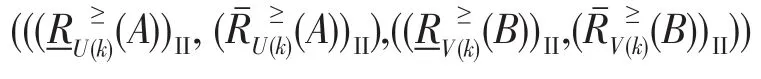
当k=0，程度粗糙集退化为经典粗糙集，则μRU(A)′(x)和νRU(A)′(x)、μRV(B)′(y)和νRV(B)′(y)就退化为由经典粗糙集模型计算的阈值，此时模型仍具有有效性。

定理2设(U,V,AU,AV,VAU,VAV,fU,fV)是基于双论域的直觉模糊序信息系统，且X⊆U,Y⊆V。RU、RV分别是论域U、V上的等价关系，集合X、Y关于知识RU、RV构成程度粗糙集。对于任意的A1,A2∈IF(U),B1,B2∈IF(V),则基于优势关系的I型、II型双论域程度粗糙直觉模糊集具有如下性质：

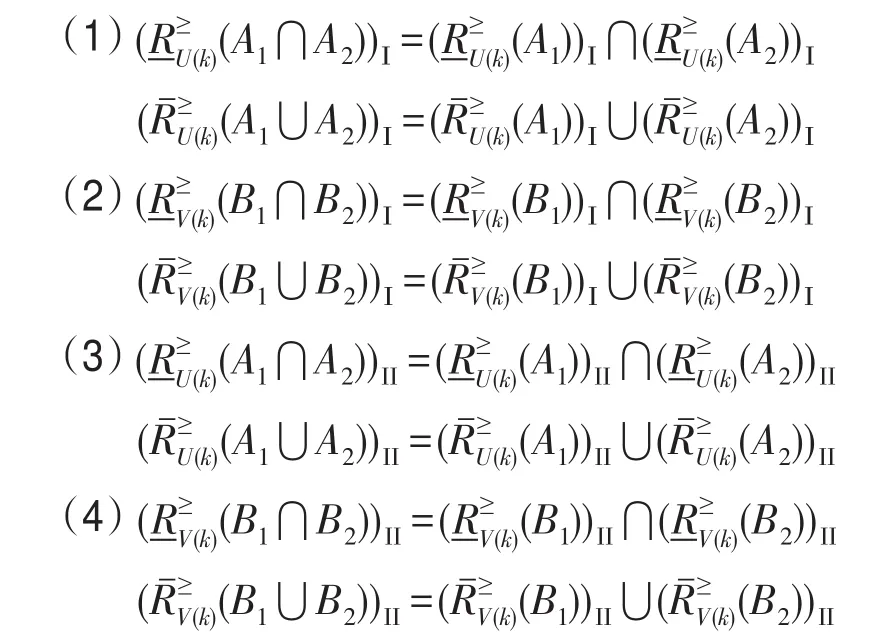
证明

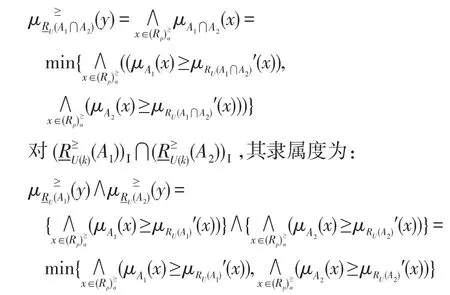
因μRU(A1⋂A2)′(x)、μRU(A1)′(x)、μRU(A2)′(x)的值是根据RU-程度粗糙集得出，故μRU(A1⋂A2)′(x)=μRU(A1)′(x)=μRU(A2)′(x)，于是

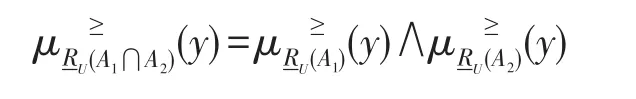
同理，可知非隶属度有如下关系：

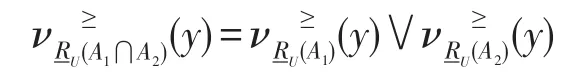
同理可证（1）中余下性质及（2）～（4）的性质。

定理3设(U,V,AU,AV,VAU,VAV,fU,fV)是基于双论域的直觉模糊信息系统，且X⊆U,Y⊆V。RU、RV分别是论域U、V上的等价关系，集合X、Y相对知识RU、RV构成程度粗糙集。对于任意的A1,A2∈IF(U),B1,B2∈IF(V),A1⊆A2,B1⊆B2，则基于优势关系的I型、II型双论域程度粗糙直觉模糊集具有如下性质：

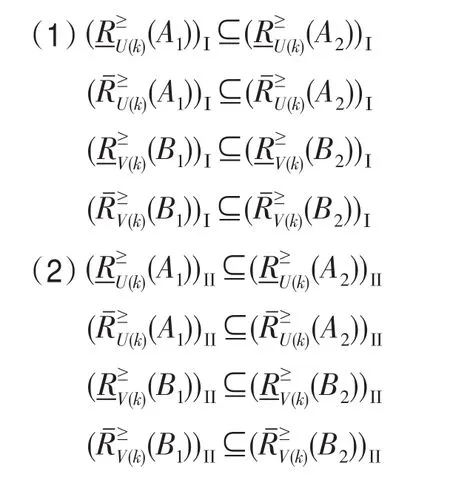
证明根据定义13、定义14，易知定理3成立。

4.3 基于优势关系的双论域程度粗糙直觉模糊集的模糊熵

定理 4[24]设论域U={x1,x2,…,xn},A={＜x,μA(xi),νA(xi)＞|xi∈X}是定义在U上的一个直觉模糊集，A的模糊熵E(A)为：

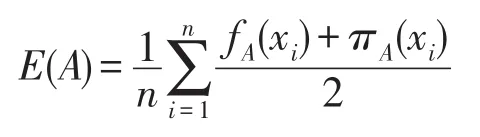
其中，fA(xi)=1-|μA(xi)-νA(xi)|,πA(xi)=1-μA(xi)-νA(xi)。

定义15设(U,V,AU,AV,VAU,VAV,fU,fV)是基于双论域的直觉模糊序信息系统，且X⊆U,Y⊆V。RU、RV分别是论域U、V上的等价关系，集合X、Y关于知识RU、RV构成程度粗糙集。则对于任意的A∈IF(U),B∈IF(V)，则直觉模糊集A的模糊熵可定义为：

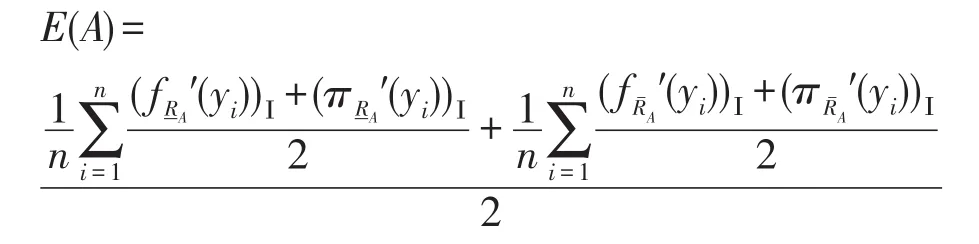
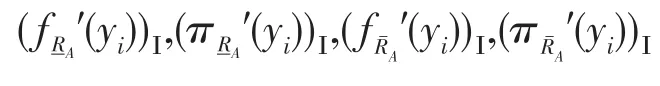
另外，可类似定义直觉模糊集B的模糊熵及基于优势关系的II型双论域程度粗糙直觉模糊集的模糊熵。

5 实例分析

设U和V分别表示症状和疾病的集合。A1、A2、A3分别由1、2、3号患者的症状构成3个直觉模糊集。μ′(x)、ν′(x)通过程度粗糙集计算得出。

设U={x1,x2,x3,x4,x5,x6},V={y1,y2,y3,y4,y5,y6}分别为6种症状与疾病的集合，其中，症状与疾病的关系可见表1。R是U×V上的一般二元关系，假设对于任意的xi∈U，存在一个yi∈V，满足R(xi,yj)=1，按定义，理解为如表现症状xi，则患有疾病yj。根据编号1、2、3患者的症状，可以分别得到每位患者的症状的3个划分如下：C1={{x1,x2},{x4},{x3,x5,x6}},C2={{x1},{x2,x3,x4},{x5,x6}},C3={{x1,x2},{x3,x5},{x4,x6}}。设X={x4,x5,x6}。

Table1 Relation of symptoms and diseases表1 症状与疾病的关系

步骤1首先设k为1，由C1、C2、C3的划分，分别可得如下所示的程度粗糙集：

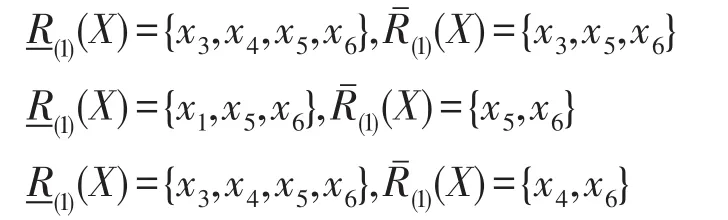
由定义13、定义14，可得μ′(x)、ν′(x)如下：

步骤2由表1，可以得到yi的前继邻域：

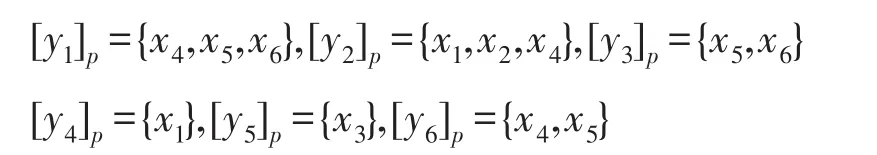
步骤3根据基于双论域的直觉模糊序信息系统的优势关系的定义可得A1、A2、A3的优势类为：

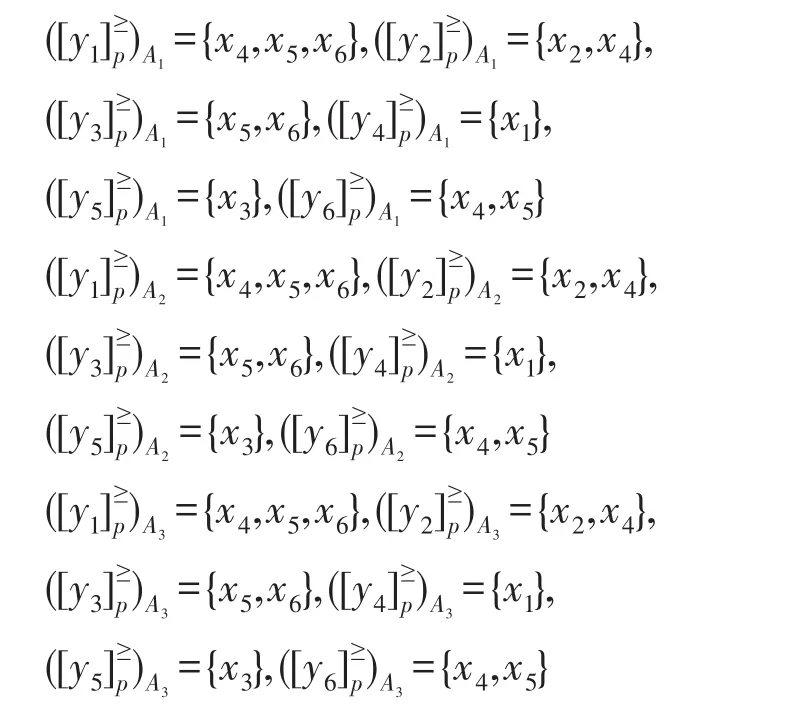
步骤4根据步骤1～步骤3，计算每位患者的基于优势关系的I型双论域程度粗糙直觉模糊集，结果如下所示：

步骤5根据步骤1～步骤3，计算基于优势关系的II型双论域程度粗糙直觉模糊集如下：

步骤6根据1～3号患者的基于优势关系的I、II型双论域程度粗糙直觉模糊集的结果，分析3位患者的病情，可得以下的结论：

（1）根据I型双论域程度粗糙直觉模糊集可知：1号患者患y1、y2、y3、y4、y6疾病确定为 (y1,0.8,0),(y2,0.6,0),(y3,0.8,0),(y4,0.9,0),(y6,0.8,0)，患有y1、y2、y3、y4、y6疾病可能为(y1,0.8,0),(y2,0.8,0),(y3,0.8,0),(y4,0.9,0),(y6,0.8,0)。然后，根据II型双论域程度粗糙直觉模糊集可知：患有y5疾病确定为(y5,0.2,0.7)，患y5疾病可能为(y5,0.2,0.7)。通过分析以上两个模型的结果，确定1号患者没有患y5疾病。

（2）根据I型双论域程度粗糙直觉模糊集可知：2号患者患y1、y3、y4、y5、y6疾病确定为 (y1,0.4,0.5),(y3,0.4,0.5),(y4,0.8,0.2),(y5,0.6,0.4),(y6,0.4,0.5)，患y1、y3、y4、y5、y6疾病可能为 (y1,0.7,0.2),(y3,0.7,0.2),(y4,0.8,0.2),(y5,0.6,0.4),(y6,0.4,0.5)。然后，根据II型双论域程度粗糙直觉模糊集可知：患y2、y6疾病确定为(y2,0.2,0.6),(y6,0.2,0.5)，患y2、y6疾病可能为(y2,0.2,0.5),(y6,0.2,0.5)。通过分析以上两个模型的结果，确定2号患者没有患y2疾病。

（3）根据I型双论域程度粗糙直觉模糊集可知：3号患者患y1、y3、y4、y6疾病确定为(y1,0.5,0.2),(y3,0.5,0.2),(y4,0.7,0.2),(y6,0.5,0.2),患有y1、y3、y4、y6疾病可能为(y1,0.6,0.2),(y3,0.6,0.2),(y4,0.7,0.2),(y6,0.5,0.2)。然后，根据II型双论域程度粗糙直觉模糊集可知：患有y1、y2、y5、y6疾病确定为 (y1,0.3,0.6),(y2,0.3,0.6),(y5,0.1,0.6),(y6,0.3,0.6) ，患y1、y2、y5、y6疾病可能为(y1,0.3,0.6),(y2,0.3,0),(y5,0.1,0.6),(y6,0.3,0.6)。通过分析以上两个模型的结果，确定3号患者没有患y2、y5疾病，由于y1、y6种疾病在I、II型双论域程度粗糙直觉模糊集模型中都有出现，故还需进一步确认。

步骤7由定义15，可计算基于优势关系的I、II型双论域程度粗糙直觉模糊集的模糊熵，这里仅计算基于优势关系的I、II型双论域程度粗糙直觉模糊集A1的模糊熵，并将其与原模型的模糊熵作比较。

此为计算的原模型A1的模糊熵：

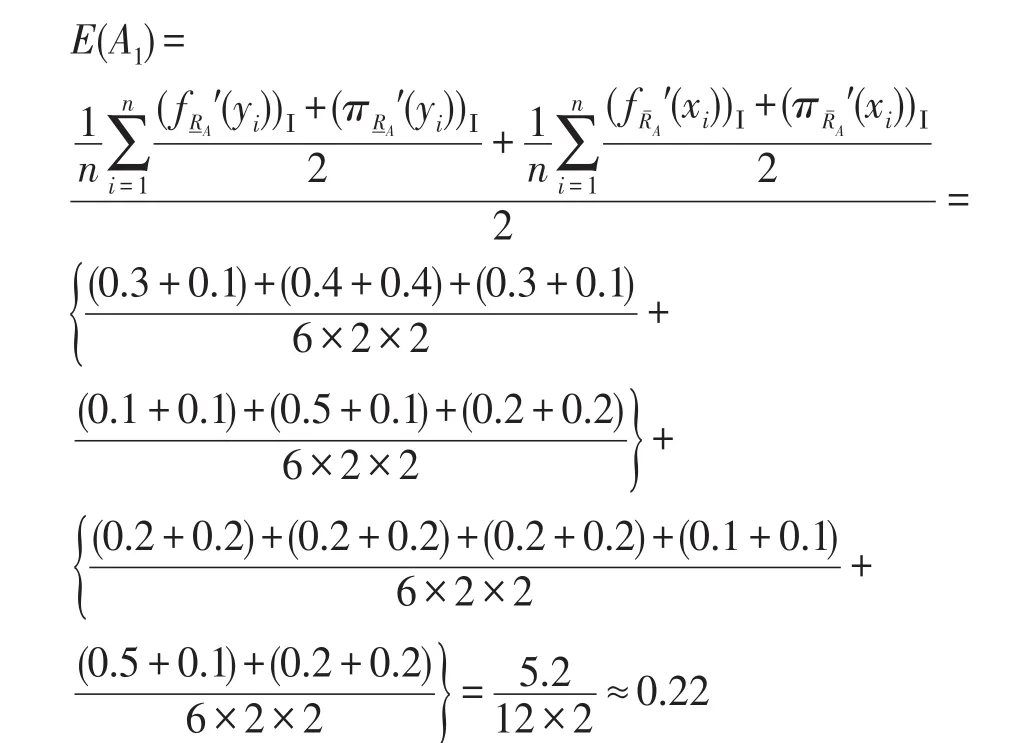
故，可得基于优势关系的I型双论域程度粗糙直觉模糊集A1的模糊熵为：

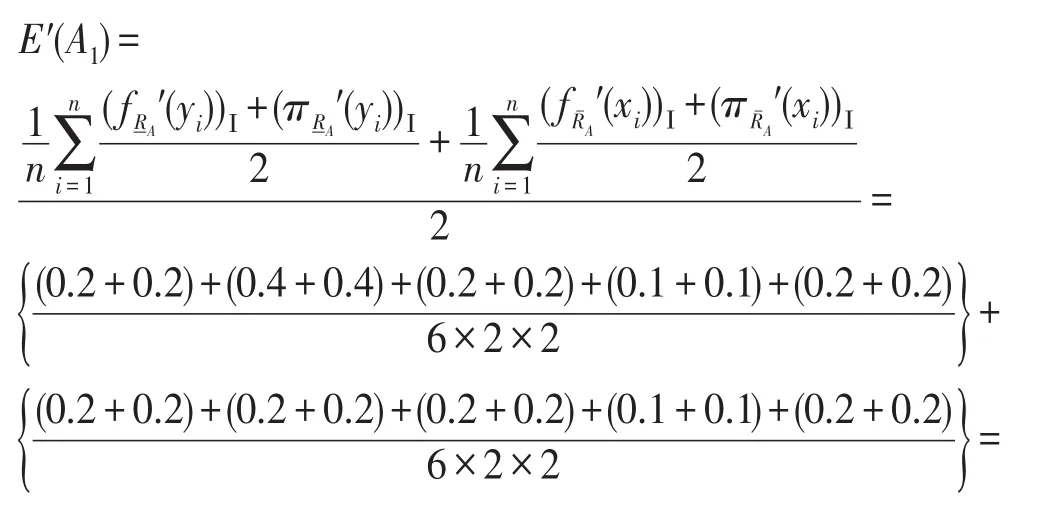
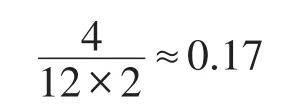
由以上的计算可得：E′(A1)≤E(A1)。

同理，可以计算基于优势关系的II型双论域程度粗糙直觉模糊集的模糊熵值。

由以上分析可知，当k=1时，根据基于优势关系的I、II型双论域程度粗糙直觉模糊集模型，确定1号患者没有患y5疾病；确定2号患者没有患y2疾病；确定3号患者没有患y2、y5疾病，y1、y6种疾病还需进一步确认。通过以上的模型分析，可以排除患者患某种疾病，这样可以减少患者进行不必要的检查，也有利于医生合理地安排其他疾病的诊断治疗，因此基于优势关系的I、II型双论域程度粗糙集模型具有一定的现实意义。且实例证明了模型的模糊熵比原模型的小。另外，可以根据实际需要设置μ′(y)和ν′(y)的大小，来满足现实需求。

6 结束语

经典粗糙直觉模糊集模型中只取与x相关的集合中的最小/最大隶属度，而介于最小/最大之间的隶属度与非隶属度并没有起作用，通过与两个阈值比较，让介于最小/最大之间的隶属度与非隶属度发挥作用。本文基于粗糙直觉模糊集、双论域粗糙直觉模糊集理论，提出了基于优势关系的I、II型程度粗糙直觉模糊集和基于优势关系的I、II型双论域程度粗糙集直觉模糊集模型。同时，分析讨论了各个模型的性质。最后通过实例对模型进行分析验证。下一步的工作是对区间模糊集与程度粗糙集的相关内容进行研究与讨论。