堤岸稳定性影响因素敏感性评价
2019-06-18郑丽霞
郑丽霞
(沈阳市苏家屯区浑南灌区管理处,辽宁 沈阳 110101)
堤岸工程是一项重要的防洪工程,尤其是夏季暴雨、台风的到来,堤岸可有效防止洪水灌入城镇。堤岸工程的稳定性是保证人民安全的关键因素。许多专家学者对堤岸稳定性进行了研究。赵宇坤等[1]使用饱和—非饱和理论研究了汛期水位骤升骤降对堤岸稳定性的影响,分析了坡体内部水位的变化,绘制不同工况下堤岸稳定状态图。张芳枝等[2]通过数值模拟手段研究河流冲刷对堤岸稳定性的影响,结果表明:坡脚位置渗流流速最大,冲刷造成岸坡塑性区范围增大,降低了堤岸稳定性。刘动等[3]通过现场实测资料使用神经网络模型对河流冲刷作用下河床、堤岸变形进行预测研究。马崇武等[4]通过数值模拟研究堤岸稳定性最小时的水位值,对工程建设意义重大。肖瑶等[5]考虑岩土体强度劣化对岸坡稳定性的影响,当岩土体强度劣化达到30%时,岸坡稳定性达到临界破坏值。陈将宏等[6]选取了四个因素作为评价岸坡稳定性的影响因素并确定其权重。
在实际工程中,堤岸工程的失稳破坏往往不是单一因素决定的,影响其稳定性的是多个因素的组合作用。利用实际工程直接对单一因素的权重进行分析具有明显的局限性。因此,采用正交试验的方法对影响因素敏感性进行分析。该方法可进行多次试验,选取具有客观代表性的组合进行试验,可有效提高试验的效率。随着计算机技术的快速发展,人工智能不断地用于工程计算方面,可有效逼近非线性计算结果,有较强的适用性[7]。选取了土体强度(X1黏聚力,X2内摩擦角,X3坡比,X4坡高),边界因素(X5墙前水位,X6墙后水位,X7墙后荷载)等7个指标作为堤岸稳定性评价的影响因素,进行敏感性分析。
1 堤岸稳定性影响因素敏感性分析
1.1 BP神经网络模型
按照结构方面分析,可以将神经网络分成输入层、隐含层和输出层三个层次(见图1)。输入层和隐含层以及隐含层和输出层之间包含有大量的神经元。不同的神经元具备不同的权值,这些权值可以作为神经网络定量计算时的连接强度。

(从上至下分别代表输入层、隐含层、输出层)图1 BP神经网络模型
在使用神经网络模型进行分析计算的过程中,从输入层输入数据,通过隐含层的分析计算后,输入的数据变为非线性数据,最后从输出层输出结果,数据的这种传输过程即为数据的正方向传输[8]。通过对比输出结果与既定目标之间的差距可以得知神经网络的计算精度,当计算精度达不到目标要求时,通过反向传输来重新调整阈值。经过多次试验,调整输出结果直至精度可以满足要求。这种反向传播调整试验精度就是神经网络的学习过程[9]。
计算过程如下。定义函数γ:
(1)
式中:n为输出层内包含的所有单元的总数;y为目标输出值;y′为实际输出值。
每个连接强度即权值的修正公式如式(2)所示。
(2)
式中:ωi为输入数据x到隐含层i的权重;α为神经网络模型系统学习的工作效率;Ii为第i个隐含层的传输函数。
输入层与隐含层之间一般采用Sigmoid函数进行数据的传输,该函数输入值为(-∞,+∞),输出值区间范围为(0,1),这样的输入输出值范围有助于模型在进行训练学习过程中进行精度的对比。Sigmoid函数如式(3)所示。
f(x)=(1+e-x)-1
(3)
式中:x为输入值。
隐含层到输出层之间的关系满足Purelin函数,即输出值与输入值相等。
学习训练工作完成后,精度满足设计要求时,该模型即可用于实际工作。
1.2 基于Garson的参数敏感性分析方法
在神经网络的学习训练过程中,输入层—隐含层、隐含层—输出层之间的连接强度即权值确定了不同单元的输入值对输出值影响的程度。一个单元对输出结果影响程度的大小即为该单元对输出结果影响的敏感性。因此,可以使用以下算法表达这种影响程度(式4)。
(4)
式中:Ri k为输入值的对输出值的影响程度;Wi j为输入层i—隐含层j的连接强度即权值;Wj k为隐含层j—输出层k的连接强度即权值;N、M分别为输入层、输出层的总数,2N+M为隐含层总数。
2 工程应用
以某段堤岸为例,计算稳定性影响因子的敏感因素。经过现场调查和室内试验获取该地区各影响因素取值和岩土体力学参数。黏聚力为15 kPa,内摩擦角为15°,坡比为2.1,坡高5 m,墙前水位3 m,墙后水位1 m,墙后荷载5 kPa。查阅相关资料单影响因子的评价等级分级如表1所示。

表1 指标评价等级
为保证计算方便可靠、快捷,采用正交试验。各指标作为输入层,通过组合计算得到的安全系数作为输出层。正交试验结果如表2所示。
将试验数据输入模型中,输入层的神经元共有7个,输出层神经元只有1个,因此,当隐含层神经元个数取15个时神经网络学习训练效果最好。神经网络不停地学习至误差达到目标时可停止学习,此时可获取输入值与输出值的关系。引入Garson算法对权值矩阵进行相应的处理,获取各输入神经元的相对贡献量。
通过表3可以看出堤岸稳定性对各因素的敏感程度按照强弱顺序如下:X1黏聚力,X2内摩擦角,X3坡比,X4坡高,X5墙前水位,X6墙后水位,X7墙后荷载。
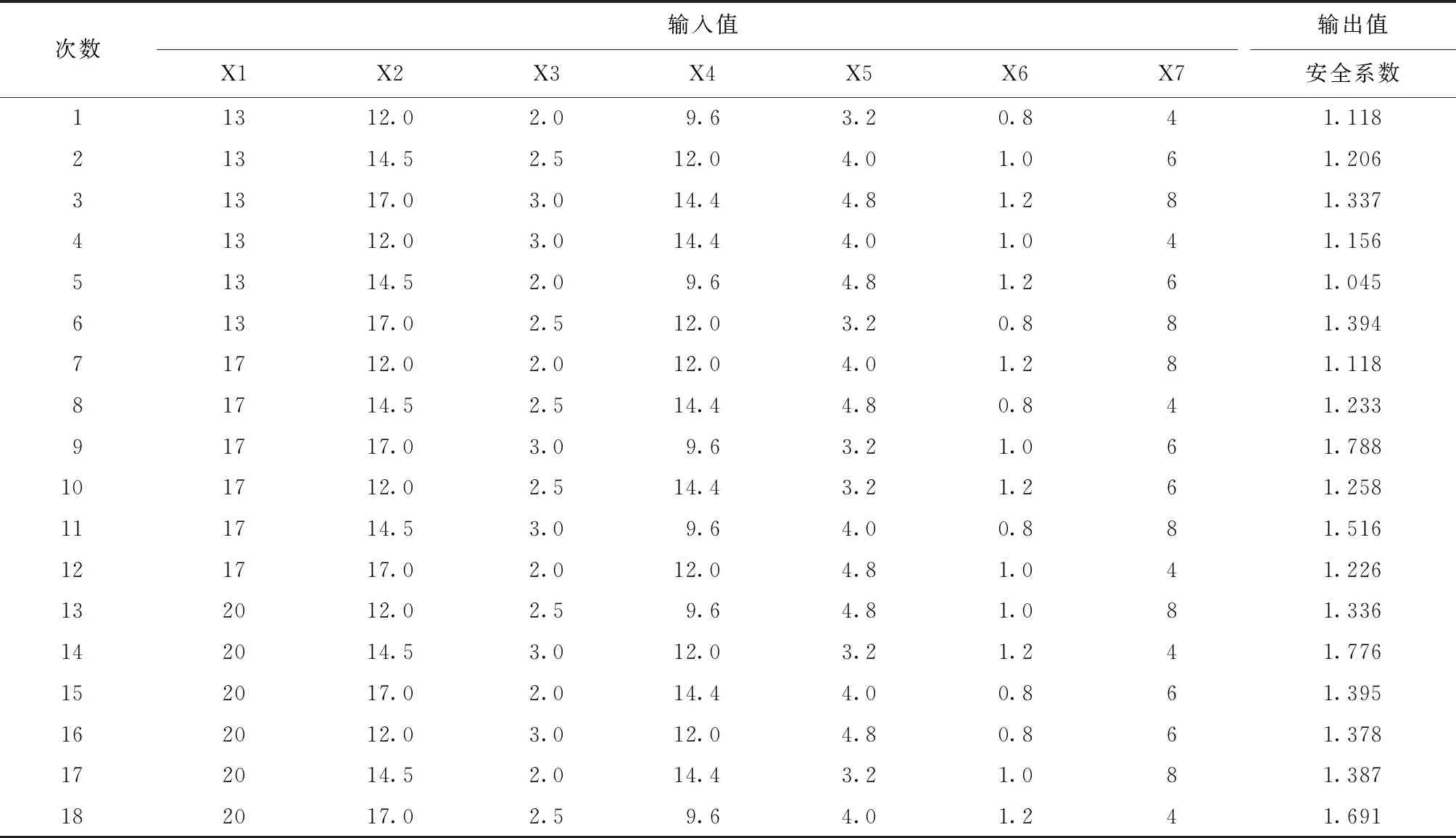
表2 正交试验结果
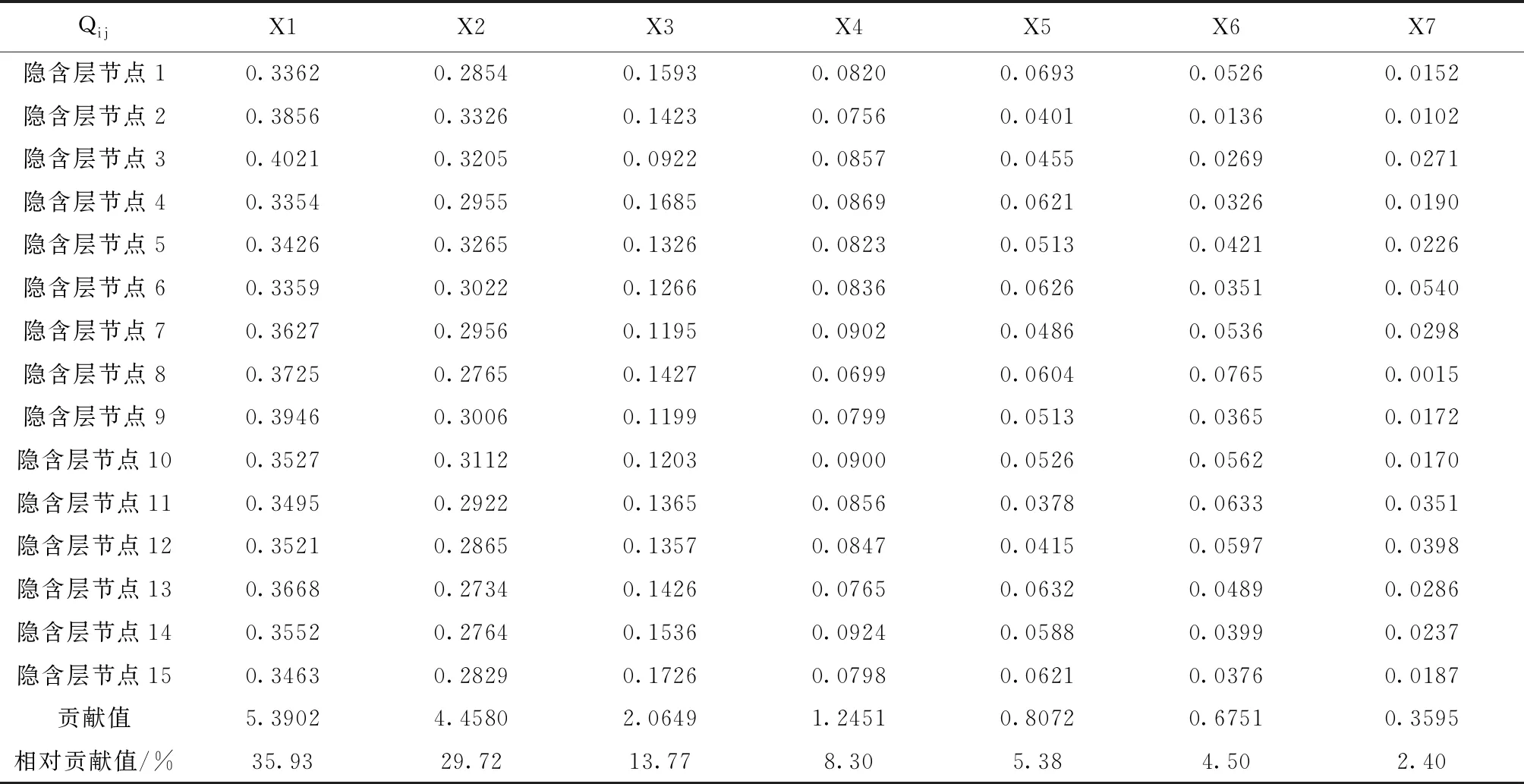
表3 各影响因素相对贡献程度
3 结 论
(1)选取7个因素作为影响堤岸稳定性的评价指标,采用神经网络与Garson算法组合模型对不同因素的敏感性进行分析,结果与实际工程较为符合,具有一定的可行性。
(2)文中研究边坡为均质边坡,对于复杂的多层边坡需要更多的工程实例作为验证,对该模型的适用性进行进一步改进。
(3)堤岸稳定性对于黏聚力和内摩擦角的变化最为敏感。
