降雨量随机特征分析与降雨预报研究

王雪玉

(黑龙江省大庆水文局，黑龙江 大庆 163000)

长期以来，为了得到确定性的输出数据，人们已经习惯了根据输入的资料来建立确定性的水文模型。但近几年来越来越多的水文研究工作者们尝试着突破传统的思维模式, 采用模糊数学、随机理论、贝叶斯理论等一系列新理论和新方法，积极探索和发现采用水文模型结构以及参数估计等方法所带来的不确定性, 并取得了许多研究成果[1-2]。本文基于建三江地区30 a的降雨量数据进行随机性分析。

1 不确定性方法分析降雨量

首先采用非线性拟合的方法，对建三江管局30 a月降雨量及年降雨量资料进行不确定分析[3-4]。分析过程中，使用MATLAB软件编程计算，由于月降雨量和年降雨量数据样本离散程度比较大，改为对样本进行概率密度图的拟合，以此来减弱影响性。对建三江管局全年实测数据概率分布与各月及年降雨量正态分布拟合函数参数如图1、表1所示。

图1 全年实测数据概率分布

表1 各月及年降雨量正态分布拟合函数参数

结果表明，以核密度估计辅助分析，拟合曲线符合正态分布函数。

2 年降雨量预报

自相关分析是研究水文序列内部线性相依性质的统计技术，是进行时间序列分析的有效方法，它简单易行、较为直观。利用自相关分析法可以测定时间序列的随机性和平稳性，以及时间序列的季节性。常用自相关系数和自相关图研究这种性质。

对实测数据使用AR自回归模型预报，并对该区域年降雨量进行预报。求出预测值相对误差，看是否在容许范围之内，是否可以作为预报值使用。若可以作为预报值使用，则将不确定性分析的成果应用在预报上，模拟出10次30 a周期的数据。再将模拟数据输入到自回归模型中运算，得出预测相对误差均值。

由于自回归模型方便计算，易于编程，所以采用MATLAB编程计算，计算结果准确且易于表达。首先观察实测数据的离散程度，将处理过后的数据进行自相关及偏相关分析。如图2和图3所示。

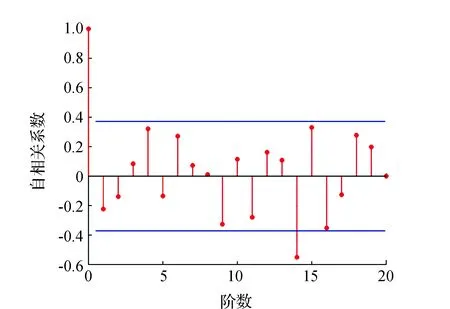
图2 自相关分析

图3 偏相关分析

由自相关分析图2可以看出“拖尾性”，满足置信区间的为4阶或其左右。但是不足以判断自相关阶数，从偏相关分析图3可以看出大致“截尾性”，判断阶数在4阶左右。但是无法确定出准确的阶数。需要对序列样本进行AIC法则检测。检测结果如表2所示。

AIC法则检测后，发现3阶的值才是最小的，所以可以定阶数为3。运行AR自相关模型程序进行样本的逼近拟合，并预报最后两年的年降雨量。如图4所示。

表2 AIC法则检验表

图4 AR(3)年降雨量计算结果过程线

经计算，2009年预测值为418.19 mm，实测值为572.70 mm，2010年预测值为556.67 mm，实测值为503.10 mm。两次预测值与实际值的相对误差为18.81%，小于20%。预测值在容许范围内，可以用来预报年降雨量。

3 基于模拟数据及参数优化预报

由于自回归模型是基于实测数据预报的，结果是确定性的，误差值一般比较高。为降低预报误差，基于之前对建三江月降雨量的不确定性分析，做出如下假设：以1981—2010年这30 a为1个周期，通过计算机模拟，模拟出10个周期的降雨量序列样本，也就是重现这30 a 10次，预报10次并综合分析预报结果。对每一年的每一个月取符合分布的10个随机数，再将12个月的随机数求和即为模拟年的年降雨量。这样，总共可以模拟出300 a的数据样本，也就是10个30 a周期。对这10个30 a重复进行AR自回归模型运算，将结果整理如表3、表4所示。

表3 模型预测数据

注：W为自回归方程的系数；at为白噪声；MAPE为平均绝对百分误差，%。

表4 各种情况下MAPE对比

10次模拟之后，平均绝对百分误差为18.34%，比实测数据降低了0.47个百分点。

通过10次模拟30 a周期，可以得到10组回归方程。也就是说，可以得到10组参数。考虑到除了样本数据的不确定性以外，参数也可能存在不确定性，所以对10组参数进行优化。排除2组2阶参数，在剩余8组参数中选择最优2组参数取均值。用优化过后的系数重新构建自回归方程并预测。

优化后预测出的平均绝对百分误差为17.99%，比实测数据降低了0.82个百分点。

4 结 论

本文对水文不确定性研究的主要方法和内容进行总结和比较。采用了非线性拟合技术对建三江月降雨量进行的随机分布进行了研究。利用自相关技术以及AR自回归模型对年降雨量时间序列的预报进行了研究。

(1)用非线性拟合对建三江月降雨量进行不确定性分析，得出30 a的各个月份降雨量概率密度服从正态函数分布。此外，通过核密度估计辅助拟合，发现内核函数为正态分布函数的核密度函数拟合效果最佳，服从正态分布。

(2)对实测数据使用AR自回归模型预报，预测值相对误差为18.81%，在容许范围之内，可以作为预报值使用。将不确定性分析的成果应用在预报上，模拟出10次30 a周期的数据。将模拟数据输入到自回归模型中运算，得出的预测相对误差均值为18.34%，误差缩小。考虑到除了样本数据不确定性对预测结果的影响，参数的不确定性也应该考虑。再通过对参数的优化，取2组误差最小的参数均值重新建立自回归模型预测，预测值相对误差减小至17.99%。

(3)通过增加模拟的次数可以将预报误差缩小，对参数的优化也可以将预报误差缩小。由此可以设想，通过计算机进行大量的重现期模拟可以将误差缩小到一个极限值，有待进一步研究。