基于应用背景的旋转体体积的教学设计

张莹 许勇 武海波

摘要：本文采用启发式和问题驱动式教学方法，从旋转体的构成方式入手，借助硬币旋转的实例探究，引出了旋转体的概念;随后继续利用“硬币”的形象化分析，建立了旋转体体积的求解方法，并将其应用到实际问题中。

关键词：高等数学;教学设计;旋转体体积

中图分类号：O13     文献标志码：A     文章编号：1674-9324（2019）20-0050-02

《高等数学》是高等院校理工类各专业的公共基础课，其因较强的逻辑性、抽象性、应用性，有利于训练学生的抽象思维、逻辑思维和解决实际问题的能力，是开展素质教育、培养学生创新精神和创新能力的重要课程[1]。定积分应用中的微元法精妙地体现了“化整为零、积零为整”的思想，它对于微积分的学习和理解具有重要的理论价值和实际意义。但是学生在学习用微元法解决旋转体体积计算问题时，通常对旋转体的空间构成理解不够深入，在微元的选择上容易与后续学习的柱壳法相混淆。因此，本设计采用启发式和问题驱动式教学方法[2-3]，在形象化展示抽象数学概念的基础上，提出问题、引起兴趣、引发思考，最终实现知识的正确掌握与方法的深入理解，并将其应用到实际中去。

一、教学设计思路

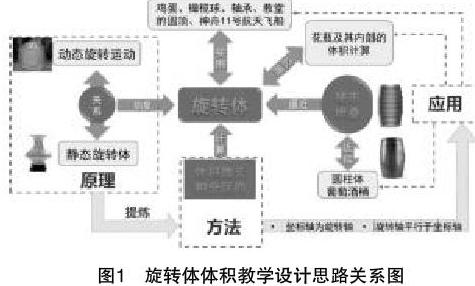
本设计从芭蕾舞演员和旋转木马的动态旋转，以及花瓶、鸡蛋、橄榄球和航天器的旋转结构入手，提出动态旋转和静态旋转结构之间的关系问题[4]。进而，通过分析硬币旋转构成球体的小游戏，将“动”与“静”相结合，引入旋转体的概念。随后，继续利用硬币堆叠来逼近圆柱体体积，并将其推广到更一般的旋转体体积逼近与求解问题中，引出微元法的思想，进一步运用定积分建立求解旋转体体积的积分公式，并用其求解典型旋转体的体积。最后，利用该求解方法，计算花瓶及其内部体积。教学设计思路关系如图1所示。

二、教学过程

1.概念的引入。首先，提出花瓶及其内部体积如何计算的问题;随后，展示冰上芭蕾和旋转木马的运动视频，以及自然界和人类社会中存在的多种静态旋转结构，如鸡蛋、灯笼、陶艺作品、教堂的圆顶。通过“动”与“静”的对比，引出本节的研究对象及学习内容。进一步引导学生观察旋转硬币的过程，探讨“动”与“静”的关系，发现二维图形旋转构成三维立体的逻辑关系，继而给出旋转体的定义，即由一个平面图形绕所在平面内一条定直线旋转一周而成的立体，这条直线称为旋转軸。

2.旋转体体积的计算。明确了旋转体的定义后，又该如何根据其构成特点，寻找求解旋转体体积的方法呢？圆柱作为最基本的旋转体，可以借助半径相同硬币的堆叠来进行逼近，即计算每个硬币的体积，再相加即可获得圆柱体的体积。对于更一般的情形，如葡萄酒桶的体积问题，引导学生分析圆柱体与葡萄酒桶体积问题的异同，提出问题启发思考，即是否也可通过硬币的累加来逼近葡萄酒桶的体积呢？不难发现这正是微元法的核心思想，通过细分、近似得到微元，就可以进一步利用定积分来求得葡萄酒桶的体积，如图2所示。这一个个堆叠的硬币就是体现了体积微元的选择，可见体积微元的选择与计算都与旋转轴的方向与位置有着密切的联系。因此，关于旋转体体积的计算可以根据旋转轴和微元的关系分为两大类来讨论。

在掌握了两类情形下旋转体体积的计算方法后，课程中将通过例题展示不同情形的问题，在与学生互动交流中，检验学生对概念的理解和对方法的掌握程度。如：例1，计算由抛物线弧x=y2，y∈[0，1]与x轴、直线x=1围成的图形分别绕y轴和x轴旋转一周所成旋转体的体积;例2，求由曲线y=4-x2及y=0所围成的图形绕直线x=3旋转所构成的旋转体的体积。

3.实际应用。至此，我们已经掌握了旋转体体积求解的基本思路和方法。课程开始时提到的鸡蛋和橄榄球等实际问题的体积如何求解呢？不妨以花瓶为例，想要求得花瓶及其内部的整体体积，可分为五步：（1）建立恰当的直角坐标系;（2）拟合平面曲线;（3）确定旋转轴及积分变量和区间;（4）确定半径函数并写出积分式;（5）求解定积分得到体积。这样，就可以通过建模的思想，借助本节课所学概念和方法实现实际问题的求解。

本节内容是训练使用微元法的重要载体，对培养学生的数学建模能力、逻辑思维能力和抽象思维能力非常重要。通过硬币的引入，使学生对问题的求解形成深刻且直观的印象。在学习过程中，虽然会根据旋转轴不同，分为多种情景进行研究，但问题的核心不变，即把握微元法思想，明确微元选取方向与旋转轴的关系，通过确定积分微元和积分区间，即可求得旋转体的体积。在分析抽象数学问题的基础上，进一步分析花瓶及其内部体积求解的实际问题，培养了学生利用微积分知识分析实际问题的能力。

参考文献：

[1]西北工业大学高等数学教材编写组.高等数学：下册[M].第3版.北京：科学出版社，2013：50-57.

[2]郑淑芬.案例教学法的作用、实施环节及需要注意的问题[J].教育探索，2008，3（4）：56-57.

[3]陶沼灵.启发式教学方法研究综述[J].中国成人教育，2007，（7）：139-140.

[4]郜舒竹，徐春华.对旋转体体积的再认知[J].数学通报，2005，44（1）：54-57.